這門課和另一門課內容都差不多，可以參考七、決策樹算法和集成算法該篇博文。

一、決策樹相關概念

邏輯回歸本質

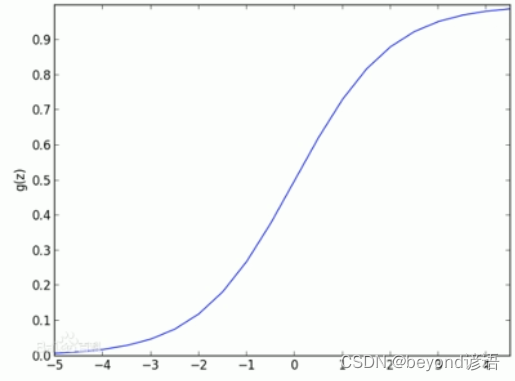
邏輯回歸：線性有監督分類模型。常用求解二分類問題，要么是A類別要么是B類別，一般會以0.5作為劃分閾值，因為一般邏輯回歸的激活函數使用的是sigmoid函數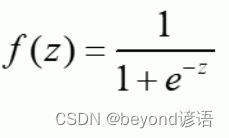
例如：一條數據中有六個特征


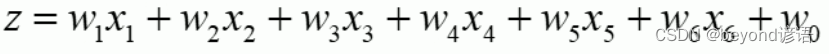
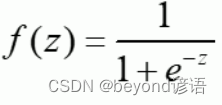
邏輯回歸會將0.5作為劃分的閾值，例如：

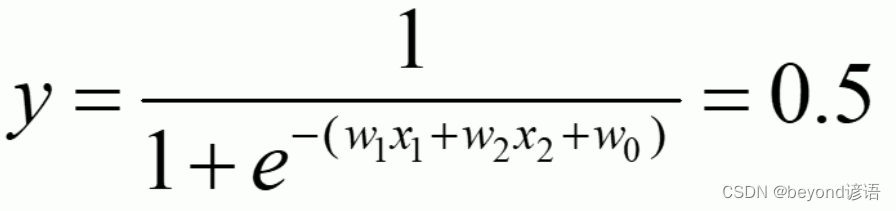
化簡可得：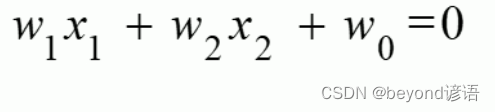
其實這也就找到了一條分界線，這里只考慮兩個維度，x1和x2。

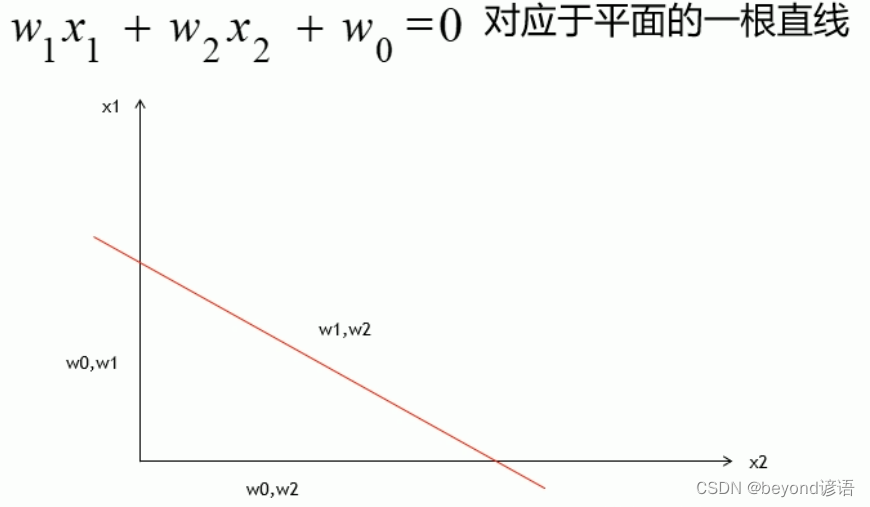
邏輯回歸的本質就是靠這條直線來對數據進行劃分成多個類別
例如：通過邏輯回歸進行二分類任務，數據是由兩個維度組成(x1,x2)，y為類別號，這里是二分類只有0,1兩個類別：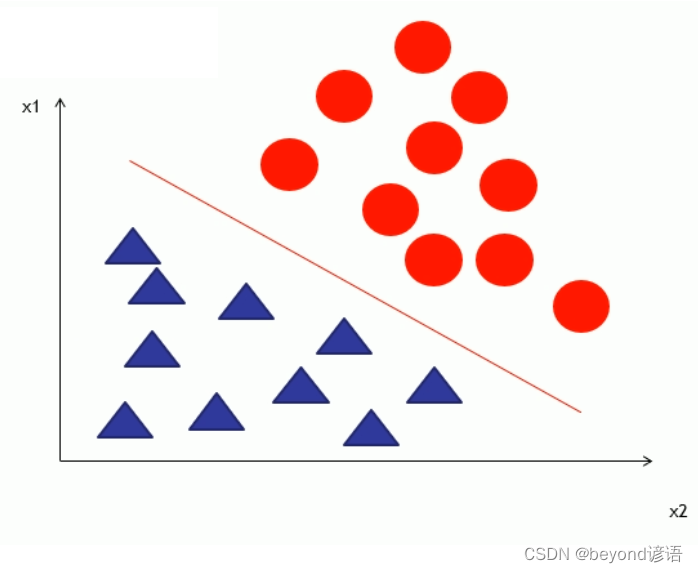
邏輯回歸的本質就是找到這樣的一條直線對已有的數據點進行劃分。未來有新的點落到這個圖中的時候，只要知道(x1,x2)，就可以進行預測是0還是1，也就是是紅圓還是藍三角。
因為是找到一條直線進行分割，故是線性的
因為樣本中需要含有標簽y的值，故是有監督的
因為最終可以將不同的數據進行劃分了兩類，故是分類的

決策樹本質

決策樹：非線性有監督分類模型。

擬合：多元線性回歸
分類：邏輯回歸(線性的)

為了使得這些線性的模型去擬合那些非線性的數據，一般使用Polynomial多項式回歸，對data數據進行轉換，把非線性的數據轉換為線性的數據，這樣就可以使用線性的模型去擬合線性的數據。

二、決策樹案例分析

決策樹必須要求數據離散化
例如：數據信息包括性別、天氣、是否有風等，就得把男1女0進行分開、晴天0多云1雨天2等分開、有風1無風0分開

Ⅰ，數據如何進行離散化

1，離散數據

動物：貓、狗、豬，如何離散化？把貓標記為0，狗為1，豬為2？倆狗等于豬？是不是多少有點不合適，這時候引入了one-hot編碼，通俗一點就是貓001，狗010，豬100，沒有誰大誰小區分。
離散數據還需要指明數量2^M種分割方式，M為數據的維度，也就是有幾類。
這里有3個維度類別，故有2^3=8種分割方式

2，連續數據

成績：不及格[0-60)、良好[60-90)、優秀[90-100]
連續數據也需要指明數量M+1種分割方式，M為數據的維度，也就是有幾類。
這里有3個維度類別，故有4種分割方式

Ⅱ，為啥要進行離散化

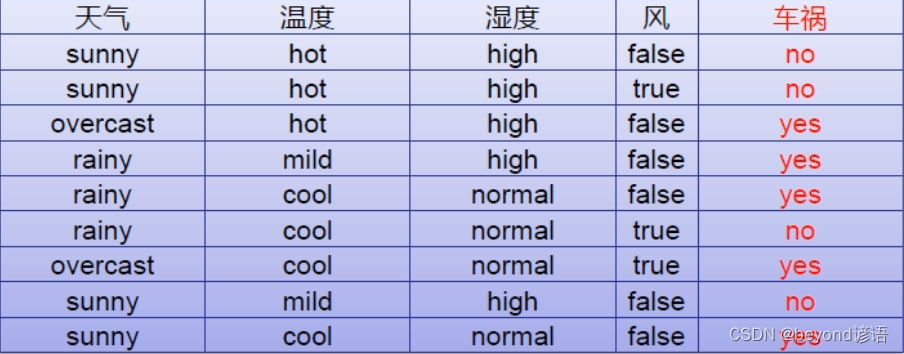
將數據集中的數據進行離散化之后就可以很好的進行構建樹了，有數據訓練出樹(模型)，最終預測是否會發生車禍
決策樹是通過固定的條件來對類別進行判斷

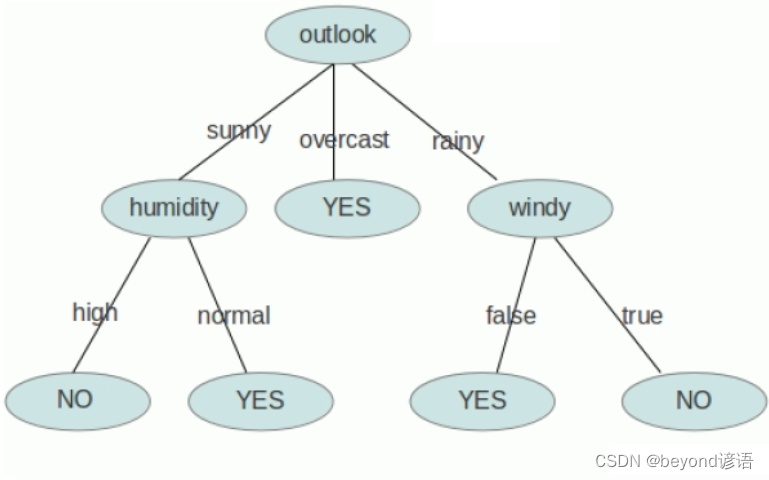
Ⅲ，決策樹的生成

數據不斷的分類遞歸的過程，每一次的分裂，盡可能讓類別一樣的數據放在樹的一邊，當樹的葉子節點的數據都是一類的時候，就停止分類。

Ⅳ，決策樹的評判標準

上面樣本中，天氣、溫度、濕度、風，這些因素都會導致車禍的發生，但是在進行決策樹分類的時候，分成幾類？先從哪進行劃分？這就成了一個問題，也就是哪個因素是引起車禍的主要原因這一點需要思考，評判。
決策樹會將所有的因素排列組合都進行代入運算，然后將所分割的結果進行標準評分，求出所有的結果然后取最優解
決策樹的主旨就是盡可能的將一類分到一邊，何為一類？這就需要一個標準，下面為三個主要的標準，也是較為常用的指標

第一個是基尼系數，這個概念來源于經濟學，也就是貧富差距，數越大，貧富差距越大，越不是一類。
第二個是熵，熵是衡量數據不確定性
第三個是方差，方差很簡單，就是看這些數據是否差不多
前兩個常用于分類任務，最后一個常用于回歸任務

三、決策樹的缺點及解決方法

缺點：①運算量大，需要一次加載所有的數據進入內存，并且尋找分割條件，這是一個極耗資源的過程。
②訓練樣本中出現異常的數據時，會對決策樹產生很大的影響，決策樹的抗干擾能力很差。因為需要加載所有的數據，對數據的準確性很是依賴，故導致抗干擾能力很差。

邏輯回歸的抗干擾能力很強，其如何抗干擾，也就是線性回歸的抗干擾能力如何體現？
答：通過L1和L2正則，利用懲罰性來進行增強模型的泛化能力。L1、L2正則

其實在面對線性不可分的情況下，主要有兩種處理辦法：
①升維，若在二維平面線性不可分可以通過升維(第三個維度一般為x1*x2)，到三維空間之后就可以很容易通過一個平面來將數據進行分割劃分
②使用非線性模型來處理，比如決策樹、隨機森林等

邏輯回歸可以得出一個0-1之間的概率值，人為可以設置一個閾值例如0.5，來進行分類；而決策樹只能得出一個分類號0或1

解決方法：①減少決策樹所需訓練的樣本數（訓練模型本來就需要大量的數據，你這一來數據量少了，模型相對來說并不會太準確）
②隨機采樣，降低異常數據的干擾（得靠運氣，萬一隨機采樣都是干擾點傻臉了）
這時候需要用到隨機森林了

四、代碼實現

import pandas as pd
import numpy as np
from sklearn.datasets import load_iris#導入鳶尾花數據集
from sklearn.tree import DecisionTreeClassifier#用決策樹做分類
from sklearn.tree import export_graphviz
from sklearn.tree import DecisionTreeRegressor#用決策樹做回歸
from sklearn.model_selection import train_test_split#將數據集進行設置訓練集和測試集的比例
from sklearn.metrics import accuracy_score#評估分類的準確率
import matplotlib.pyplot as plt#可視化圖像
import matplotlib as mpliris = load_iris()#導入鳶尾花數據集
data = pd.DataFrame(iris.data)#將數據集轉換為DataFrame格式
data.columns = iris.feature_names#往數據中加載特征名，也就是花萼的長寬、花瓣的長寬等特征
data['Species'] = load_iris().target#對數據集的結果y起個名稱
# print(data)x = data.iloc[:, :2]  # 花萼長度和寬度
y = data.iloc[:, -1]
# y = pd.Categorical(data[4]).codes
# print(x)
# print(y)x_train, x_test, y_train, y_test = train_test_split(x, y, train_size=0.75, random_state=42)#將數據集進行劃分tree_clf = DecisionTreeClassifier(max_depth=8, criterion='entropy')#設置決策樹的深度8；使用entropy熵進行評判
tree_clf.fit(x_train, y_train)
y_test_hat = tree_clf.predict(x_test)
print("acc score:", accuracy_score(y_test, y_test_hat))"""
export_graphviz(tree_clf,out_file="./iris_tree.dot",feature_names=iris.feature_names[:2],class_names=iris.target_names,rounded=True,filled=True
)# ./dot -Tpng ~/PycharmProjects/mlstudy/bjsxt/iris_tree.dot -o ~/PycharmProjects/mlstudy/bjsxt/iris_tree.png
"""print(tree_clf.predict_proba([[5, 1.5]]))#指定 花萼長度、寬度 來進行預測
print(tree_clf.predict([[5, 1.5]]))#返回最終的分類號depth = np.arange(1, 15)
err_list = []
for d in depth:clf = DecisionTreeClassifier(criterion='entropy', max_depth=d)#深度從1-15依次進行遍歷clf.fit(x_train, y_train)y_test_hat = clf.predict(x_test)result = (y_test_hat == y_test)if d == 1:print(result)err = 1 - np.mean(result)print(100 * err)err_list.append(err)print(d, 'error rate:%.2f%%' % (100 * err))mpl.rcParams['font.sans-serif'] = ['SimHei']#設置字體為SimHei
plt.figure(facecolor='w')#圖的底色為白色
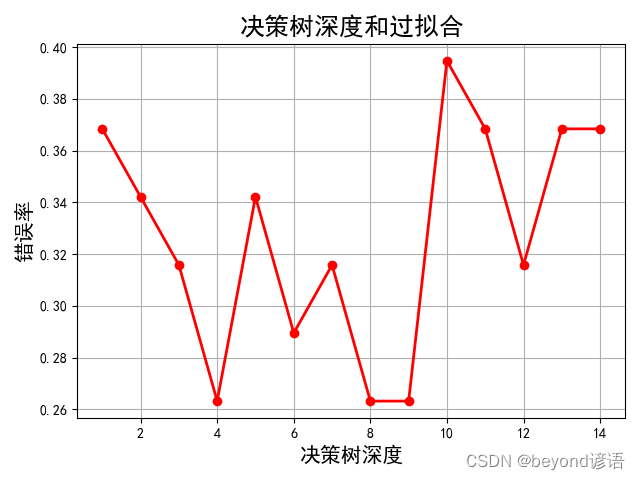
plt.plot(depth, err_list, 'ro-', lw=2)#橫坐標為樹的深度，縱坐標為錯誤率
plt.xlabel('決策樹深度', fontsize=15)
plt.ylabel('錯誤率', fontsize=15)
plt.title('決策樹深度和過擬合', fontsize=18)
plt.grid(True)
plt.show()# tree_reg = DecisionTreeRegressor(max_depth=2)
# tree_reg.fit(X, y)

"""
acc score: 0.7368421052631579
[[0. 1. 0.]]
[1]
73     False
18     False
118     True
78     False
76     False
31      True
64     False
141     True
68     False
82     False
110     True
12      True
36     False
9       True
19      True
56     False
104     True
69     False
55     False
132     True
29      True
127     True
26      True
128     True
131     True
145     True
108     True
143     True
45      True
30      True
22      True
15     False
65     False
11      True
42      True
146     True
51     False
27      True
Name: Species, dtype: bool
36.8421052631579
1 error rate:36.84%
34.210526315789465
2 error rate:34.21%
31.57894736842105
3 error rate:31.58%
26.315789473684216
4 error rate:26.32%
34.210526315789465
5 error rate:34.21%
28.947368421052634
6 error rate:28.95%
31.57894736842105
7 error rate:31.58%
26.315789473684216
8 error rate:26.32%
26.315789473684216
9 error rate:26.32%
39.473684210526315
10 error rate:39.47%
36.8421052631579
11 error rate:36.84%
31.57894736842105
12 error rate:31.58%
36.8421052631579
13 error rate:36.84%
36.8421052631579
14 error rate:36.84%Process finished with exit code 0"""

五、隨機森林

決策樹不行，那就多來點，三個臭皮匠頂個諸葛亮，來個隨機森林
森林：多棵決策樹
隨機：生成樹的數據都是從數據加粗樣式集中隨機進行選取的
并行思路

Ⅰ隨機森林相關概念

一個大的決策樹的建立需要一個很大的服務器去支撐，但是若分成多個小的決策樹呢？每棵樹都互不影響，可以并行執行，這就體現了分布式的優勢所在了。
決策樹可以看成一個人，森林可以看成多個人，你去問路，2個人給你說路口左轉，8個人給你說路口右轉，你到路口之后你會左轉還是右轉？正常人都會右轉，你要是頭鐵非得左轉也行。
即使有的樹出問題了受到干擾點的影響了，但絕大多數的決策樹還正常最終仍然可以得到正確的結果，這就是集體智慧的真實寫照

Ⅱ隨機森林優點

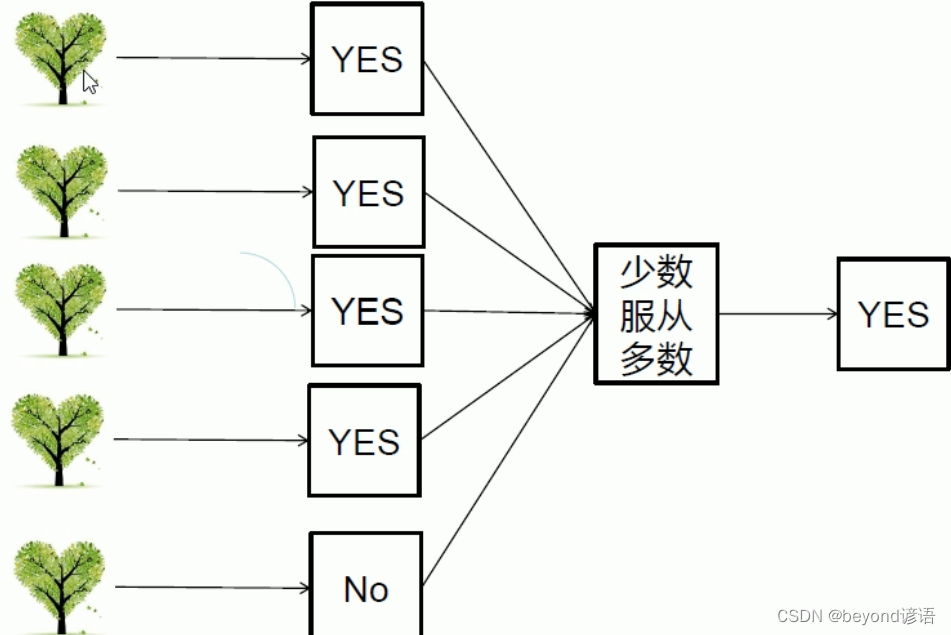
①當數據集很大的時候，可以隨機選取數據集的一部分，生產一棵樹，重復這些過程，可以生成多棵互不相同的樹，這些樹擱一塊就形成了森林。

②對每一棵樹都進行判斷，得到的結果少數服從多數，最終確定出正確的結果

Ⅳ邏輯回歸和隨機森林對比

邏輯回歸	隨機森林
軟分類	硬分類
線性模型	非線性模型
輸出為概率值，有實際意義	輸出為樣本號，無實際意義
抗干擾能力強	抗干擾能力弱

對于邏輯回歸的軟分類：之所以是軟分類是因為閾值可以改變
比如：①Ａ得癌癥了，但是誤判沒得、②Ｂ沒得癌癥，但是誤判得了。
你覺得哪個更難受？應該是①，因為②的話是虛驚一場，而①是蒙蔽雙眼
所以有必要為了避免①的誤判情況的發生，應該相應的修改閾值。因為可以修改閾值，故分類情況也在隨時的發生改變，因此成為軟分類

隨機森林中的每一棵決策樹的數據都是隨機來源于數據集中的數據，若需要提高純度，就需要葉子節點個數很多，才能保證每個類別的純度特別純，極端情況下會將每個數據都單獨分為一類，每個葉子節點是一類，純度百分百，但是分的過于細碎也不是好事，會產生過擬合！！！訓練集的數據分的很好，每個都是一類，但是未來做預測的時候，拿到新數據的時候就傻臉了。

隨機森林出現了多個葉子節點，分類純度很高，但會出現過擬合，此時就需要就行剪枝來避免過擬合現象。

六、代碼實現

from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split#隨機森林分類器
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
from sklearn.datasets import load_irisiris = load_iris()#導入鳶尾花數據集
X = iris.data[:, :2]  # 花萼長度和寬度，取其他特征也行
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)#設置訓練集和測試集的比例rnd_clf = RandomForestClassifier(n_estimators=15, max_leaf_nodes=16, n_jobs=1)#隨機森林分類器；n_estimators 500棵小決策樹構成森林
rnd_clf.fit(X_train, y_train)#rnd_clf和bag_clf是等價的，用誰都可以，都是在創建隨機森林
bag_clf = BaggingClassifier(DecisionTreeClassifier(splitter="random", max_leaf_nodes=16),n_estimators=15, max_samples=1.0, bootstrap=True, n_jobs=1
)#Bagging是一個思想，一個并行運算處理的思想
bag_clf.fit(X_train, y_train)y_pred_rf = rnd_clf.predict(X_test)
y_pred_bag = bag_clf.predict(X_test)
print(accuracy_score(y_test, y_pred_rf))
print(accuracy_score(y_test, y_pred_bag))# Feature Importance 特征的重要性
iris = load_iris()
rnd_clf = RandomForestClassifier(n_estimators=500, n_jobs=-1)
rnd_clf.fit(iris["data"], iris['target'])
for name, score in zip(iris['feature_names'], rnd_clf.feature_importances_):print(name, score)

七、提取重要特征的常用方法

①Pearson相關性來找重要的特征
②正則，例如Lasso Regression、Ridge Regression（嶺回歸）等
③樹

八、剪枝

所謂的剪枝就是將隨機森林或者決策樹的一些分支進行裁剪，防止過擬合現象的出現。

Ⅰ預剪枝

當樹還沒有長成的時候，也就是模型還沒訓練好的時候，或者是還沒有分裂的時候提前設置一些條件，當分裂到這種情況的時候，就不再分裂了。
樹的模型也就這樣了，已經規定好了
預剪枝常用，當模型進行構建封裝的時候，需要用戶提供一些超參數，這些超參數就是用來控制樹的規模，從而達到預剪枝的目的和效果

Ⅱ預剪枝方式

①可以設置層次，即控制分裂的層數，例如最多只能分裂兩層，到了兩層就不會再分了
②可以控制樣本數量，即每個節點包含的樣本個數。例如設定樣本個數為5，有8個樣本在上一個節點里，大于規定的樣本數量5，需要分裂，假如分成4和4，這兩個節點的樣本個數小于5，故不會再進行分裂了

Ⅲ后剪枝

隨便分裂吧，分裂完之后，或者說模型訓練完成之后，再人為的將一些細枝末節的地方進行去掉
這就需要模型算法師來進行優化處理，比如有的節點可以合并，那就進行合并，將倆葉子節點合并成一個

九、Bagging

from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import VotingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score#創建三個獨立的分類模型
log_clf = LogisticRegression()
rnd_clf = RandomForestClassifier()
svm_clf = SVC()
#投票分類器，硬分類，少數服從多數
voting_clf = VotingClassifier(estimators=[('lr', log_clf), ('rf', rnd_clf), ('svc', svm_clf)],voting='hard'
)iris = load_iris()
X = iris.data[:, :2]  # 花萼長度和寬度
y = iris.target
# X, y = make_moons()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)voting_clf.fit(X, y)for clf in (log_clf, rnd_clf, svm_clf, voting_clf):clf.fit(X_train, y_train)y_pred = clf.predict(X_test)print(clf.__class__.__name__, accuracy_score(y_test, y_pred))bag_clf = BaggingClassifier(DecisionTreeClassifier(), n_estimators=500,max_samples=1.0, bootstrap=True, n_jobs=1
)
bag_clf.fit(X_train, y_train)
y_pred = bag_clf.predict(X_test)
print(y_pred)
y_pred_proba = bag_clf.predict_proba(X_test)
print(y_pred_proba)
print(accuracy_score(y_test, y_pred))# oob
bag_clf = BaggingClassifier(DecisionTreeClassifier(), n_estimators=500,bootstrap=True, n_jobs=1, oob_score=True
)
bag_clf.fit(X_train, y_train)
print(bag_clf.oob_score_)
y_pred = bag_clf.predict(X_test)
print(accuracy_score(y_test, y_pred))print(bag_clf.oob_decision_function_)

"""
LogisticRegression 0.82
RandomForestClassifier 0.76
SVC 0.78
VotingClassifier 0.8
[1 0 2 1 1 0 1 2 1 1 2 0 1 0 0 2 2 1 1 2 0 1 0 2 2 1 1 2 0 0 0 0 2 0 0 1 20 0 0 1 2 2 0 0 1 2 2 2 2]
[[0.         0.8205     0.1795    ][0.718      0.213      0.069     ][0.         0.224      0.776     ][0.         0.58936667 0.41063333][0.         0.53300476 0.46699524][0.806      0.178      0.016     ][0.002      0.92333333 0.07466667][0.         0.46225714 0.53774286][0.         0.65855238 0.34144762][0.         0.50667619 0.49332381][0.         0.074      0.926     ][0.956      0.012      0.032     ][0.438      0.484      0.078     ][0.994      0.002      0.004     ][1.         0.         0.        ][0.002      0.01       0.988     ][0.         0.114      0.886     ][0.         0.654      0.346     ][0.         0.77733333 0.22266667][0.         0.404      0.596     ][1.         0.         0.        ][0.         0.76036667 0.23963333][1.         0.         0.        ][0.         0.404      0.596     ][0.04       0.02933333 0.93066667][0.         0.6612     0.3388    ][0.         0.8012     0.1988    ][0.         0.11613333 0.88386667][0.956      0.012      0.032     ][0.994      0.002      0.004     ][1.         0.         0.        ][0.756      0.195      0.049     ][0.         0.22566667 0.77433333][1.         0.         0.        ][1.         0.         0.        ][0.         0.8        0.2       ][0.         0.072      0.928     ][0.982      0.01       0.008     ][1.         0.         0.        ][0.998      0.002      0.        ][0.         0.50667619 0.49332381][0.12       0.2925     0.5875    ][0.         0.22566667 0.77433333][0.982      0.018      0.        ][0.974      0.02       0.006     ][0.         0.976      0.024     ][0.         0.15       0.85      ][0.         0.10003333 0.89996667][0.         0.31       0.69      ][0.008      0.03533333 0.95666667]]
0.76
0.64
0.76
[[0.         0.96039604 0.03960396][0.         0.00512821 0.99487179][0.02083333 0.82621528 0.15295139][1.         0.         0.        ][0.         0.06748466 0.93251534][0.         0.23735955 0.76264045][0.92063492 0.07407407 0.00529101][1.         0.         0.        ][1.         0.         0.        ][0.07853403 0.84816754 0.07329843][0.         0.27387387 0.72612613][1.         0.         0.        ][0.7797619  0.19642857 0.02380952][0.99386503 0.00613497 0.        ][0.         0.51217617 0.48782383][1.         0.         0.        ][0.01005025 0.91139028 0.07855946][0.12365591 0.05734767 0.81899642][1.         0.         0.        ][0.         0.34530387 0.65469613][0.         0.98972973 0.01027027][0.51912568 0.38251366 0.09836066][0.         0.62020202 0.37979798][0.         0.84375    0.15625   ][0.         0.19949495 0.80050505][0.87878788 0.12121212 0.        ][0.01657459 0.3038674  0.67955801][0.01197605 0.9251497  0.06287425][0.92432432 0.07567568 0.        ][0.11627907 0.79651163 0.0872093 ][0.         0.46180556 0.53819444][0.99468085 0.00531915 0.        ][0.9673913  0.0326087  0.        ][0.         0.94252874 0.05747126][0.         0.04972376 0.95027624][0.98979592 0.         0.01020408][0.         0.64481715 0.35518285][1.         0.         0.        ][1.         0.         0.        ][0.07692308 0.33717949 0.58589744][0.03592814 0.7005988  0.26347305][0.         0.5469428  0.4530572 ][0.         0.39035088 0.60964912][0.         0.94313725 0.05686275][0.         0.00625    0.99375   ][0.         0.87640449 0.12359551][0.99404762 0.00595238 0.        ][0.99470899 0.00529101 0.        ][0.         0.86612022 0.13387978][0.         0.15008726 0.84991274][1.         0.         0.        ][1.         0.         0.        ][0.99375    0.00625    0.        ][0.         0.46486486 0.53513514][0.00606061 0.02424242 0.96969697][1.         0.         0.        ][0.         0.68693694 0.31306306][0.00515464 0.06701031 0.92783505][1.         0.         0.        ][0.         0.88557214 0.11442786][0.         0.16315789 0.83684211][0.         0.76439791 0.23560209][0.         0.08242972 0.91757028][0.         0.22894737 0.77105263][1.         0.         0.        ][0.         0.65789474 0.34210526][0.00549451 0.2032967  0.79120879][0.         0.30319149 0.69680851][0.         0.5923913  0.4076087 ][0.07368421 0.77368421 0.15263158][0.         0.38802682 0.61197318][0.07185629 0.71257485 0.21556886][0.         0.57954545 0.42045455][0.         0.97826087 0.02173913][0.96039604 0.02970297 0.00990099][0.02298851 0.80823755 0.16877395][0.         0.1878453  0.8121547 ][0.00564972 0.05649718 0.93785311][1.         0.         0.        ][0.04060914 0.30964467 0.64974619][0.00540541 0.05405405 0.94054054][0.         0.02260638 0.97739362][1.         0.         0.        ][0.         0.60706349 0.39293651][0.88268156 0.04469274 0.0726257 ][0.         0.02857143 0.97142857][0.         0.05472637 0.94527363][0.         0.82285714 0.17714286][0.         0.37244898 0.62755102][0.         0.285      0.715     ][0.         0.56686391 0.43313609][0.         0.1761658  0.8238342 ][0.         0.96756757 0.03243243][0.00558659 0.89385475 0.10055866][0.50520833 0.45833333 0.03645833][0.         0.36190476 0.63809524][0.04651163 0.95348837 0.        ][0.26203209 0.34848485 0.38948307][0.         0.42791136 0.57208864][0.         0.53856383 0.46143617]]Process finished with exit code 0
"""

十、決策樹回歸

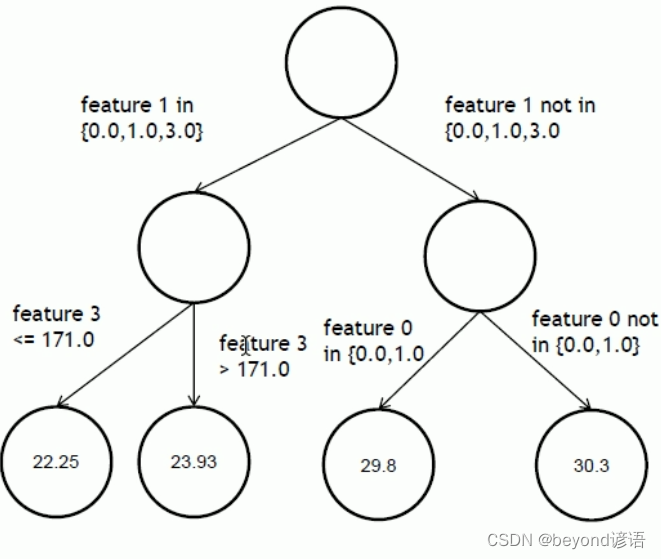
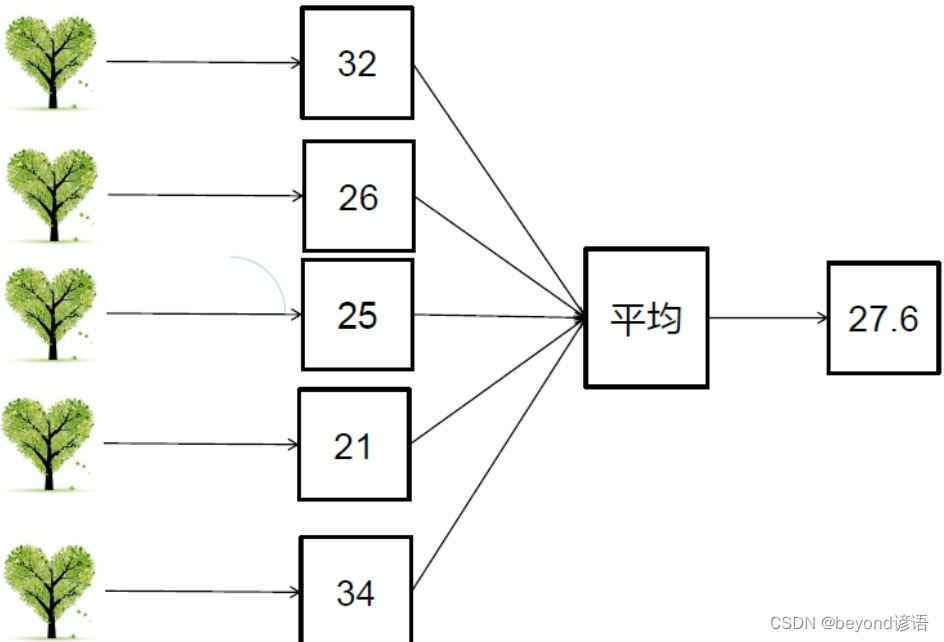
決策樹做分類就是將一個大的數據集分到多個小的葉子節點中去，例如，第一個特征在某個集合里面走左邊，反之走右邊。最后得到的數據的預測值是多少取決于最終葉子節點中的數值的平均值。

import numpy as np
from sklearn.tree import DecisionTreeRegressor
import matplotlib.pyplot as pltN = 100
x = np.random.rand(N) * 6 - 3
x.sort()y = np.sin(x) + np.random.rand(N) * 0.05#非線性變換 數據
print(y)x = x.reshape(-1, 1)
print(x)dt_reg = DecisionTreeRegressor(criterion='mse', max_depth=3)
dt_reg.fit(x, y)x_test = np.linspace(-3, 3, 50).reshape(-1, 1)
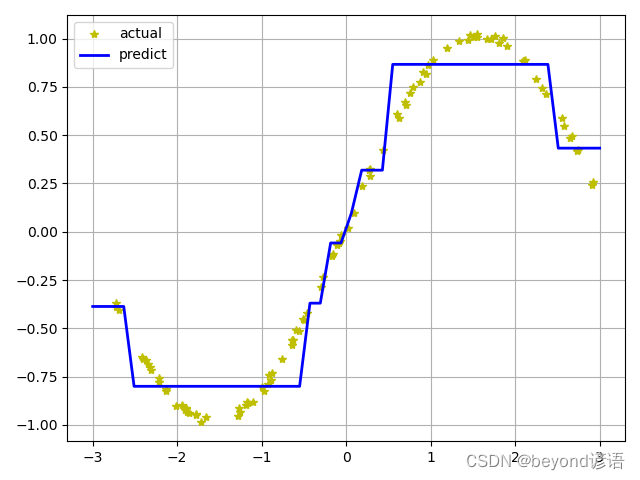
y_hat = dt_reg.predict(x_test)plt.plot(x, y, "y*", label="actual")
plt.plot(x_test, y_hat, "b-", linewidth=2, label="predict")
plt.legend(loc="upper left")
plt.grid()
plt.show()
# plt.savefig("./temp_decision_tree_regressor")# 比較不同深度的決策樹
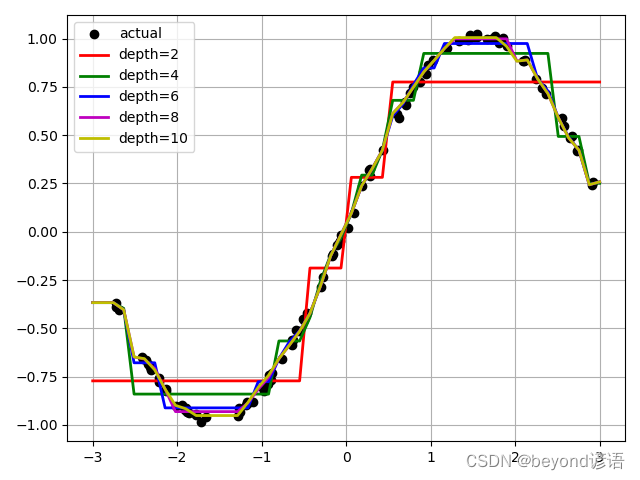
depth = [2, 4, 6, 8, 10]
color = 'rgbmy'
dt_reg = DecisionTreeRegressor()
plt.plot(x, y, "ko", label="actual")
x_test = np.linspace(-3, 3, 50).reshape(-1, 1)
for d, c in zip(depth, color):dt_reg.set_params(max_depth=d)dt_reg.fit(x, y)y_hat = dt_reg.predict(x_test)plt.plot(x_test, y_hat, '-', color=c, linewidth=2, label="depth=%d" % d)
plt.legend(loc="upper left")
plt.grid(b=True)
plt.show()
# plt.savefig("./temp_compare_decision_tree_depth")
"""
[-0.36688907 -0.38930987 -0.40414606 -0.64806473 -0.65700912 -0.66248474-0.6856528  -0.70139657 -0.71546988 -0.75949983 -0.77920805 -0.81452329-0.8222279  -0.90006776 -0.89734011 -0.92172404 -0.91383193 -0.91458672-0.91591471 -0.9307151  -0.93799345 -0.94902737 -0.94300522 -0.98441068-0.95912561 -0.95615789 -0.9101952  -0.93302889 -0.89679762 -0.88337589-0.88442261 -0.87954674 -0.80543953 -0.82610002 -0.78694966 -0.74295972-0.76677754 -0.72940886 -0.65740021 -0.58807926 -0.55983806 -0.56213145-0.50970546 -0.51535249 -0.45167804 -0.45721702 -0.42209345 -0.28375276-0.23336102 -0.12528549 -0.11341364 -0.06689013 -0.05751791 -0.04824017-0.01469778  0.02023206  0.09562457  0.23818302  0.32036025  0.28848320.32562788  0.42195215  0.61216689  0.58675132  0.66988573  0.654063280.71793552  0.74871883  0.77367746  0.82723622  0.81557531  0.862337530.88691045  0.94898301  0.98565776  0.99451228  1.01955382  1.008021021.00705746  1.02191846  0.99818839  1.0003569   1.01273956  0.976496391.00220468  0.9603402   0.88287074  0.88583015  0.88975818  0.792138840.7423791   0.71526646  0.59134944  0.5462042   0.48648846  0.494622380.42007109  0.4222635   0.24311189  0.25878365]
[[-2.72466555][-2.72226087][-2.68403246][-2.41254902][-2.39949207][-2.37147302][-2.34611684][-2.32081955][-2.31562513][-2.21292638][-2.21050926][-2.136452  ][-2.13037238][-2.01353511][-1.94177567][-1.91198378][-1.90590259][-1.8960628 ][-1.89140935][-1.87843641][-1.8589764 ][-1.78054242][-1.7792699 ][-1.72188473][-1.66002114][-1.28581879][-1.26540192][-1.2538425 ][-1.17999472][-1.17149249][-1.16311153][-1.1084779 ][-0.99671069][-0.97261305][-0.9253839 ][-0.91136908][-0.8857756 ][-0.8737135 ][-0.75420415][-0.64099704][-0.63742495][-0.63205098][-0.59173631][-0.56030877][-0.5152529 ][-0.50230676][-0.46816639][-0.29276163][-0.27334957][-0.1654072 ][-0.15476441][-0.10714786][-0.08879741][-0.07772982][-0.06149313][ 0.02008246][ 0.09340283][ 0.19048042][ 0.2754616 ][ 0.27809472][ 0.28520137][ 0.43450279][ 0.60262783][ 0.62416658][ 0.69830847][ 0.70433814][ 0.75158421][ 0.79467865][ 0.87619365][ 0.90570908][ 0.93894204][ 0.97296551][ 1.02672438][ 1.18810392][ 1.33863358][ 1.44490161][ 1.46442844][ 1.51606029][ 1.54505571][ 1.54514861][ 1.67111482][ 1.71420404][ 1.75846431][ 1.80892824][ 1.85273944][ 1.89965423][ 2.09460961][ 2.10921317][ 2.12111166][ 2.25236567][ 2.31865023][ 2.36767786][ 2.55649574][ 2.58114792][ 2.65451688][ 2.67623079][ 2.72668498][ 2.73827709][ 2.90997157][ 2.91823426]]
"""

十一、隨機森林回歸