題目

給定一個可包含重復數字的序列 nums ，按任意順序 返回所有不重復的全排列。

思考分析以及代碼

這一題和前面的做過的兩個題目有所關聯：
leetcode 46. 全排列 思考分析
再加上leetcode 491. 遞增子序列 思考分析類似的去重操作。
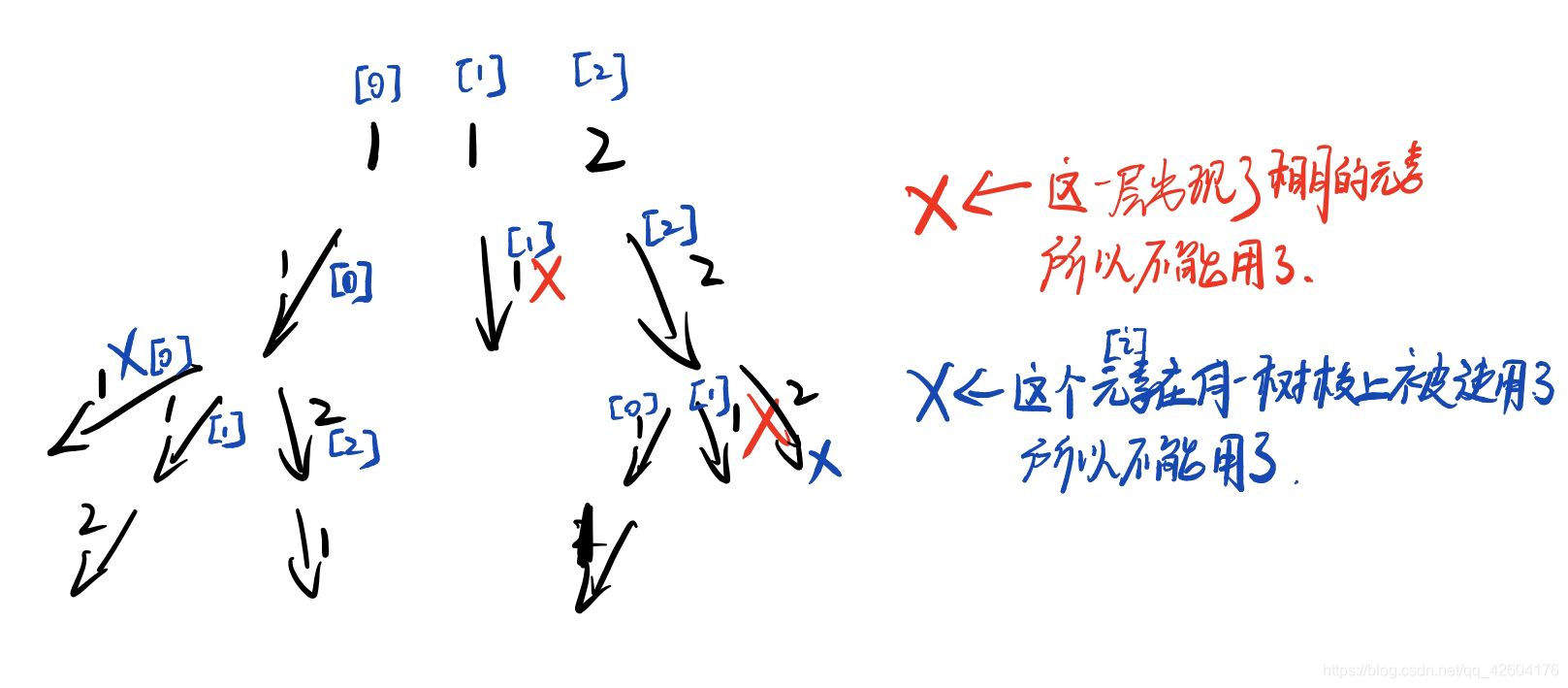
先畫出解空間樹的圖：
紅色部分才是真正意義上的去重：值相同的跳過。
藍色部分指的是我們用過的元素不能再用了。在組合問題中由于for循環進入下一層是i+1，所以本身就將用過的元素排除了。然而在排列問題中，我們可能要用到序號靠前且沒有使用過的元素，所以需要通過限制去除。

這里的“去重”我用到了兩個數組：

vector<bool> used;
int usedArray[21]={0}; //這里使用數組來進行去重操作。

used存放的是樹深度上的元素是否“用過”的信息，用過的元素將不會再用。
usedArray存放的是樹這一層上的元素是否是重復的元素，重復的元素將不會再用。
所以used是全局變量，usedArray是本層的局部變量。
下面是代碼：

class Solution {
public:vector<vector<int>> result;vector<int> res;vector<bool> used;void backtracking(vector<int>& nums){//如果res元素個數和nums一樣多說明一個排列已經完成if(res.size() == nums.size()){result.push_back(res);return;}int usedArray[21]={0}; //這里使用數組來進行去重操作。for(int i=0;i<nums.size();i++){//used存放的是樹深度上的元素是否“用過”的信息，用過的元素將不會再用。//usedArray存放的是樹這一層上的元素是否是重復的元素，重復的元素將不會再用//元素可以是重復但沒有用過。if(used[i] == false && usedArray[nums[i]+10] ==0){usedArray[nums[i]+10] =1;//處理結點；used[i]=true;res.push_back(nums[i]);//遞歸,探索下一層backtracking(nums);		//遞歸//回溯，撤銷處理結果res.pop_back();used[i]=false;}//如果這個元素已經用過了，不做處理}return;}vector<vector<int>> permuteUnique(vector<int>& nums) {result.clear();res.clear();//裝載used數組for(int i=0;i<nums.size();i++)  used.push_back(false);//開始回溯backtracking(nums);return result;}
};

劍指 Offer 38. 字符串的排列

https://leetcode-cn.com/problems/zi-fu-chuan-de-pai-lie-lcof/
這一題類似。