原題鏈接
旋轉圖像備戰技術面試？力扣提供海量技術面試資源，幫助你高效提升編程技能，輕松拿下世界 IT 名企 Dream Offer。
https://leetcode.cn/problems/rotate-image/
算法分析
????????若矩陣的行列數為N，設i表示行索引，i屬于[1,N]，按照題意旋轉矩陣則可以理解為我們需要將第i行的所有元素轉換為第N-i+1列，如示例1所示，第1行為[1,2,3]，旋轉后的第1行則變成了第3列，第2行與第3行同樣如此。
????????PS:經現有測試該方法適用于行列數相同的矩陣，但不確定是否適用于行列數不同的矩陣。
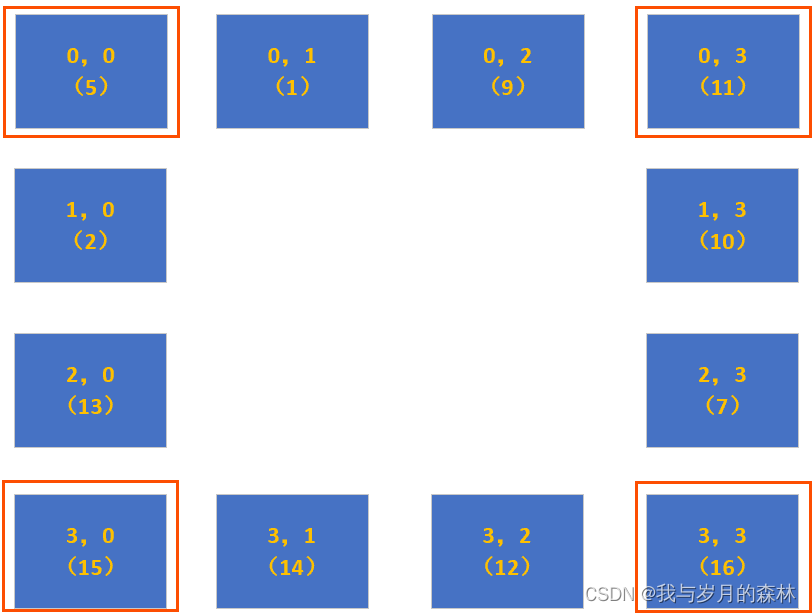
????????如圖（1）索引分別為(0,0)，(0,1)，(0,2)，(0,3)，(1,3)，(2,3)，(3,3)，(3,2)，(3,1)，(3,0)，(2,0)，(1,0)的點圍成了一個圈，假設我們稱之為矩陣圈。那么由外向內我們依次稱為第1層矩陣圈，第2層矩陣圈，……第n層矩陣圈。圖（1）所示有兩個矩陣圈，第1層矩陣圈的索引集合為[(0,0)，(0,1)，(0,2)，(0,3)，(1,3)，(2,3)，(3,3)，(3,2)，(3,1)，(3,0)，(2,0)，(1,0)]，第2層矩陣圈的索引集合為[(1,1)，(1,2)，(2,2)，(2,1)]。
????????如圖（1）和圖（2）我們可以發現通過對每個矩陣圈的旋轉即可完成對整個矩陣的旋轉，而對矩陣圈的旋轉實際上就是對矩陣圈進行點交換。點交換的意思是交換矩陣圈四個邊上的點，并且每個點是相互對應的。
????????如圖（3）所示，第一次交換索引為(0,0)和索引為(0,3)的點，第二次交換索引為(0,0)和索引為(3,3)的點，第三次交換索引為(0,0)和索引為(3,0)的點，我們把這稱為矩陣圈的點交換。而這僅僅是矩陣圈的第一次點交換，假設該矩陣圈的行數和列數均為m，那么旋轉該矩陣圈則需要(m-1)次點交換。
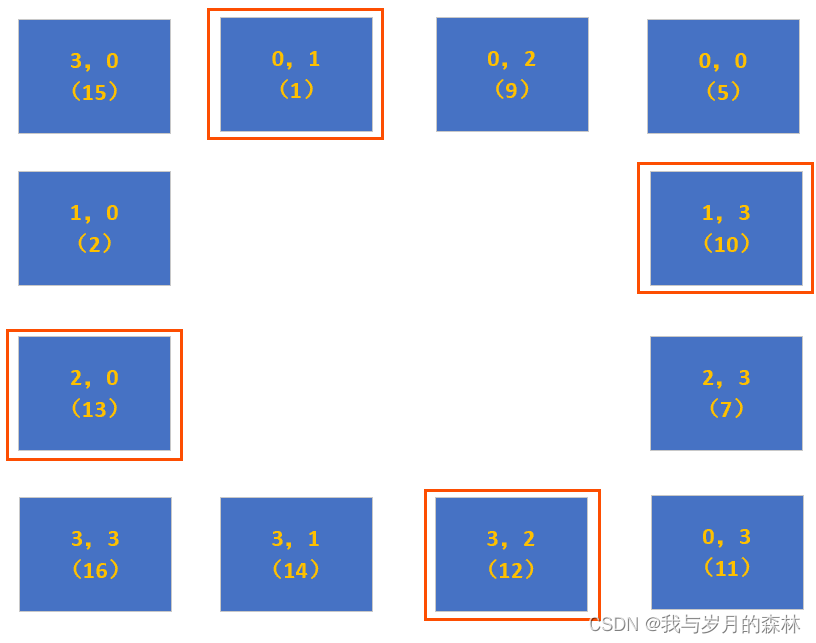
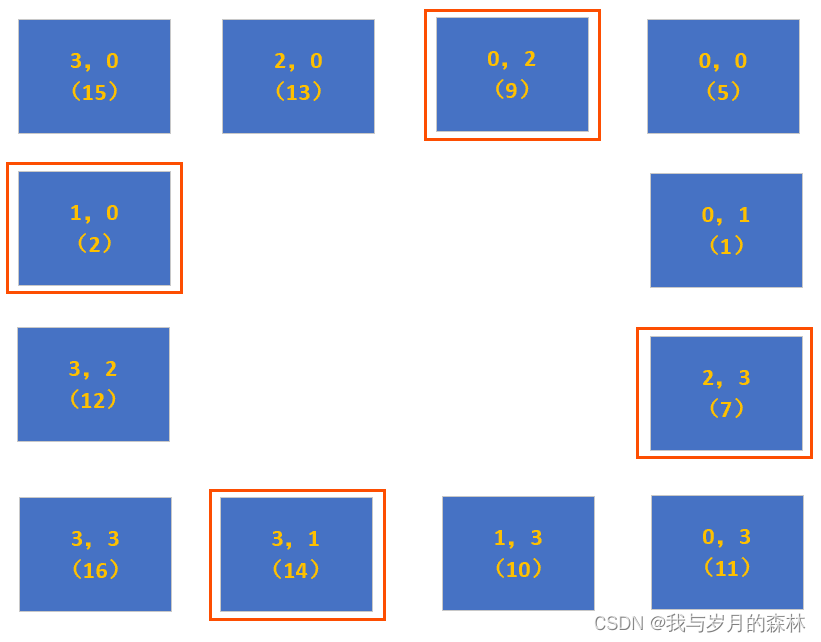
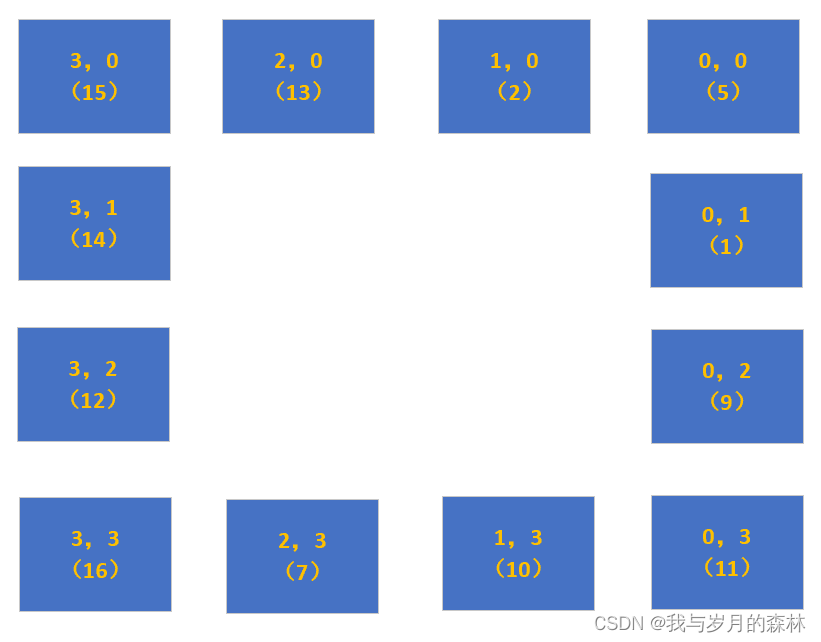
????????圖（3）（4）（5）（6）則為該矩陣圈的一次完整的90°旋轉。
????????為了從定量角度分析這個規律。首先我們可以定義四個變量rowA,rowB,colA,colB分別表示每一個矩陣圈的首行尾行以及首列尾列，并對它們進行初始化，rowA=0,rowB=m-1,colA=0,colB=m-1，rowA指向當前矩陣圈第一行，rowB指向最后一行，colA指向當前矩陣圈第一列，colB指向最后一列。其次我們再定義一個變量count，表示當前矩陣圈需要進行點交換的次數，count屬于[1,m-1]。那么該矩陣圈進行點交換的四個點的索引分別為：
(rowA,colA+count-1),? (rowA+count-1,colB),
(rowB,colB-count+1),? (rowB-count+1,colA)
????????我們只需要按照(rowA+count-1,colB),(rowB,colB-count+1),(rowB-count+1,colA)的索引順序分別與索引為(rowA,colA+count-1)的點進行交換即可，每完成一次點交換則count進行+1操作，當count等于m-1時表示該矩陣圈的90°旋轉完成。所以接下來需要收縮rowA,rowB,colA,colB四個變量，從而指向下一層矩陣圈，收縮操作即對rowA和colA進行+1操作，對rowB和colB進行-1操作，重復上述過程從外向內旋轉矩陣圈直至rowA、rowB、colA、colB四個變量的值相等則表明整個矩陣完成了90°的旋轉。
代碼示例（C#）?
public void Rotate(int[][] matrix)
{//定義變量int rowA = 0, rowB = matrix.Length - 1, colA = 0, colB = matrix[0].Length - 1, count = 1;//邏輯主體while (count <= colB - colA){//矩陣點交換(matrix[rowA][colA + count - 1], matrix[rowA + count - 1][colB]) = (matrix[rowA + count - 1][colB], matrix[rowA][colA + count - 1]);(matrix[rowA][colA + count - 1], matrix[rowB][colB - count + 1]) = (matrix[rowB][colB - count + 1], matrix[rowA][colA + count - 1]);(matrix[rowA][colA + count - 1], matrix[rowB - count + 1][colA]) = (matrix[rowB - count + 1][colA], matrix[rowA][colA + count - 1]);//矩陣圈收縮if (count == colB - colA){colA++;colB--;rowA++;rowB--;count = 1;}else count++;}
}算法解說?
????????結合算法分析過程，我們將矩陣的旋轉轉換為矩陣圈的旋轉，然后將矩陣圈的旋轉轉換為矩陣點的交換，也就是說矩陣旋轉的本質就是矩陣中各個元素的交換，實際上我們從圖（1）和圖（2）就可以發現，轉換前的矩陣的第一行變成了轉換后的矩陣的最后一列，但是本文的解題思路并未采取這種方式。
?????? 由于每個矩陣圈都有四條邊，所以旋轉矩陣圈就是在交換四個邊上指定的元素，具體的思路算法分析中已經描述得比較詳盡，對于如何將分析過程轉換為代碼，對于多數算法題來說本質上都是明確兩個重點，一個是變量，一個是邏輯主體。本題中所用到的變量包括用于明確當前矩陣圈的四個指針，還有一個用于記錄當前矩陣圈進行點交換的次數。而邏輯主體則包括矩陣點交換和矩陣圈收縮，同時需要明確邏輯主體退出的條件。
