第一節 行列式的基本概念和性質

一、基本概念

①逆序

1,2和2,1是一對逆序

②逆序數

1,2,3,5,4的逆序數為1;1,3,2,5,4逆序數為4;

③行列式

④余子數和代數余子數

行列式挖掉一個數(例如aij),將原行列式去掉i行j列的行列式M,則M為余子數,代數余子數記為Aij,如果(i+j)為偶數,Aij=M,如果(i+j)為奇數,則Aij=-M

知識補充:使用定義法計算行列式

以三階行列式為例:

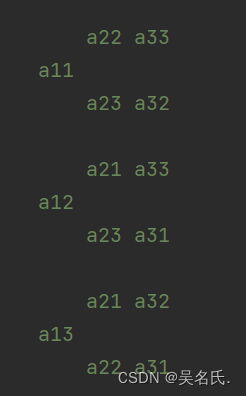
符號確定,列序號的逆序數的個數為奇數,則為負號,逆序數的個數為偶數,則為正號

所以 D = a11 * a22 * a33 + a12 * a23 * a31 + a13 * a21 * a32 - a11 * a23 * a32 - a12 * a21 * a33 - a13 * a22 * a31

二、幾個特殊的行列式

①對角、上(下)三角行列式

②范德蒙行列式

三、行列式的計算性質

(一)一般行列式轉化為上(下)三角行列式的性質

①行列式和置換行列式相等

置換行列式:行列交換,aij和aji交換

②對調兩行(或兩列),改變符號

③對某行(或某列)可以直接把公因子提出來

推論1:如果某行(或某列)全為0,那么行列式結果為0

推論2:如果某兩行(或某兩列)相同,那么行列式結果為0

推論3:如果某兩行(或某兩列)成比例,那么行列式結果為0

④行列式某行(或列)的每個元素皆為兩數之和時,行列式可分解為兩個行列式之和,即:

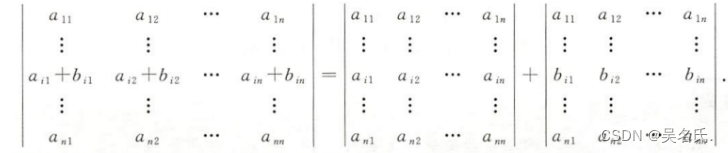
⑤行列式的某行(或列)的倍數加到另一行(或列),行列式不變,即

k為任意常數

(二)行列式的降階性質

1.行列式等于行列式某行(或列)元素與其對應的代數余子式之積的和,即

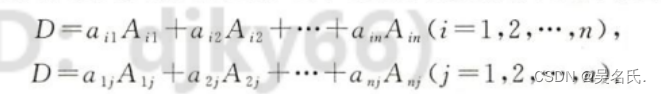
2.行列式的某行(或列)元素與另一行(或列)對應元素的代數余子式之積的和為零即

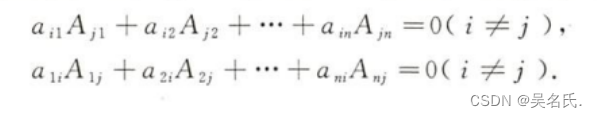
第二節 行列式的應用-克拉默法則