1.插入排序

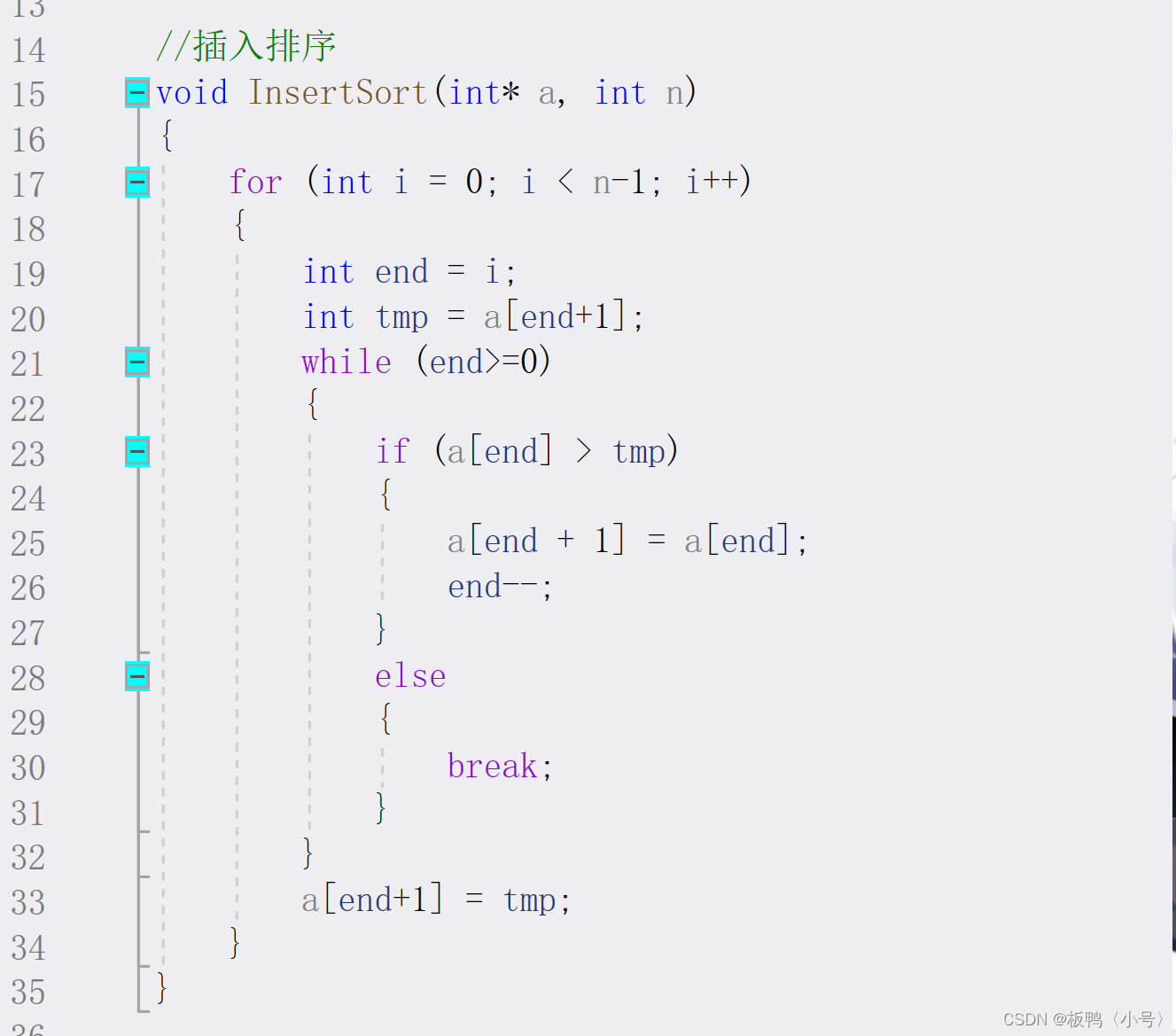
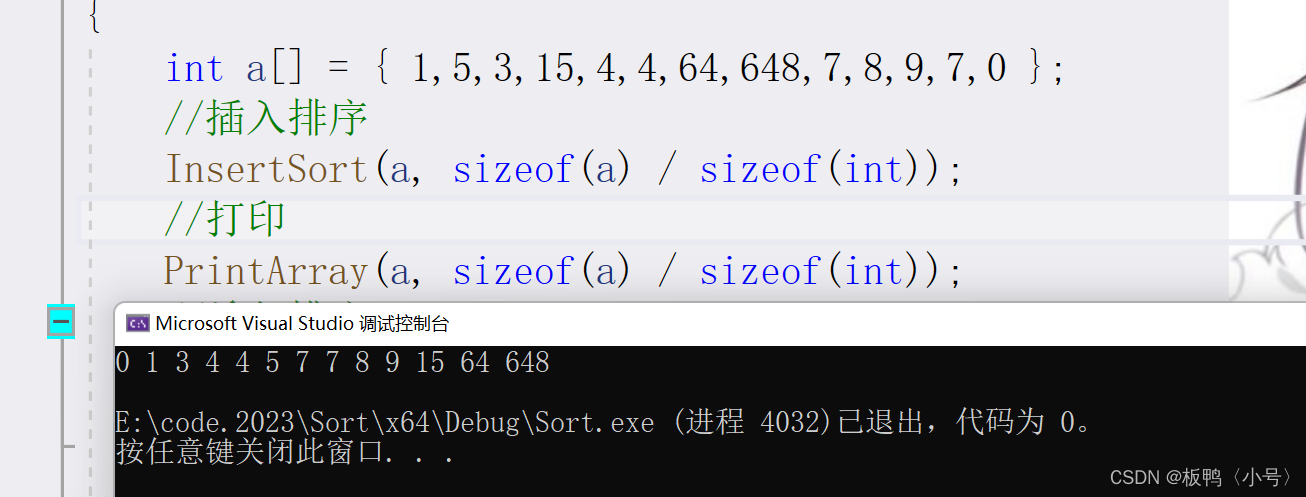
由上面的動圖可以知道插入排序的邏輯就是從第一個元素開始往后遍歷，如果找到比前一個元素小的（或者大的）就往前排，所以插入排序的每一次遍歷都會保證前面的數據是有序的，接下類用代碼進行講解。

我們這里傳兩個參數，一個是數組，一個是數組元素的個數。

排序接口我們采用大事化小的想法來進行講解，?我們先來思考單趟遍歷要達成的目標。我們每次遍歷的主角其實就是我們要操縱的那一個元素，比如我們要排第四個元素，按照插入排序的邏輯，前三個元素我們是已經有序了，所以我們接下來的操作就是將我們的主角元素跟前面的元素進行比較，如果元素比前面的小我們就跟前面的交換（我們這里實現升序排序），以此循環往復，直到遇到比它還小的元素我們就終止循環，所以我們就可以理解里面這層while循環的意思了，循環結束的時候不要忘記把元素放到停止循環的end下標位置上，有的同學可能一時間沒有理解到為什么最后下標的位置是end+1，其實這是因為在結束while循環之前我們的end是減一過的，所以才要給他加回去。

然后我們的for循環就是控制我們的主角啦，就是控制后面的每一個元素跟前面已經排序好的元素進行比較。

插入排序最壞的時間復雜度O（n^2）

最好的情況就是這個數組已經有序的時候時間復雜度為O(n)

2.希爾排序

?上訴動態演示就是希爾排序，大家看到這個演示的時候肯定會兩眼一黑，看不懂它是如何進行排序的，希爾排序的邏輯是有點復雜，但是我相信在我講了它的實現思路之后對希爾排序也會有一個比較清晰的理解。

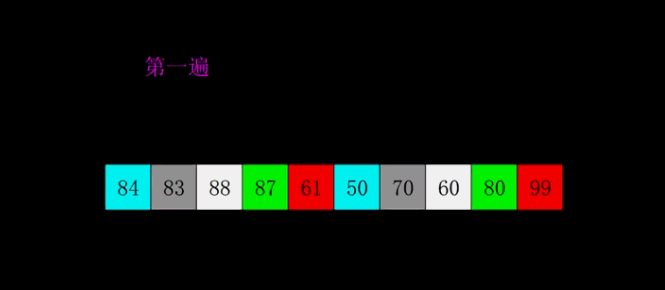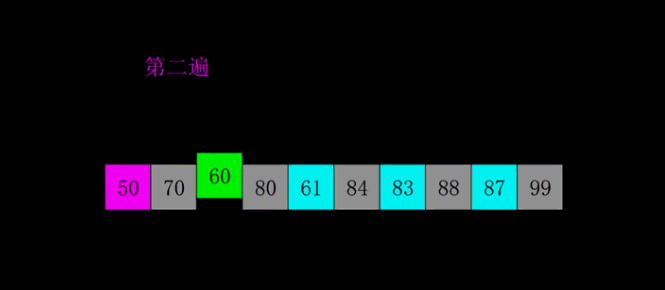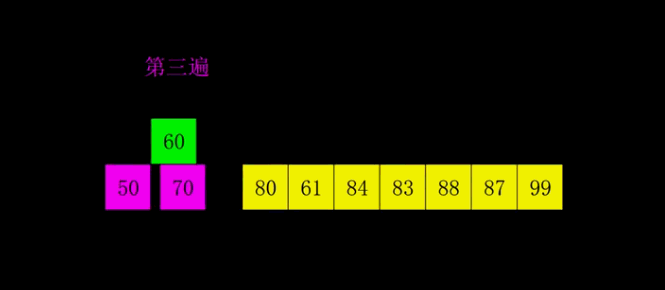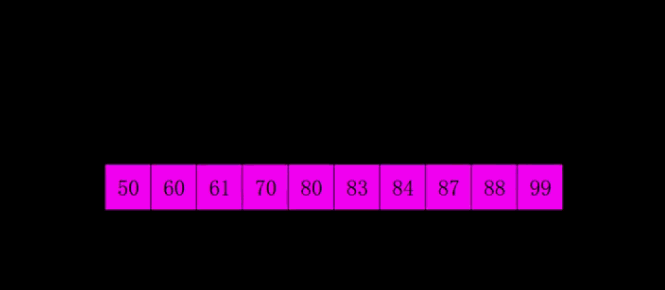
希爾排序可以相當于插入排序的pro版本，這是因為它的邏輯雖然比插入排序復雜，但是卻是建立在插入排序之上，插入排序的核心思想是遍歷每一個元素去跟前面已經排好序的元素進行比較，希爾排序有一個預排序的過程，就是說通過給定一個gap（變量名）來控制一個間距，使下標為end的元素跟end+gap來比較，這個預排序就是使一個無序數組接近有序數組，在預排序完成之后再用插入排序使數組有序。其實到這里大家就會發現，如果用這里的思想去理解插入排序的話，插入排序實際上就是gap為1的情況嘛。

我們用代碼來加深理解。

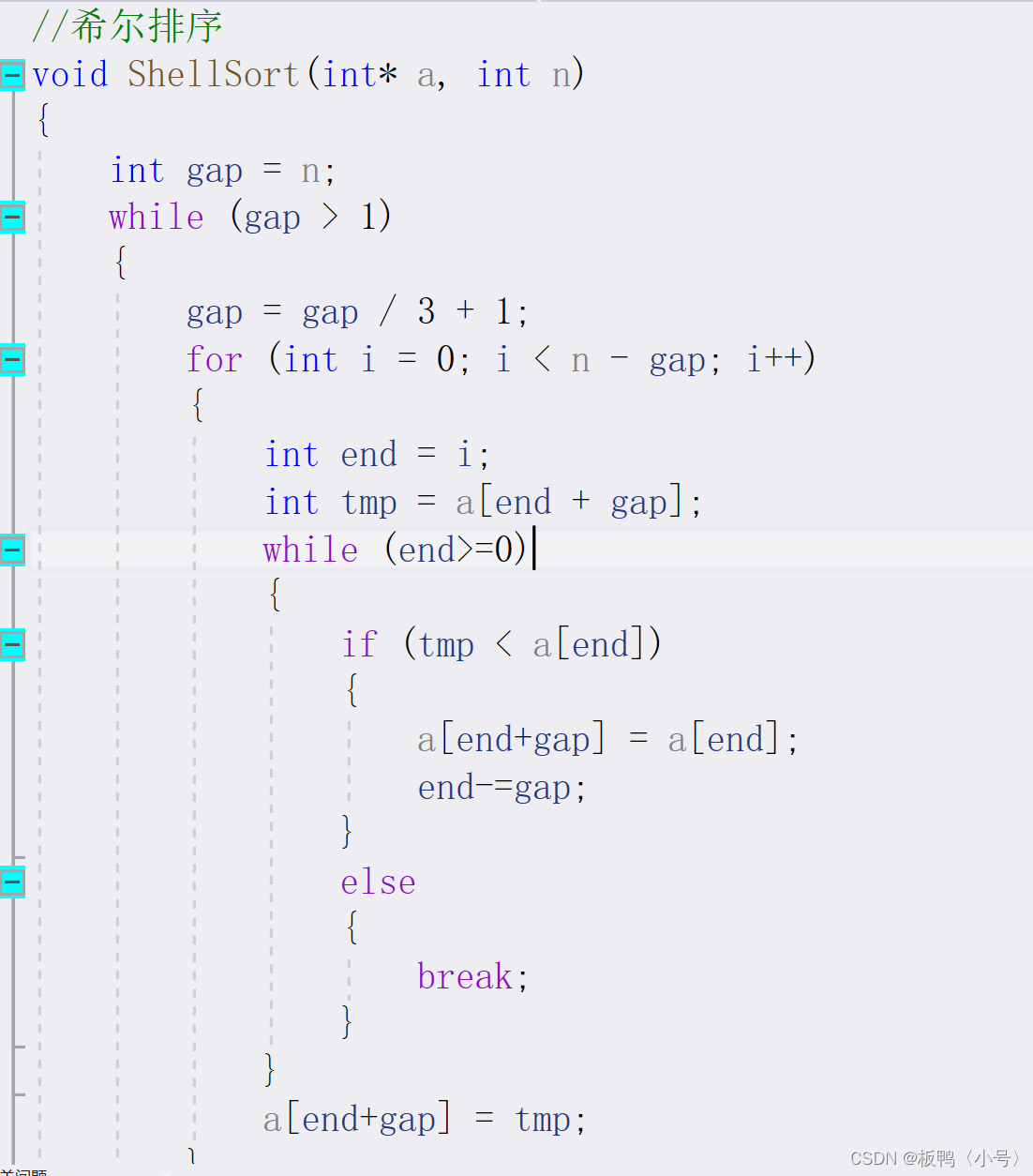
這是希爾排序的代碼，我們可以看到gap的初始值設置的是數組的長度，那下面的while循環時什么意思呢？我們先來理解最里層的while循環，最里層的while循環是不是有一種很眼熟的感覺?它就是我們的插入排序的思想，只不過插入排序是間隔為一進行比較，希爾排序是間隔為gap進行比較，我們再看外面這層for循環，這層for循環控制的就是end的下標，跟插入排序也非常的相似，只不過這里的for循環結束的條件是n-gap，因為既讓我們當前下標的元素要跟后一個相比，那總不能讓end+gap的下標超出界限吧。

最后再來看最外層的while循環，它的作用就是控制gap的值。我們這里得要知道gap越大，這一趟預排序就越不能做到很有序的程度，但好處就是耗時短，gap的值越小就是相反的情況，但是不要忘記了，一個數組越有序，插入排序處理得就越快，希爾排序也是一樣的，所以為了達到理想的時間復雜度，我們的做法就是將gap的值由大到小。

接下來來說說gap的值如何來設置，gap的值該如何來設置是沒有一個統一的說法的，但是有一個大佬想出的一個比較好的方法是用數組長度來充當第一次的gap值，每一次循環完就將gap的值/3+1這是為了避免上一個gap為二的時候下一次gap直接變為0了。

所以我們的希爾排序最后一趟就是我們的插入排序，只不過這個時候數組已經非常接近有序了。

我們的希爾排序最壞的情況下時間復雜度是O(n^2),平均是O(n^1.3)。