---

0x00 XOR 運算在 2 的補碼加減法中的應用

2 的補碼加減法的特點是，當從某個數中減去負數時，將其轉換為正數的加法來計算，并將減去正數的情況轉換為負數的加法來計算，從而將所有減法運算轉換為加法運算。在這種情況下，兩個數的加法運算中產生進位的情況是在加法位的所有位都為 1 時。

換句話說，可以使用 AND 門來檢測產生進位的情況。在兩個數的加法運算中，進位傳播的情況是在加法位的兩個位中只有一個被設置為 1 時。這是因為從較低位傳遞上來的進位位會再次傳遞到下一個位，因此可以使用 XOR 門來檢測進位傳播的情況。

• carry-generate funciton：
• carry-propagate function：

0x01 BCD 運算

在 BCD 中，使用4位值作為操作數，但由于只表示 0 到 9 的數字，因此只使用 0000 到 1001 的二進制數，而不使用 1010 到 1111 的二進制數（don't care）。

因此，不能使用常規的 2'complement 運算來計算，需要額外的處理：如果 4 位二進制數的運算結果在 1010 到 1111 的范圍內，需要將 6 (即 0110)，添加到運算結果中。

BCD 運算例子

0x02 BCD 加法器的實現

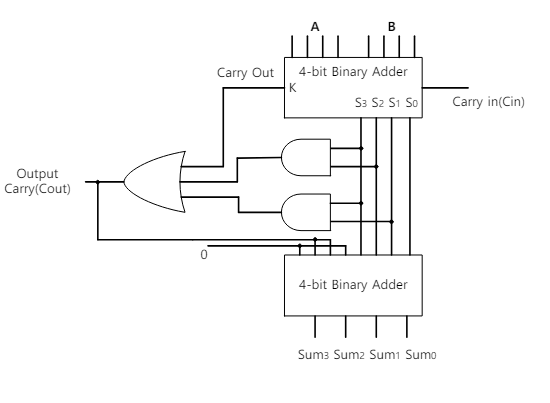
關于 BCD 加法器的結果和模擬過程進行說明（Verilog源代碼，輸出示例，詳細描述過程）。

💬 Design source：

module BCD2(input Cin,input a1,input a2,input a3,input a4,input b1,input b2,input b3,input b4,output sum1,output sum2,output sum3,output sum4,output cout);
wire s1,s2,s3,s4;
wire c1,c2,c3,c4;
wire C1,C2,C3,C4;assign s1 = (a1^b1)^Cin;
assign c1 = (Cin && (a1^b1)) || (a1 && b1);assign s2 = (a2^b2)^c1;
assign c2 = (c1 && (a2^b2)) || (a2 && b2);assign s3 = (a3^b3)^c2;
assign c3 = (c2 && (a3^b3)) || (a3 && b3);assign s4 = (a4^b4)^c3;
assign c4 = (c3 && (a4^b4)) || (a4 && b4);///
assign cout = (c4 || (s3 && s4) || (s2 && s4));assign sum1 = s1;
assign C1 = (0 && (s1^0)) || (s1 && 0);assign sum2 = (s2^cout)^C1;
assign C2 = (C1 && (s2^cout)) || (s2 && cout);assign sum3 = (s3^cout)^C2;
assign C3 = (C2 && (s3^cout)) || (s3 && cout);assign sum4 = (s4^0)^C3;
assign C4 = (C3 && (s4^0)) || (s4 && 0);endmodule

💬 Testbench：

`timescale 1ns / 1psmodule BCD2_tb;
reg Cin,a1,a2,a3,a4,b1,b2,b3,b4;
wire sum1,sum2,sum3,sum4,cout;BCD2 u_BCD2 (.Cin(Cin ),.a1(a1 ),.a2(a2 ),.a3(a3 ),.a4(a4 ),.b1(b1 ),.b2(b2 ),.b3(b3 ),.b4(b4 ),.sum1(sum1 ),.sum2(sum2 ),.sum3(sum3 ),.sum4(sum4 ),.cout(cout )
);initial beginCin = 1'b0;a1 = 1'b0;a2 = 1'b0;a3 = 1'b0;a4 = 1'b0;b1 = 1'b0;b2 = 1'b0;b3 = 1'b0;b4 = 1'b0;
endalways@(Cin or a1 or a2 or a3 or a4 or b1 or b2 or b3 or b4) beginCin <=#10 ~Cin;a1 <= #20 ~a1;a2 <= #40 ~a2;a3 <= #80 ~a3;a4 <= #160 ~a4;b1 <= #320 ~b1;b2 <= #640 ~b2;b3 <= #1280 ~b3;b4 <= #2560 ~b4;
endinitial begin#5120$finish;
endendmodule

🚩 運行結果如下：

📜 Schematic：

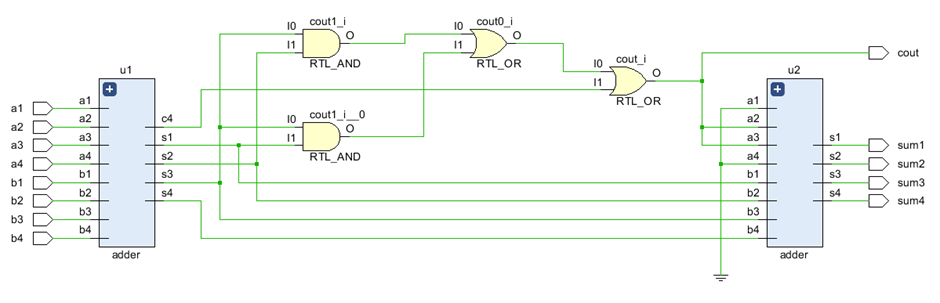實現的 BCD 加法器是一種將 4 位加法器運算結果轉換為 BCD 表示的設備。如果運算結果是一個大于 9 的數字，我們只需加上 6 (0110)。為了實現這一點，該裝置由兩個加法器電路組成：一個用于執行 4 位加法器運算，另一個電路用于在第一個運算結果大于 9 時加上 0110（補償電路）。

0x03 補充：Single-level 16 bit 超前進位加法器

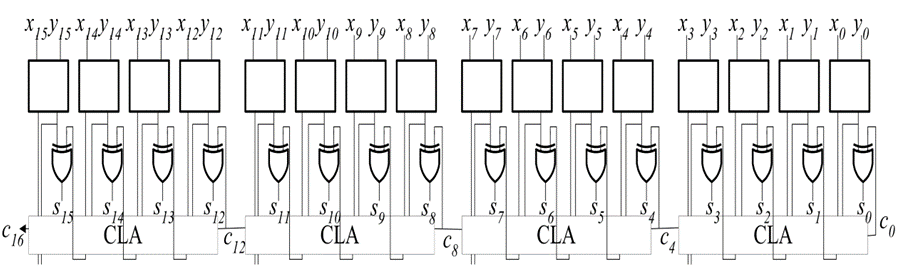
四個 4 位超前進位加法器可以合并成一個 16 位超前進位加法器。它是四個并行結構的串行連接，是并行和串行結構的混合體。

0x04 補充：2-level 16-bit 超前進位加法器

2 級 16 位超前進位加法器是一種通過使用雙 CLA 發生器，比單級 16 位超前進位加法器更能減少通過柵極所需的延遲的結構。

2-level 16-bit Carry Look-ahead Adder

📌 [ 筆者 ]?  ???(韓)
📃 [ 更新 ]? ?2022.9.20
? [ 勘誤 ]?? /* 暫無 */
📜 [ 聲明 ]? ?由于作者水平有限，本文有錯誤和不準確之處在所難免，本人也很想知道這些錯誤，懇望讀者批評指正！

📜 參考資料? Introduction to Logic and Computer Design, Alan Marcovitz, McGrawHill, 2008 Microsoft. MSDN(Microsoft Developer Network)[EB/OL]. []. . 百度百科[EB/OL]. []. https://baike.baidu.com/.