在機器學習的旅程中，我們已經接觸了多種學習算法。在監督學習中，選擇使用算法 A 還是算法 B 的重要性逐漸減弱，而更關鍵的是如何在應用這些算法時優化目標。這包括設計特征、選擇正則化參數等因素，這些在不同水平的實踐者之間可能表現出截然不同的效果。

在支持向量機（Support Vector Machine，SVM）這一強大而受歡迎的算法中，我們發現了一種更為清晰且強大的學習方式，尤其在處理復雜非線性方程時。在這篇文章中，我們將深入研究支持向量機，了解其優化目標和數學定義。

優化目標的起點

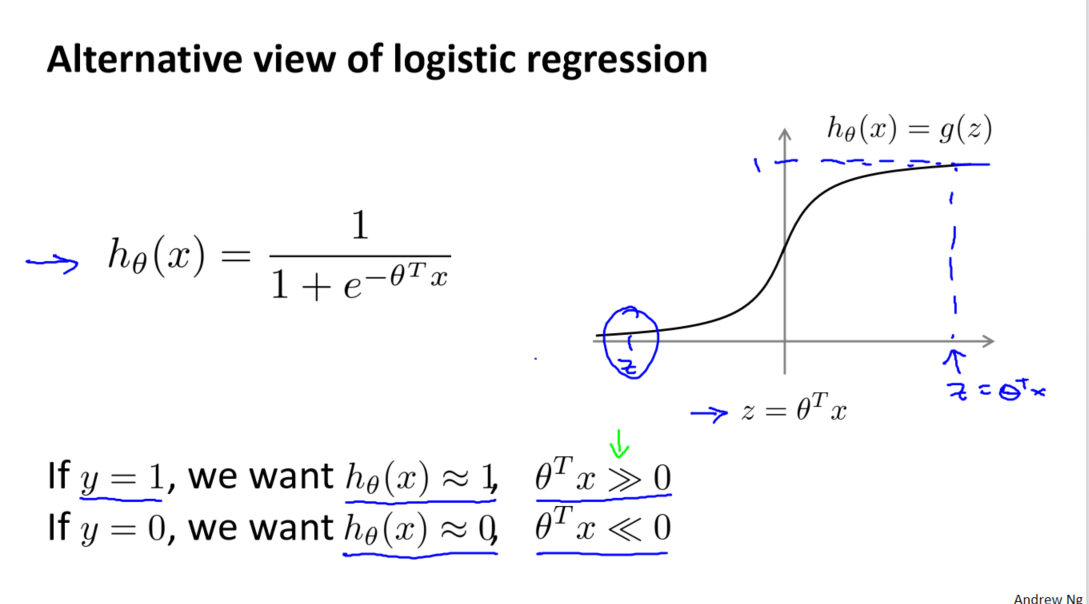
與以往一樣，我們從優化目標開始。在邏輯回歸中，我們熟悉的是假設函數和 S 型激勵函數。然而，支持向量機采用了一種更為直接和強大的方式來學習。我們將逐步從邏輯回歸演變到支持向量機。

首先，我們回顧了邏輯回歸中的代價函數，其中每個樣本對總代價函數都有貢獻。對于樣本（𝑥，𝑦），我們考慮了當 𝑦 = 1 時的情況，其中代價函數項為 ?log(1 ? 1 / (1 + 𝑒^(?𝑧)))。通過觀察這個函數在 𝑧（表示為 𝜃^𝑇𝑥） 增大時的行為，我們理解了邏輯回歸在觀察正樣本時試圖將 𝜃^𝑇𝑥 設得非常大的原因。

構建支持向量機

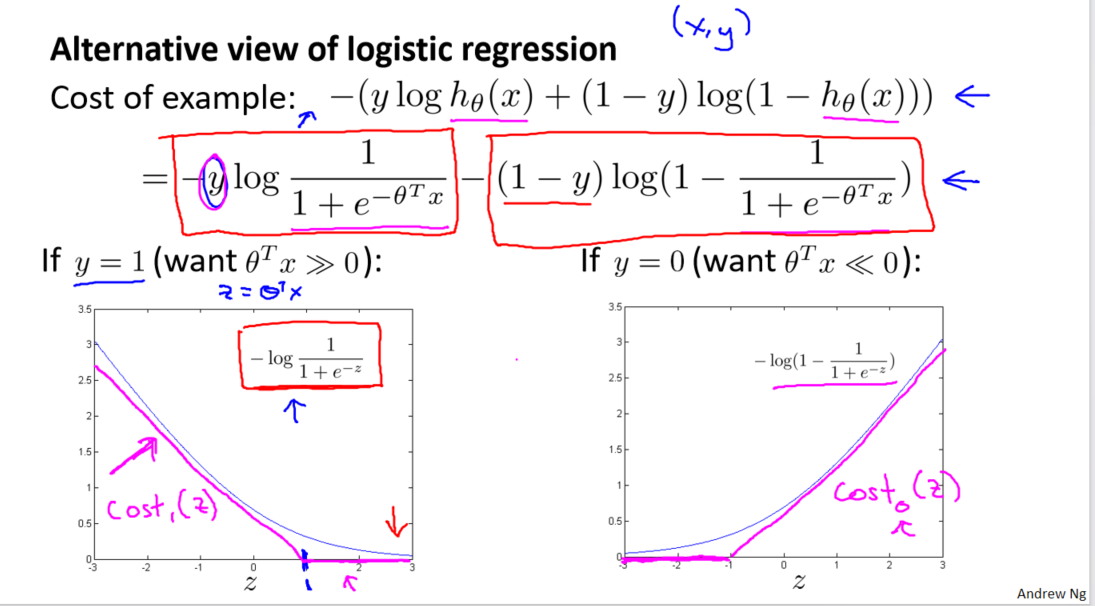
現在，我們開始構建支持向量機。我們將邏輯回歸中的代價函數進行修改，引入兩條新的線段，分別對應于𝑦 = 1 和 𝑦 = 0 的情況。這為支持向量機的建立奠定了基礎。

我們引入兩個新的代價函數，分別命名為cos𝑡1(𝑧)和cos𝑡0(𝑧)，其中 𝑧 表示 𝜃^𝑇𝑥。這兩個函數在數學上是連續的線段，代表了支持向量機的優化目標。

支持向量機的代價函數形式為 𝐶 × cos𝑡1(𝑧) + cos𝑡0(𝑧)，其中 𝐶 是一個權衡項，代替了邏輯回歸中的正則化參數 𝜆。通過調整 𝐶 的大小，我們可以靈活地調整對擬合訓練樣本和正則化項的重視程度。

SVM 的數學定義

支持向量機通過最小化優化目標函數來學習參數，這一目標函數包含了代價函數和正則化項。通過將邏輯回歸中的正則化參數 𝜆 替換為 𝐶，我們得到了支持向量機的數學定義。最終，支持向量機的假設函數直接預測 𝑦 的值是 1 還是 0，根據 𝜃^𝑇𝑥 大于或等于 0 的情況。

參考資料：

[中英字幕]吳恩達機器學習系列課程

黃海廣博士 - 吳恩達機器學習個人筆記