1.歸并排序
基本思想:
歸并排序是建立在歸并操作上的一種有效的排序算法,該算法是采用分治法的一個非常典型的應用。將已有序的子序列合并,得到完全有序的序列;即先使每個子序列有序,再使子序列段間有序。若將兩個有序表合并成一個有序表,稱為二路歸并。 歸并排序核心步驟:
相當于每次把待排數據分為兩個子區間,如果每個子區間有序,再讓兩個子區間歸并起來也有序,那整體就有序了。我們可以按照二叉樹的思想,把子區間再分為兩份,使子區間的子區間有序.......直到子區間分無可分為止。
具體過程如下:
那該如何讓兩個有序子區間歸并呢?
直接在數組中肯定不行,這樣會發生數據的覆蓋。所以我們可以像之前合并兩個有序數組一樣,另外開辟一個空間tmp,依次比較兩個有序子區間的值,每次比較后把較小的放在tmp中,如果其中一個子區間提前結束,就把另外一個子區間的剩余的數據全放進tmp,最后把tmp中的數據拷貝回原數組。
使用遞歸實現:
#include<stdio.h> #include<stdlib.h> void _MegeSort(int* a, int begin, int end,int*tmp) {//只剩一個數據,遞歸結束if (begin == end){return;}int mid = (begin + end) / 2;//遞歸子區間,分為兩部分_MegeSort(a, begin, mid, tmp);_MegeSort(a, mid+1, end, tmp);int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int j = begin;//兩部分比較,每次小的放入tmpwhile (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}//哪部分有剩余,全部放入tmpwhile (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}//拷貝到原數組memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1)); } void MegeSort(int* a, int n) {int* tmp = (int*)malloc(sizeof(int) * n);_MegeSort(a, 0, n - 1, tmp);free(tmp); }void Print(int* a, int n) {for (int i = 0; i < n; i++){printf("%d ",a[i]);}printf("\n"); } int main() {int a[] = { 1,4,9,6,3,5,2,8,10,7,11,1};MegeSort(a, sizeof(a) / sizeof(int));Print(a, sizeof(a) / sizeof(int));return 0; }注意:
1.?因為每次遞歸的子區間都不一定是從0開始的,所以我們拷貝數據時,最好從begin的位置開始:
//拷貝到原數組 memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));2. 在代碼中j作為tmp的坐標,每次往tmp中放入數據后都要加一,但不能初始化為0,否則每次遞歸進入,j的值都會清0,所以最好初始化:j=begin
歸并排序的復雜度:
時間復雜度:O(N*logN)
歸并排序每次遞歸都要把待排數據分為兩份,相當于二分法,那一共有logN層遞歸,而每次遞歸都要比較數據,要把每個數據都遍歷一遍,每層的時間復雜度就是O(N),所以總共的時間復雜度是O(N*logN)。
空間復雜度:O(N)?
剛開始就開辟了空間,此時就已經是O(N)了,而遞歸過程中函數棧幀的創建是logN,所以總的空間復雜度是:O(N+logN),但是量級沒變,還是O(N)。
2.非遞歸實現歸并排序
非遞歸實現歸并排序,我們只需模擬上述的遞歸過程即可,把遞歸過程轉換為:把數據先分為2個一組,全部歸并一遍,拷貝回原數組,然后4個一組,全部歸并一遍,拷貝回原數組,再8個一組,?全部歸并一遍,拷貝回原數組,
那我們就可以設置一個gap,兩個數據為一組時,gap=1,每歸并一組數據就往后跳2*gap步,直到全部歸并一遍,再次分組,這次gap=2,每歸并一組數據往后跳2*gap步,直到全部歸并一遍,下次gap=4,跳2*gap步.....,直到gap>n就停止,
代碼如下:
void MegeSortNonR(int* a, int n) {int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail\n");return;}int gap = 1;while (gap < n){int j = 0;for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;//兩部分比較,每次小的放入tmpwhile (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}//哪部分有剩余,全部放入tmpwhile (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}}memcpy(a, tmp, sizeof(int) * n);gap *= 2;}free(tmp); }測試一下:
上面結果看起來,我們排序成功了,但是上述代碼真的對嗎?
上面代碼我們在測試時用的是8個數據,但是如果用9個、10個等,就會發現排序并不會成功,可能程序還會崩掉,這是為什么呢?
因為我們在分組時,是按照固定的2的次方分的,一旦數據個數不是2、4、8的次方,后面歸并時就會發生越界問題。
下面我們給10個數據打印一下邊界,會發現,有三種越界的方式,:
那我們對這三種情況分別做一下處理:
第1、2種情況出現時,我們直接break,第三種情況,我們修改邊界,令end2=n-1,但是注意直接break后,第1、2種情況往tmp中歸并時會少一部分數據(如上圖藍框所示),所以最后把tmp的數據往a中拷貝時,不能一次性全部拷貝回去,否則a中這些數據就永遠丟失了,所以最好歸并一段,拷貝一段,這樣拷貝過去的數據只會把前面的數據覆蓋,沒參與歸并的數據還在a中。
代碼如下:
void MegeSortNonR(int* a, int n) {int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail\n");return;}int gap = 1;while (gap < n){int j = 0;for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;if (end1 >= n || begin2 >= n){break;}//修正if (end2 >= n){end2 = n - 1;}//兩部分比較,每次小的放入tmpwhile (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}//哪部分有剩余,全部放入tmpwhile (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}//歸并一段,拷貝一段memcpy(a+i, tmp+i, sizeof(int) * (end2-i+1));}gap *= 2;}free(tmp); }
3.計數排序
基本思想:
1. 統計每個數據出現的次數。
2. 根據數據的次數排序。?
如果我們要排序的數在0~9之間,我們可以像上面一樣開辟10個int大小的空間,統計待排數據中每個數據的個數,在開辟出的數組的相應下標處計數,那如果我們要排序的數據在100~109之間呢?難道開辟110個空間嗎?
當然不是,我們可以做相對映射,在開辟空間之前,先找到待排數據中的最小值和最大值,開辟空間的大小就是:sizeof(int)*(max-min+1),開辟出的數組下標應該是:0~9,0~9下標的位置分別對應的是100~109,計數時,在下標為該數據減待排數據中的最小值的位置統計次數,例如:109就在109-100=9的下標處統計次數,統計完排序的時候再加上最小值即可。
代碼如下:
#include<stdio.h> #include<stdlib.h> void CountSort(int* a, int n) {int min = a[0], max = a[0];//找最大值和最小值for (int i = 0; i < n; i++){if (a[i] < a[0]){min = a[i];}if (a[i] > a[0]){max = a[i];}}int range = max - min + 1;int* count = (int*)malloc(sizeof(int) * range);memset(count, 0, sizeof(int) * range);//計數for (int i = 0; i < n; i++){count[a[i] - min]++;}//排序int k = 0;for (int j = 0; j < range; j++){while (count[j]--){a[k++] = j + min;}} } //打印函數 Print(int* a, int n) {for (int i = 0; i < n; i++){printf("%d ", a[i]);}printf("\n"); } int main() {int a[] = { 6,1,6,7,9,6,4,5,6,1 };CountSort(a, sizeof(a) / sizeof(int));Print(a, sizeof(a) / sizeof(int));return 0; }
計數排序的復雜度:
時間復雜度:O(N+range)
尋找最大值和最小值時,遍歷一遍數組,時間復雜度是:O(N),由于待排數據的范圍是range,排序時所耗費的時間復雜度是:O(range),所以最終的時間復雜度是:O(N+range)
如果知道N和range的大小,N大,就是O(N),range大,就是O(range)。
空間復雜度:O(range)
額外開辟的空間個數是range,所以空間復雜度就是:O(range)
4.排序的復雜度和穩定性
總結如下:

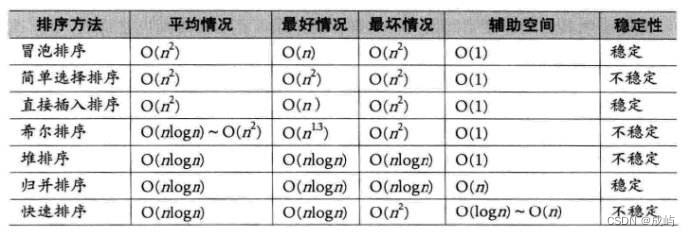
?以上就是排序學習的全部內容了,到這,數據結構的學習就告一段落了,近期會停更一段時間,用來復習,后面將繼續學習C++的知識,
未完待續。。。









)




)
![P1028 [NOIP2001 普及組] 數的計算](http://pic.xiahunao.cn/P1028 [NOIP2001 普及組] 數的計算)









)
