線性回歸是一種常用的回歸算法，用于建立輸入變量和連續輸出變量之間的關系。傳統的線性回歸算法通常依賴于繁瑣的數學推導和梯度計算。但是，隨著深度學習的興起，自求導的方法逐漸成為實現線性回歸算法的有效途徑。本文將介紹如何使用自求導的方法實現線性回歸算法，并討論其優勢和應用領域。

一、線性回歸算法簡介
線性回歸是一種建立輸入變量(X)和連續輸出變量(Y)之間線性關系的回歸分析方法。其基本原理是通過擬合一個線性模型來預測輸出變量，即 Y = b0 + b1*X，其中 b0 和 b1 是回歸系數，通過最小化殘差平方和來確定最佳的回歸系數。

二、傳統的線性回歸算法
傳統的線性回歸算法通常基于最小二乘法，通過最小化觀測值與預測值之間的殘差平方和來確定最佳的回歸系數。這需要對損失函數進行求導，然后使用梯度下降等優化方法來更新回歸系數。這個過程通常涉及到大量的數學推導和繁瑣的計算。

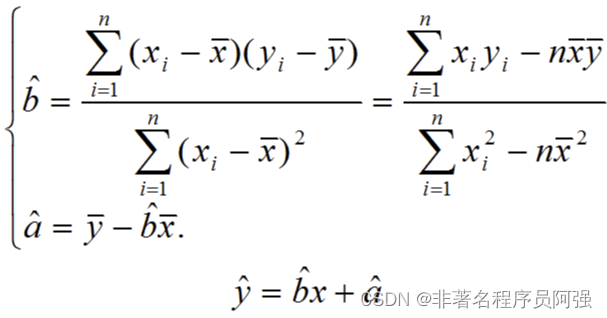
三、自求導的方法實現線性回歸
自求導的方法是使用深度學習框架中的自動求導功能來實現線性回歸。深度學習框架如PyTorch和TensorFlow提供了自動求導的功能，可以根據定義的模型和損失函數自動計算梯度。以下是使用自求導的方法實現線性回歸的基本步驟：

1. 數據準備: 首先，需要準備訓練數據，包括輸入變量(X)和目標變量(Y)。這些數據通常以矩陣或張量的形式表示。

2. 定義模型: 在深度學習框架中，可以定義一個包含一個線性層的模型。線性層的權重和偏置將作為回歸系數。

3. 定義損失函數: 使用均方誤差損失函數來衡量預測值與觀測值之間的差異。

4. 自動求導: 在深度學習框架中，可以通過調用backward()函數來自動計算損失函數對回歸系數的梯度。

5. 優化: 最后，可以使用梯度下降等優化方法來更新回歸系數，并迭代地進行訓練。

四、自求導方法的優勢
使用自求導的方法實現線性回歸算法具有以下優勢：

1. 簡化實現: 自動求導功能可以大大簡化線性回歸算法的實現過程，無需進行繁瑣的梯度計算和推導。

2. 高效性能: 自求導的方法可以利用深度學習框架的并行計算和優化算法，提高計算效率。

3. 擴展性: 自求導的方法可輕松應用于更復雜的模型和損失函數，如多變量線性回歸或非線性回歸。

4. 可視化: 深度學習框架提供了豐富的可視化工具，可以可視化模型和損失函數，方便分析和調試。

五、應用領域
自求導的方法廣泛應用于各個領域的線性回歸問題，特別是當數據集較大或復雜時，傳統的線性回歸算法往往效率較低。此外，自求導的方法還可以結合其他深度學習技術來解決更復雜的問題，如圖像識別、自然語言處理等。

結論:
使用自求導的方法實現線性回歸算法能夠簡化實現過程，提高計算效率，并具有良好的可擴展性。隨著深度學習技術的不斷發展，自求導的方法將在更多的回歸問題中得到廣泛應用。然而，在實踐中需要注意數據的預處理、模型的選擇和超參數的調整，以獲取更好的回歸結果。通過不斷研究和探索，自求導的方法將在機器學習和深度學習領域發揮越來越重要的作用。

人工智能的學習之路非常漫長，不少人因為學習路線不對或者學習內容不夠專業而舉步難行。不過別擔心，我為大家整理了一份600多G的學習資源，基本上涵蓋了人工智能學習的所有內容。點擊下方鏈接,0元進群領取學習資源,讓你的學習之路更加順暢!記得點贊、關注、收藏、轉發哦!掃碼進群領資料