時刻記住一句話:寫遞歸,1畫圖,2大腦放空!!!
意思是,自己寫遞歸題目,先用樣例給的數據畫圖,然后想一個超級簡單的思路,直接套上去就可以了。
上題干:
題目描述
給出正整數?n,要求按如下方式構造數列:
- 只有一個數字?n?的數列是一個合法的數列。
- 在一個合法的數列的末尾加入一個正整數,但是這個正整數不能超過該數列最后一項的一半,可以得到一個新的合法數列。
請你求出,一共有多少個合法的數列。
輸入格式
輸入只有一行一個整數,表示?n。
輸出格式
輸出一行一個整數,表示合法的數列個數。
輸入輸出樣例
輸入 #1復制
6輸出 #1復制
6說明/提示
樣例 1 解釋
滿足條件的數列為:
- 6
- 6,1
- 6,2
- 6,3
- 6,2,1
- 6,3,1
數據規模與約定
對于全部的測試點,保證 1≤n≤10^3。
說明
本題數據來源是 NOIP 2001 普及組第一題,但是原題的題面描述和數據不符,故對題面進行了修改,使之符合數據。原題面如下,謹供參考:
我們要求找出具有下列性質數的個數(包含輸入的正整數?n)。
先輸入一個正整數?n(n≤1000),然后對此正整數按照如下方法進行處理:
- 不作任何處理;
- 在它的左邊拼接一個正整數,但該正整數不能超過原數,或者是上一個被拼接的數的一半;
- 加上數后,繼續按此規則進行處理,直到不能再加正整數為止。
?這道題,不要想那么復雜。
題目給的數字是6,并且幫我們分析了答案如何來的:
- 6
- 6,1
- 6,2
- 6,3
- 6,2,1
- 6,3,1
第一步:畫圖
我們可以畫出一個簡易的樹狀圖:
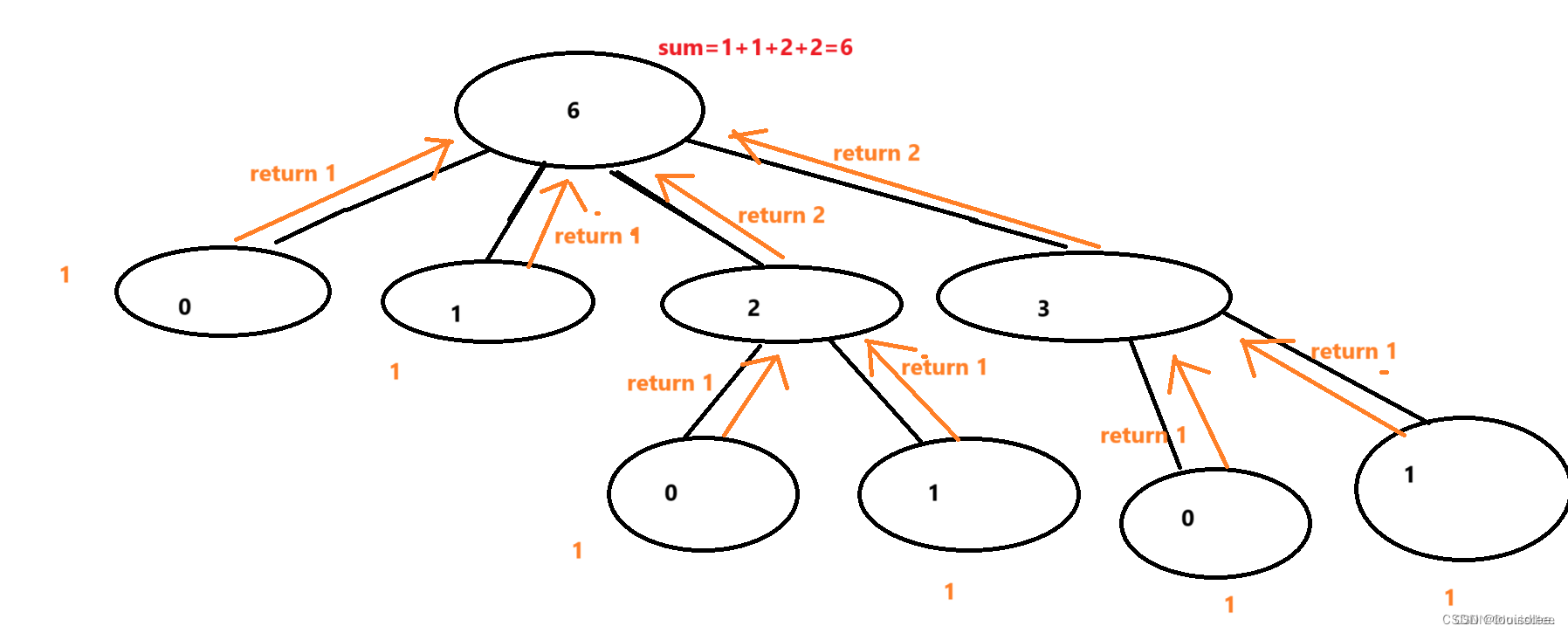
?
第二步:大腦放空,想一個最簡單的思路?
從i=0開始枚舉,一直枚舉到 6/2,
用 f【i】表示,6后面直接跟的數字是 i 的種數。(如果i=0,就代表,沒有跟任何數字)
所以答案就是 f【0】+ f【1】 +f【2】+f【3】
結束
寫出代碼:
const int N = 1e3 + 7;
int lxnb(int x) {int ans = 0;if (x == 1 or x == 0)return 1;for (int i = 0; i <= x / 2; i++) {ans += lxnb(i);}return ans;
}int main() {int n;cin >> n;cout << lxnb(n);
}然后,這樣的普通遞歸,無法,完成本題。
所以我們可以用到記憶化的方法,用一個數組記錄f【i】的值,如果f【i】已經被記錄了 ,那么我們就直接返回,它的值。
無腦塞進去就行了,哪里需要管這么多。。。。
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<cstring>
#include<string>
#include<algorithm>
#include<vector>
#include<cctype>
#include<map>
#include<set>
#include<queue>
#include<numeric>
using namespace std;
const int N = 1e3 + 7;
int flag[N];
int lxnb(int x) {int ans = 0;if (flag[x])return flag[x];if (x == 1 or x == 0)return 1;for (int i = 0; i <= x / 2; i++) {ans += lxnb(i);}return flag[x]=ans;
}int main() {int n;cin >> n;cout << lxnb(n);
}








)









