? ? ? 在算法設計中,雙指針是一種高效優化工具,主要用于線性數據結構(如數組(數組劃分和數組分塊常用)、鏈表、字符串),通過控制兩個指針的移動軌跡,將原本需要 O (n2) 時間復雜度的問題優化為 O (n),核心優勢是無需額外空間(通常為 O (1) 空間復雜度) 且邏輯直觀。其常見形式分為同向指針,對撞指針和快慢指針,具體解析如下:
(一) 同向指針
1. 定義與核心場景
? ? ? ? 同向指針是雙指針的另一種核心形式,指兩個指針沿同一方向移動(如均從左到右),初始位置通常有先后關系(或起始于同一位置)
? ? ? ? 核心用途是在線性結構(如數組、鏈表)中進行原地元素篩選、位置調整或邊界劃分,無需依賴數據的有序性,更側重通過指針分工實現元素的 “有效區域” 與 “待處理區域” 分離
2. 移動邏輯
同向指針的核心是 “分工協作”:一個指針(通常稱為 “慢指針”)標記 “有效元素區域” 的邊界,另一個指針(通常稱為 “快指針”)負責遍歷所有元素并篩選目標元素,兩者同方向移動但節奏不同:
- 慢指針(slow):初始位置通常為序列起點(如索引 0)或特殊標記(如 - 1),僅當快指針找到 “有效元素” 時才移動,用于記錄 “已處理的有效元素” 的末尾位置;
- 快指針(fast):從序列起點開始,始終向前移動(如每次 + 1),負責遍歷所有元素,判斷當前元素是否符合 “有效” 條件(如非零、非目標值等)。
簡單說:快指針 “探路”,慢指針 “駐守有效區域”;快指針遇到有效元素時,慢指針 “接納” 并前移,遇到無效元素時,快指針獨自前行,慢指針保持不動。
3. 終止條件
循環終止于快指針遍歷完整個序列(如快指針到達數組末尾,即 fast == 序列長度)。此時慢指針的位置通常標記了 “有效元素區域” 的結束邊界(如慢指針索引 + 1 為有效元素的數量)。
4. 適用場景
同向指針的核心優勢是原地處理元素重排,且能保持有效元素的相對順序,適用于以下場景:
- 移動特定元素:如 “移動零”(將所有 0 移到末尾,非零元素保持順序);
- 移除元素:如 “移除數組中等于 val 的元素”(剩余元素保持相對順序);
- 壓縮序列:如 “刪除字符串中的所有相鄰重復項”“合并兩個有序數組(原地)” 等。
(二) 對撞指針(左右指針)
1. 定義與核心場景
? ? ? ? 對撞指針又稱 “左右指針”,其應用依賴于數據結構的有序性(如排序數組、對稱字符串),核心用途是高效查找滿足特定條件的元素或元素對,例如 “有序數組兩數之和”“驗證回文串”“反轉字符串”“刪除有序數組中的重復項(首尾驗證版)” 等問題。
2. 移動邏輯
指針初始位置分別位于線性結構的兩端,之后按照問題規則向中間同步逼近:
- 左指針(left):從序列最左端(索引 0 或起始位置)開始,每次向右側移動,一般為++left。
- 右指針(right):從序列最右端(索引 n-1 或末尾位置)開始,每次向左側移動,一般為--right。
3. 終止條件
終止時機需結合問題目標,核心分為兩類:
- 指針相遇或錯開:當無需提前匹配結果時,循環終止于left == right(兩指針指向同一位置,覆蓋所有元素)或left > right(兩指針交叉,遍歷完所有可能組合);
- 提前匹配終止:若在移動過程中找到滿足條件的結果(如nums[left] + nums[right] == target),可直接跳出循環,無需繼續逼近。
(三) 快慢指針(龜兔賽跑算法)
1. 定義與核心思想
? ? ? ? 快慢指針又稱 “龜兔賽跑算法”,其核心是讓兩個指針在同向移動的基礎上,保持不同的移動速度(如 “慢指針 1 步 / 次,快指針 2 步 / 次”)。通過速度差,可在無需額外空間的前提下,檢測序列的循環特性或定位特定位置。
2. 適用場景
快慢指針的核心優勢是處理 “循環相關” 或 “特定位置定位” 問題,常見場景包括:
- 環形結構檢測:如判斷鏈表是否有環、找到環形鏈表的入口;
- 特定位置定位:如查找鏈表的中間節點(用于歸并排序)、刪除鏈表的倒數第 k 個節點;
- 重復元素查找:如在無額外空間的要求下,找到數組中的重復元素(如 LeetCode 287. 尋找重復數)。
3. 常見實現方式
快慢指針的速度差可根據問題靈活調整,最經典的實現是 “1:2 速度比”:
- 慢指針(slow):每次移動 1 步(如slow = slow.next或slow += 1);
- 快指針(fast):每次移動 2 步(如fast = fast.next.next或fast += 2)。
原理類比:若序列存在環(如環形鏈表),快指針會像 “兔子” 一樣在環內循環,最終追上慢指針(“烏龜”);若序列無環(如普通鏈表),快指針會率先到達序列末尾(如鏈表的null節點),循環自然終止。
4. 其他變種實現
除了 “1:2 速度比”,快慢指針的速度差可根據目標調整:
- 定位鏈表倒數第 k 個節點:先讓快指針超前慢指針 k 步,再讓兩者同步移動(均 1 步 / 次);當快指針到達末尾時,慢指針恰好指向倒數第 k 個節點;
- 尋找數組中重復元素:讓慢指針按 “1 步 / 次” 移動,快指針按 “nums [fast] 步 / 次” 移動(模擬循環),最終兩指針會在重復元素位置相遇。
綜上,雙指針的選擇需結合問題的數據結構特性(有序 / 無序、線性 / 環形)和目標需求(查找 / 檢測 / 定位):若處理有序結構的元素查找,優先考慮對撞指針;若處理循環或特定位置問題,優先考慮快慢指針。
(三) 題目
題目1:移動零
鏈接:283. 移動零 - 力扣(LeetCode)
給定一個數組?nums,編寫一個函數將所有?0?移動到數組的末尾,同時保持非零元素的相對順序
請注意?,必須在不復制數組的情況下原地對數組進行操作。
核心思路:
該解法采用雙指針(同向指針)策略,通過兩個指針(dest和cur)劃分數組區間,實現零元素的移動:
1.先定義兩個指針——cur和dest
- cur:從左往右掃描數組,遍歷數組
- dest:已處理的區間內,非零元素的最后一個元素
此時三個區間:
- [0,dest] 非0區間
- [dest+1,cur-1] 0區間
- [cur,n-1] 待處理區間
cur遍歷時:
- 遇到0元素:cur++
- 遇到非0元素:交換dest+1和cur元素,再dest++,cur++
小思考:
為何是交換,不是直接覆蓋?
若直接覆蓋,在后面還得直接加0才可以,但是你怎么知道它要加多少個0會超級麻煩,而交換就讓非0元素全在左邊。0元素全在右邊,超級符合題目要求!
代碼:
class Solution {
public:void moveZeroes(vector<int>& nums) {for(int dest = -1, cur = 0; cur < nums.size(); cur++){if(nums[cur]){swap(nums[++dest],nums[cur]);}}}
};題目2:復寫0
鏈接:1089. 復寫零 - 力扣(LeetCode)
給你一個長度固定的整數數組?arr?,請你將該數組中出現的每個零都復寫一遍,并將其余的元素向右平移。
注意:請不要在超過該數組長度的位置寫入元素。請對輸入的數組?就地?進行上述修改,不要從函數返回任何東西。
核心思路:
該解法采用雙指針(同向指針)策略
1. 指針初始化——定義兩個指針 cur 和 dest
2. 定位最后一個復寫元素
結束條件:遍歷數組直至 cur 或 dest 超出有效范圍
遍歷規則:
- arr[cur]為0時dest走兩步
- arr[cur]部位0時dest走一步
3. 從后向前完成復寫操作
- arr[cur]為0時dest走兩步并且賦值成0
- arr[cur]部位0時dest走一步并拷貝cur的值
注意:邊界處理
針對如[1, 5, 0, 0, 6, 0, 8, 9]這類可能導致 dest 越界的情況:
核心——預先處理最后一次復寫
- 將 n-1 位置設為0
- 執行 cur-- 和 dest-=2 操作
代碼:
class Solution {
public:void duplicateZeros(vector<int>& arr) {int cur = 0, dest = -1, n = arr.size();while (cur < n){if (arr[cur])dest++;elsedest += 2;if (dest >= n - 1)break;cur++;}if (dest == n){arr[n - 1] = 0;cur--;dest -= 2;}while (cur >= 0){if (arr[cur])arr[dest--] = arr[cur--];else{arr[dest--] = 0;arr[dest--] = 0;cur--;}}
}
};題目3:快樂數
鏈接:202. 快樂數 - 力扣(LeetCode)
編寫一個算法來判斷一個數?n?是不是快樂數。
「快樂數」?定義為:
- 對于一個正整數,每一次將該數替換為它每個位置上的數字的平方和。
- 然后重復這個過程直到這個數變為 1,也可能是?無限循環?但始終變不到 1。
- 如果這個過程?結果為?1,那么這個數就是快樂數。
如果?n?是?快樂數?就返回?true?;不是,則返回?false?。
核心思路:
我們先來理解一下這個題目:
思路:
通過觀察圖片可以發現,這個問題可以類比鏈表的環檢測,因此采用雙指針(快慢指針)策略。
具體分析:
題目核心是判斷數組是否存在環,且環內元素為1(即環的起始元素為1)
實際上,所有數據都會形成環。根據鴿巢原理(n個鳥巢,n+1個鴿子,至少又一個鳥巢里面的鴿子數大于1):
- 最大數為2^31 - 1 ≈ 2.1×10^9
- 經過平方和運算后,結果范圍在[1,810]之間(9^2×10=810)
- 當任意數x運算超過811次時,必然出現重復值形成環
實現步驟:
- 定義快慢指針
- 快指針每次前進兩步,慢指針每次前進一步
- 判斷相遇時是否為1
注意事項: 雖然數字不是傳統意義上的指針,但在這個問題中可以將其視為指針來操作
代碼:
class Solution {
public:int bitSum(int n){int sum = 0;while(n){int a = n%10;sum += a*a;n/=10;}return sum;}bool isHappy(int n) {int slow = n, fast = bitSum(n);while(fast != slow){fast = bitSum(bitSum(fast));slow = bitSum(slow);}if(slow == 1)return true;elsereturn false;}
};
題目4:盛最多水的容器
鏈接:11. 盛最多水的容器 - 力扣(LeetCode)
給定一個長度為?n?的整數數組?height?。有?n?條垂線,第?i?條線的兩個端點是?(i, 0)?和?(i, height[i])?。
找出其中的兩條線,使得它們與?x?軸共同構成的容器可以容納最多的水。
返回容器可以儲存的最大水量。
說明:你不能傾斜容器。
核心思路:
1. 暴力解法
? ? ? ?設兩指針i?,?j,分別指向?槽板的最左端以及最右端,此時容器的寬度為 j - i?。由于容器的?度由兩板中的短板決定,因此可得容積公式:v = (j - i) * min(?height[i], height[j] )
? ? ? ? 但暴力解法需遍歷所有可能的(i, j)組合,時間復雜度為O(n2),會超出題目時間要求,因此需要優化。
2. 優化方法:雙指針(左右指針)策略(利用單調性)
采用左右指針初始分別指向數組兩端(left = 0,right = n-1),通過移動指針逐步縮小范圍,高效尋找最大容積。
步驟:
- 初始化左右指針left和right,計算當前容積并記錄為初始最大值;
- 比較 height[left] 和 height[right] 的大小,移動高度較小的一側指針(若相等,移動任意一側均可);
- 重新計算新指針位置的容積,更新最大值;
- 重復2和3,直到左右指針相遇,此時記錄的最大值即為結果。
移動較矮指針的原因:
假設當前height[left] < height[right](左邊界為短板):容器的寬度為 right - left
- 若移動右指針(較長的一側):新寬度必然減小(right-1 - left < right - left),且新的有效高度仍由左邊界決定(不會超過height[left]),因此容積一定會變小;
- 若移動左指針(較短的一側):雖然寬度減小,但可能遇到更高的左邊界,新的有效高度可能增大(最多等于右邊界高度),因此容積有可能變大。
同理,若height[right] < height[left],則應移動右指針。
這種策略通過放棄 “必然更小” 的可能,保留 “潛在更大” 的機會,將時間復雜度優化至O(n)。
代碼:
1.暴力解法:
//盛最多水的容器暴力解法
class Solution {
public:int maxArea(vector<int>& height) {int n = height.size();int ret = 0;for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){ret = max(ret, min(height[i], height[j]) * (j - i));}}return ret;}
};
2. 優化方法:雙指針策略(利用單調性)
//盛最多水的容器優化解法
class Solution {
public:int maxArea(vector<int>& height) {int left = 0, right = height.size() - 1, ret = 0;while (left < right){int v = min(height[left], height[right]) * (right - left);ret = max(ret, v);if (height[left] < height[right])++left;else--right;}return ret;}
};題目5:有效三角形的個數
鏈接:611. 有效三角形的個數 - 力扣(LeetCode)
給定一個包含非負整數的數組?nums?,返回其中可以組成三角形三條邊的三元組個數。
核心思路:
先來想想怎么判斷三個數是否構成三角形
核心條件是:任意兩邊之和大于第三邊。由于三角形中最長邊會限制另外兩邊的和(若最長邊小于另外兩邊之和,則其余兩邊的和必然大于第三邊),因此更高效的判斷方式是:最小的兩邊之和大于最長邊。
代碼思路:
1. 暴力解法
? ? ?先對數組排序(方便后續判斷大小關系),然后枚舉所有可能的三元組(i, j, k)(需滿足i < j < k),通過上述條件判斷是否能組成三角形。
? ? ?但這種方法需遍歷所有三元組,時間復雜度為O(n3),效率較低。
2. 優化方法:雙指針(左右指針)策略(利用單調性)
? ? ?核心邏輯:通過排序簡化大小判斷,固定最長邊后,用雙指針快速尋找符合條件的另外兩條邊,將時間復雜度降至O(n2)。
步驟:
1. 對數組排序(升序),便于利用 “最小兩邊之和> 最長邊” 的條件;
2. 固定最長邊:遍歷數組,設當前最長邊為nums[i](i從 2 開始,確保至少有兩個更小的數);
3. 初始化雙指針:
- 左指針left = 0(指向當前范圍內最小的數)
- 右指針right = i - 1(指向當前范圍內次大的數,即小于nums[i]的最大數)
4. 判斷與計數:
- 若nums[left] + nums[right] > nums[i]:由于數組遞增,left到right之間的所有數(nums[left], nums[left+1], ..., nums[right-1])都大于等于nums[left],因此它們與nums[right]的和必然也大于nums[i]。即此時left到right之間的所有數與nums[right]、nums[i]均可組成三角形,共有right - left個有效三元組,計入結果后將right左移(縮小范圍繼續尋找)
- 若nums[left] + nums[right] ≤ nums[i]:說明當前left對應的邊太小,需右移left(增大兩邊之和,嘗試滿足條件)
5. 重復步驟4,直到left >= right,再繼續固定下一個最長邊i。
代碼:
1. 暴力解法
//有效三角形的個數暴力解法
class Solution {
public:int triangleNumber(vector<int>& nums) {sort(nums.begin(), nums.end());int n = nums.size();int ret = 0;for (int i = 0; i < n; i++){for (int j = i + 1; j < n; j++){for (int k = j + 1; k < n; k++){if (nums[i] + nums[j] > nums[k])ret++;}}}return ret;}
};2. 優化方法:雙指針(左右指針)策略(利用單調性)
//有效三角形的個數優化解法
class Solution {
public:int triangleNumber(vector<int>& nums) {int n = nums.size() - 1;sort(nums.begin(), nums.end());int ret = 0;for (int i = n; i > 0; i--){int left = 0, right = i - 1;while (left < right){if (nums[left] + nums[right] > nums[i]){ret += (right - left);right--;}else{left++;}}}return ret;}
};題目6:查找總價格為目標值的兩個商品(和為s的兩個數字)
鏈接:LCR 179. 查找總價格為目標值的兩個商品 - 力扣(LeetCode)
購物車內的商品價格按照升序記錄于數組?price。請在購物車中找到兩個商品的價格總和剛好是?target。若存在多種情況,返回任一結果即可。
核心思路:
1. 暴力解法
? ? ? 定義兩個指針i和j(i < j),遍歷數組中所有可能的元素對,判斷price[i] + price[j]是否等于target。若找到符合條件的 pair,直接返回{price[i], price[j]}。
? ? ? 但此方法需枚舉所有組合,時間復雜度為O(n2),在數據量較大時效率較低。2.?優化方法:雙指針(左右指針)策略(利用單調性)
因數組是升序排列的,可通過雙指針快速縮小查找范圍,將時間復雜度降至O(n)。
步驟:
1. 初始化指針:左指針left指向數組起始位置(0),右指針right指向數組末尾(n-1);
2. 循環條件:當left < right時,持續判斷兩指針指向元素的和;
3. 具體判斷:
- 若price[left] + price[right] == target:找到目標組合,直接返回{price[left], price[right]};
- 若price[left] + price[right] < target:由于數組升序,right已指向當前范圍內最大的元素,此時和仍小于目標值,說明price[left]過小,需增大左側值,故將left右移(left++);
- 若price[left] + price[right] > target:同理,left已指向當前范圍內最小的元素,此時和仍大于目標值,說明price[right]過大,需減小右側值,故將right左移(right--)。
代碼:
1. 暴力解法
//和為s的兩個數字暴力解法
class Solution {
public:vector<int> twoSum(vector<int>& price, int target) {int n = price.size();for (int i = 0; i < n; i++){for (int j = i + 1; j < n; j++){if (price[i] + price[j] == target){return{ price[i],price[j] };}}}}
};2.?優化方法:雙指針(左右指針)策略(利用單調性)
//和為s的兩個數字優化解法
class Solution {
public:vector<int> twoSum(vector<int>& price, int target) {int left = 0, right = price.size() - 1;while (left < right){int sum = price[left] + price[right];if (sum == target){return { price[left], price[right] };}else if (sum > target)right--;elseleft++;}return { -1, -1 };}
};題目7:三數之和
鏈接:15. 三數之和 - 力扣(LeetCode)
給你一個整數數組?nums?,判斷是否存在三元組?[nums[i], nums[j], nums[k]]?滿足?i != j、i != k?且?j != k?,同時還滿足?nums[i] + nums[j] + nums[k] == 0?。請你返回所有和為?0?且不重復的三元組。
注意:答案中不可以包含重復的三元組。
核心思路:
1. 暴力解法
? ? ? 先對數組排序(為去重做準備),枚舉所有可能的三元組(i, j, k),要求i < j < k,判斷nums[i] + nums[j] + nums[k] == 0,若符合條件,將三元組加入結果集,同時通過跳過重復元素(相同值的i、j、k)避免重復三元組。
? ? ?但是三層循環的時間復雜度為O(n3),在數組長度較大時效率極低,無法滿足時間要求。2.?優化方法:雙指針(左右指針)策略(利用單調性)
利用排序后數組的單調性,將三層循環降為兩層,時間復雜度優化至O(n2),同時通過去重步驟確保結果不重復。
步驟:
1. 排序:對數組升序排序。排序的作用有二:一是使重復元素相鄰,便于去重;二是為雙指針移動提供單調性基礎。
2. 固定第一個數:遍歷數組,固定三元組的第一個數nums[i](i從 0 開始)。
- 若nums[i] > 0,由于數組升序,后續數均大于等于nums[i],三數之和必大于 0,可直接終止循環。
3. 雙指針找剩余兩數:在i右側的子數組[i+1, n-1]中,用左指針left = i+1、右指針right = n-1尋找滿足nums[left] + nums[right] = -nums[i]的組合:
- 若nums[left] + nums[right] < -nums[i]:需增大兩數之和,將left右移(利用升序特性,右側數更大);
- 若nums[left] + nums[right] > -nums[i]:需減小兩數之和,將right左移;
- 若相等:找到有效三元組,加入結果集。
4. 去重操作(關鍵):
- 固定數去重:當i > 0且nums[i] == nums[i-1]時,跳過當前i(避免重復固定相同的數,導致相同三元組);
- 雙指針針去重:找到有效三元組后,需同時將left右移、right左移,并跳過所有與當前left、right相同的元素(避免同一i下出現重復三元組)。
代碼:
1. 暴力解法
//三數之和暴力解法
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {vector<vector<int>> ret;sort(nums.begin(), nums.end());int n = nums.size();for (int i = 0; i < n; ){for (int j = i + 1; j < n; ){for (int k = j + 1; k < n; ){if (nums[i] + nums[j] + nums[k] == 0)ret.push_back({ nums[i],nums[j],nums[k] });k++;while (k < n && nums[k] == nums[k - 1])k++;}j++;while (j < n && nums[j] == nums[j - 1])j++;}i++;while (i < n && nums[i] == nums[i - 1])i++;}return ret;}
};2.?優化方法:雙指針(左右指針)策略(利用單調性)
//三數之和優化解法
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {vector<vector<int>> ret;sort(nums.begin(), nums.end());int n = nums.size();for (int i = 0; i < n; ){if (nums[i] > 0)break;int left = i + 1, right = n - 1;while (left < right){if (nums[left] + nums[right] == -nums[i]){ret.push_back({ nums[left], nums[right], nums[i] });left++;right--;while (left < right && nums[left] == nums[left-1])left++;while (left < right && nums[right] == nums[right+1])right--;}else if (nums[left] + nums[right] < -nums[i]){left++;}else {right--;}}i++;while(i < n && nums[i] == nums[i-1])i++;}return ret;}
}題目8:四數之和
鏈接:18. 四數之和 - 力扣(LeetCode)
給你一個由?n?個整數組成的數組?nums?,和一個目標值?target?。請你找出并返回滿足下述全部條件且不重復的四元組?[nums[a], nums[b], nums[c], nums[d]]?(若兩個四元組元素一一對應,則認為兩個四元組重復):
0 <= a, b, c, d?< na、b、c?和?d?互不相同nums[a] + nums[b] + nums[c] + nums[d] == target
你可以按?任意順序?返回答案 。
核心思路:
1. 暴力解法
? ? ? ?先對數組排序(為去重做準備);枚舉所有可能的四元組(i, j, k, z),要求i?< j?< k?< z,判斷nums[i] + nums[j] + nums[k] + nums[z] == target;若符合條件,將四元組加入結果集,同時通過跳過重復元素(相同值的a、b、c、d)避免重復四元組。
? ? ? ?但是四層循環的時間復雜度為O(n?),在數組長度較大時運算量極大,無法滿足時間要求。
2.?優化方法:雙指針(左右指針)策略(利用單調性)
利用排序后的單調性,通過 “固定兩個數 + 雙指針找剩余兩個數” 的方式,將四層循環降為三層,時間復雜度優化至O(n3),同時通過多層去重確保結果唯一。
步驟:
1. 排序預處理:對數組升序排序。排序的作用:一是使重復元素相鄰,便于后續去重;二是為雙指針移動提供單調性基礎,減少無效判斷。
2. 固定前兩個數:
- 第一層循環固定第一個數nums[i](i從 0 開始),若i?> 0且nums[i] == nums[i-1],則跳過當前i(去重,避免重復四元組);
- 第二層循環固定第二個數nums[j](j從i+1開始),若j?> i+1且nums[j] == nums[j-1],則跳過當前j(進一步去重)。
3. 雙指針找剩余兩數:在j右側的子數組[j+1, n-1]中,用左指針left = j+1、右指針right = n-1尋找滿足nums[left] + nums[right] == target - nums[i] - nums[j]的組合:
- 若nums[left] + nums[right] < 目標剩余和(即target - nums[i] - nums[j]):需增大兩數之和,將left右移(利用升序特性,右側數更大);
- 若nums[left] + nums[right] > 目標剩余和:需減小兩數之和,將right左移;
- 若nums[left] + nums[right] ==?目標剩余和:找到有效四元組,加入結果集,隨后同時將left右移、right左移,并跳過所有與當前left、right相同的元素(雙指針去重,避免同一i、j下出現重復四元組)。
代碼:
1. 暴力解法
1//四數之和暴力解法
class Solution {
public:vector<vector<int>> fourSum(vector<int>& nums, int target) {vector<vector<int>> ret;sort(nums.begin(), nums.end());int n = nums.size();for (int i = 0; i < n; i++){for (int j = i + 1; j < n; j++){for (int k = j + 1; k < n; k++){for (int z = k + 1; z < n; z++){if (nums[i] + nums[j] + nums[k] + nums[z] == target){ret.push_back({ nums[i],nums[j],nums[k],nums[z] });}}}}}return ret;}
};2.?優化方法:雙指針(左右指針)策略(利用單調性)
//四數之和優化解法
class Solution {
public:vector<vector<int>> fourSum(vector<int>& nums, int target) {vector<vector<int>> v;sort(nums.begin(), nums.end());int n = nums.size();for (int i = 0; i < n; ){for (int j = i + 1; j < n; ){int left = j + 1, right = n - 1;long long aim = (long long)target - nums[i] - nums[j];while (left < right){if (nums[left] + nums[right] == aim){v.push_back({ nums[i], nums[j], nums[left], nums[right] });left++;right--;while (left < right && nums[left] == nums[left - 1])left++;while (left < right && nums[right] == nums[right + 1])right--;}else if (nums[left] + nums[right] < aim)left++;elseright--;}j++;while (j < n && nums[j] == nums[j - 1])j++;}i++;while (i < n && nums[i] == nums[i - 1])i++;}return v;}
};博主的錯誤小記錄(這個是博主把這里當作直接的筆記了哈哈哈哈哈哈)
LeetCode出現超出時間是循環出現了問題!!!可以去調試!!!
以上就是算法之雙指針的學習就到這里告一段落,后續的完善工作我們將留待日后進行。希望這些知識能為你帶來幫助!如果覺得內容實用,歡迎點贊支持~ 若發現任何問題或有改進建議,也請隨時與我交流。感謝你的閱讀!
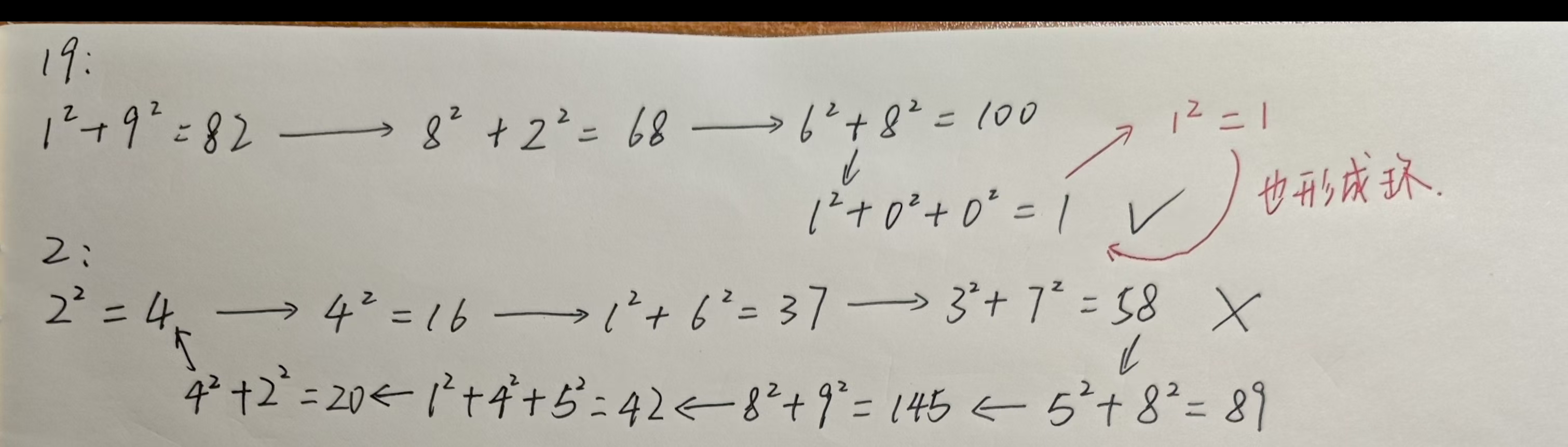




:RDD-Resilient Distributed Dataset)
)




)







)
