【數據結構——并查集】

引入

并查集（Disjoint Set Union，DSU）是一種用于管理元素分組的數據結構。

合并（Union）：將兩個不相交的集合合并為一個集合。
查找（Find）：確定某個元素屬于哪個集合，通常通過返回集合的“代表元素”（groupID或父節點）實現。

quickFind 和 quickUnion 是并查集的兩種實現方式。

每個元素初始時是一個獨立的集合，其groupID是本身下標或父節點指向自己（分別表明各自屬于哪個集合）。
如下：
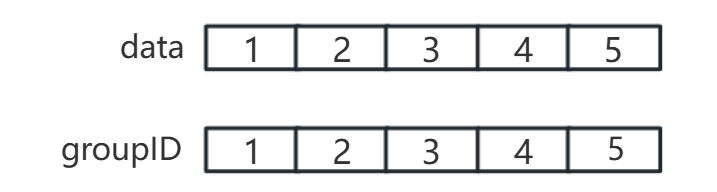
在這里插入圖片描述
主要就是對兩個數組所存的內容進行操作，特別是代表元素部分。
對代表元素進行操作的方向（思考角度）不同，就會使用不同的解決方案（如選擇quickFind還是quickUnion,）

quickFind

每個元素直接指向其所屬集合的代表元（根節點），合并操作時需要遍歷整個數組更新所有相關元素。

時間復雜度：
查找（Find）：O(1)，直接訪問數組即可確定所屬集合。
合并（Union）：O(n)，需要遍歷數組更新所有屬于同一集合的元素。

特點：查找速度快，但合并效率低（找快合慢）。

在這里插入圖片描述

頭文件

#pragma once
typedef int Element;typedef struct {Element* data;	 //存儲具體數據組編號int* groupID;    //存儲組編號int n;           //元素個數
}QuickFindSet;QuickFindSet* createQuickFindSet(int n);		//創建n個元素的quickFind樹（快查樹）
void releaseQuickFindSet(QuickFindSet* setQF);	//釋放setQF這個樹
void initQuickFindSet(const QuickFindSet* setQF, const Element* data, int n);//初始化setQF這個含n個結點的快查樹，以及data數組的值(groupID數組初始時常以下標為值,依次賦值就行了)
//查,判斷兩個元素是不是同一個組
int isSameQF(QuickFindSet* setQF, Element a, Element b);
//并，合并兩個元素
void unionQF(QuickFindSet* setQF, Element a, Element b);

功能實現

創建

QuickFindSet* createQuickFindSet(int n) {QuickFindSet* setQF = (QuickFindSet*)malloc(sizeof(QuickFindSet));if (setQF == NULL) {printf("setQF malloc failed!\n");return NULL;}//若申請成功，就傳遞n的值并繼續申請兩個數組的空間setQF->n = n;setQF->data =(Element*) malloc(sizeof(Element) * n);setQF->groupID = (int*)malloc(sizeof(int) * n);return setQF;
}

釋放

void releaseQuickFindSet(QuickFindSet* setQF) {if (setQF) {if (setQF->data) {free(setQF->data);}if (setQF->groupID) {free(setQF->groupID);}free(setQF);}
}

初始化

void initQuickFindSet(const QuickFindSet* setQF, const Element* data, int n) {for (int i = 0; i < n; ++i) {setQF->data[i] = data[i];setQF->groupID[i] = i;}
}

查找目標值的索引

static int findIndex(const QuickFindSet* setQF, Element e) {for (int i = 0; i < setQF->n; ++i) {if (setQF->data[i] == e) {return i;}}return -1;
}

判斷目標值索引對應的組ID是否相同(a、b在不在一個集合)

int isSameQF(QuickFindSet* setQF, Element a, Element b) {int aIndex = findIndex(setQF, a);int bIndex = findIndex(setQF, b);if (aIndex == -1 || bIndex == -1) {return 0;}return setQF->groupID[aIndex] == setQF->groupID[bIndex];
}

合并操作

void unionQF(QuickFindSet* setQF, Element a, Element b) {int aIndex = findIndex(setQF, a);int bIndex = findIndex(setQF, b);//假設把b集合中的元素合并到a集合上int gID = setQF->groupID[bIndex];		//先存下b的組號for (int i = 0; i < setQF->n; ++i) {if (setQF->groupID[i] == gID) {                 //是b組的元素setQF->groupID[i] = setQF->groupID[aIndex]; //全部組號改為a組的組號}}
}

功能調用

void test250808() {int n = 9;QuickFindSet* QFSet = createQuickFindSet(n);Element data[9];for (int i = 0; sizeof(data) / sizeof(data[0]); ++i) {data[i] = i;}initQuickFindSet(QFSet, data, n);unionQF(QFSet, 1, 3);unionQF(QFSet,3, 2);unionQF(QFSet, 2, 4);if (isSameQF(QFSet, 0, 2)) {printf("Yes\n");}else {printf("No\n");}unionQF(QFSet, 5, 1);if (isSameQF(QFSet, 5, 2)) {printf("Yes\n");}else {printf("No\n");}releaseQuickFindSet(QFSet);
}int main() {test250808();
}

quickUnion

使用樹結構表示集合(看下圖只能體現鏈式存儲，后面的內容會講到路徑壓縮：通過增大節點的度來提高效率會體現出樹的特點)，每個節點的parent指向其父節點，根節點
的parent指向自身,合并時將一個樹的根指向另一個樹的根就能連接兩個樹。

時間復雜度：
查找（Find）：O(logn)（平均，取決于樹高），需要遞歸或迭代找到根節點。
合并（Union）：O(logn)，僅需修改根節點的指向。

特點：合并效率高，但查找速度取決于樹高。

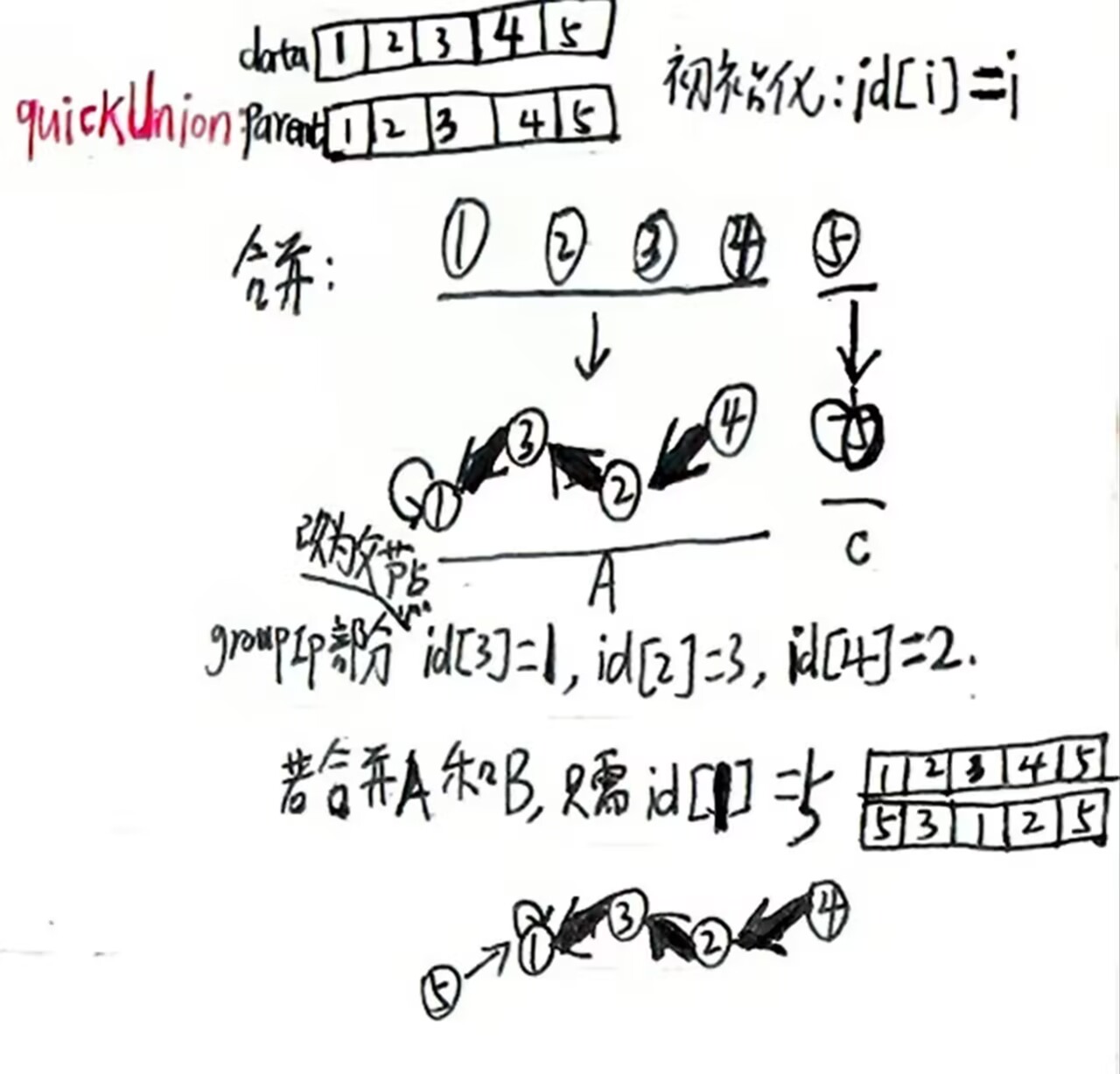
在這里插入圖片描述
這里是子節點指向父節點；父節點是自己時就指向自己，這種節點被稱為根節點（如1和5）。

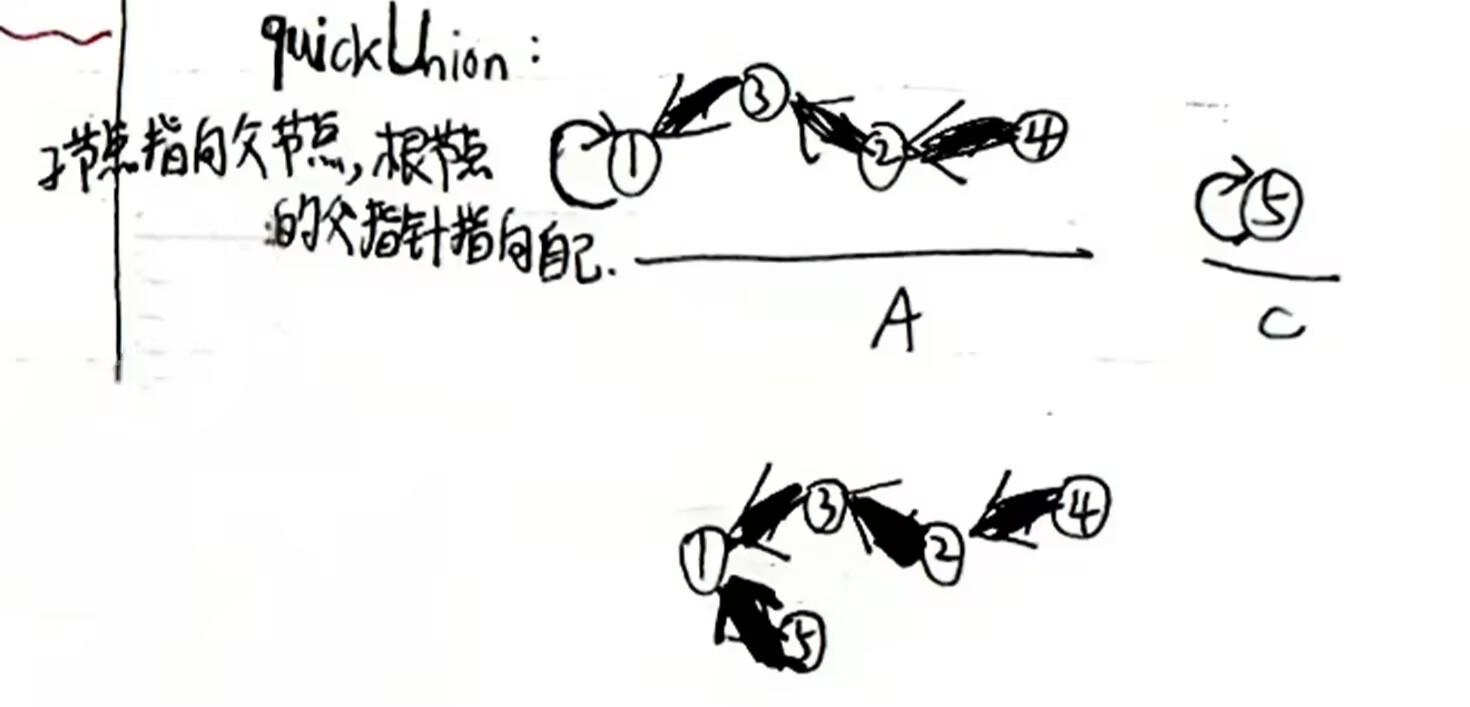
quickUnion查找速度取決于樹高,可通過路徑壓縮等進一步提升性能：

路徑壓縮

路徑壓縮就是想辦法把樹變矮。像上面的例子：從1到4這串右子樹，如果從根節點開始往下遍歷，將每個節點的parent都直接指向根節點1，當根節點查找目標節點時僅需訪問1層。

如何實現這一思想呢？遍歷這些節點以及將它們每個節點的parent指向根節點這一環節時，可以想象成從葉子節點開始挨個摘取并存下來（直接指向根節點的葉子節點忽略），遍歷到根節點時再挨個取出來并挨個將節點的parent指向根節點。

這種存儲特點就不由的聯想起了棧，相對提前申請空間的順序棧，鏈式棧更合適，用多少就申請多少。且需采用頭插法進行入棧操作（方便便利插入節點之后的節點元素）。
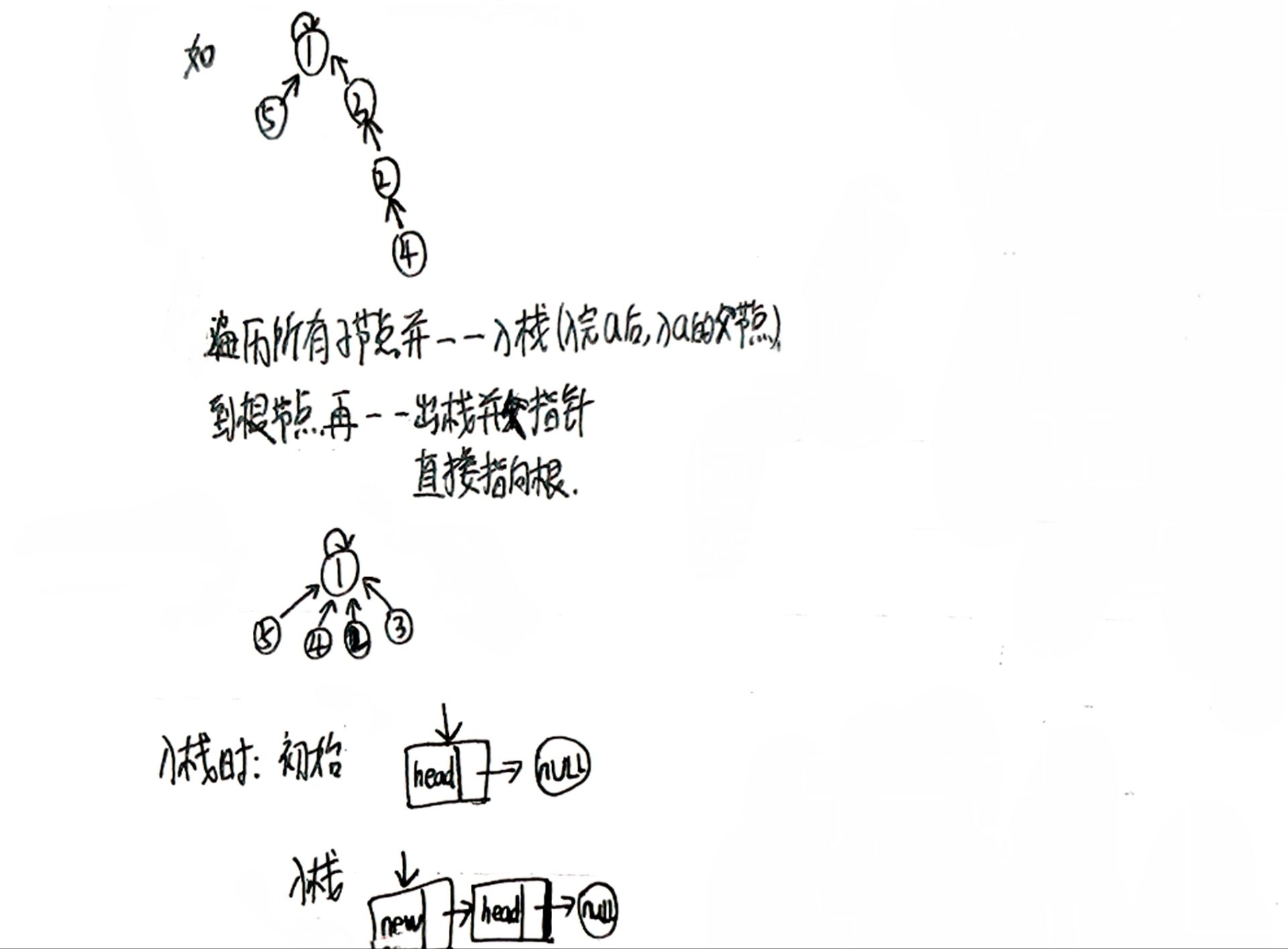
在這里插入圖片描述

與quickFind的代碼很相似，個別地方需調整。

頭文件

#pragma once
typedef int Element;typedef struct {Element* data;int* parent;int* size;  //表示其中某個集合的元素個數int n;		//表示總元素個數（所有集合的元素個數之和）
}QuickUnionSet;//為壓縮存儲中鏈式棧的入棧出棧操作做準備:定義節點結構
typedef struct _set_node {int index;struct _set_node* next;
}SetNode;QuickUnionSet* createQuickUnionSet(int n);
void releaseQuickUnionSet(QuickUnionSet* setQU);
void initQuickUnionSet(QuickUnionSet* setQU, const Element* data, int n);int isSameQU(const QuickUnionSet* setQU, Element a, Element b);
void unionQU(QuickUnionSet* setQU, Element a, Element b);

功能實現

創建

QuickUnionSet* createQuickUnionSet(int n) {QuickUnionSet* setQU = (QuickUnionSet*)malloc(sizeof(Element) * n);if (setQU == NULL) {return NULL;}setQU->data = (Element*)malloc(sizeof(Element) * n);setQU->parent = (int*)malloc(sizeof(int) * n);setQU->size = (int*)malloc(sizeof(int) * n);setQU->n = n;return setQU;
}

釋放

void releaseQuickUnionSet(QuickUnionSet* setQU) {if (setQU) {if (setQU->data) {free(setQU->data);}if (setQU->parent) {free(setQU->parent);}if (setQU->size) {free(setQU->size);}}
}

初始化

void initQuickUnionSet(QuickUnionSet* setQU, const Element* data, int n) {for (int i = 0; i < n; i++) {setQU->data[i] = data[i];setQU->parent[i] = i;setQU->size[i] = 1;}
}

查找目標值索引

static int findIndex(const QuickUnionSet* setQU, Element e) {for(int i = 0; i < setQU->n; ++i) {if (setQU->data[i] == e) {return i;}}return -1;
}

路徑壓縮

#define PATH_COMPRESS
#ifndef PATH_COMPRESS
static int findRootIndex(const QuickUnionSet* setQU, Element e) {int curIndex = findIndex(setQU, e);if (curIndex == -1) {return -1;}
//若找到則向上遍歷，直到父節點和自身索引一致（找到根節點）while(setQU->parent[curIndex]!=curIndex) {curIndex = setQU->parent[curIndex];}return curIndex;
}
#else
static SetNode* push(SetNode* stack, int index) {
//傳入的stack是一個空指針，相當于無頭結點、頭指針鏈式結構的頭插操作SetNode* node = (SetNode*)malloc(sizeof(SetNode));node->index = index;node->next = stack;return node;
}static SetNode* pop(SetNode* stack, int* index) {SetNode* tmp = stack;
//主要任務是獲得棧頂元素的索引*index = stack->index;//之后更新棧頂索引stack = stack->next;free(tmp);return stack;
}static int findRootIndex(const QuickUnionSet* setQU, Element e) {int curIndex = findIndex(setQU, e);if (curIndex == -1)return -1;
//找根的路徑：從目標節點開始往上找，途經的節點都挨個入棧，到根節點為止SetNode* path = NULL;while (setQU->parent[curIndex] != curIndex) {path = push(path, curIndex);curIndex = setQU->parent[curIndex];}
//出棧，并將出棧的每個節點的parent都指向根節點while (path) {int pos;path = pop(path, &pos);setQU->parent[pos] = curIndex;}return curIndex;
}
#endif // !PATH_COMPRESS

判斷兩集合根的異同

int isSameQU(const QuickUnionSet* setQU, Element a, Element b) {int aRoot = findRootIndex(setQU, a);int bRoot = findRootIndex(setQU, b);if (aRoot == -1 || bRoot == -1) {return 0;}return aRoot == bRoot;
}

合并

/* 將元素a和元素b進行合并* 1. 找到a和b的根節點，原本是b的父節點指向a的父節點* 2. 引入根節點的size有效規則，誰的元素多，讓另外一個接入元素多的組*/void unionQU(QuickUnionSet* setQU, Element a, Element b) {int aRoot = findRootIndex(setQU, a);int bRoot = findRootIndex(setQU, b);if (aRoot == -1 || bRoot == -1) {return;}if (aRoot != bRoot) {    // a和b不在一個集合里
// 根據根節點的索引找到對應size空間里保存的根所在樹的總節點數//初始時size都為1,節點都是單獨占一個集合,結合時再將兩集合的size相加int aSize = setQU->size[aRoot];int bSize = setQU->size[bRoot];if (aSize >= bSize) {	// 將b元素的根節點指向a元素的根節點setQU->parent[bRoot] = aRoot;setQU->size[aRoot] += bSize;}else {setQU->parent[aRoot] = bRoot;setQU->size[bRoot] += aSize;}}
}

功能調用

void test250810() {int n = 9;QuickUnionSet* QUSet = createQuickUnionSet(n);Element data[9];for (int i = 0; i < sizeof(data) / sizeof(data[0]); ++i) {data[i] = i;}initQuickUnionSet(QUSet, data, n);unionQU(QUSet,1, 3);unionQU(QUSet, 3, 2);unionQU(QUSet, 2, 4);if (isSameQU(QUSet, 0, 2)) {printf("Yes\n");}else {printf("No\n");}unionQU(QUSet, 5, 1);if (isSameQU(QUSet, 5, 2)) {printf("Yes\n");}else {printf("No\n");}releaseQuickUnionSet(QUSet);
}
int main() {test250810();
}