前言
參考了以下大佬的博客
https://blog.csdn.net/v_july_v/article/details/127411638
https://blog.csdn.net/andy_shenzl/article/details/140146699
https://blog.csdn.net/weixin_42475060/article/details/121101749
https://blog.csdn.net/weixin_43334693/article/details/130189238
https://blog.csdn.net/weixin_42110638/article/details/134016569
https://www.cnblogs.com/nickchen121/p/16470569.html
非常感謝!
Seq2Seq
定義
Seq2Seq是一個Encoder-Decoder結構的網絡,它的輸入是一個序列,輸出也是一個序列,
Encoder使用循環神經網絡(RNN,GRU,LSTM等),將一個可變長度的信號序列(輸入句子)變為固定維度的向量編碼表達,
Decoder使用循環神經網絡(RNN,GRU,LSTM等),將這個固定長度的編碼變成可變長度的目標信號序列(生成目標語言)
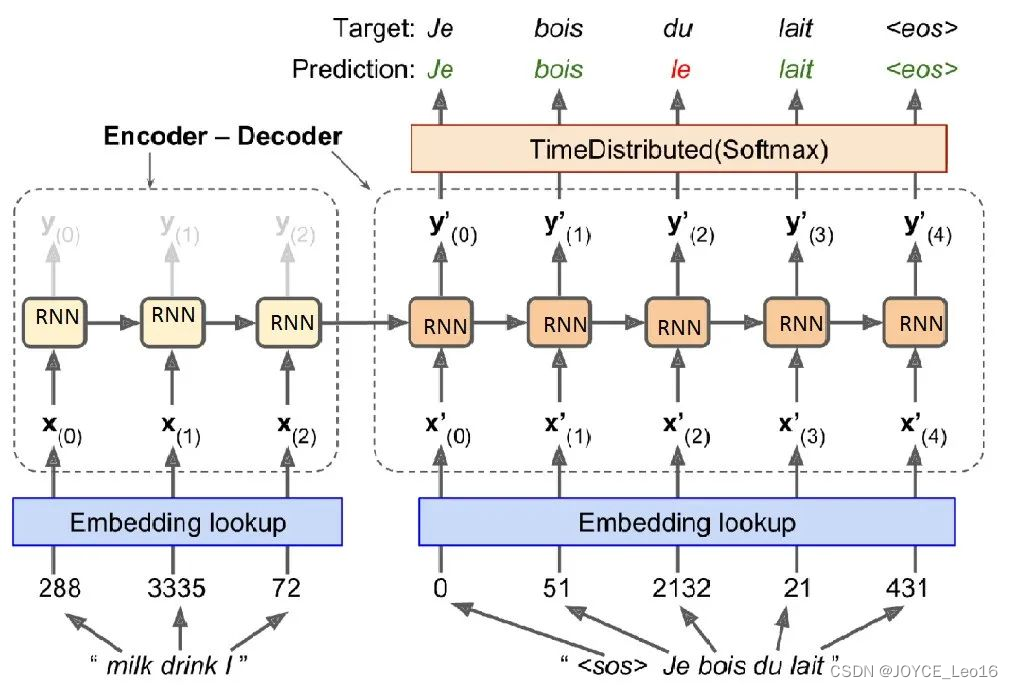
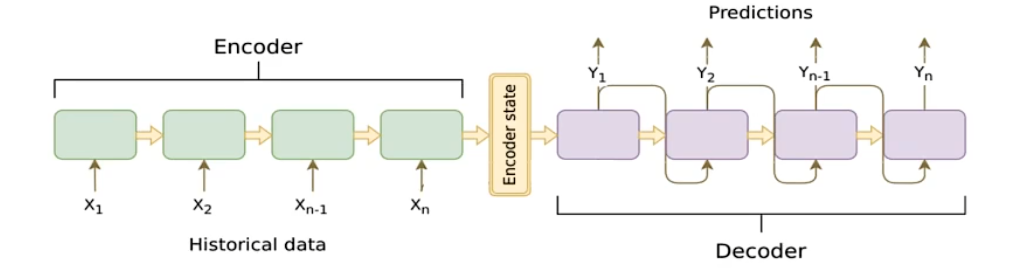
圖中的圓角矩形即為cell:可以是RNN,GRU,LSTM等結構
- 相當于將
RNN中的h0h_0h0?輸入Encoder(將Decoder部分理解成RNN,Encoder輸出的Encoder state作為h0h_0h0?)
Seq2Seq模型通過 端到端(?) 的訓練方式,將輸入序列和目標序列直接關聯起來,避免了傳統方法中繁瑣的特征工程和手工設計的對齊步驟。這使得模型能夠自動學習從輸入到輸出的映射關系,提高了序列轉換任務的性能和效率
端到端(End-to-End Learning)
如何理解這個端到端(End-to-End Learning)?
輸入序列到輸出序列的全過程都由模型學習,我們不需要進行設計規則或特征
工作原理
Seq2Seq中的編碼器使用循環神經網絡將輸入序列轉換為固定維度的上下文向量,而解碼器使用這個向量和另一個循環神經網絡逐步生成輸出序列
編解碼器
編碼器Encoder
把一個不定長的輸入序列x1,??,xtx_1,\cdots,x_tx1?,?,xt?輸出到一個編碼狀態CCC
- 編碼過程中,編碼器會逐個讀取輸入序列的元素,并更新其內部隱藏狀態
- 編碼完成后,編碼器將最后一個輸出的隱藏狀態或經過某種變換的隱藏狀態作為上下文向量/編碼狀態傳遞給解碼器
解碼器Decoder
輸出yty^tyt的條件概率將基于之前的輸出序列y1,??,yt?1y^1,\cdots,y^{t-1}y1,?,yt?1和編碼器輸出的編碼狀態CCC
- 在每個時間步ttt上,解碼器將根據上一個時間步的輸出yt?1y^{t-1}yt?1,當前隱藏狀態以及編碼狀態C編碼狀態C編碼狀態C來生成當前時間步輸出yty^tyt
作用
對于給定的輸入序列x1,??,xt,??,xTx_1,\cdots,x_t,\cdots,x_Tx1?,?,xt?,?,xT?,使輸出序列y1,??,yt′,??,yT′y^1,\cdots,y^{t'},\cdots,y^{T'}y1,?,yt′,?,yT′的條件概率值最大
就相當于求:
argmax(P(y1,??,??,yT′∣x1,??,xT))
\begin{align}
argmax(P(y^1,\cdots,\cdots,y^{T'}|x_1,\cdots,x_T))
\end{align}
argmax(P(y1,?,?,yT′∣x1?,?,xT?))??
得到一組使條件概率最大的輸出序列y1,??,yt′,??,yT′y^1,\cdots,y^{t'},\cdots,y^{T'}y1,?,yt′,?,yT′
最大似然估計
對于上面的做法,我們要使用最大似然估計來求出使得條件概率最大的輸出序列y1,??,yt′,??,yT′y^1,\cdots,y^{t'},\cdots,y^{T'}y1,?,yt′,?,yT′
由于解碼器的時間步輸出值由前面的時間步輸出以及當前時間步隱藏狀態和編碼狀態C共同決定
最大似然估計為:
P(y1,??,??,yT′∣x1,??,xT)=∏t′=1T′P(yt′∣y1,??,yt′?1,C)
P(y^1,\cdots,\cdots,y^{T'}|x_1,\cdots,x_T) = \prod_{t'=1}^{T'}P(y^{t'}|y^1,\cdots,y^{t'-1},C)
P(y1,?,?,yT′∣x1?,?,xT?)=t′=1∏T′?P(yt′∣y1,?,yt′?1,C)
多個概率連乘,最后的值會很小,不利于存儲,進行取對數操作
logP(y1,??,??,yT′∣x1,??,xT)=∑t′=1T′logP(yt′∣y1,??,yt′?1,C) logP(y^1,\cdots,\cdots,y^{T'}|x_1,\cdots,x_T) = \sum_{t'=1}^{T'}logP(y^{t'}|y^1,\cdots,y^{t'-1},C) logP(y1,?,?,yT′∣x1?,?,xT?)=t′=1∑T′?logP(yt′∣y1,?,yt′?1,C)
轉換為使每個yt′y^{t'}yt′的條件概率最大的問題,最終得到最優的輸出序列
注意力機制Attention Mechanism
核心邏輯
從關注全部到關注重點
- Attention機制處理長文本時,能夠抓住重點,不丟失重要信息
- Attention機制類似于人類看圖片的邏輯,會將注意力放在圖片的焦點上
怎么做注意力
例子

比如對于這張圖片,紅色部分是人們更關注的
人看這張圖片的過程可以描述為:人(查詢對象Q(Query))看這張圖片(被查詢對象V(Values)),判斷圖片中哪些信息更重要,哪些信息更不重要(計算Q和V里事物的重要度(相關程度))
相似度計算
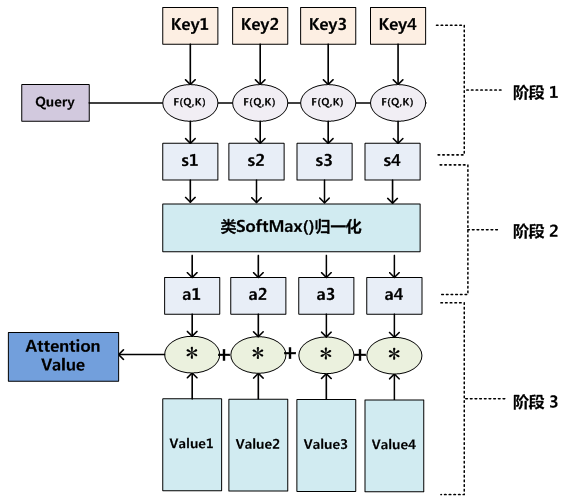
K (Key):與Q匹配的鍵,通過計算Q和K的相似度來得到注意力權重
類比:
- Q:用戶的搜索請求,比如搜索科幻電影
- K:所有電影標簽
- V:電影本身內容
計算Q與K的相似度,得到權重向量,最終與V加權求和
方法
使用點乘的形式計算相似度(i=1,2,...,n)(i=1,2,...,n)(i=1,2,...,n)
f(Q,Ki)=QT?Ki \begin{align} f(Q,K_i) = Q^T\cdot K_i \end{align} f(Q,Ki?)=QT?Ki???
感知器
f(Q,Ki)=vTTanh(W?Q+U?Ki)v,W,U:可學習的參數矩陣
\begin{align}
f(Q,K_i) = v^TTanh(W\cdot Q+U \cdot K_i)\\
v,W,U:可學習的參數矩陣\\
\end{align}
f(Q,Ki?)=vTTanh(W?Q+U?Ki?)v,W,U:可學習的參數矩陣??
權重點乘
f(Q,Ki)=Q?W?KiW:可學習的參數矩陣 \begin{align} f(Q,K_i) = Q\cdot W \cdot K_i \\ W:可學習的參數矩陣 \end{align} f(Q,Ki?)=Q?W?Ki?W:可學習的參數矩陣??
權重拼接
f(Q,Ki)=W[Q;Ki]將Q和K向量拼接在一起,通過可學習參數矩陣W做線性變化 \begin{align} f(Q,K_i) = W[Q;K_i] \\ 將Q和K向量拼接在一起,通過可學習參數矩陣W做線性變化 \end{align} f(Q,Ki?)=W[Q;Ki?]將Q和K向量拼接在一起,通過可學習參數矩陣W做線性變化??
softMax+歸一化
αi=softMax(f(Q,Ki)dk)dk:縮放因子,是Query向量和K向量的維度
\begin{align}
\alpha_i = softMax(\frac{f(Q,K_i)}{\sqrt{d_k}})\\
d_k:縮放因子,是Query向量和K向量的維度
\end{align}
αi?=softMax(dk??f(Q,Ki?)?)dk?:縮放因子,是Query向量和K向量的維度??
為什么要除以一個dk\sqrt{d_k}dk??(?)
假設Q,K的每個元素是獨立隨機變量,均值為0,方差為1,那么點乘操作之后,均值為0,每個元素的方差為Q和K的維度dkd_kdk?
當dkd_kdk?很大時,分布就會集中在絕對值大的區域,造成概率兩極化(接近0/1),造成梯度消失
加權求和
針對計算出的αi,對V中所有的value進行加權求和,得到Attention向量:針對計算出的\alpha_i,對V中所有的value進行加權求和,得到Attention向量:針對計算出的αi?,對V中所有的value進行加權求和,得到Attention向量:
Attention(Q,K,V)=∑i=1nαi?Vi=∑i=1nsoftMax(f(Q,Ki)dk)?Vi \begin{align} Attention(Q,K,V) = \sum_{i=1}^{n} \alpha_i \cdot V_i = \sum_{i=1}^{n} softMax(\frac{f(Q,K_i)}{\sqrt{d_k}}) \cdot V_i \end{align} Attention(Q,K,V)=i=1∑n?αi??Vi?=i=1∑n?softMax(dk??f(Q,Ki?)?)?Vi???
seq2seq with Attention
在傳統的seq2seq中有一個顯著的缺點:
長句子問題
最初引入注意力機制是為了解決機器翻譯中遇到的長句子(超過50字)性能下降問題
傳統的機器翻譯在長句子上的效果并不理想,本質原因是:
在Encoder-Decoder結構中,Encoder會將輸入序列中的所有詞統一編碼成一個語義特征C后,再進行解碼;因此C中就包含了輸入序列的所有信息,它的長度就成了限制性能的瓶頸。對于長句子,語義特征C可能并不能存下所有的信息,造成了效果不佳
結構
在最初的seq2seq中,結構為
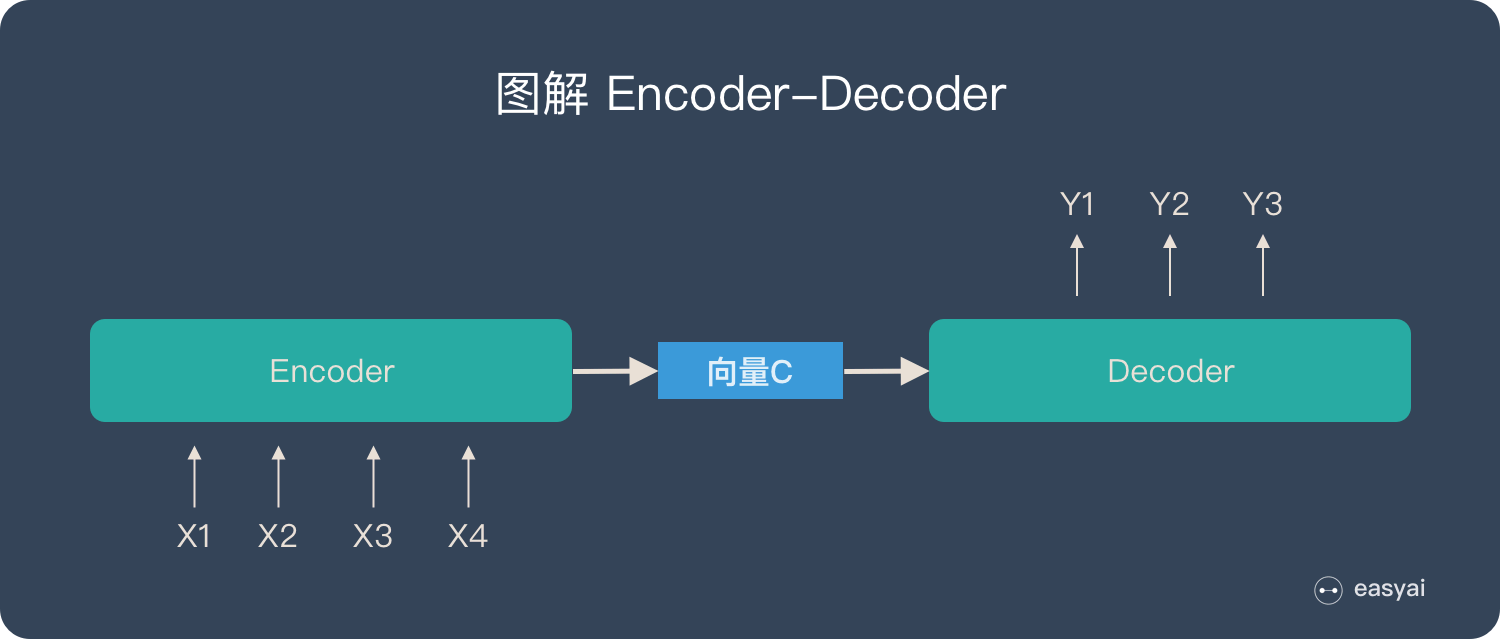
整個輸入序列被編碼為一個固定長度的編碼狀態C
而引入Attention機制之后,整個輸入序列不再被編碼成一個定長的編碼狀態C,而是編碼成一個向量序列C=[C1,??,Cn]C=[C_1,\cdots,C_n]C=[C1?,?,Cn?]
核心在于:Ci根據輸出生成單詞yi不斷變化C_i根據輸出生成單詞y_i不斷變化Ci?根據輸出生成單詞yi?不斷變化
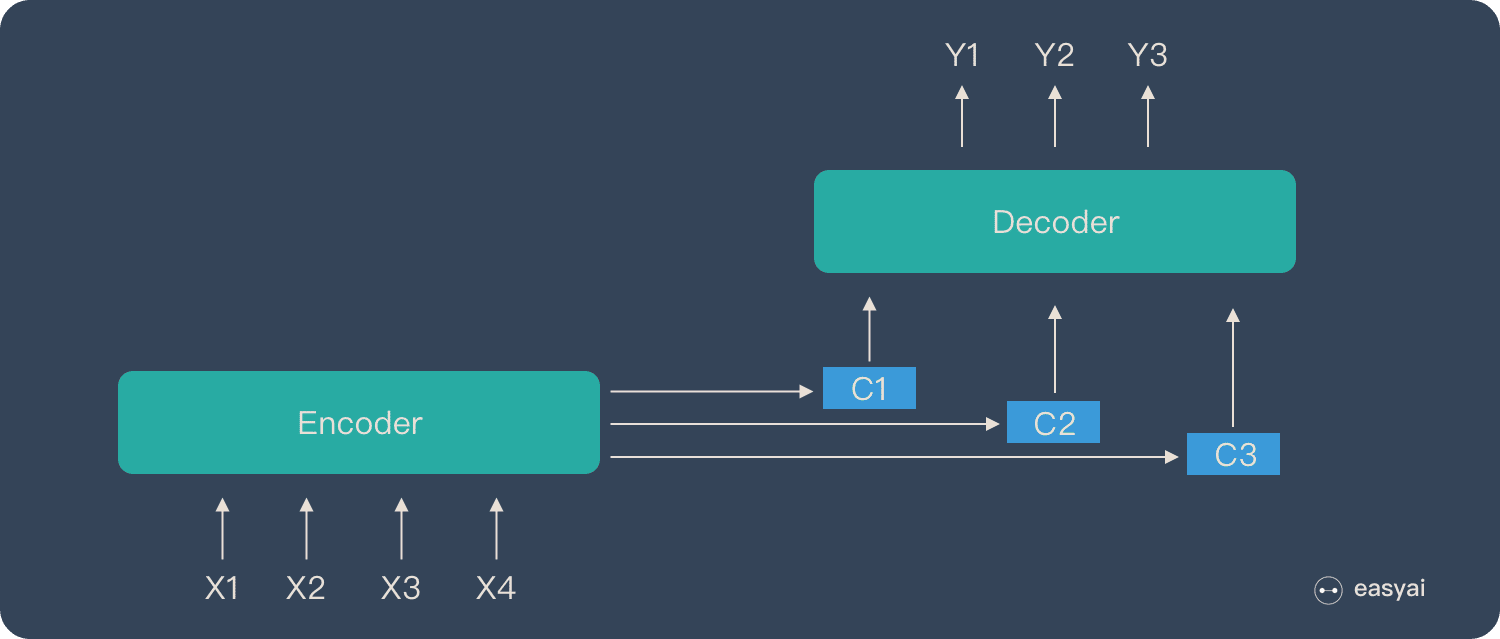
從解碼器輸出的角度:
- 每個輸出詞y都會受到每個輸入詞x1,x2,x3,x4的影響,但是每個輸入詞對最終輸出詞y的影響權重不一樣,這個權重由Attention計算得到
工作原理
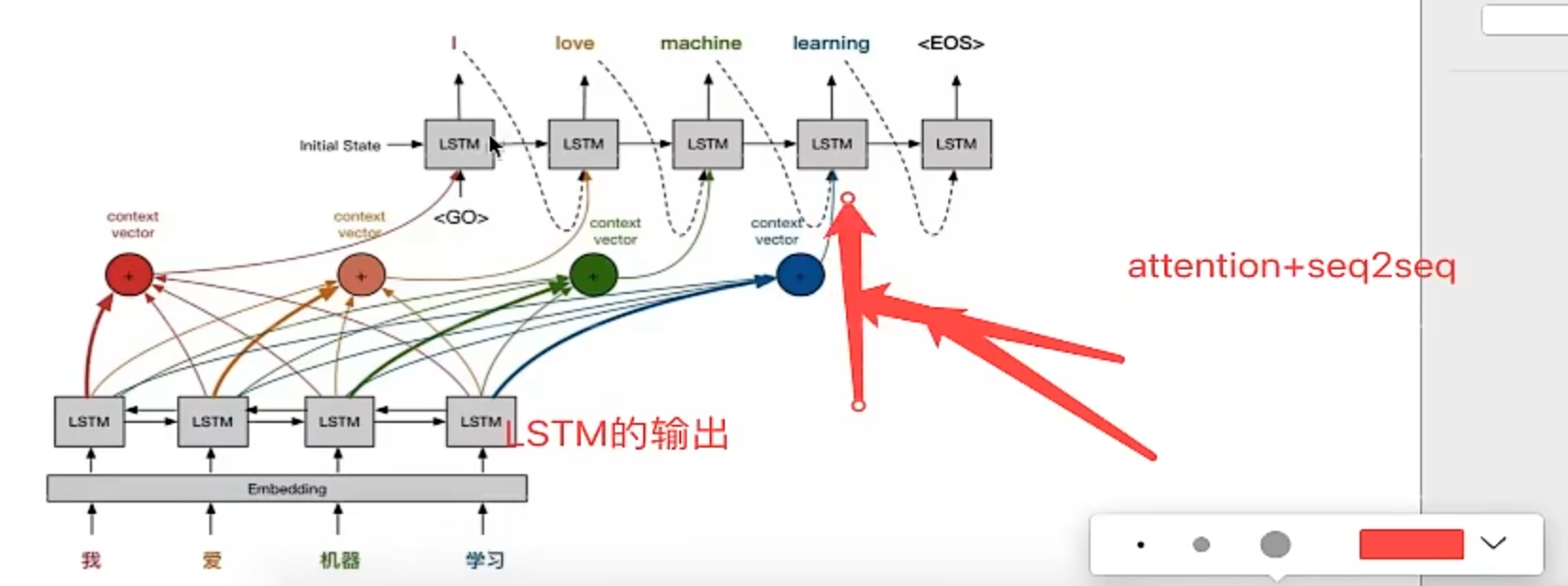
此時Decodert時刻有3個輸入: t-1時刻的隱藏狀態輸出和循環神經網絡輸出,以及Encoder輸出的context-vec
編碼器Encoder
結構
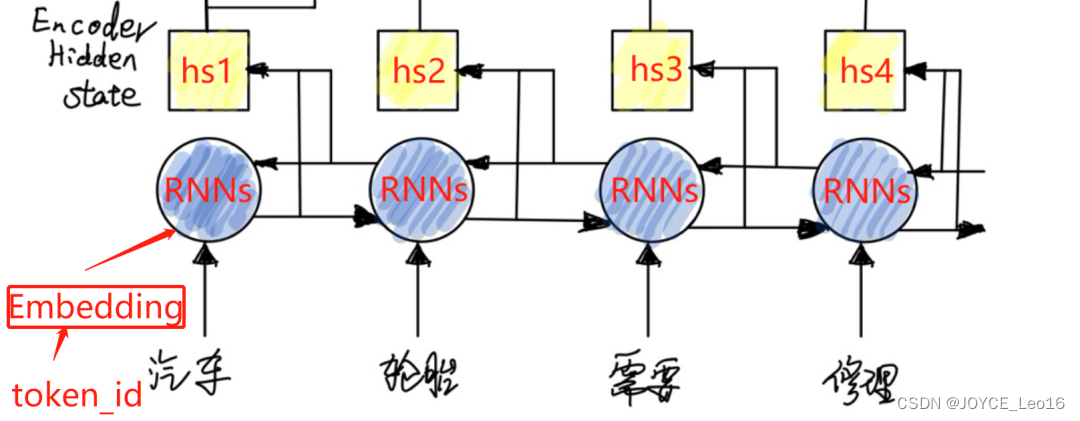
雙向循環神經網絡
在Seq2Seq with Attention的編碼器中,使用了雙向的RNN,GRU,LSTM結構,簡稱為RNNs
雙向RNNs(BiRNNs)由前向RNNs和后向RNNs,分別處理序列前半部分和后半部分
比如對于"I love deep-learning",通過BiRNNs可以同時知道love前面是I,后面是deep-learning
流程
- 輸入處理
- 將語料分詞后的
token_id分批次傳入embedding層,轉換為詞向量(Word2Vec形式,one-hot形式…)
什么是token-id(?)
就是分詞后的單詞在詞庫V中對應的唯一整數索引
- 將語料分詞后的
- 特征提取
- 將前一步得到的詞向量作為輸入,傳入
Encoder的特征提取器-使用BiRNNs
- 將前一步得到的詞向量作為輸入,傳入
- 狀態輸出
- 兩個方向的RNNs都會產生隱藏狀態輸出,將這兩個隱藏狀態輸出拼接,作為1個完整的隱藏狀態輸出h
解碼器Decoder
結構
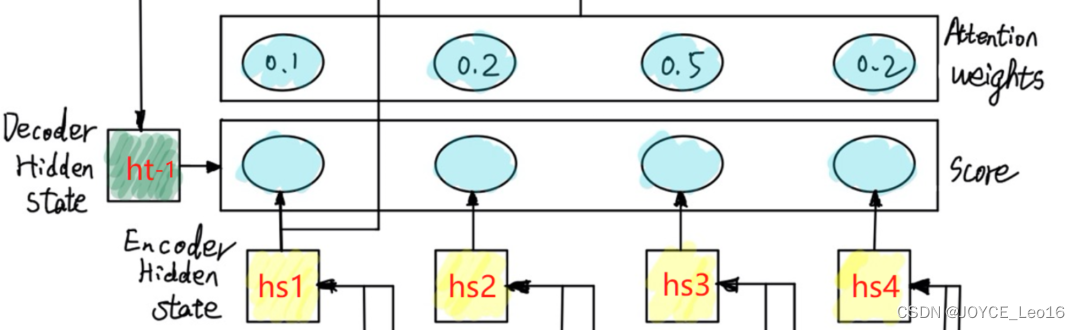
流程
- 隱藏狀態
- 前一時刻的隱藏狀態輸出st?1s_{t-1}st?1?
- 計算相似度score
- 計算前一時刻隱藏狀態輸出st?1s_{t-1}st?1?與Encoder的第j步隱藏狀態輸出hjh_jhj?的相似度score
- 計算注意力權重
- 將上一步的相似度score進行softMax歸一化
計算上下文向量Context Vec
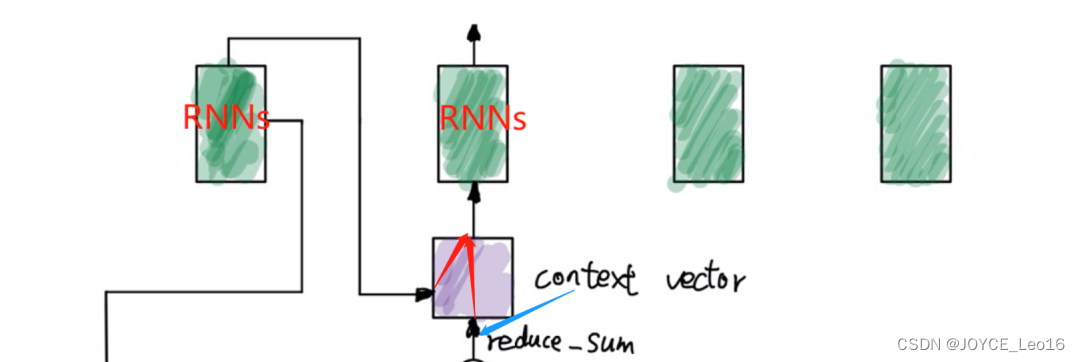
得到的hj與權重αij進行加權求和,得到上下文向量 得到的h_j與權重\alpha_{ij}進行加權求和,得到上下文向量 得到的hj?與權重αij?進行加權求和,得到上下文向量
公式
注意力分數計算
使用Decoder前一時刻隱藏狀態st?1s_{t-1}st?1?,Encoder中第j個時間步的隱藏狀態hjh_jhj?,進行計算得到注意力權重αij\alpha_{ij}αij?
計算匹配得分
匹配得分eij表示Decoder在第i?1步的隱藏狀態輸出si?1,與Encoder在第j步的隱藏狀態輸出hj之間的匹配程度 匹配得分e_{ij}表示Decoder在第i-1步的隱藏狀態輸出s_{i-1},與Encoder在第j步的隱藏狀態輸出h_j之間的匹配程度 匹配得分eij?表示Decoder在第i?1步的隱藏狀態輸出si?1?,與Encoder在第j步的隱藏狀態輸出hj?之間的匹配程度
- 方法1:感知器
eij=vT?Tanh(W?si?1+U?hj) \begin{align} e_{ij} = v^T\cdot Tanh(W\cdot s_{i-1} + U\cdot h_j) \end{align} eij?=vT?Tanh(W?si?1?+U?hj?)?? - 方法2:使用二次型矩陣計算
二次型:一個向量和矩陣的乘積
eij=si?1?Wi?1,j?hj e_{ij} = s_{i-1}\cdot W_{i-1,j} \cdot h_j eij?=si?1??Wi?1,j??hj?
計算權重 αij\alpha_{ij}αij?:
使用softMax函數進行歸一化
αij=eij∑i=1neik \alpha_{ij} = \frac{e_{ij}}{\sum_{i=1}^{n}e_{ik}} αij?=∑i=1n?eik?eij??
計算上下文向量 Context Vec
Ci=∑j=1nαij?hjn:序列長度Ci:解碼步驟i的上下文向量αij:輸入序列中第j個詞對解碼步驟i的注意力權重hj:編碼器輸出的第j個詞的隱藏狀態 \begin{align} C_i = \sum_{j=1}^{n}\alpha_{ij}\cdot h_j \\ n:序列長度\\ C_i:解碼步驟i的上下文向量\\ \alpha_{ij}:輸入序列中第j個詞對解碼步驟i的注意力權重\\ h_j:編碼器輸出的第j個詞的隱藏狀態\\ \end{align} Ci?=j=1∑n?αij??hj?n:序列長度Ci?:解碼步驟i的上下文向量αij?:輸入序列中第j個詞對解碼步驟i的注意力權重hj?:編碼器輸出的第j個詞的隱藏狀態??
比如對于"我 愛 機器 學習" -> "I love machine learning"這個翻譯過程
對于i=1,就是要計算 "I" 與 "我","愛","機器","學習" 每個時刻輸入的相關性
類別
自注意力機制Self Attention
Self-Attention的關鍵點:Q,K,V都是來源于同一個序列X,通過X找到X里面的關鍵點
架構
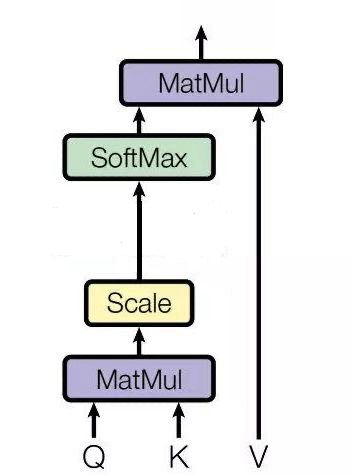
Self-Attention 有3個輸入 Q,K,V:
這三個輸入來源于同一個輸入序列X的詞向量x的線性變換
定義三個可學習的參數矩陣:WQ,WK,WVW_Q,W_K,W_VWQ?,WK?,WV?
Q,K,V定義如下:
Q=x?WQK=x?WKV=x?WV
\begin{align}
Q = x \cdot W_Q\\
K = x\cdot W_K \\
V = x\cdot W_V
\end{align}
Q=x?WQ?K=x?WK?V=x?WV???
流程
先以向量為例子:
-
得到初始的
Q,K,V
對于序列X中第i個單詞Xi的詞向量xi??(i?∈(0,n]):Qi=xi?WQKi=xi?WKVi=xi?WV \begin{align} 對于序列X中第i個單詞X_i的詞向量x_i\ \ (i \ \in (0,n]):\\ Q_i = x_i \cdot W_Q\\ K_i = x_i \cdot W_K\\ V_i = x_i \cdot W_V\\ \end{align} 對于序列X中第i個單詞Xi?的詞向量xi???(i?∈(0,n]):Qi?=xi??WQ?Ki?=xi??WK?Vi?=xi??WV???
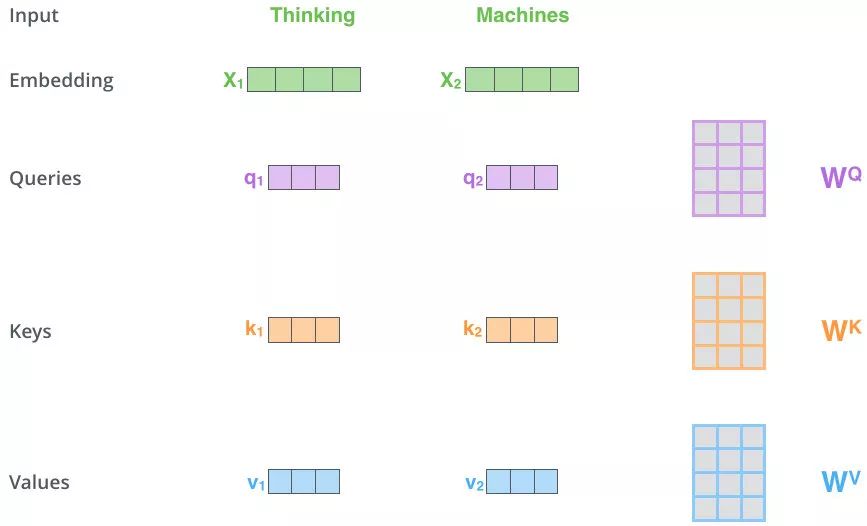
-
計算當前查詢Qi與其他Kj(包括當前Qi對應的Ki)的相似度計算當前查詢Q_i與其他K_j(包括當前Q_i對應的K_i)的相似度計算當前查詢Qi?與其他Kj?(包括當前Qi?對應的Ki?)的相似度
使用點乘計算相似度:sij=Qi?Kj???(i,j?∈[0,n]) \begin{align} 使用點乘計算相似度:\\ s_{ij} = Q_i \cdot K_j\ \ \ (i,j\ \in [0,n]) \end{align} 使用點乘計算相似度:sij?=Qi??Kj????(i,j?∈[0,n])??
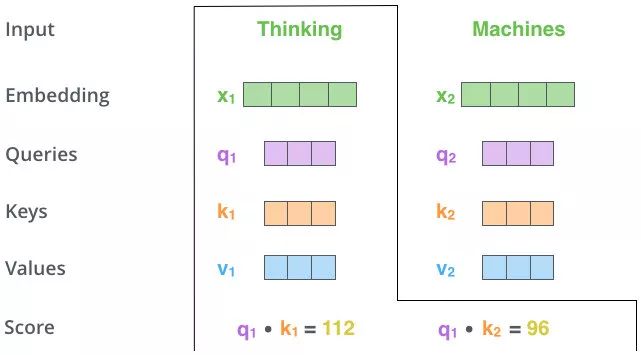
-
歸一化+softMax
需要對前面得到的sij進行歸一化:除以縮放因子dKdK:K的維度sij′=sijdKAi=softMax(S′)=exp(sij′)∑k=1nexp(sik′) \begin{align} 需要對前面得到的s_{ij}進行歸一化:除以縮放因子\sqrt{d_K}\\ d_K:K的維度\\ s_{ij}' = \frac{s_{ij}}{\sqrt{d_{K}}}\\ A_i = softMax(S') = \frac{exp(s'_{ij})}{\sum_{k=1}^{n}exp(s'_{ik})} \end{align} 需要對前面得到的sij?進行歸一化:除以縮放因子dK??dK?:K的維度sij′?=dK??sij??Ai?=softMax(S′)=∑k=1n?exp(sik′?)exp(sij′?)???
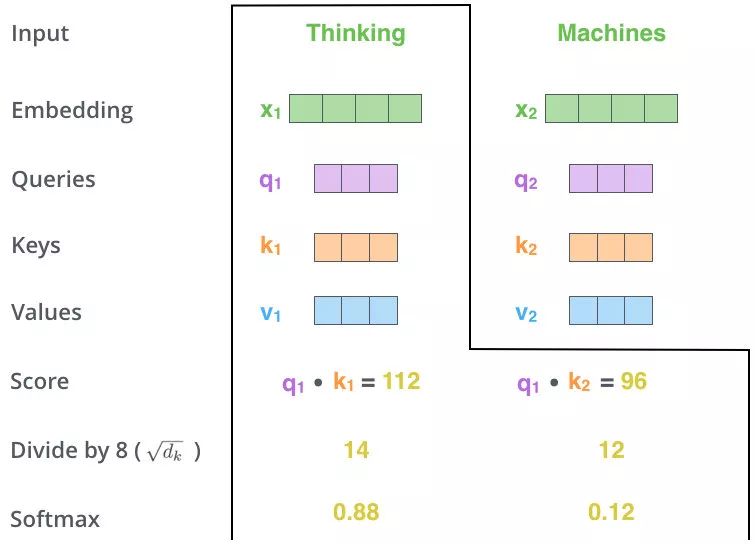
- 加權求和
Zi=Ai?Vi \begin{align} Z_i = A_i \cdot V_i\\ \end{align} Zi?=Ai??Vi???
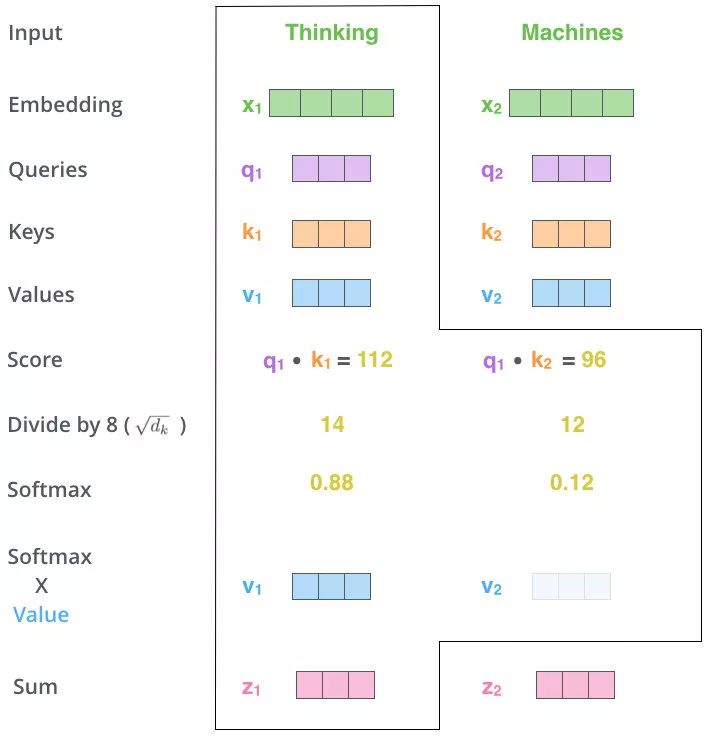
以矩陣形式:
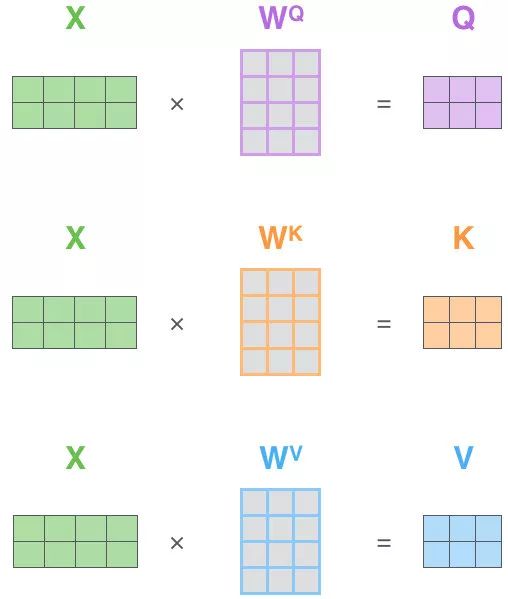
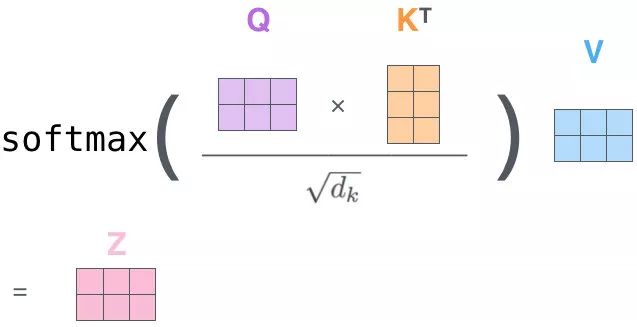
對于這個softMax:
Qi?KiT是一個word2word的attention?Map經過softMax后:矩陣內每個元素和為1,相當于每個元素之間都有對應的權重
\begin{align}
Q_i\cdot K_i^T是一個word2word的attention\ Map \\
經過softMax后:\\
矩陣內每個元素和為1,相當于每個元素之間都有對應的權重
\end{align}
Qi??KiT?是一個word2word的attention?Map經過softMax后:矩陣內每個元素和為1,相當于每個元素之間都有對應的權重??
假設輸入"I have a dream":

形成了一張4×4的注意力圖,每個單詞與單詞之間都有對應的權重
與普通Attention機制的區別
- 普通Attention:
- 在Encoder-Decoder模型中,查詢向量Q是Decoder的輸出,K和V位于Encoder
- self Attention:
- 在Encoder-Decoder模型中,Q,K,V都是Encoder中的元素
與RNNs相比
- self Attention 將任意兩個單詞通過一個計算步驟Qi?KjQ_i\cdot K_jQi??Kj?動態聯系在一起,不會存在RNNs中有效信息隨時間序列推移而變得難以捕獲的問題
- 并且RNNs計算是通過時間步序列進行串行,而self Attention可以對一句話中的每個單詞單獨的進行 Attention 值的計算,也就是說可以并行計算
Masked Self Attention掩碼自注意力機制
架構
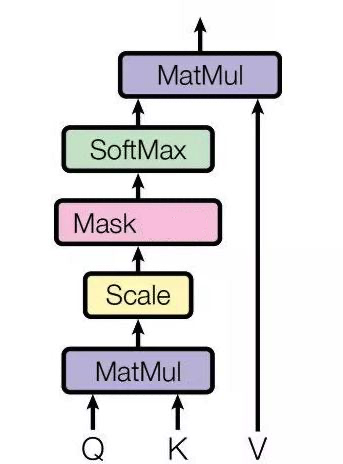
相較于self Attention:在歸一化和softMax之間多了一層Masked操作
Masked指的是:在做語言模型(如機器翻譯,文本生成…)時,不給模型看到未來的信息
假設在Masked之前,我們已經得到了一個attentionMap:

Masked要做的就是,只保留下三角矩陣
如這個形式:
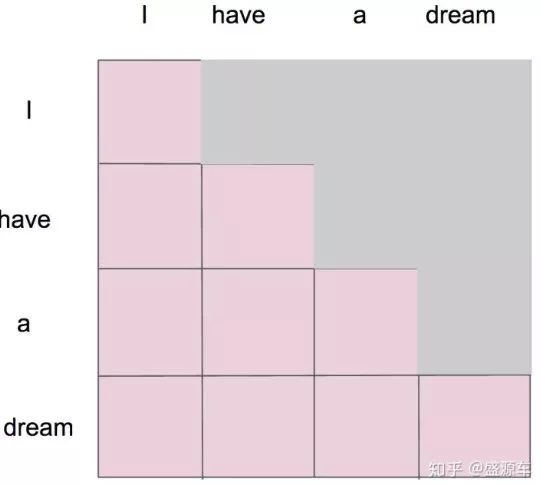
如何理解(?)
- 對于單一個單詞"I"
- 只能和
"I"自己有attention
- 只能和
- 對于第二個單詞"have"
- 只能和
"I","have"有attention
- 只能和
- 對于第三個單詞"a"
- 只能和
"I","have","a"有attention
- 只能和
- 對于第四個單詞"dream"
- 只能和
"I","have","a","dream"有attention
- 只能和
Masked后的attentionMap矩陣,經softMax處理后,橫軸的attention weight之和為1
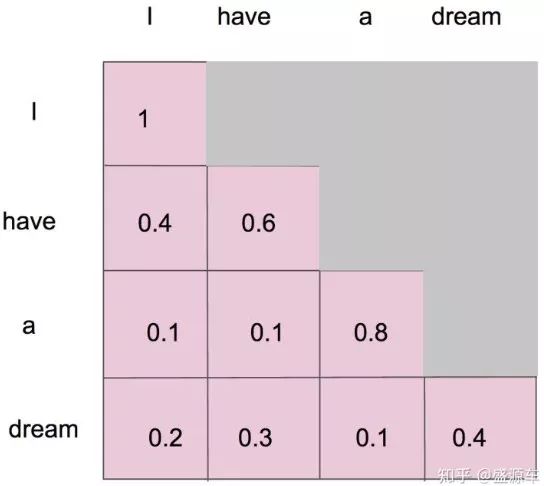
Attention(Q,K,V)計算公式變為:
Attention(Q,K,V)=Zi=softMax(sijdK+Mask)?V Attention(Q,K,V) = Z_i = softMax(\frac{s_{ij}}{\sqrt{d_K}}+Mask)\cdot V Attention(Q,K,V)=Zi?=softMax(dK??sij??+Mask)?V
Multi-head Self Attention多頭自注意力機制
回顧一下self Attention的整個流程:
對于序列X中第i個單詞Xi的詞向量xi??(i?∈(0,n]):Qi=xi?WQ,Ki=xi?WK,Vi=xi?WV使用點乘計算相似度:sij=Qi?Kj???(i,j?∈[0,n])sij′=sijdKAi=softMax(S′)=exp(sij′)∑k=1nexp(sik′)Zi=Ai?Vi
\begin{align}
對于序列X中第i個單詞X_i的詞向量x_i\ \ (i \ \in (0,n]):\\
Q_i = x_i \cdot W_Q,
K_i = x_i \cdot W_K,
V_i = x_i \cdot W_V \\
使用點乘計算相似度:\\
s_{ij} = Q_i \cdot K_j\ \ \ (i,j\ \in [0,n]) \\
s_{ij}' = \frac{s_{ij}}{\sqrt{d_{K}}}\\
A_i = softMax(S') = \frac{exp(s'_{ij})}{\sum_{k=1}^{n}exp(s'_{ik})}\\
Z_i = A_i \cdot V_i\\
\end{align}
對于序列X中第i個單詞Xi?的詞向量xi???(i?∈(0,n]):Qi?=xi??WQ?,Ki?=xi??WK?,Vi?=xi??WV?使用點乘計算相似度:sij?=Qi??Kj????(i,j?∈[0,n])sij′?=dK??sij??Ai?=softMax(S′)=∑k=1n?exp(sik′?)exp(sij′?)?Zi?=Ai??Vi???
所謂的多頭,就是對于self Attention的加權求和得到的Z分割成n份 Z1,Z2,??,ZnZ_1,Z_2,\cdots,Z_nZ1?,Z2?,?,Zn?
n通常取8
經過全連接層后,獲得一個新的Z′Z'Z′
架構
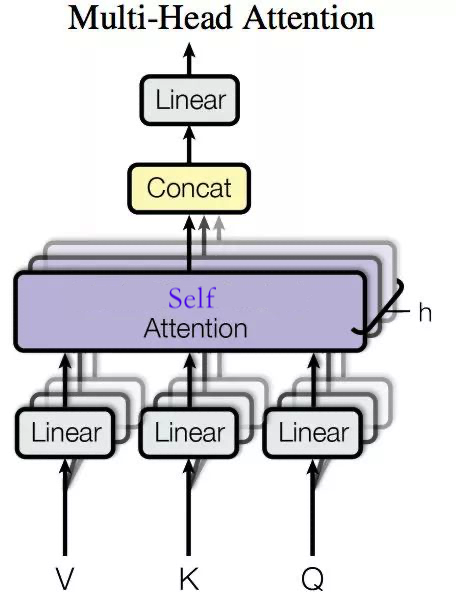
輸入序列x通過與h個不同的WQ,WK,WV進行線性變換,得到h個不同的Q,K,V,最后得到h個Z,拼接后與另一個矩陣W進行線性變化后,得到Z′輸入序列x通過與h個不同的W_Q,W_K,W_V進行線性變換,得到h個不同的Q,K,V,最后得到h個Z,拼接后與另一個矩陣W進行線性變化后,得到Z'輸入序列x通過與h個不同的WQ?,WK?,WV?進行線性變換,得到h個不同的Q,K,V,最后得到h個Z,拼接后與另一個矩陣W進行線性變化后,得到Z′
流程
- 定義多組W,生成多組Q,K,V
Qik=xi?WkQKik=xi?WkKVik=xi?WkVk∈[0,h?1] \begin{align} Q_{ik} = x_i\cdot W_{k}^{Q}\\ K_{ik} = x_i\cdot W_{k}^{K}\\ V_{ik} = x_i\cdot W_{k}^{V}\\ k \in [0,h-1] \end{align} Qik?=xi??WkQ?Kik?=xi??WkK?Vik?=xi??WkV?k∈[0,h?1]?? - 得到多組Attention(Q,K,V)
sik,jk=Qik?KjkAik=softMax(sik,jkdK)Zik=Aik?Vik \begin{align} s_{ik,jk} = Q_{ik}\cdot K_{jk} \\ A_{ik} = softMax(\frac{s_{ik,jk}}{\sqrt{d_{K}}})\\ Z_{ik} = A_{ik}\cdot V_{ik}\\ \end{align} sik,jk?=Qik??Kjk?Aik?=softMax(dK??sik,jk??)Zik?=Aik??Vik??? - 多組輸出拼接后,與W0進行線性變換,降低維度
拼接:Zi=concat([Zi1,Zi2,??,Zih]))Zi′=W0?Zi \begin{align} 拼接:\\ Z_i = concat([Z_{i1},Z_{i2},\cdots,Z_{ih}])) \\ Z_i' = W_0\cdot Z_i \end{align} 拼接:Zi?=concat([Zi1?,Zi2?,?,Zih?]))Zi′?=W0??Zi???
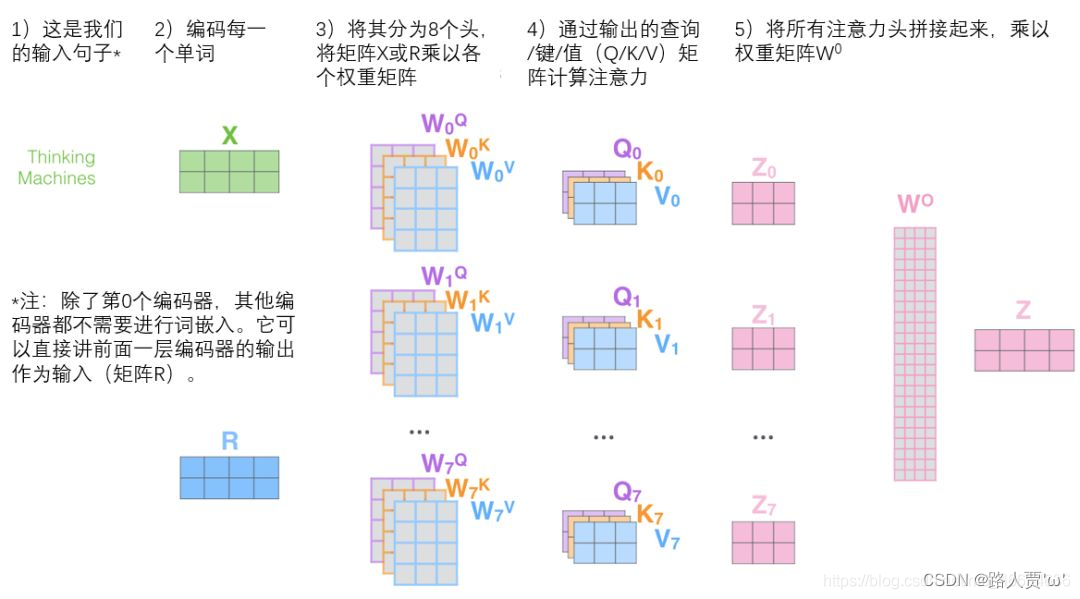
注意:除了第0個Encoder,其他Encoder都不需要進行word Embedding;它可以將前面一層Encoder的輸出作為輸入
為什么(?)
因為還沒學到Transformer,所以暫時回答不上來qaq;
學完Transformer的架構后再解答
)
)


——numpy庫)


)




)


![[Oracle] UNPIVOT 列轉行](http://pic.xiahunao.cn/[Oracle] UNPIVOT 列轉行)



