二叉搜索樹深度解析：從原理實現到算法應用----《Hello C++ Wrold!》(18)--(C/C++)

文章目錄

  • 前言
  • 二叉搜索樹（二叉排序樹或二叉查找樹）
    • 二叉搜索樹的模擬實現
    • 二叉搜索樹和有序數組二分查找的比較
    • 兩個搜索模型
  • 作業部分

前言

二叉搜索樹（Binary Search Tree，簡稱 BST）作為一種重要的樹形數據結構，在計算機科學領域有著廣泛的應用。它憑借其基于鍵值的有序性，能夠高效地支持數據的插入、刪除和查找等操作，是許多復雜算法和系統的基礎組件。

本文將圍繞二叉搜索樹展開全面而深入的探討。首先，我們將從其核心定義和關鍵性質出發，幫助讀者建立對二叉搜索樹的基本認知，包括其通過中序遍歷可得到升序序列這一重要特性。隨后，詳細剖析二叉搜索樹的各項基本操作，如插入、查找、刪除等，并通過 C++ 代碼實現進行具體演示，同時對比遞歸與非遞歸實現方式的異同。

此外，我們還將對二叉搜索樹與有序數組的二分查找進行對比分析，明確各自的優勢與局限。最后，結合一系列經典的算法題目，如二叉搜索樹與雙向鏈表的轉換、根據遍歷序列構造二叉樹、二叉樹的非遞歸遍歷等，展示二叉搜索樹在實際問題中的應用，幫助讀者鞏固所學知識，提升解決復雜問題的能力。無論是數據結構初學者，還是希望深化對二叉搜索樹理解的開發者，都能從本文中獲得有價值的參考。

二叉搜索樹（二叉排序樹或二叉查找樹）

概念:是一顆空樹或者是具有以下性質的二叉樹:

1.若左子樹不為空，則左子樹上所有節點的值都小于根節點的值

2.若右子樹不為空，則右子樹上所有節點的值都大于根節點的值

3.它的左右子樹也分別為二叉搜索樹

引申:a.用中序遍歷去遍歷二叉搜索樹的結果正好是升序

    b.查找其中元素的最壞時間復雜度是O(n)--n表示n個元素

比如:在這里插入圖片描述

c.結點左邊所有的樹都比結點小;結點右邊所有的樹都比結點大

二叉搜索樹的模擬實現

template<class K>
struct BSTreeNode
{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr),_right(nullptr),_key(key){}
};template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
public:BSTree():_root(nullptr){}BSTree(const BSTree<K>& t)
{_root = Copy(t._root);
}BSTree<K>& operator=(BSTree<K> t)
{swap(_root, t._root);//理解!return *this;
}~BSTree()
{Destroy(_root);
}bool Insert(const K& key)//插入不了重復的值{if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (key>cur->_key){parent = cur;cur = cur->_right;}else if(key< cur->_key){parent = cur;cur = cur->_left;//cur只是里面存的值變成了他的}else{return false;}}cur = new Node(key);//把開辟好的地址存在了cur里面if (key > parent->_key){parent->_right = cur;//本來里面是nullptr;}else{parent->_left = cur;}return true;}bool Find(const K& key){Node* cur = _root;while (cur){if (key > cur->_key){cur = cur->_right;}else if (key < cur->_key){cur = cur->_left;}else{return true;}}return false;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (key > cur->_key){parent = cur;cur = cur->_right;}else if (key < cur->_key){parent = cur;cur = cur->_left;}else // 找到了{// 左為空if (cur->_left == nullptr){if (cur == _root){_root = cur->_right;}else{if (parent->_right == cur){parent->_right = cur->_right;}else{parent->_left = cur->_right;}}}// 右為空else if (cur->_right == nullptr){if (cur == _root){_root = cur->_left;}else{if (parent->_right == cur){parent->_right = cur->_left;}else{parent->_left = cur->_left;}}	} // 左右都不為空 else{// 找替代節點Node* parent = cur;//這里不能是nullptr,不然要刪的地方是根節點就慘了Node* leftMax = cur->_left;while (leftMax->_right){parent = leftMax;leftMax = leftMax->_right;}swap(cur->_key, leftMax->_key);if (parent->_left == leftMax){parent->_left = leftMax->_left;}else{parent->_right = leftMax->_left;
//這個就是左子樹存在右子樹的情況}//這里要注意!!!cur = leftMax;}delete cur;return true;}}return false;}void InOrder(){_InOrder(_root);cout << endl;}/*bool FindR(const K& key)
{return _FindR(_root, key);
}bool InsertR(const K& key)
{return _InsertR(_root, key);
}bool EraseR(const K& key)
{return _EraseR(_root, key);
}*/用遞歸實現這些函數private:/*bool _EraseR(Node*& root, const K& key)這種樹形遞歸的話一般都要傳這個root{if (root == nullptr)return false;if (root->_key < key){return _EraseR(root->_right, key);}else if (root->_key > key){return _EraseR(root->_left, key);}else{Node* del = root;// 1、左為空// 2、右為空// 3、左右都不為空if (root->_left == nullptr){root = root->_right;}else if (root->_right == nullptr){root = root->_left;}else{Node* leftMax = root->_left;這里可不是傳的引用while (leftMax->_right){leftMax = leftMax->_right;}swap(root->_key, leftMax->_key);return _EraseR(root->_left, key);這里不能是(leftMax,key)!!!倒不是它是局部變量的關系}delete del;return true;}}bool _InsertR(Node*& root, const K& key)這里用&就非常好{if (root == nullptr){root = new Node(key);return true;}if (root->_key < key){return _InsertR(root->_right, key);}else if (root->_key > key){return _InsertR(root->_left, key);}else{return false;}}bool _FindR(Node* root, const K& key){if (root == nullptr)return false;if (root->_key < key){return _FindR(root->_right, key);}else if (root->_key > key){return _FindR(root->_left, key);}else{return true;}}*/這是用遞歸實現的函數void _InOrder(Node* root){if (root == NULL){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* copyroot = new Node(root->_key);copyroot->_left = Copy(root->_left);copyroot->_right = Copy(root->_right);return copyroot;}//這里用的是前序遍歷,用中序可不行void Destroy(Node*& root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;}
private:Node* _root;
};

引申:1.swap對于基本類型，交換的是值;對于指針，交換的是指針里面存的值

    2.二叉搜索樹的刪除操作的模擬實現做法:

找到后分情況:
1.結點沒有孩子--直接刪
2.結點有一個孩子--托孤
3.結點有兩個孩子--替換法:該結點跟左子樹的最右(最大)結點或右子樹的最左(最小)結點替換,然后刪除

3.關于引用,平時說的話就是不開空間,探討底層匯編才考慮它其實是占了空間的

二叉搜索樹和有序數組二分查找的比較

二分查找的話，插入和刪除的效率不太行

二叉搜索樹的話，查找排序插入刪除效率都不錯，但是下限太低了,如圖:

在這里插入圖片描述

兩個搜索模型

1.key的搜索模型:快速判斷在不在

eg:門禁系統 小區車輛出入系統

比如:檢查一篇英文文章，看單詞是否拼寫正確
做法:讀取詞庫到一顆搜索樹上，讀取單詞，看在不在-不在就是拼寫錯誤

2.key/value的搜索模型:通過一個值找另外一個值

eg:商場的車輛出入系統 高鐵實名制車票系統

舉例:統計水果出現的次數
做法:第一次出現的話，要插入這個水果名和它出現的次數為1不是第一次的話，直接次數++就行了

注意:key一般是不允許重復的信息!

k-v模型的話，在上面的二叉搜索樹的模擬實現里面,成員變量要加個value,Insert和erase操作的形參要加value

作業部分

下面關于二叉搜索樹正確的說法是（C）
A.待刪除節點有左子樹和右子樹時，只能使用左子樹的最大值節點替換待刪除節點
B.給定一棵二叉搜索樹的前序和中序遍率歷結果，無法確定這棵二叉搜索樹
C.給定一棵二叉搜索樹，根據節點值大小排序所需時間復雜度是線性的
D.給定一棵二叉搜索樹，可以在線性時間復雜度內轉化為平衡二叉搜索樹引申:使用兩個遍歷結果確定樹的結構， 其中有一個遍歷結果必須要是中序遍歷結果,這樣就可以

牛客網 JZ36 二叉搜索樹與雙向鏈表

牛客網    JZ36 二叉搜索樹與雙向鏈表
做法:也就是把當前在的地方的left改成指向中序遍歷上一個結點，把right改成指向中序遍歷下一個結點在前序遍歷改結點的時候:prev一定要傳引用
注意:最后返回的結點多半不是開頭給的那個結點易忘這一步:if(prev) prev->right = cur;

代碼展示:
/*
struct TreeNode {int val;struct TreeNode *left;struct TreeNode *right;TreeNode(int x) :val(x), left(NULL), right(NULL) {}
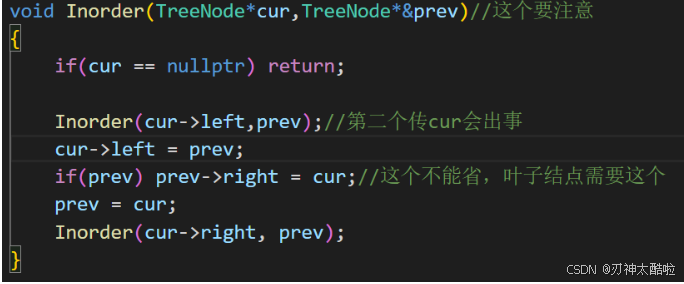
};*/void Inorder(TreeNode*cur,TreeNode*&prev)//這個要注意
{if(cur == nullptr) return;Inorder(cur->left,prev);//第二個傳cur會出事cur->left = prev;if(prev) prev->right = cur;//這個不能省，葉子結點需要這個prev = cur;Inorder(cur->right, prev);
}class Solution {
public:TreeNode* Convert(TreeNode* pRootOfTree) {TreeNode* prev = nullptr;Inorder(pRootOfTree, prev);while(pRootOfTree&&pRootOfTree->left) pRootOfTree = pRootOfTree->left;return pRootOfTree;}
};

在這里插入圖片描述

引申:while和if自己老是容易寫混

力扣 606. 根據二叉樹創建字符串

力扣 606. 根據二叉樹創建字符串
這道題最主要是()的處理:
1.左邊為空，右邊不為空->左邊右邊括號都保留
2.左邊不為空，右邊為空->左邊括號保留
3.左邊右邊都為空->左邊右邊的括號都不保留注意:root->val記得轉化成string類型的

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:string tree2str(TreeNode* root) {string s1;if(root == nullptr) return "";else s1+=to_string(root->val);if(root->left||root->right){s1+="(";s1+= tree2str(root->left); s1+=")";}if(root->right)//{s1+="(";s1+=tree2str(root->right); s1+=")";}return s1;}
};

在這里插入圖片描述

注意理解這里局部變量s1的用法

力扣 236. 二叉樹的最近公共祖先

力扣   236. 二叉樹的最近公共祖先
做法1:時間復雜度為O(N平方)
先查找,看p,q看該結點的左邊還是右邊->一個在左一個在右這個結點就是最近公共祖先在同一邊就要遞歸去那一邊再來
注意:p,q其中一個可能就是最近公共祖先做法2:時間復雜度為O(n)
搞了兩個棧,把到p,q的路徑存在了棧里面，之后根據他們的公共祖先高度應該一樣來找

代碼展示:
/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:bool Find(TreeNode*root,TreeNode*target,stack<TreeNode*>&path)//{if(root == nullptr) return false;path.push(root);if(root == target) return true;if(Find(root->left,target,path)) return true;if(Find(root->right,target,path)) return true;path.pop();return false;}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {stack<TreeNode*> p1,q1;Find(root,p,p1);Find(root,q,q1);while(p1.size()>q1.size())   p1.pop();while(p1.size()<q1.size())   q1.pop();while(p1.top()!=q1.top()){p1.pop(); q1.pop();}return p1.top();}
};

在這里插入圖片描述

上面是做法2的Find的寫法

力扣 105. 從前序與中序遍歷序列構造二叉樹

力扣    105. 從前序與中序遍歷序列構造二叉樹
做法: 用前序去確定根的位置，用中序去分割左右區間（也就是中序去判斷完沒完）
注意:root創建空間的寫法: TreeNode*root = new TreeNode(preorder[previ]);previ要帶引用,傳參時不能傳個0過去這樣!

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* _build(vector<int>& preorder, vector<int>& inorder,int&previ,int begini,int endi) {if(begini>endi) return nullptr;TreeNode*root = new TreeNode(preorder[previ]);int rooti = begini;while(rooti<=endi){if(preorder[previ] == inorder[rooti])   break;rooti++;}++previ;root->left = _build(preorder,inorder,previ,begini,rooti-1);root->right = _build(preorder,inorder,previ,rooti+1,endi);return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int n = (int)preorder.size()-1; int p = 0;return _build(preorder,inorder,p,0,n);}
};

自己實現的函數:在這里插入圖片描述

力扣 106. 從中序與后序遍歷序列構造二叉樹
力扣 144. 二叉樹的前序遍歷(自己要求自己用非遞歸的形式完成)
力扣 94. 二叉樹的中序遍歷(自己要求自己用非遞歸的形式完成)
力扣 145. 二叉樹的后序遍歷(自己要求自己用非遞歸的形式完成)

力扣 106. 從中序與后序遍歷序列構造二叉樹
跟上面做法的區別:previ要從最后開始取,然后根構建完之后先構建右樹代碼展示:
/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:
TreeNode* _build(vector<int>& postorder, vector<int>& inorder,int&previ,int begini,int endi) {if(begini>endi) return nullptr;//TreeNode*root = new TreeNode(postorder[previ]);int rooti = begini;while(rooti<=endi){if(postorder[previ] == inorder[rooti])   break;rooti++;}--previ;root->right = _build(postorder,inorder,previ,rooti+1,endi);root->left = _build(postorder,inorder,previ,begini,rooti-1);return root;}TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {int p = postorder.size()-1;return _build(postorder,inorder,p,0,postorder.size()-1);}
};

力扣 144. 二叉樹的前序遍歷(自己要求自己用非遞歸的形式完成)
做法:訪問左路結點(此時就把結點的值搞到vector里面),左路結點全入棧，后續依次訪問左路結點的右子樹力扣   94. 二叉樹的中序遍歷(自己要求自己用非遞歸的形式完成)
做法:改成在出棧的時候再把結點存vector里就行了

代碼展示:
中序遍歷:
/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int>v;  stack<TreeNode*> st;TreeNode* cur = root;while(cur||!st.empty()){while(cur){st.push(cur);cur = cur->left;}TreeNode*top = st.top();st.pop();   v.push_back(top->val);cur = top->right;}return v;}
};前序遍歷:
/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {vector<int>v;  stack<TreeNode*> st;TreeNode* cur = root;while(cur||!st.empty()){while(cur){v.push_back(cur->val);st.push(cur);cur = cur->left;}TreeNode*top = st.top();st.pop();cur = top->right;}return v;}
};

力扣  145. 二叉樹的后序遍歷(自己要求自己用非遞歸的形式完成)
做法:加一個prev來記錄上一個存了的結點是啥改成在一個結點的右子樹為空或者上一個訪問結點是右子樹的根時再訪問這個結點下面是與前面兩道題相差比較大的地方

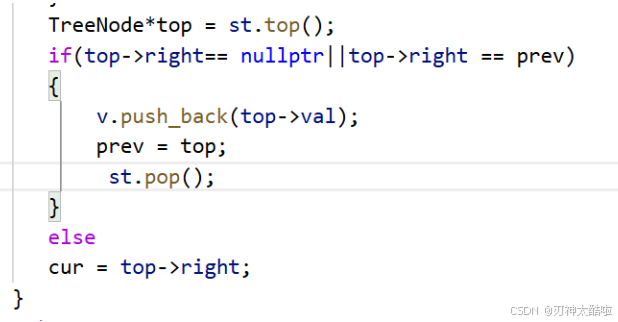
在這里插入圖片描述

代碼展示:
/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {vector<int>v;  stack<TreeNode*> st;TreeNode* cur = root; TreeNode*prev = nullptr;while(cur||!st.empty()){while(cur){st.push(cur);cur = cur->left;}TreeNode*top = st.top();     if(top->right== nullptr||top->right == prev){v.push_back(top->val);prev = top;st.pop();}elsecur = top->right;}return v;}
};

二叉樹的后序非遞歸遍歷中，需要的額外空間包括（C）
A.一個棧
B.一個隊列
C.一個棧和一個記錄標記的順序表
D.一個隊列和一個記錄標記的順序表
注意:vector別忘了他是順序表!

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/diannao/95132.shtml
繁體地址，請注明出處：http://hk.pswp.cn/diannao/95132.shtml
英文地址，請注明出處：http://en.pswp.cn/diannao/95132.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

牛客.空調遙控二分查找牛客.kotori和氣球（數學問題)力扣.二叉樹的最大路徑和牛客.主持人調度(二)

牛客.空調遙控二分查找牛客.kotori和氣球（數學問題)力扣.二叉樹的最大路徑和牛客.主持人調度(二)

目錄 牛客.空調遙控 二分查找 牛客.kotori和氣球&#xff08;數學問題) 力扣.二叉樹的最大路徑和 牛客.主持人調度(二) 牛客.空調遙控 枚舉n個空調之后&#xff0c;使數組有序&#xff0c;左右下標&#xff0c;用二分查找&#xff0c;然后一個求 長度就好 二分查找 /二分理…
閱讀更多...
《嵌入式Linux應用編程（二）：標準IO高級操作與文件流定位實戰》

《嵌入式Linux應用編程（二）：標準IO高級操作與文件流定位實戰》

今日學習內容1. 行輸入函數安全實踐(1) fgets vs gets函數安全特性換行符處理緩沖區保護fgets指定讀取長度&#xff08;size-1&#xff09;保留\n并添加\0安全&#xff08;防溢出&#xff09;gets無長度限制將\n替換為\0危險2. Linux標準文件流文件流符號設備 標準輸入stdin鍵盤…
閱讀更多...
Springboot2+vue2+uniapp 小程序端實現搜索聯想自動補全功能

Springboot2+vue2+uniapp 小程序端實現搜索聯想自動補全功能

目錄 一、實現目標 1.1 需求 1.2 實現示例圖: 二、實現步驟 2.1 實現方法簡述 2.2 簡單科普 2.3 實現步驟及代碼 一、實現目標 1.1 需求 搜索聯想——自動補全 &#xff08;1&#xff09;實現搜索輸入框&#xff0c;用戶輸入時能顯示模糊匹配結果 &am…
閱讀更多...
極簡 5 步：Ubuntu+RTX4090 源碼編譯 vLLM

極簡 5 步：Ubuntu+RTX4090 源碼編譯 vLLM

極簡 5 步&#xff1a;UbuntuRTX4090 源碼編譯 vLLM1. 系統依賴&#xff08;一次性&#xff09;2. 進入源碼目錄 & 激活環境3. 啟用 ccache 自動并行度4. 拉代碼 編譯&#xff08;2 行搞定&#xff09;5. 更新 flash-attn&#xff08;與 vLLM 配套&#xff09;6. 啟動 4 …
閱讀更多...
生產工具革命：定制開發開源AI智能名片S2B2C商城小程序重構商業生態的范式研究

生產工具革命：定制開發開源AI智能名片S2B2C商城小程序重構商業生態的范式研究

摘要互聯網作為信息工具已深刻改變商業生態&#xff0c;但其本質仍停留在效率優化層面。本文提出&#xff0c;基于定制開發開源AI智能名片與S2B2C商城小程序的深度融合&#xff0c;正在引發生產工具層面的革命性變革。該技術架構通過重構"人-貨-場"關系&#xff0c;實…
閱讀更多...
Transformer前傳:Seq2Seq與注意力機制Attention

Transformer前傳:Seq2Seq與注意力機制Attention

前言 參考了以下大佬的博客 https://blog.csdn.net/v_july_v/article/details/127411638 https://blog.csdn.net/andy_shenzl/article/details/140146699 https://blog.csdn.net/weixin_42475060/article/details/121101749 https://blog.csdn.net/weixin_43334693/article/det…
閱讀更多...
企業架構工具篇之ArchiMate的HelloWorld(2)

企業架構工具篇之ArchiMate的HelloWorld(2)

本文通過ArchiMate做一個員工報銷流程設計的小demo，按照步驟都可以做出來，在做這個demo之前先簡單認識下Archimate的開發界面： 模型樹（Models）窗口：通常位于左上方，以樹形結構展示一個或多個 ArchiMate 模型。用戶可在此瀏覽模型的整體結構，快速定位到特定的模型元素，…
閱讀更多...
Docker 詳解(保姆級安裝+配置+使用教程)

Docker 詳解(保姆級安裝+配置+使用教程)

文章目錄一、初識 Docker二、Docker 命令1、安裝2、配置鏡像加速器檢查配置是否生效3、服務相關命令4、鏡像相關命令5、容器相關命令三、Docker 容器數據卷1、數據卷概念2、數據卷作用3、配置數據卷4、配置數據卷容器四、Docker 應用部署五、備份與遷移六、Dockerfile七、Docke…
閱讀更多...
做調度作業提交過程簡單介紹一下

做調度作業提交過程簡單介紹一下

?作業提交與執行流程前文提到在 Linux 的 HPC 或超算環境中&#xff0c;可以只在共享存儲上安裝一次應用程序&#xff0c;然后所有計算節點通過掛載共享目錄來訪問和執行這些程序&#xff0c;那么作業提交及執行過程是怎么樣的流程呢&#xff1f;結構說明&#xff1a;第一行是…
閱讀更多...
【Altium designer】解決報錯“Access violation at address...“

【Altium designer】解決報錯“Access violation at address...“

問題現象如上AD9原理圖工程所示報錯&#xff0c;當我關閉這個“CMM-WEIER-VA”原理圖工程以及其他不相關的原理圖工程出現報錯&#xff1a;Access violation at address 0832A5EC in module WorkspaceManager.DLL. Read of address 00000061 at 0832A5EC&#xff0c;任務管理器…
閱讀更多...
小杰python高級（three day）——numpy庫

小杰python高級（three day）——numpy庫

1.numpy數組的操作&#xff08;1&#xff09;數組的連接stack該函數可以實現多個數組的堆疊(連接)&#xff0c;會創建新的軸&#xff0c;用于沿著新的軸連接一系列數組&#xff0c;所有數組必須具有相同的形狀。可以增加數組的維度。假設輸入的每個數組都是 n 維數組&#xff0…
閱讀更多...
視頻剪輯的工作流程

視頻剪輯的工作流程

準備素材 1.準備音頻&#xff0c;視頻、圖片等素材 2.準備Pr創建的序列、彩條、字母、倒計時片頭等功能性素材 創建項目 創建項目是詩篇剪輯的第一步&#xff0c;創建一個指定名稱與存放位置的項目文件&#xff0c;用來通義管理整個視頻項目創建序列 序列決定剪輯的尺寸、幀速率…
閱讀更多...
下一個排列 的 思路總結

下一個排列 的 思路總結

文章目錄思路分析&#xff1a; 倒序遍歷&#xff1a;題目要求的是下一個排列&#xff0c;那么肯定數字的跳躍不能太大&#xff0c;所以可以比較好確定的是&#xff0c;遍歷的順序是倒序遍歷比較方向&#xff1a;對于每一個數字&#xff0c;需要找到右邊最大的比它小的數字&…
閱讀更多...
Spring Cloud-面試題(49)

Spring Cloud-面試題(49)

摘要&#xff1a; 1、通俗易懂&#xff0c;適合小白 2、僅做面試復習用&#xff0c;部分來源網絡&#xff0c;博文免費&#xff0c;知識無價&#xff0c;侵權請聯系&#xff01; 1. 什么是Spring Cloud框架&#xff1f;子項目哪幾大類&#xff1f; Spring Cloud是一套分布式系…
閱讀更多...
資源查看-iostat命令

資源查看-iostat命令

文章目錄 系統中未安裝 iostat 命令 1. 監控CPU與磁盤的基礎負載 2. 診斷I/O性能瓶頸 3. 實時監控與動態采樣 4. 特定設備或分區的精細化監控 5. 性能測試與基準數據生成 6. 結合其他工具進行綜合調優 總結 結果輸出速查表 第一部分：CPU統計信息 第二部分：設備/磁盤統計信息（…
閱讀更多...
STM32 HAL庫外設編程學習筆記

STM32 HAL庫外設編程學習筆記

STM32 HAL庫外設編程 1. 概述 本文檔是基于STM32 HAL庫的外設編程學習筆記&#xff0c;主要包括以下外設的配置和使用方法&#xff1a; GPIO&#xff1a;通用輸入輸出接口ADC&#xff1a;模數轉換器UART&#xff1a;通用異步收發器TIM&#xff1a;定時器I2C&#xff1a;內部…
閱讀更多...
DHCP服務配置與管理實戰指南

DHCP服務配置與管理實戰指南

DHCP 服務配置與管理筆記 一、DHCP 核心概念 1. DHCP 定義與功能 DHCP (Dynamic Host Configuration Protocol)&#xff1a;動態主機配置協議核心功能&#xff1a; 自動分配 IP 地址提供子網掩碼、網關、DNS 等網絡參數管理 IP 地址租約周期 典型應用&#xff1a;ADSL撥號、企業…
閱讀更多...
WebSocket 在多線程環境下處理 Session并發

WebSocket 在多線程環境下處理 Session并發

WebSocket 在多線程環境下處理 Session并發時&#xff0c;常見問題包括狀態沖突&#xff08;如 IllegalStateException&#xff09;、消息亂序、連接超時等。以下是綜合各技術方案的解決方案&#xff0c;分為單機多線程和分布式集群兩類場景&#xff1a;&#x1f512; 一、單機…
閱讀更多...
JDBC的連接過程(超詳細）

JDBC的連接過程(超詳細）

JDBC&#xff08;Java Database Connectivity&#xff09;是 Java 用于訪問數據庫的標準 API&#xff0c;它允許 Java 程序與各種不同類型的數據庫進行交互&#xff0c; 其連接數據庫的過程主要包含以下幾個步驟&#xff1a;1. 導入 JDBC 驅動依賴在使用 JDBC 連接數據庫之前&a…
閱讀更多...
本地WSL部署接入 whisper + ollama qwen3:14b 總結字幕校對增強版

本地WSL部署接入 whisper + ollama qwen3:14b 總結字幕校對增強版

1. 實現功能 M4-4: 校對增強版 (最終完全體) 本腳本是整個 Module 的最終形態&#xff0c;采用了“代碼預處理 LLM校對”的終極方案&#xff1a; 代碼預處理: 確定性地在每個語音片段后添加逗號&#xff0c;生成一份“標點草稿”。LLM校對: LLM 的任務被簡化為“校對和修正”這…
閱讀更多...
最新文章

Copyright @ 2022~2023