問題描述：

兩個相同的硬幣，半徑都是 $r$。一個硬幣（稱為“動硬幣”）沿著另一個固定不動的硬幣（“靜硬幣”）的外邊緣無滑動地滾動一圈，回到起始位置。問：動硬幣自身旋轉了幾圈？

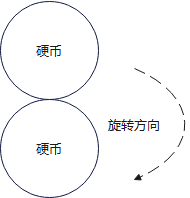
答案是：2圈

這有點奇怪，因為一個硬幣的周長是 $2\pi r$，另一個硬幣的周長也是 $2\pi r$，動硬幣繞著你靜硬幣走一圈，靜硬幣展開成一條直線距離也就 $2\pi r$，怎么就要轉兩圈呢？

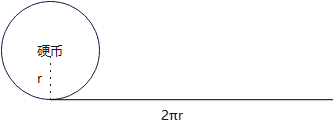
這答案看起來違反直覺，所以叫悖論

誤區澄清

直觀上看，靜硬幣展開成一條直線距離也就 $2\pi r$，所以動硬幣應該只轉一圈

這個想法基于一個假設：動硬幣是沿著一個長度為 $2\pi r$ 的直線滾動。但實際上靜硬幣不能就這么直接展開成一條線，它倆不等價

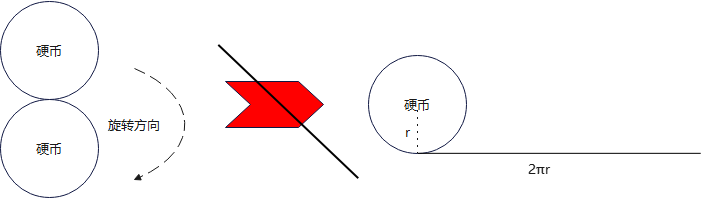
下面來詳細解釋下

直觀解釋

首先，如果動硬幣沿著一條直線滾動，那距離確實就等于靜硬幣的周長

但現在它是沿著一個圓形路徑滾動，路徑的半徑是兩個硬幣半徑之和

$$r+r=2r$$

所以動硬幣的中心走過的路徑是一個半徑為 $2r$ 的圓，周長為

$$C_{path}=2\pi \times (2r)=4\pi r$$

動硬幣的周長是 $2\pi r$，所以它需要自轉

$$\frac{4\pi r}{2\pi r}=2圈$$

所以如果把動硬幣走過的距離看成直線，應該是下圖

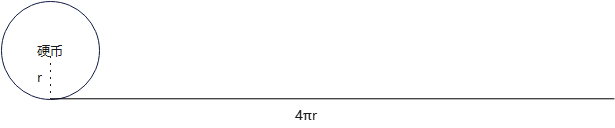
為什么直覺會錯

被接觸點迷惑了！

• 我們以為動硬幣是沿著靜硬幣的周長滾動，所以距離是 $2\pi r$
• 但實際上，滾動的距離是動硬幣中心移動的路徑長度，而不是接觸點的軌跡長度

就像一輛車輪半徑為 $r$ 的車，車輪轉一圈，車向前移動 $2\pi r$ ，但車輪中心也移動了
$2\pi r$ 。同理，這里車（動硬幣）是繞著一個大圓（半徑 $2r$）走，所以中心走了 $4\pi r$，自然要轉兩圈

所以看圓的滾動距離，要看中心點移動的距離，而不是接觸點的軌跡長度

兩種旋轉的來源

動硬幣的自轉兩圈可以分解為兩部分：

• 由于平移產生的旋轉（1圈）：好比動硬幣沿著一條長 $2\pi r$ 的直線滾動，它會轉1圈
• 由于路徑是圓形而產生的額外旋轉，也就是自轉（1圈）：即使動硬幣不滾動，只是平移著繞靜止硬幣轉一圈，它的朝向也會相對于固定空間旋轉一整圈（就像月亮繞地球轉，始終有一面向著地球，但在空間中它其實自轉了一圈）

當 平移 + 自轉 同時發生時，這兩個旋轉疊加，總共就是 2 圈

拓展

當動硬幣半徑為 $r$， 而靜止硬幣的半徑是 $3r$ 時，動硬幣繞著靜止硬幣的外邊緣無滑動地滾動一圈，回到起始位置。問：動硬幣自身旋轉了幾圈？

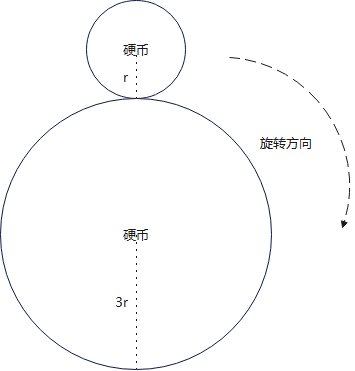
答案是：4圈

同樣，動硬幣繞靜止硬幣中心走一圈的距離取決于它自身的中心軌跡，既然動硬幣緊貼靜止硬幣外側滾動，它的中心實際上是在距離靜止硬幣中心
$$r+3r=4r$$
的位置移動。因此，動硬幣的中心將沿著一個半徑為 $4r$ 的圓周運動

這個圓周的長度（即動硬幣中心走過的路徑長度）可以通過下面的公式計算：
$$C=2\pi \times (半徑)=2\pi \times (4r)=8\pi r$$
所以，動硬幣走過的路徑長度是 $8\pi r$。這意味著，相對于地面，動硬幣會自轉四圈：
$$\frac{8\pi r}{2\pi r}=4$$

同樣，從旋轉來源的視角：

• 由于平移產生的旋轉：好比動硬幣沿著一條長 $6\pi r$ 的直線滾動，它會轉 3 圈
• 由于路徑是圓形而產生的額外旋轉，也就是自轉（1圈）

平移 + 自轉 同時發生，這兩個旋轉疊加，總共就是 4 圈