目錄

一、寫在前面的話

二、KNN（K-Nearest Neighbor）

2.1 KNN算法介紹

2.1.1 概念介紹

2.1.2 算法特點

2.1.3 API 講解

2.2 樣本距離計算

2.2.1 距離的類型

（1）歐幾里得距離（Euclidean Distance）

（2）曼哈頓距離（Manhattan Distance）

（3）切比雪夫距離（Chebyshev Distance）

（4）余弦相似度（Cosine Similarity）

（5）漢明距離（Hamming Distance）

2.2.2 舉例講解計算過程

（1）計算歐幾里得距離

（2）選取K個鄰居

（3）投票預測

2.3 算法的缺陷

（1）計算復雜度高

（2）內存開銷大

（3）對噪聲敏感

（4）維度災難

（5）選擇K值困難

三、模型的評估

3.1 評估指標

3.1.1 對于分類

（1）準確率（Accuracy）

（2）精確度（Precision）

（3）召回率（Recall）

（4）F1-score

3.1.2?對于回歸

（1）均方誤差（MSE, Mean Squared Error）

（2）均方根誤差（RMSE, Root Mean Squared Error）

（3）平均絕對誤差（MAE, Mean Absolute Error）

3.2 交叉驗證

3.2.1?K折交叉驗證（K-Fold Cross-Validation）

（1）介紹

（2）步驟講解

（3）舉例演示

（4）優缺點

3.2.2?留一交叉驗證（Leave-One-Out Cross-Validation，LOO）

3.2.3 分層K折交叉驗證（Stratified K-Fold Cross-Validation）

3.2.4?隨機交叉驗證（Shuffle Split）

四、模型的優化

4.1 優化方法

（1）超參數調優

（2）集成學習（Ensemble Learning）

（3）偏差-方差權衡（Bias-Variance Tradeoff）

（4）正則化技術

4.2 超參數調優

4.2.1 概念介紹

4.2.2 方法分類

4.2.3?網格搜索法介紹

（1）方法步驟

（2）優缺點分析

（3）代碼案例

---

一、寫在前面的話

????????本篇文章將以scikit-learn學習庫使用KNN算法進行分類的介紹與演示，通過對KNN的學習進而引出關于模型的評估與優化的概念，重點介紹交叉驗證與網格搜索方法。

? ? ? ? 機器學習零基礎的讀者可以先去學習一下上一篇文章“新手入門”：

【機器學習】機器學習新手入門概述-CSDN博客

二、KNN（K-Nearest Neighbor）

2.1 KNN算法介紹

2.1.1 概念介紹

• KNN（K-Nearest Neighbor）（也稱為K-近鄰算法）是一種簡單的監督學習算法，主要用于分類和回歸問題。
• 其基于一個非常直觀的原則：對于一個新的樣本，KNN算法通過找到距離它最近的K個已知樣本，根據這些K個樣本的標簽（在分類問題中是類別，在回歸問題中是數值）來進行預測。

2.1.2 算法特點

• KNN算法沒有真正的訓練過程（距離計算的預處理不算入真正訓練），其只是保存所有訓練樣本及其標簽。

2.1.3 API 講解

class sklearn.neighbors.KNeighborsClassifier(n_neighbors=5, algorithm='auto'）

參數: ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
(1)n_neighbors:?
?? ??? ?int, default=5, 默認情況下用于kneighbors查詢的近鄰數，就是K
(2)algorithm:
?? ?{‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}, default=’auto’。找到近鄰的方式，注意不是計算距離的方式，與機器學習算法沒有什么關系，開發中請使用默認值'auto'

方法:
?(1) fit(x， y)?
? ? ? ? 使用X作為訓練數據和y作為目標數據 ?
?(2) predict(X)?? ?預測提供的數據，得到預測數據 ?

2.2 樣本距離計算

????????KNN算法依賴于距離度量進行相似度判斷。根據選擇的距離計算方式，KNN的預測結果將會有所不同。一般來說，歐幾里得距離常用于連續型數據的分類和回歸問題，而對于文本數據，可能會使用余弦相似度來判斷相似度。

2.2.1 距離的類型

（1）歐幾里得距離（Euclidean Distance）

最常見的距離度量方法，適用于連續型變量

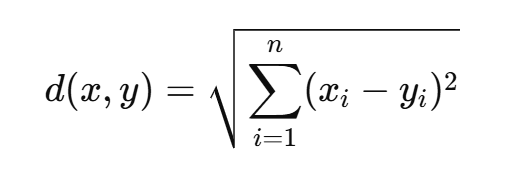
• 其中，x = (x1,x2,…,xn)?和 y = (y1,y2,…,yn) 分別是兩個樣本的特征向量，n是特征的維數。

（2）曼哈頓距離（Manhattan Distance）

曼哈頓距離也叫做城市街區距離，表示兩點在坐標軸上的絕對距離之和。

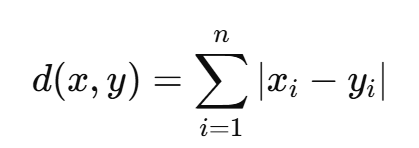
（3）切比雪夫距離（Chebyshev Distance）

切比雪夫距離是兩點在任一坐標軸上的最大距離。

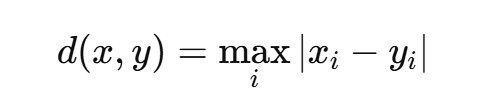
（4）余弦相似度（Cosine Similarity）

用于衡量兩個向量的夾角，適用于文本分類等場景，余弦相似度越大表示兩個樣本越相似。

兩個向量越接近，它們之間的夾角越小，余弦值越接近 1，表示它們的相似度越高。

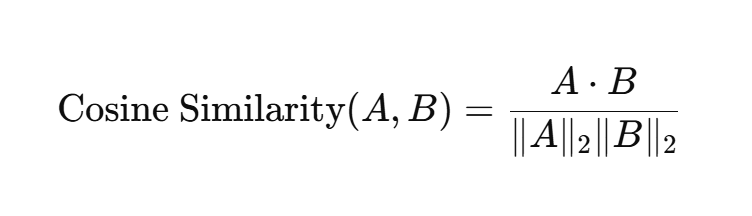
• 其中x * y為兩個向量的點積，∥x∥2?和 ∥y∥2?分別是兩個向量的 L2 范數。
• L1范數：各元素絕對值之和，用于稀疏表示。
• L2范數：各個元素的平方和的平方根，常用于度量向量的“大小”。

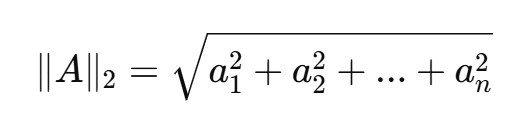
（5）漢明距離（Hamming Distance）

漢明距離用于衡量兩個等長字符串之間的不同位置的個數。

• 例如，對于二進制字符串 x = 10101?和 y = 10011，它們的漢明距離為2。

2.2.2 舉例講解計算過程

假設我們根據X1和X2特征可以預測出標簽Label，即蘋果或是橘子。

現在我們有一個待分類的點?X =（4, 4），要預測它是蘋果還是橘子。

X1	X2	Label
1	1	蘋果
2	1	蘋果
3	2	蘋果
6	5	橘子
7	5	橘子
8	6	橘子

（1）計算歐幾里得距離

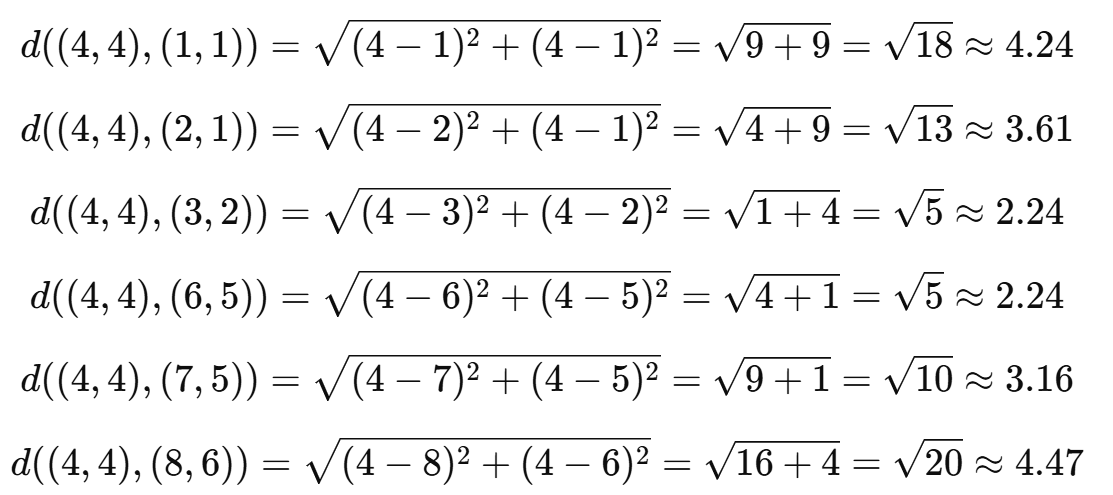
（2）選取K個鄰居

超參數設置，這里我們選擇 K = 3，距離最小的三個點是：(3, 2),? (6, 5),? (7, 5)，它們的標簽分別是：蘋果、橘子、橘子。

（3）投票預測

根據K個最近鄰的標簽（蘋果、橘子、橘子），投票結果是橘子。

2.3 算法的缺陷

（1）計算復雜度高

KNN在測試階段需要計算所有訓練樣本與測試樣本之間的距離，因此當訓練數據集非常大時，KNN的預測速度會非常慢。

（2）內存開銷大

由于KNN需要保存所有訓練數據來進行預測，它的內存消耗也相對較大。

（3）對噪聲敏感

KNN對噪聲數據非常敏感，尤其是在K值較小的時候，噪聲點可能會對最終的分類結果產生很大的影響。

（4）維度災難

當數據集的特征維度過高時，樣本間的距離趨于相似，KNN算法會變得不那么有效。這是因為高維空間的“稀疏性”使得所有樣本的距離差異變得不明顯，導致分類效果下降。

（5）選擇K值困難

選擇合適的K值對于KNN算法的性能至關重要。若K值過小，模型容易過擬合；若K值過大，可能會出現欠擬合。

三、模型的評估

????????模型評估是機器學習過程中的一個重要環節，目的是衡量模型的性能和預測準確性，并通過不同的評估指標來比較和選擇最佳模型。評估的目的是評估模型在未見數據上的表現，確保其不僅僅在訓練集上有良好的效果，而是在實際應用中也能穩定表現。

3.1 評估指標

3.1.1 對于分類

（1）準確率（Accuracy）

最直觀的評估指標，指的是模型正確預測的樣本占總樣本的比例

（2）精確度（Precision）

衡量正類預測準確度，定義為正類預測中實際為正的比例。

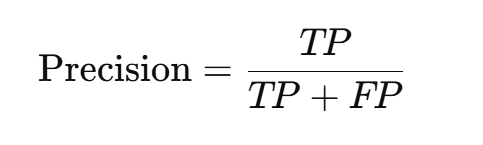
（3）召回率（Recall）

衡量模型識別正類的能力，定義為所有實際為正類樣本中被正確預測為正的比例。

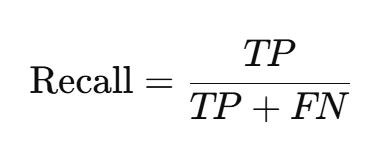
（4）F1-score

精確度和召回率的調和平均值，兼顧了二者的表現，特別適用于類別不平衡的情況。

參數解析：

• TP（True Positives）真陽性：指的是模型正確地將正類樣本預測為正類的數量
• FP（False Positives）假陽性：指的是模型錯誤地將負類樣本預測為正類的數量
• FN（False Negatives）假陰性：指的是模型錯誤地將正類樣本預測為負類的數量?

3.1.2?對于回歸

（1）均方誤差（MSE, Mean Squared Error）

衡量預測值與真實值之間差異的平方平均值，越小表示模型越好。

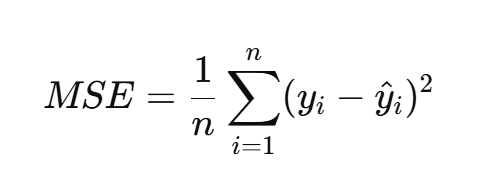
（2）均方根誤差（RMSE, Root Mean Squared Error）

MSE的平方根，具有與原數據相同的單位，便于理解。

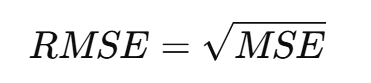
（3）平均絕對誤差（MAE, Mean Absolute Error）

計算預測值與實際值之間的絕對差的平均值，越小越好。

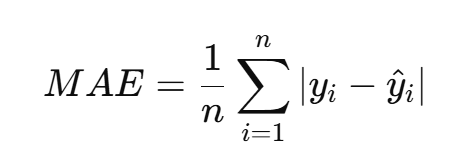
3.2 交叉驗證

交叉驗證（Cross-Validation，簡稱CV），主要目的是為了更穩健地評估模型的性能，避免模型在某一特定訓練集上的過擬合或欠擬合，從而提高模型的泛化能力。現在將其放在評估這里來講解。

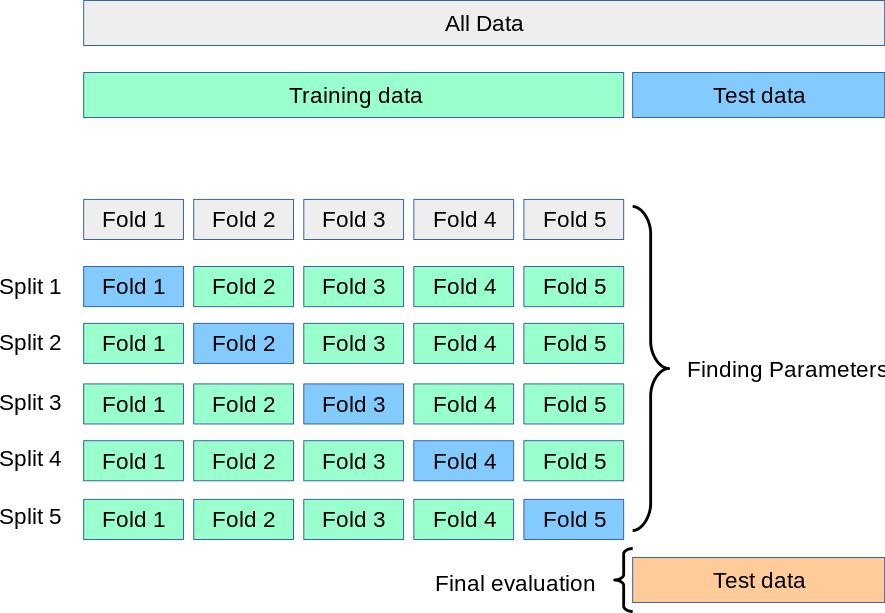
3.2.1?K折交叉驗證（K-Fold Cross-Validation）

（1）介紹

最常用的交叉驗證方法，其基本思想是將數據集分成K個互不重疊的子集（折疊），然后進行K次訓練和驗證。每次訓練時，選擇一個子集作為驗證集，其余K-1個子集作為訓練集。

（2）步驟講解

• 將數據集隨機分成K個大小相同的子集。
• 選擇其中一個子集作為驗證集，剩余的K-1個子集作為訓練集，訓練模型并評估在驗證集上的表現。
• 重復步驟2，直到每個子集都做過一次驗證集。
• 最終的評估結果是所有K次驗證結果的平均值。

（3）舉例演示

假設有一個數據集，隨機劃分成5個子集，用5折交叉驗證來評估一個分類模型的性能：

• 第1輪：用子集1、2、3、4作為訓練集，用子集5作為驗證集，訓練模型并評估其性能。

• 第2輪：用子集1、2、3、5作為訓練集，用子集4作為驗證集，訓練模型并評估其性能。

• 第3輪：用子集1、2、4、5作為訓練集，用子集3作為驗證集，訓練模型并評估其性能。

• 第4輪：用子集1、3、4、5作為訓練集，用子集2作為驗證集，訓練模型并評估其性能。

• 第5輪：用子集2、3、4、5作為訓練集，用子集1作為驗證集，訓練模型并評估其性能。

對于每一輪的評估，我們可以得到一個評估指標（如準確率、精確度、召回率等），最后計算5輪評估結果的平均值，作為模型的最終評估結果。

（4）優缺點

優點：

• 更高的可靠性：相比單一的訓練/測試劃分，K折交叉驗證能更穩定地評估模型性能。
• 每個樣本都有機會成為驗證集：每個數據點都可以參與訓練和測試，提高了評估結果的泛化能力。

缺點：

• 計算開銷大：K折交叉驗證需要進行K次訓練和驗證，如果數據集非常大，計算量和時間開銷也會增加。

3.2.2?留一交叉驗證（Leave-One-Out Cross-Validation，LOO）

（1）介紹

留一交叉驗證是K折交叉驗證的極端情況，其中K等于數據集的大小（即每次訓練時，只用一個樣本作為驗證集，其余的樣本用來訓練模型）。這意味著對于數據集中的每一個樣本，都需要訓練和驗證一次模型。

（2）優缺點

• 優點：每個樣本都能單獨作為驗證集，評估結果非常可靠。

• 缺點：計算成本高：對于非常大的數據集，LOO需要進行大量的訓練和驗證，計算量巨大。

3.2.3 分層K折交叉驗證（Stratified K-Fold Cross-Validation）

（1）介紹

????????在K折交叉驗證中，如果數據集的標簽分布不均衡，某些類別可能在某些折疊中沒有足夠的樣本，導致模型評估不準確。分層K折交叉驗證就是在進行數據集劃分時，保持每個子集中的類別分布盡可能和原始數據集相似。即每個折疊中各類別樣本的比例與整個數據集中的比例一致。

（2）分析

• K-Fold交叉驗證技術中，整個數據集被劃分為K個大小相同的部分。每個分區被稱為 一個”Fold”。所以我們有K個部分，我們稱之為K-Fold。一個Fold被用作驗證集，其余的K-1個Fold被用作訓練集。
• 該技術重復K次，直到每個Fold都被用作驗證集，其余的作為訓練集。
• 模型的最終準確度是通過取k個模型驗證數據的平均準確度來計算的。

3.2.4?隨機交叉驗證（Shuffle Split）

（1）介紹

隨機交叉驗證是一種簡單的交叉驗證方法。它隨機地將數據集分成訓練集和驗證集，并在多次重復中進行評估。每次劃分訓練集和驗證集時，都是隨機的，因此每次劃分的驗證集和訓練集都不同。

（2）優缺點

• 優點：計算量相對較小，且可以任意選擇訓練集和驗證集的比例。

• 缺點：數據劃分可能不穩定，尤其是在類別不平衡時，可能會造成某些類別的數據在驗證集中沒有出現。

四、模型的優化

主要目標是通過調整模型的超參數、改進模型結構或處理數據的方式，來提高模型的預測精度和泛化能力。

4.1 優化方法

這里先簡單列一下優化模型的常見方法：

（1）超參數調優

常見方法：

• 網格搜索（Grid Search）：對所有可能的超參數組合進行窮舉式搜索，找到最優的超參數組合。

• 隨機搜索（Random Search）：從所有可能的超參數中隨機采樣一部分進行測試。

• 貝葉斯優化（Bayesian Optimization）：利用貝葉斯推斷的思想，通過先前的嘗試結果預測最有可能的最優超參數。

• 遺傳算法（Genetic Algorithm）：模擬自然選擇的過程，用于優化超參數。

（2）集成學習（Ensemble Learning）

通過將多個模型的預測結果結合起來，來提升模型的整體性能。

常見方法有：

• Bagging（如隨機森林）

• Boosting（如XGBoost、LightGBM、CatBoost）

• Stacking：將不同模型的預測作為輸入，使用另一種模型進行預測。

（3）偏差-方差權衡（Bias-Variance Tradeoff）

通過調整模型復雜度，找到偏差和方差之間的平衡，避免過擬合或欠擬合。

（4）正則化技術

• L1 正則化（Lasso）：通過加入L1懲罰項，強迫某些特征的權重變為零，從而起到特征選擇的作用。

• L2 正則化（Ridge）：通過加入L2懲罰項，減小權重的大小，避免某些特征過度影響模型。

• Dropout：常用于深度學習中，在訓練過程中隨機丟棄部分神經元，減少過擬合。

4.2 超參數調優

4.2.1 概念介紹

????????超參數調優是機器學習中的一個關鍵步驟，它通過尋找最優的超參數來提高模型的性能。超參數是指那些在訓練過程中不能通過學習算法自動獲得的參數，它們通常需要由人工設定，比如決策樹的最大深度、SVM的核函數類型、神經網絡的學習率等。其目標是找到一組最優的超參數，使得模型在給定的任務和數據集上表現最好。

4.2.2 方法分類

（1）手動調優：基于經驗和直覺選擇超參數。

（2）網格搜索（Grid Search）：系統地遍歷超參數空間，最常用的一種方法。

（3）隨機搜索（Random Search）：在超參數空間中隨機選擇參數組合進行嘗試

（4）貝葉斯優化（Bayesian Optimization）：基于貝葉斯推理模型，逐步調整超參數。

4.2.3?網格搜索法介紹

網格搜索是一種暴力窮舉法，它通過指定一組超參數的候選值，在這些候選值中進行遍歷，測試每一組超參數組合，選出最優組合。

（1）方法步驟

• 定義超參數空間：為每個超參數選擇一個范圍或集合，通常是多個可能的值。

• 創建所有可能的超參數組合：將每個超參數的可能值組合成一個“網格”。如果有多個超參數，每個超參數的值都會與其它超參數的值組合。

• 模型訓練與評估：對每一組超參數組合，都訓練一個模型，并通過交叉驗證（或其他評估方法）評估模型的性能。

• 選擇最優超參數組合：根據模型的性能指標（如準確率、F1分數等）選擇最優的超參數組合。

（2）優缺點分析

1、優點：

• 簡單直觀：易于實現，理解和應用。
• 確保找到最優解：如果給定的參數空間足夠全面，可以確保找到最優超參數。

2、缺點：

• 計算開銷大：隨著超參數數量和每個超參數的取值范圍增加，網格搜索的計算量呈指數增長。例如，如果有3個超參數，每個有3個候選值，那么需要嘗試27種組合。
• 可能錯過最佳組合：如果超參數空間過于粗糙，可能錯過最佳的超參數組合。

（3）代碼案例

使用KNN算法對scikit-learn的鳶尾花數據集進行分類，使用網格搜索和交叉驗證進行優化。

PS：網格搜索通常會與交叉驗證一起使用，尤其是在數據較少的情況下。交叉驗證通過將數據集分成多個子集，并進行多次訓練和評估，能夠避免過擬合問題，提供更可靠的性能評估。

# 用KNN算法對鳶尾花進行分類，添加網格搜索和交叉驗證
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCVdef knn_iris_gscv():# 1）獲取數據iris = load_iris()# 2）劃分數據集x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)# 3）特征工程：標準化transfer = StandardScaler()x_train = transfer.fit_transform(x_train)x_test = transfer.transform(x_test)# 4）KNN算法預估器, 這里就不傳參數n_neighbors了，交給GridSearchCV來傳遞estimator = KNeighborsClassifier()# 加入網格搜索與交叉驗證, GridSearchCV會讓k分別等于1,2,5,7,9,11進行網格搜索償試。cv=10表示進行10次交叉驗證estimator = GridSearchCV(estimator, param_grid={"n_neighbors": [1, 3, 5, 7, 9, 11]}, cv=10)estimator.fit(x_train, y_train)# 5）模型評估# 方法1：直接比對真實值和預測值y_predict = estimator.predict(x_test)print("y_predict:\n", y_predict)print("直接比對真實值和預測值:\n", y_test == y_predict)# 方法2：計算準確率score = estimator.score(x_test, y_test)print("在測試集中的準確率為：\n", score)  #0.9736842105263158# 最佳參數：best_params_print("最佳參數：\n", estimator.best_params_) #{'n_neighbors': 3}， 說明k=3時最好# 最佳結果：best_score_print("在訓練集中的準確率：\n", estimator.best_score_)  #0.9553030303030303# 最佳估計器：best_estimator_print("最佳估計器:\n", estimator.best_estimator_) # KNeighborsClassifier(n_neighbors=3)# 交叉驗證結果：cv_results_print("交叉驗證過程描述:\n", estimator.cv_results_)#最佳參數組合的索引:最佳k在列表中的下標print("最佳參數組合的索引:\n",estimator.best_index_)#通常情況下，直接使用best_params_更為方便return Noneknn_iris_gscv()