【數據結構】哈希表實現

1. 哈希概念

2 哈希沖突和哈希函數

3. 負載因子

4. 將關鍵字轉為整數

5. 哈希函數

5.1直接定址法

5.2?除法散列法/除留余數法

5.3?乘法散列法（了解）

5.4?全域散列法（了解）

5.5?其他方法（了解）

6. 處理哈希沖突

6.1 開放定址法

線性探測

a.線性探測的問題

開放定址法代碼實現

開放定址法的哈希表結構和查找設計

key不能取模的問題

開放定址法的插入和刪除

擴容

二次探測

雙重散列（了解）

完整代碼實現

6.2?鏈地址法

6.2.1鏈地址法的探討

解決沖突的思路

擴容

6.2.2?鏈地址法代碼實現

極端場景

1. 哈希概念

哈希(hash)又稱散列，是一種組織數據的方式。從譯名來看，有散亂排列的意思。本質就是通過哈希函數把關鍵字Key跟存儲位置建立一個映射關系，查找時通過這個哈希函數計算出Key存儲的位置，進行快速查找。

基于建立映射過程的思考，衍生出來許多方法·，這是下文著重討論的部分，然后數據結構中基于哈希的思想，實現了叫做哈希表（散列表）的數據結構。這里數據結構是數據結構，思想是思想，我們不能直接畫等同

2 哈希沖突和哈希函數

假設我們只有數據范圍是[0, 9999]的N個值，我們要映射到一個M個空間的數組中(一般情況下M >= N)，那么就要借助好的映射方法，使關鍵字key被放到數組的h(key)位置，這里要注意的是h(key)計算出的值必須在[0, M)之間，即數據映射到數組上的位置必須在數組范圍內。這里存在的一個問題就是，兩個不同的key可能會映射到同一個位置去，這種問題我們叫做哈希沖突，或者哈希碰撞。

這里我們把數據與存儲位置之間映射關系的表達式叫做哈希函數(hash function)hf，一個好的哈希函數應該讓N個關鍵字被等概率的均勻的散列分布到哈希表的M個空間中，但是實際中由于數據間沖突無法避免，很難做到等概率設計，但是我們要盡量往這個方向去考量設計。

3. 負載因子

假設哈希表中已經映射存儲了N個值，哈希表的大小為M，那么負載因子 $=\frac{N}{M}$ ，負載因子有些地方也翻譯為載荷因子/裝載因子等，他的英文為load factor。負載因子越大，哈希沖突的概率越高，空間利用率越高；負載因子越小，哈希沖突的概率越低，空間利用率越低；

4. 將關鍵字轉為整數

哈希函數中，我們將關鍵字映射到數組中位置，一般是使用整型做映射計算，如果關鍵字不是整型，我們要想辦法轉換成整型，這個細節我們后面代碼實現中再進行細節展示。下面哈希函數部分我們討論時，如果關鍵字不是整數，那么我們討論的Key是關鍵字轉換成的整數。

5. 哈希函數

在實際的應用中，我們根據具體的哈希函數確定如何映射，求出關鍵字key存放在數組的h(key)位置。反過來說h(key)位置存放的就是key關鍵字，之后查找對應的key數據，我們直接數組下標h(key)就可以找到數據了，因此為了后續根據h(key)再找到數據，插入、查找一系列過程應該使用同一個哈希函數，不能更改，否則算出h(key)前后不一致。

5.1直接定址法

當關鍵字的范圍比較集中時，直接定址法就是非常簡單高效的方法，比如一組關鍵字都在[0,99]之間，那么我們開一個100個數的數組，每個關鍵字的值直接就是存儲位置的下標。

比如一組關鍵字值都在[a,z]的小寫字母，那么我們開一個26個數的數組，每個關鍵字acsii碼-a ascii碼就是存儲位置的下標（這里是通過以a為基準，每個字母映射到數組下標的位置，就是相對a的位置）。

也就是說直接定址法本質就是用關鍵字計算出一個絕對位置或者相對位置。這個方法我們在計數排序部分已經用過了，其次在string章節的下面OJ也用過了。

387. 字符串中的第一個唯一字符 - 力扣（LeetCode）

這題最直接的思路是遍歷每個數來統計出現的次數，如果使用前文的map和set來統計，那么就題目本身來說，使用容器本身的消耗相對較大，沒必要用。

因為只會出現小寫字母，所以我們創建大小為26的數組，根據距離‘a’的距離確定相對位置，26個小寫字母每個都有對應的位置，遍歷字符串，根據對應位置數據確定字母出現次數。

class Solution {
public:int firstUniqChar(string s) {// 每個字母的ascii碼-'a'的ascii碼作為下標映射到count數組，數組中存儲出現的次數int count[26] = { 0 };// 統計次數for (auto ch : s){count[ch - 'a']++;}for (size_t i = 0; i < s.size(); ++i){if (count[s[i] - 'a'] == 1)return i;}return -1;}
};

直接定址法的缺點也非常明顯，直接定址法是根據數據本身的大小或者到最小值的距離來確定絕對/相對位置，當關鍵字的范圍比較分散時，最大值與最小值間的距離就很大，就很浪費內存甚至內存不夠用。

比如最大值與最小值差值達到10億，但是數據本身只有20個數，那么根據最大最小值的距離開辟10大小的數組，但是浪費也基本達到10億。所以對于較分散的數據，我們需要再采取其他數據映射的方式

5.2?除法散列法/除留余數法

? 除法散列法也叫做除留余數法，顧名思義，假設哈希表的大小為M，那么通過key除以M的余數作為映射位置的下標，也就是哈希函數為：h(key) = key % M。

? 當使用除法散列法時，要盡量避免M為某些值，如2的冪，10的冪等。如果是 $2^{X}$ ，那么key % $2^{X}$ 本質相當于保留key二進制形式的后X位，那么后x位相同的值，計算出的哈希值都是一樣的，就沖突了。

如：{63 , 31}看起來沒有關聯的值，如果M是16，也就是 $2^{4}$ ，那么計算出的哈希值都是15，因為63的二進制后8位是 00111111，31的二進制后8位是 00011111。如果是 $10^{X}$ ，就更明顯了，保留的都是10進值的后x位，如：{112, 12312}，如果M是100，也就是 $10^{2}$ ，那么計算出的哈希值都是12。

? 當使用除法散列法時，建議M取不太接近2的整數次冪的一個質數(素數)。

? 需要說明的是，實踐中也是八仙過海，各顯神通，Java的HashMap采用除法散列法時就是2的整數次冪做哈希表的大小M，這樣玩的話，就不用取模，而可以直接位運算，相對而言位運算比模更高效一些。

但是他不是單純的去取模，比如M是2^16次方，本質是取后16位，那么用key’ =key>>16，然后再把key和key' 異或的結果作為哈希值。因為只取后16位，那么后16位相同，數據就會沖突，哈希沖突概念很大，為了避免沖突，我們要采取方式使得每一個數據盡可能具有唯一性，取后16，再取前16位異或，這樣相當于讓原數據的每一數位上的數都參與計算，計算出h(key)。

如果我們M是2^4次方，本質取后4位，這時候前28位是沒利用上的，這時候異或，我們發現如下圖藍色區間的部分是多出來的，如果前28位對應藍色部分二進制形式數位上有不為一處，那么異或之后的h(key)就會超過M，溢出了。

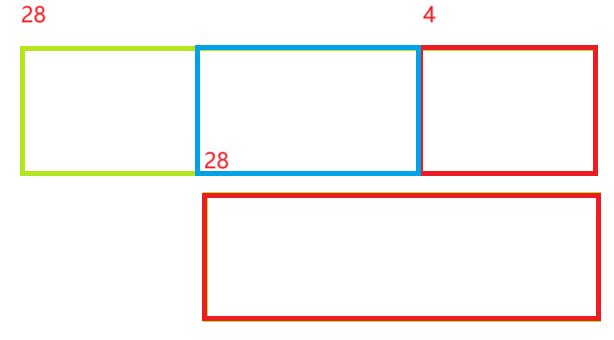
因此對于如下圖這種不對稱的形式，我們要循環取位，每次從28位中取4位出來，與原四位異或，注意的是，我們這里循環按固定數位取數，只是希望讓更多數位加入運算，盡可能使結果獨一無二。

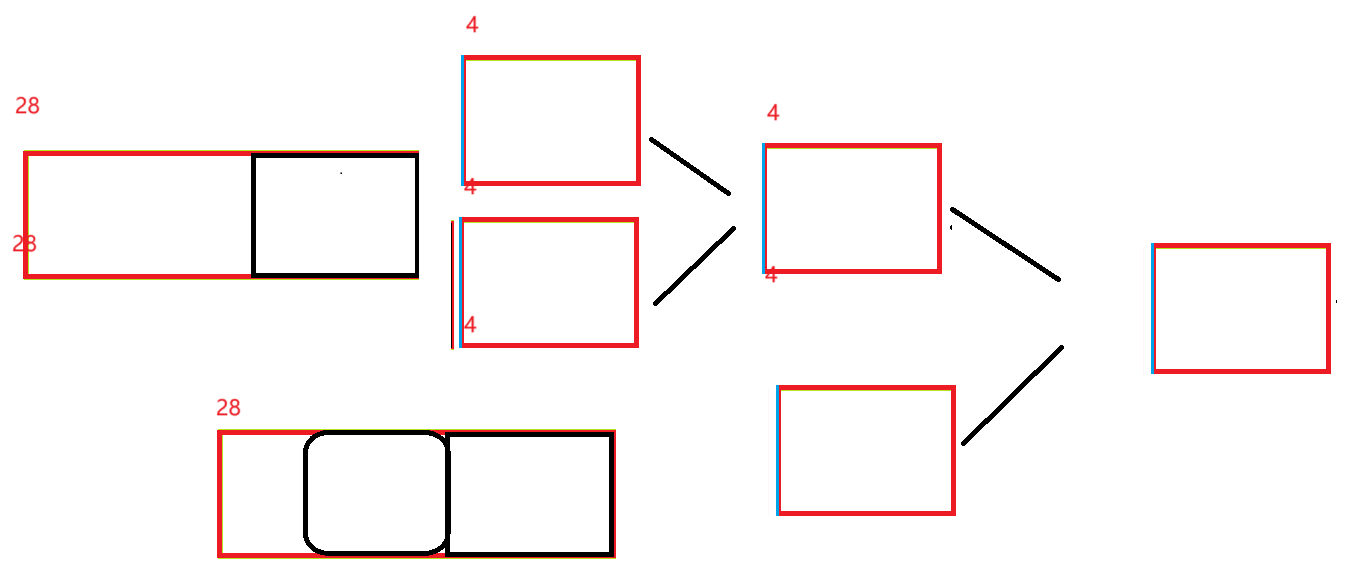
總的來說我們映射出的值還是在[0,M)范圍內，但是通過移位盡量讓key所有的位都參與計算，這樣映射出的哈希值更均勻一些即可。

所以我們上面建議M取不太接近2的整數次冪的一個質數的理論是大多數數據結構書籍中寫的理論，但是實踐中，靈活運用，抓住本質，而不能死讀書。

5.3?乘法散列法（了解）

? 乘法散列法對哈希表大小M沒有要求，他的大思路第一步：用關鍵字 K 乘上常數 A (0<A<1)，并抽取出 k*A 的小數部分。第二步：后再用M乘以k*A 的小數部分，再向下取整。

?h(key) = floor(M × ((A × key)%1.0)) ，其中floor表示對表達式進行下取整，A∈(0,1)，這里最重要的是A的值應該如何設定，Knuth認為A = ( $\sqrt{5}$ ?? 1)/2 = 0.6180339887.... (黃金分割點])比較好，這個數據是經過大量實驗驗證之后的可以使數據分布較為均勻的一種設計。

乘法散列法對哈希表大小M是沒有要求的，假設M為1024，key為1234，A = 0.6180339887, A*key= 762.6539420558，取小數部分為0.6539420558, M×((A×key)%1.0) = 0.6539420558*1024 =669.6366651392，那么h(1234) = 669。

5.4?全域散列法（了解）

基于哈希的各種數據結構被應用到各個領域，比如下圖的分布式集群，我們根據哈希函數來確定數據存儲到哪一臺主機上，使得數據分布均勻存儲，避免大量數據超出某一臺主機存儲上限，以及影響查找數據效率。

但是如果存在一個惡意的對手，他針對我們提供的散列函數，特意構造出一個發生會嚴重沖突的數據集，比如，讓所有關鍵字經過散列函數運算后全部落入同一臺主機上，進而導致嚴重后果。這種情況是可以存在的，只要散列函數是公開且確定的，就可以實現此攻擊。

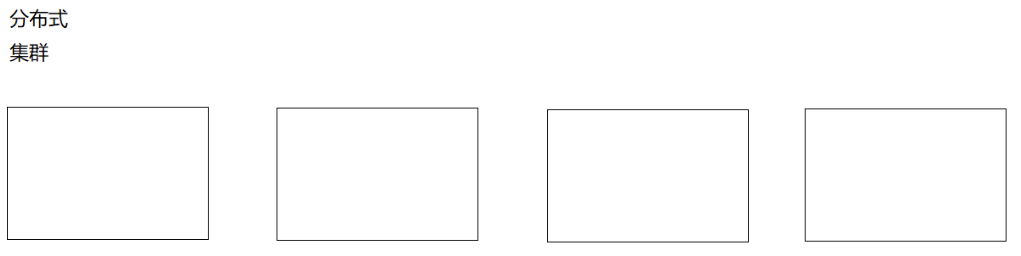
解決方法自然是見招拆招，給散列函數增加隨機性，攻擊者就無法找出確定可以導致最壞情況的數據。這種方法叫做全域散列。

? $h_{ab}$ (key) = ((a × key + b)%P )%M，P需要選一個足夠大的質數，a可以隨機選[1,P-1]之間的任意整數，b可以隨機選[0,P-1]之間的任意整數，這些函數構成了一個P*(P-1)組全域散列函數組（函數組中存放的是不同的哈希函數），然后我們根據隨機選取一個哈希函數進行使用。

假設P=17，M=6，a = 3， b = 4, 則 $h_{34}$ (8) = ((3 × 8 + 4)%17)%6 = 5。那么就從函數組中選取對應的哈希函數，然后使用哈希函數計算h(key)，因為這個哈希函數也是我們通過計算隨機選取的，

這樣惡意分子就無法設計出針對的數據集了。

? 需要注意的是每次初始化哈希表時，隨機選取全域散列函數組中的一個散列函數使用，后續增刪查改都固定使用這個散列函數，否則每次哈希都是隨機選一個散列函數，那么插入是一個散列函數，查找又是另一個散列函數，就會導致找不到插入的key了。

5.5?其他方法（了解）

上面的幾種方法是《算法導論》書籍中講解的方法。

《殷人昆數據結構：用面向對象方法與C++語言描述（第二版）》和《[數據結構(C語言版)].嚴蔚敏_吳偉民》等教材型書籍上面還給出了平方取中法、折疊法、隨機數法、數學分析法等，這些方法相對更適用于一些局限的特定場景，有興趣可以去看看這些書籍。

6. 處理哈希沖突

實踐中哈希表一般還是選擇除法散列法作為哈希函數，當然相對于數據來說，哈希表的M永遠小，永遠都存在兩個不同的數經過計算到了同一位置上，無論選擇什么哈希函數也避免不了沖突，那么插入數據時，如何解決沖突呢？主要有兩種兩種方法，開放定址法和鏈地址法。

6.1 開放定址法

在開放定址法中所有的元素都放到哈希表里，當一個關鍵字key用哈希函數計算出的位置沖突了，則按照某種規則找到一個沒有存儲數據的位置進行存儲，開放定址法中負載因子一定是小于1的。這里的規則有三種：線性探測、二次探測、雙重探測。

線性探測

? 從發生沖突的位置開始，依次線性向后探測，直到尋找到下一個沒有存儲數據的位置為止，如果走到哈希表尾，則回繞到哈希表頭的位置，繼續尋找。

? h(key) = hash0 = key % M, hash0位置沖突了，則線性探測公式為： $h_{c}$ (key, i) = hashi = (hash0 + i) % M， i = {1, 2, 3, ..., M ? 1}，因為負載因子小于1（存在空位），則最多探測M-1次，一定能找到一個存儲key的位置。

a.線性探測的問題

線性探測的比較簡單且容易實現，線性探測的問題是目前有多個值映射到哈希表的同一位置，假設hash0位置連續沖突，第一個沖突值向后找到空的hash1位置存放，第二個沖突值向后找到空的hash2位置存儲數據，我們發現之前沖突的多個數據會搶占之后數據的存儲位置，那么之后的數據就要從被搶占的位置向后不斷遍歷找到空位置，也就是說空位置越少，找到空位置需要遍歷的次數就越多，效率越低，所以實際中一般我們會保持負載因子小于0.7，負載因子大于0.7則進行擴容。

hash0，hash1，hash2位置已經存儲數據了，后續映射到hash0，hash1，hash2，hash3的值都會爭奪hash3位置，這種現象叫做群集/堆積。下面的二次探測可以一定程度改善這個問題。

下面演示 {19,30,5,36,13,20,21,12} 等這一組值映射到M=11的表中。

h(19) = 8，h(30) = 8，h(5) = 5，h(36) = 3，h(13) = 2，h(20) = 9，h(21) =10，h(12) = 1

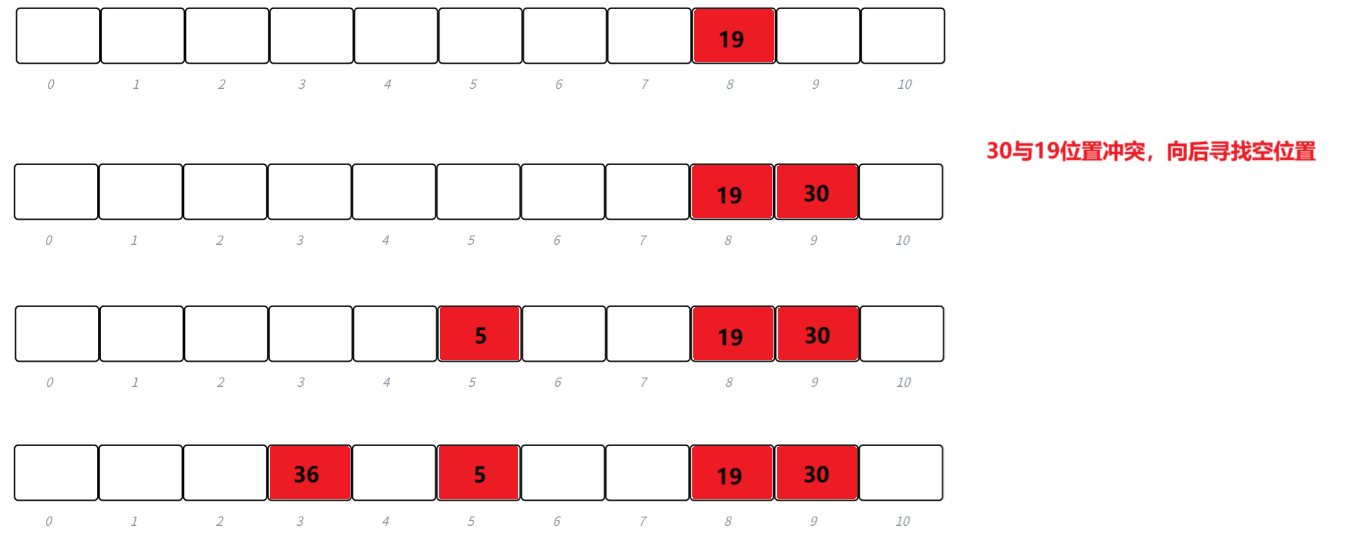
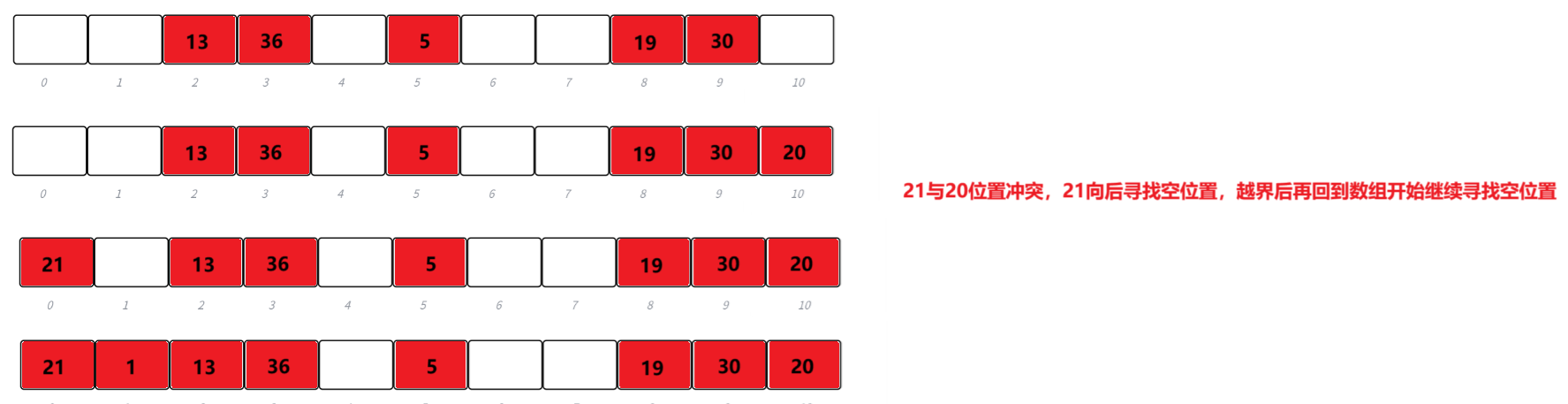
開放定址法代碼實現

開放定址法在實踐中，不如下面講的鏈地址法，因為開放定址法解決沖突不管使用哪種方法，占用的都是哈希表中的空間，數據之間相互競爭空間，始終存在互相影響的問題。再考慮到線性探測較為簡單，所以開放定址法，我們選擇線性探測的實現來詳細說明開放定制法的各項細節。

開放定址法的哈希表結構和查找設計

enum State
{EXIST,EMPTY,DELETE
};
template<class K, class V>
struct HashData
{pair<K, V> _kv;State _state = EMPTY;
};
template<class K, class V>
class HashTable
{
private:vector<HashData<K, V>> _tables;size_t _n = 0; // 表中存儲數據個數
};

我們這里底層封裝vector來存儲數據，要注意的是，因為查找需要找到空位置，所以這里需要給每個存儲值的位置加一個狀態標識，狀態表示需要有存在、空、刪除三種狀態，否則刪除一些值以后，會影響后面沖突的值的查找。

如下圖，我們刪除30，30映射的位置就變空了，那么我們查找20時，因為線性探測的邏輯是沖突了，就往后找空位存放，反過來說如果找到空位置了，那空位置之后一定也是空的，沒有數據，所以如果我們查找20，那么查找到第9位為空，就不會繼續往后查了，導致查找20失敗。

當我們給每個位置加一個狀態標識{EXIST,EMPTY,DELETE} ，刪除30就可以不用刪除值，而是把狀態改為DELETE ，那么查找20時是遇到EMPTY 才能停，我們就可以找到20了。

h(19) = 8，h(30) = 8，h(5) = 5，h(36) = 3，h(13) = 2，h(20) = 9，h(21) =10，h(12) = 1

		HashData<K, V>* Find(const K& key){Hash hs;size_t hashi = hs(key) % _tables.size();//哈希函數while (_tables[hashi]._state != EMPTY){if (_tables[hashi]._state == EXIST&& _tables[hashi]._kv.first == key)//當前位置存在數據，且數據與目標值相等，說明找到數據{return &_tables[hashi];}++hashi;//不在當前位置就繼續往后找hashi %= _tables.size();}return nullptr;}

key不能取模的問題

當key是string/Date等類型時，key不能取模，那么我們需要給HashTable增加一個仿函數，

這個仿函數支持把key轉換成一個可以取模的整形。這樣這個key就與轉換后的整形存在一層映射關系，然后這個轉換后的整形由于哈希表存在映射關系，間接的，key就與哈希表存在映射關系了。

如果key可以轉換為整形并且不容易沖突，那么這個仿函數就用默認參數即可（默認的仿函數，我們使用強轉即可），如果這個Key不能轉換為整形，我們就需要自己實現一個仿函數傳給這個參數，實現這個仿函數的要求就是盡量key的每值都參與到計算中，讓不同的key轉換出的整形值不同。

由于string做哈希表的key非常常見，所以STL庫中unordered系列使用不需要我們傳遞仿函數，就是因為針對string類型特化了。

針對string類型的轉換，方式有很多種，比如講string中的每個字符加起來得到一個整形值，但這種方式容易出現字符一致、但字符順序不一致字符串沖突。

經過科學家的大量實驗研究，發現可以如下圖，將字符串挨個取出，乘上某個固定數，再與下個字符相加，再乘上固定數…………直到結束，由于不同字母的ASCII不同，那乘固定數的結果就不同，這樣字符串映射沖突的可能性就大大降低了。

template<class K>
struct HashFunc
{size_t operator()(const K& key){return (size_t)key;}
};
// 特化
template<>
struct HashFunc<string>
{// 字符串轉換成整形，可以把字符ascii碼相加即可// 但是直接相加的話，類似"abcd"和"bcad"這樣的字符串計算出是相同的// 這里我們使用BKDR哈希的思路，用上次的計算結果去乘以一個質數，這個質數一般去31, 131//等效果會比較好size_t operator()(const string& key){size_t hash = 0;for (auto e : key){hash *= 131;hash += e;}return hash;}
};
template<class K, class V, class Hash = HashFunc<K>>
class HashTable
{
public:
private:vector<HashData<K, V>> _tables;size_t _n = 0; // 表中存儲數據個數
};

開放定址法的插入和刪除

template<class K>
struct HashFunc//針對可以轉換成整形的數據
{size_t operator()(const K& key){return (size_t)key;//如浮點數、字符等}
};// 特化
template<>
struct HashFunc<string>
{size_t operator()(const string& key){size_t hash = 0;for (auto e : key){hash *= 31;hash += e;}return hash;}
};namespace open_address
{enum State{EXIST,EMPTY,DELETE};template<class K, class V>struct HashData{pair<K, V> _kv;State _state = EMPTY;};template<class K, class V, class Hash = HashFunc<K>>class HashTable{public:HashTable(){_tables.resize(10);}bool Insert(const pair<K, V>& kv){if (Find(kv.first))return false;// 負載因子控制在0.7以下，超過0.7，效率較低，需要擴容//通過*10，避免出現浮點數比較if (_n * 10 / _tables.size() >= 7){//vector<HashData<K, V>> newTables(_tables.size() * 2);//// 遍歷舊表， 將所有數據映射到新表//// ...//_tables.swap(newTables);HashTable<K, V, Hash> newHT;newHT._tables.resize(_tables.size() * 2);for (size_t i = 0; i < _tables.size(); i++){if (_tables[i]._state == EXIST){//復用代碼，重新映射到新表中newHT.Insert(_tables[i]._kv);}}//直接舊表與新表的底層容器交換，效率較高_tables.swap(newHT._tables);}Hash hs;size_t hashi = hs(kv.first) % _tables.size();while (_tables[hashi]._state == EXIST){++hashi;hashi %= _tables.size();}_tables[hashi]._kv = kv;_tables[hashi]._state = EXIST;++_n;return true;}bool Erase(const K& key){HashData<K, V>* ret = Find(key);if (ret == nullptr)//當前位置為空，也意味著之后沒有數據了{return false;}else{ret->_state = DELETE;return true;}}private:vector<HashData<K, V>> _tables;size_t _n = 0;  // 表中存儲數據個數};

// 對key為int的鍵值對測試void TestHT1(){HashTable<int, int> ht;int a[] = { 11,21,4,14,24,15,9 };for (auto e : a){ht.Insert({ e,e });}ht.Insert({ 19,19 });ht.Insert({ 19,190 });ht.Insert({ 19,1900 });ht.Insert({ 39,1900 });cout << ht.Find(24) << endl;ht.Erase(4);cout << ht.Find(24) << endl;cout << ht.Find(4) << endl;}// 字符串轉整形處理方式struct StringHashFunc{size_t operator()(const string& s){size_t hash = 0;for (auto e : s){hash *= 31;hash += e;}return hash;}};// 對key為string類型鍵值對進行測試void TestHT2(){HashTable<string, string> ht;ht.Insert({ "sort", "排序" });ht.Insert({ "left", "左邊" });//string s1("sort");//string s2("sort");cout << StringHashFunc()("bacd") << endl;cout << StringHashFunc()("abcd") << endl;cout << StringHashFunc()("aadd") << endl;}
}

擴容

這里我們哈希表負載因子控制在0.7，當負載因子到0.7以后我們就需要擴容了，我們還是按照2倍擴容（簡單點）。

之前文章中我們講過擴容一般來說擴容兩倍左右為宜，但是同時我們要保持哈希表大小是一個質數，第一個是質數，2倍后就不是質數了。那么如何解決了，一種方案就是上面1.4.1除法散列中我們講的Java HashMap的使用2的整數冪，但是計算時不能直接取模的改進方法。

另外一種方案是sgi版本的哈希表使用的方法，給了一個近似2倍的質數表，每次去質數表獲取擴容后的大小。

inline unsigned long __stl_next_prime(unsigned long n)
{// Note: assumes long is at least 32 bits.static const int __stl_num_primes = 28;static const unsigned long __stl_prime_list[__stl_num_primes] ={53, 97, 193, 389, 769,1543, 3079, 6151, 12289, 24593,49157, 98317, 196613, 393241, 786433,1572869, 3145739, 6291469, 12582917, 25165843,50331653, 100663319, 201326611, 402653189, 805306457,1610612741, 3221225473, 4294967291};const unsigned long* first = __stl_prime_list;const unsigned long* last = __stl_prime_list + __stl_num_primes;const unsigned long* pos = lower_bound(first, last, n);return pos == last ? *(last - 1) : *pos;
}

二次探測

? 從發生沖突的位置開始，依次左右按二次方跳躍式探測，直到尋找到下一個沒有存儲數據的位置為止，如果往右走到哈希表尾，則回繞到哈希表頭的位置；如果往左走到哈希表頭，則回繞到哈希表尾的位置；

? h(key) = hash0 = key % M, hash0位置沖突了，則二次探測公式為：

$h_{c}$ (key, i) = hashi = (hash0 ± $i^{2}$ ) % M， i = {1, 2, 3, ..., $\frac{M}{2}$ }

? 二次探測當 hashi = (hash0 ? $i^{2}$ )%M 時，當hashi<0時，需要hashi += M，是映射位置繞回到哈希表內。

? 下面?{19,30,52,63,11,22} 等這一組值映射到M=11的表中。

h(19) = 8, h(30) = 8, h(52) = 8, h(63) = 8, h(11) = 0, h(22) = 0

雙重散列（了解）

? 第一個哈希函數計算出的值發生沖突，使用第二個哈希函數計算出一個跟key相關的偏移量值，不斷往后探測，直到尋找到下一個沒有存儲數據的位置為止。本質來說雙重散列是通過跳躍映射來減少沖突堆積。

? , hash0位置沖突了，則雙重探測公式為： $h_{1}$ (key) = hash0 = key % M， $h_{c}$ (key, i) = hashi = (hash0 + i ? $h_{2}$ (key)) % M， i = {1, 2, 3, ...,M}

? 要求 $h_{2}$ (key) < M )且 $h_{2}$ (key)和M互為質數，有兩種簡單的取值方法：1、當M為2整數冪時， $h_{2}$ (key)從[0，M-1]任選一個奇數；2、當M為質數時， $h_{2}$ (key) = key % (M ? 1) + 1

? 保證 $h_{2}$ (key)與M互質是因為根據固定的偏移量所尋址的所有位置將形成一個群，映射范圍固定在這個群眾，若最大公約數p = gcd(M, $h_{1}$ (key)) > 1，那么所能尋址的位置的個數為 M/P < M，使得對于一個關鍵字來說無法充分利用整個散列表。舉例來說，若初始探查位置為1，偏移量為3，整個散列表大小為12，那么所能尋址的位置固定在為{1, 4, 7, 10}，尋址個數為12/gcd(12, 3) = 4

? 下面?{19,30,52,74} 等這一組值映射到M=11的表中，設 $h_{2}$ (key) = key%10 + 1

完整代碼實現

namespace open_address
{enum State{EXIST,EMPTY,DELETE};template<class K, class V>struct HashData{pair<K, V> _kv;State _state = EMPTY;};template<class K, class V, class Hash = HashFunc<K>>class HashTable{public:inline unsigned long __stl_next_prime(unsigned long n){// Note: assumes long is at least 32 bits.static const int __stl_num_primes = 28;static const unsigned long __stl_prime_list[__stl_num_primes] ={53, 97, 193, 389, 769,1543, 3079, 6151, 12289, 24593,49157, 98317, 196613, 393241, 786433,1572869, 3145739, 6291469, 12582917, 25165843,50331653, 100663319, 201326611, 402653189, 805306457,1610612741, 3221225473, 4294967291};const unsigned long* first = __stl_prime_list;const unsigned long* last = __stl_prime_list +__stl_num_primes;const unsigned long* pos = lower_bound(first, last, n);return pos == last ? *(last - 1) : *pos;}HashTable(){_tables.resize(__stl_next_prime(0));}bool Insert(const pair<K, V>& kv){if (Find(kv.first))return false;// 負載因子大于0.7就擴容if (_n * 10 / _tables.size() >= 7){// 這里利用類似深拷貝現代寫法的思想插入后交換解決HashTable<K, V, Hash> newHT;newHT._tables.resize(__stl_next_prime(_tables.size() + 1));for (size_t i = 0; i < _tables.size(); i++){if (_tables[i]._state == EXIST){newHT.Insert(_tables[i]._kv);}}_tables.swap(newHT._tables);}Hash hash;size_t hash0 = hash(kv.first) % _tables.size();size_t hashi = hash0;size_t i = 1;while (_tables[hashi]._state == EXIST){// 線性探測hashi = (hash0 + i) % _tables.size();// 二次探測就變成 +- i^2++i;}_tables[hashi]._kv = kv;_tables[hashi]._state = EXIST;++_n;return true;}HashData<K, V>* Find(const K& key){Hash hash;size_t hash0 = hash(key) % _tables.size();size_t hashi = hash0;size_t i = 1;while (_tables[hashi]._state != EMPTY){if (_tables[hashi]._state == EXIST&& _tables[hashi]._kv.first == key){return &_tables[hashi];}// 線性探測hashi = (hash0 + i) % _tables.size();++i;}return nullptr;}bool Erase(const K& key){HashData<K, V>* ret = Find(key);if (ret == nullptr){return false;}else{ret->_state = DELETE;--_n;return true;}}private:vector<HashData<K, V>> _tables;size_t _n = 0; // 表中存儲數據個數};
}

6.2?鏈地址法

6.2.1鏈地址法的探討

解決沖突的思路

開放定址法中所有的元素都放到哈希表里，不管怎么處理數據都存在互相競爭同一塊空間的可能性。

而鏈地址法中所有的數據不再直接存儲在哈希表中，哈希表中存儲一個指針，沒有數據映射這個位置時，這個指針為空，有多個數據映射到這個位置時，我們把這些沖突的數據鏈接成一個鏈表，掛在哈希表這個位置下面，鏈地址法也叫做拉鏈法或者哈希桶。

? 下面?{19,30,5,36,13,20,21,12,24,96} 等這一組值映射到M=11的表中。

h(19) = 8，h(30) = 8，h(5) = 5，h(36) = 3，h(13) = 2，h(20) = 9，h(21) =10，h(12) = 1,h(24) = 2,h(96) = 88

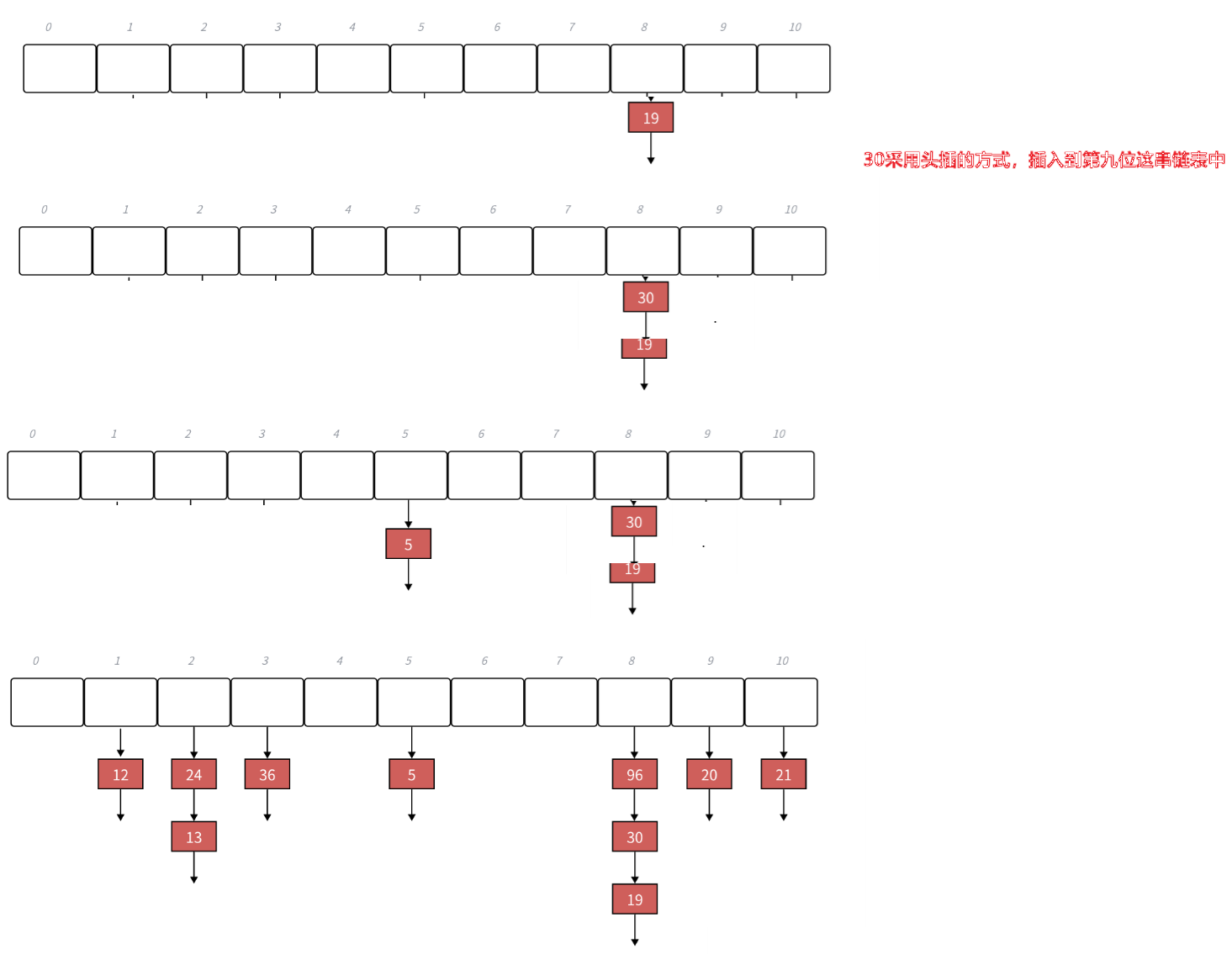
擴容

開放定址法負載因子必須小于1，鏈地址法的負載因子就沒有限制了，可以大于1，但是過多因子過大也會導致單個數據鏈過長，效率也會損失。

所以總的來說負載因子越大，哈希沖突的概率越高，空間利用率越高；負載因子越小，哈希沖突的概率越低，空間利用率越低；stl中unordered_xxx的最大負載因子基本控制在1，大于1就擴容，我們下面實現也使用這個方式。

6.2.2?鏈地址法代碼實現

鏈地址法與開放定址法不同是會開辟出節點，因此實現過程中涉及到拷貝（深拷貝）、析構等情況，我們需要自己實現相關函數，處理好資源

namespace hash_bucket
{template<class K, class V>struct HashNode{pair<K, V> _kv;HashNode<K, V>* _next;HashNode(const pair<K, V>& kv):_kv(kv), _next(nullptr){}};//sgi版本的哈希表使用的方法，給了一個近似2倍的質數表，每次去質數表獲取擴容后的大小template<class K, class V, class Hash = HashFunc<K>>class HashTable{typedef HashNode<K, V> Node;inline unsigned long __stl_next_prime(unsigned long n){static const int __stl_num_primes = 28;static const unsigned long __stl_prime_list[__stl_num_primes] ={53, 97, 193, 389, 769,1543, 3079, 6151, 12289, 24593,49157, 98317, 196613, 393241, 786433,1572869, 3145739, 6291469, 12582917, 25165843,50331653, 100663319, 201326611, 402653189, 805306457,1610612741, 3221225473, 4294967291};const unsigned long* first = __stl_prime_list;const unsigned long* last = __stl_prime_list +__stl_num_primes;const unsigned long* pos = lower_bound(first, last, n);return pos == last ? *(last - 1) : *pos;}public:HashTable(){_tables.resize(__stl_next_prime(0), nullptr);}// 拷貝構造和賦值拷貝需要實現深拷貝，有興趣的讀者可以自行實現~HashTable(){// 依次把每個桶釋放for (size_t i = 0; i < _tables.size(); i++){Node* cur = _tables[i];while (cur){Node* next = cur->_next;delete cur;cur = next;}_tables[i] = nullptr;}}bool Insert(const pair<K, V>& kv){Hash hs;size_t hashi = hs(kv.first) % _tables.size();// 負載因子==1擴容if (_n == _tables.size()){/*HashTable<K, V> newHT;newHT._tables.resize(__stl_next_prime(_tables.size()+1);for (size_t i = 0; i < _tables.size(); i++){Node* cur = _tables[i];while(cur){newHT.Insert(cur->_kv);cur = cur->_next;}}_tables.swap(newHT._tables);*/// 這里如果使用上面的方法，擴容時創建新的結點，后面還要使用舊結點，浪費了// 下面的方法，直接移動舊表的結點到新表，效率更好vector<Node*>newtables(__stl_next_prime(_tables.size() + 1), nullptr);for (size_t i = 0; i < _tables.size(); i++){Node* cur = _tables[i];while (cur){Node* next = cur->_next;// 舊表中節點，挪動新表重新映射的位置size_t hashi = hs(cur->_kv.first) % newtables.size();// 頭插到新表cur->_next = newtables[hashi];newtables[hashi] = cur;cur = next;}_tables[i] = nullptr;}_tables.swap(newtables);}// 頭插(尾插的話鏈表不方便找到尾節點，所以采用頭插的方式)Node* newnode = new Node(kv);newnode->_next = _tables[hashi];_tables[hashi] = newnode;++_n;return true;}Node* Find(const K& key){Hash hs;size_t hashi = hs(key) % _tables.size();Node* cur = _tables[hashi];while (cur){if (cur->_kv.first == key){return cur;}cur = cur->_next;}return nullptr;}bool Erase(const K& key){Hash hs;size_t hashi = hs(key) % _tables.size();Node* prev = nullptr;Node* cur = _tables[hashi];while (cur){if (cur->_kv.first == key){if (prev == nullptr){_tables[hashi] = cur->_next;}else{prev->_next = cur->_next;}delete cur;--_n;return true;}prev = cur;cur = cur->_next;}return false;}private:vector<Node*> _tables; // 指針數組size_t _n = 0; // 表中存儲數據個數};
}

極端場景

那如果極端場景下，某個桶特別長怎么辦？其實我們可以考慮使用全域散列法，這樣就不容易被針對了。但是假設不是被針對了，偶然情況下，某個桶很長，查找效率很低怎么辦？這里介紹在Java8的HashMap中，當桶的長度超過一定閥值(8)時就把鏈表轉換成紅黑樹。一般情況下，不斷擴容，單個桶很長的場景還是比較少的，下面我們實現就不搞這么復雜了，這個解決極端場景的思路，大家了解一下。