霍夫變換詳解與代碼示例

霍夫變換（Hough Transform）是一種用于檢測圖像中幾何形狀（如直線、圓）的特征提取技術。其核心思想是將圖像空間中的點映射到參數空間（霍夫空間），通過累積投票機制識別形狀。下面我將逐步推導原理、解釋霍夫空間、詳述直線和圓檢測，并提供Python代碼示例（使用OpenCV庫）。

---

1. 霍夫變換原理

霍夫變換基于參數化思想：圖像空間中的點對應霍夫空間中的曲線，而霍夫空間中的峰值對應圖像中的幾何形狀。

• 基本推導（以直線為例）：
  • 圖像空間中，一條直線可表示為 $y=mx+c$，但此形式在垂直線時斜率 $m$ 無限大，不實用。改用極坐標方程：
    $$\rho =x\cos \theta +y\sin \theta$$
    其中：
    • $\rho$ 是原點到直線的垂直距離（$\rho \ge 0$），
    • $\theta$ 是直線與x軸的夾角（$0\le \theta <180^{°}$）。

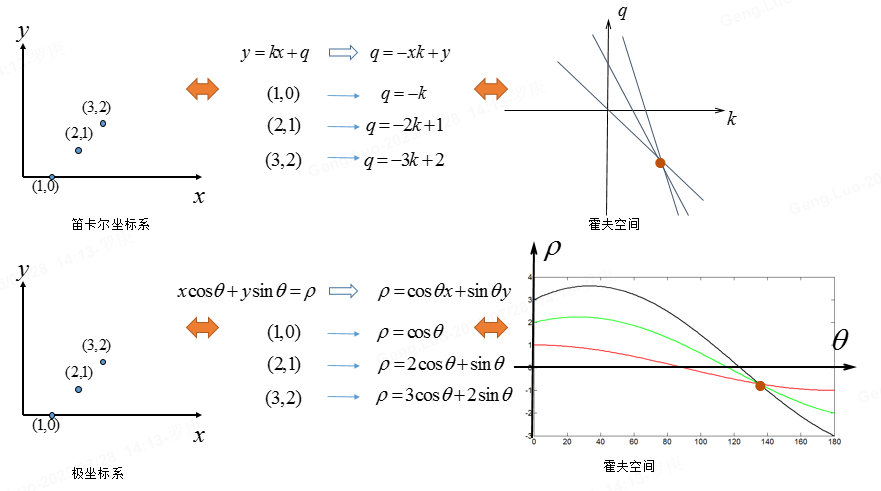
• 圖像空間中每個點 $(x_i,y_i)$ 對應霍夫空間中的一條正弦曲線：$\rho =x_i\cos \theta +y_i\sin \theta$。

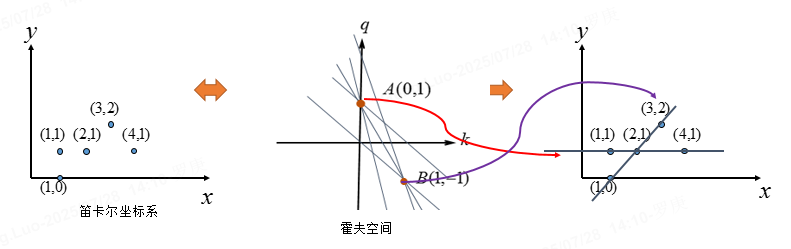
• 多個點共線時，它們在霍夫空間中的曲線相交于一點 $({\theta }_k,{\rho }_k)$，該點即為直線參數。

• 累積投票：將霍夫空間離散化為網格（累加器數組），每個點 $(x_i,y_i)$ 對所有可能的 $\theta$ 計算 $\rho$，并在對應網格單元投票。峰值單元對應檢測到的直線。
  

• 通用原理：

  • 適用于任意參數化形狀（如圓、橢圓）。
  • 優點：對噪聲和部分遮擋魯棒；缺點：計算復雜度隨參數維度增加（如直線是二維，圓是三維）。

---

2. 霍夫空間

霍夫空間是參數空間，用于累積投票：

• 定義：圖像空間中的點映射到參數空間中的曲線或曲面。
• 量化：
  • $\theta$ 范圍：$0$ 到 $180^{°}$（或 $0$ 到 $\pi$ 弧度），通常離散為 $1^{°}$ 步長。
  • $\rho$ 范圍：$?D$ 到 $D$（$D$ 為圖像對角線長度），離散為整數步長（如1像素）。
• 累加器：二維數組 $A[\theta ][\rho ]$，初始為0。每個邊緣點增加通過它的所有可能直線的投票數。峰值 $A[{\theta }_k][{\rho }_k]$ 表示檢測結果。

---

3. 霍夫直線檢測

基于上述原理，檢測圖像中的直線：

• 步驟：

  1. 邊緣檢測：預處理圖像（如Canny邊緣檢測），獲取二值邊緣圖。
  2. 映射到霍夫空間：對每個邊緣點 $(x_i,y_i)$，遍歷 $\theta$（例如 $\theta =0^{°},1^{°},\dots ,179^{°}$），計算 $\rho =x_i\cos \theta +y_i\sin \theta$，并累加 $A[\theta ][\rho ]$。
  3. 找峰值：設定閾值，$A[\theta ][\rho ]>\text{閾值}$ 的單元對應檢測到的直線。
  4. 轉換回圖像空間：用 $({\theta }_k,{\rho }_k)$ 繪制直線 ${\rho }_k=x\cos {\theta }_k+y\sin {\theta }_k$。

• 優化：使用概率霍夫變換（Probabilistic Hough Transform），隨機采樣邊緣點，減少計算量。

---

4. 霍夫圓檢測

圓檢測擴展了霍夫變換到三維參數空間：

• 圓方程：圓心 $(a,b)$，半徑 $r$，方程為：
  $$(x?a{)}^2+(y?b{)}^2=r^2$$
• 霍夫空間：三維空間 $(a,b,r)$。
• 步驟：
  1. 邊緣檢測：獲取邊緣圖。
  2. 梯度優化：利用邊緣梯度方向減少計算：
     • 邊緣點 $(x_i,y_i)$ 的梯度方向 $?$ 近似圓心方向。
     • 對每個邊緣點，沿梯度方向 $?$ 和 $?+180^{°}$，在可能半徑 $r$ 范圍內計算圓心 $(a,b)$：
       $$a=x_i?r\cos ?,b=y_i?r\sin ?$$
     • 累加三維累加器 $A[a][b][r]$。
  3. 找峰值：設定閾值，$A[a][b][r]>\text{閾值}$ 的單元對應檢測到的圓。
• 挑戰：三維空間計算量大，常使用多尺度或梯度方法優化。

---

5. 代碼示例

使用Python和OpenCV實現霍夫直線和圓檢測。需安裝OpenCV：pip install opencv-python。

(a) 霍夫直線檢測代碼

import cv2
import numpy as np
import matplotlib.pyplot as plt# 讀取圖像并轉換為灰度
image = cv2.imread('input.jpg')  # 替換為您的圖像路徑
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)# 邊緣檢測（Canny）
edges = cv2.Canny(gray, 50, 150)  # 閾值50和150# 霍夫直線變換
# 參數：邊緣圖, rho精度(1像素), theta精度(1度), 閾值(投票數)
lines = cv2.HoughLines(edges, 1, np.pi / 180, 150)  # 閾值調整以控制檢測靈敏度# 繪制檢測到的直線
if lines is not None:for line in lines:rho, theta = line[0]a = np.cos(theta)b = np.sin(theta)x0 = a * rhoy0 = b * rho# 計算直線端點x1 = int(x0 + 1000 * (-b))y1 = int(y0 + 1000 * (a))x2 = int(x0 - 1000 * (-b))y2 = int(y0 - 1000 * (a))cv2.line(image, (x1, y1), (x2, y2), (0, 0, 255), 2)  # 紅色直線# 顯示結果
plt.imshow(cv2.cvtColor(image, cv2.COLOR_BGR2RGB))
plt.title('霍夫直線檢測')
plt.axis('off')
plt.show()

(b) 霍夫圓檢測代碼

import cv2
import numpy as np
import matplotlib.pyplot as plt# 讀取圖像并轉換為灰度
image = cv2.imread('input.jpg')  # 替換為您的圖像路徑
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
gray = cv2.medianBlur(gray, 5)  # 中值濾波去噪# 霍夫圓變換
# 參數：輸入圖, 方法(HOUGH_GRADIENT), dp=1(累加器分辨率), minDist(圓心最小距離), param1(Canny高閾值), param2(累加器閾值), minRadius, maxRadius
circles = cv2.HoughCircles(gray, cv2.HOUGH_GRADIENT, dp=1, minDist=50,param1=50, param2=30, minRadius=10, maxRadius=100)# 繪制檢測到的圓
if circles is not None:circles = np.uint16(np.around(circles))for circle in circles[0, :]:center = (circle[0], circle[1])  # 圓心radius = circle[2]  # 半徑cv2.circle(image, center, radius, (0, 255, 0), 2)  # 綠色圓cv2.circle(image, center, 2, (0, 0, 255), 3)  # 圓心紅點# 顯示結果
plt.imshow(cv2.cvtColor(image, cv2.COLOR_BGR2RGB))
plt.title('霍夫圓檢測')
plt.axis('off')
plt.show()

代碼說明：

• 輸入圖像：替換 'input.jpg' 為您的圖像路徑（確保圖像有清晰邊緣）。
• 參數調整：
  • 直線檢測：cv2.HoughLines 的閾值控制最少投票數（值越大，檢測越嚴格）。
  • 圓檢測：param2 是關鍵閾值（值越小，檢測越多圓，但噪聲增加）。
• 輸出：顯示原圖疊加檢測結果（直線為紅色，圓為綠色帶圓心紅點）。
• 優化：實際應用中，可結合圖像預處理（如高斯模糊）提高準確性。

霍夫變換是計算機視覺基礎工具，廣泛應用于車道檢測、工業質檢等領域。通過調整參數和優化方法，可平衡精度與效率。

總結

霍夫變換通過將圖像空間映射到參數空間，有效檢測幾何形狀。其核心是累加器投票機制，在霍夫空間中識別峰值。本示例展示了直線檢測的實現，可擴展到其他形狀（如圓）。實際使用時，建議結合圖像優化（如降采樣）以提高效率。如果您有特定圖像或擴展需求，我可以進一步調整代碼！