一、混淆矩陣
混淆矩陣是機器學習中評估分類模型性能的重要工具,尤其適用于二分類或多分類任務。它通過展示模型預測結果與實際標簽的匹配情況,幫助理解模型的錯誤類型(如假陽性、假陰性等)。以下通過二分類場景為例,結合圖示和概念解析混淆矩陣的核心內容。
一、二分類混淆矩陣基礎結構
二分類問題中,數據標簽只有兩類(通常稱為 “正類” 和 “負類”),混淆矩陣為?2×2 矩陣,結構如下:
| 實際標簽 \ 預測標簽 | 預測為正類(Positive) | 預測為負類(Negative) |
|---|---|---|
| 實際為正類(Positive) | 真正例(TP) | 假負例(FN) |
| 實際為負類(Negative) | 假正例(FP) | 真負例(TN) |
二、核心概念與圖示說明
為更直觀理解,我們用一個場景舉例:假設模型用于預測 “是否患癌癥”,其中 “患癌癥” 為正類(P),“未患癌癥” 為負類(N)。
真正例(True Positive, TP)
- 實際標簽為正類(確實患癌癥),模型預測也為正類(正確預測患病)。
- 例:病人確實得了癌癥,模型判斷為 “患病”。
假負例(False Negative, FN)
- 實際標簽為正類(確實患癌癥),但模型預測為負類(錯誤預測為未患病)。
- 例:病人得了癌癥,模型卻判斷為 “未患病”(漏診)。
假正例(False Positive, FP)
- 實際標簽為負類(未患癌癥),但模型預測為正類(錯誤預測為患病)。
- 例:病人沒患癌癥,模型卻判斷為 “患病”(誤診)。
真負例(True Negative, TN)
- 實際標簽為負類(未患癌癥),模型預測也為負類(正確預測未患病)。
- 例:病人確實沒患癌癥,模型判斷為 “未患病”。
三、從混淆矩陣衍生的關鍵指標
混淆矩陣的價值不僅在于展示錯誤分布,更能通過這些數值計算模型性能指標:
| 指標 | 計算公式 | 含義(以癌癥預測為例) |
|---|---|---|
| 準確率(Accuracy) | (TP+TN)/(TP+TN+FP+FN) | 整體預測正確的比例(所有判斷對的樣本占比) |
| 精確率(Precision) | TP/(TP+FP) | 預測為正的樣本中,實際真為正的比例(避免誤診) |
| 召回率(Recall) | TP/(TP+FN) | 實際為正的樣本中,被正確預測的比例(避免漏診) |
| F1 分數 | 2×(Precision×Recall)/(Precision+Recall) | 精確率和召回率的調和平均, |
還有多分類混淆矩陣就不介紹了,原理相同
用這個混淆舉證是方便看代碼的優化效果
二、正則化懲罰
正則化是機器學習中防止模型 “學過頭”(過擬合)的技術,通過 “懲罰復雜模型” 讓模型更簡單、更通用。以下用圖示和例子通俗講解。
1、為什么需要正則化?—— 過擬合的問題
當模型太復雜(比如參數太多),會 “死記硬背” 訓練數據里的細節甚至噪聲,導致:
- 訓練時表現極好(擬合了所有細節);
- 遇到新數據時表現很差(無法通用)。
直觀對比圖:
數據點(帶噪聲)→ ● ● ● ● ●
真實規律 → ───────(簡單直線) 無正則化的模型 → ╲╱╲╱╲╱(曲線扭曲,貼合每個點,過擬合)
有正則化的模型 → ───────(曲線平滑,接近真實規律,泛化好) 正則化的作用:給復雜模型 “降復雜度”,讓它別太糾結訓練數據的細節。
2、正則化怎么工作?—— 給參數 “減肥”
模型的預測能力來自 “參數”(類似公式里的系數)。參數越大、數量越多,模型越復雜。
正則化通過 “懲罰大參數”,讓參數值變小或變少,從而簡化模型。
形象比喻:
- 把模型比作 “學生”,訓練數據是 “課本”,測試數據是 “考試”。
- 過擬合的學生:死記硬背課本里的每個字(包括錯別字),考試換題型就不會了。
- 正則化:要求學生 “理解核心原理”(參數簡化),別死記細節,考試時更能靈活應對。
3、常見的兩種正則化(圖示對比)
1. L2 正則化:讓參數 “變瘦”
- 效果:讓所有參數的數值都變小(但很少變成 0),就像給參數 “整體減肥”,讓模型更 “穩健”。
- 圖示:
無正則化 → 參數值:[10, 8, -7](數值大,模型敏感) L2正則化后 → 參數值:[2, 1.5, -1.2](數值變小,模型更平緩)
2. L1 正則化:讓參數 “消失”
- 效果:直接讓不重要的參數變成 0(相當于刪掉這些參數),實現 “特征選擇”,讓模型更 “簡潔”。
- 圖示:
無正則化 → 參數值:[10, 8, -7](3個參數都在用) L1正則化后 → 參數值:[3, 0, -2](中間參數被“刪掉”,只剩2個有用參數)
3、正則化的強度控制(λ 的作用)
正則化的 “懲罰力度” 由參數 λ 控制:
λ太小 → 懲罰太輕 → 模型還是復雜(可能過擬合)
λ適中 → 懲罰剛好 → 模型簡單且準確(最佳狀態)
λ太大 → 懲罰太重 → 模型太簡單(連基本規律都沒學到,欠擬合)
圖示
模型效果(測試集 accuracy)
↑
| 最佳λ → 效果峰值
| ┌───┐
| / \
| / \
| / \
+------------→ λ(懲罰力度) 過擬合 欠擬合 (λ小) (λ大)
正則化的核心就是:給復雜模型 “加約束”,通過懲罰大參數或冗余參數,讓模型在 “擬合數據” 和 “保持通用” 之間找平衡。
- L2 正則化:讓參數變 “小”,模型更穩健;
- L1 正則化:讓參數變 “少”,模型更簡潔;
- 選對懲罰力度(λ),模型才能既不 “學太死”,也不 “學不會”。
三、交叉驗證
交叉驗證是機器學習中評估模型 “真實能力” 的常用方法,能幫我們避免因數據劃分不合理導致的評估偏差,判斷模型是否真正 “學好了”。以下用通俗語言和圖示介紹。
1、為什么需要交叉驗證?—— 避免 “運氣成分”
假設你訓練模型時,隨機把數據分成 “訓練集”(學知識)和 “測試集”(考考試):
- 如果測試集剛好很簡單,模型分數會虛高;
- 如果測試集剛好很難,模型分數會偏低。
問題:一次劃分的結果可能受 “運氣” 影響,無法反映模型真實水平。
交叉驗證的作用:通過多次劃分數據、多次評估,取平均值,讓結果更可靠,就像 “多次考試取平均分” 更能反映真實成績。
2、最常用的交叉驗證:K 折交叉驗證(圖示步驟)
以 “5 折交叉驗證” 為例,步驟如下:
1. 數據劃分
把所有數據均勻分成?K 份(比如 5 份,每份叫一個 “折”):
原始數據 → [折1] [折2] [折3] [折4] [折5] (每份數據量相近)
2. 多次訓練與評估
每次用?K-1 份當訓練集,剩下 1 份當測試集,重復 K 次(每個折都當一次測試集):
第1次:訓練集=[折2,3,4,5] → 測試集=[折1] → 得分數1
第2次:訓練集=[折1,3,4,5] → 測試集=[折2] → 得分數2
第3次:訓練集=[折1,2,4,5] → 測試集=[折3] → 得分數3
第4次:訓練集=[折1,2,3,5] → 測試集=[折4] → 得分數4
第5次:訓練集=[折1,2,3,4] → 測試集=[折5] → 得分數5
3. 結果平均
把 K 次的分數取平均值,作為模型的最終評估結果:
最終分數 = (分數1 + 分數2 + 分數3 + 分數4 + 分數5)÷ 5
2、交叉驗證的優勢(對比單次劃分)
| 方法 | 優點 | 缺點 |
|---|---|---|
| 單次劃分( train/test ) | 簡單快速 | 結果受隨機劃分影響大,數據利用率低 |
| K 折交叉驗證 | 結果更穩定可靠,充分利用所有數據 | 計算量增加(需訓練 K 次模型) |
4、其他常見交叉驗證類型
1. 留一交叉驗證(Leave-One-Out)
- 把數據分成 N 份(N 等于樣本數量),每次留 1 個樣本當測試集,重復 N 次。
- 優點:結果極可靠;缺點:計算量極大(適合小數據集)。
2. 分層 K 折交叉驗證
- 當數據不平衡(比如 90% 是正例,10% 是負例),保證每個折中正負例比例和原始數據一致。
- 例:原始數據正:負 = 9:1 → 每個折中也保持 9:1,避免測試集全是正例的極端情況。
5、交叉驗證的核心作用
- 評估模型泛化能力:判斷模型是否能在新數據上表現良好,而非只 “死記” 訓練數據。
- 選擇最佳參數:比如用交叉驗證比較不同 λ 的正則化效果,選分數最高的 λ。
- 減少數據浪費:充分利用有限數據,尤其適合小數據集。
四、下采樣和過采樣
在機器學習中,采樣是處理類別不平衡問題(即數據集中某一類樣本數量遠多于另一類)的常用方法。過采樣和下采樣是兩種主要策略,核心目標是通過調整樣本比例,讓模型更公平地學習不同類別的特征。
1. 下采樣(Undersampling)
- 核心思想:減少多數類(樣本多的類別)的數量,使其與少數類(樣本少的類別)數量接近。
- 操作方式:從多數類樣本中隨機挑選一部分,丟棄其余樣本,讓兩類樣本數量大致平衡。
- 例子:
假設數據集中有 1000 個正常交易(多數類)和 10 個欺詐交易(少數類),下采樣可能會從 1000 個正常交易中隨機選 10 個,最終用 10 個正常 + 10 個欺詐樣本訓練模型。 - 優點:計算成本低(樣本量變少)。
- 缺點:可能丟失多數類中的重要信息(被丟棄的樣本可能包含關鍵特征)。
2. 過采樣(Oversampling)
- 核心思想:增加少數類(樣本少的類別)的數量,使其與多數類數量接近。
- 操作方式:通過復制少數類樣本,或用算法生成 “新的少數類樣本”(如 SMOTE 算法:基于現有少數類樣本的特征,生成相似的虛擬樣本),擴大少數類規模。
- 例子:
對上述 10 個欺詐交易,過采樣可能會復制它們 100 次(或生成 990 個相似樣本),最終用 1000 個正常 + 1000 個欺詐樣本訓練模型。 - 優點:保留多數類的全部信息,避免關鍵數據丟失。
- 缺點:簡單復制可能導致模型過擬合少數類(記住重復樣本的細節);生成虛擬樣本需謹慎,避免引入噪聲。
總結對比
| 方法 | 核心操作 | 適用場景 | 關鍵問題 |
|---|---|---|---|
| 下采樣 | 減少多數類樣本 | 多數類樣本極多、計算資源有限 | 可能丟失重要信息 |
| 過采樣 | 增加少數類樣本(復制 / 生成) | 少數類樣本有價值但數量少 | 可能過擬合、需合理生成樣本 |
實際應用中,常結合兩者(如 “過采樣少數類 + 下采樣多數類”)或配合其他策略(如調整模型權重)來處理不平衡問題。
五、銀行借貸案例
假設有一個銀行,統計了很多貸款人的多條數據和對應的還款情況,想讓你分析建立一個模型來檢驗一個即將貸款的人是否會按規定還款
數據集的大致形狀如圖所示(數據集可以去我主頁下載)
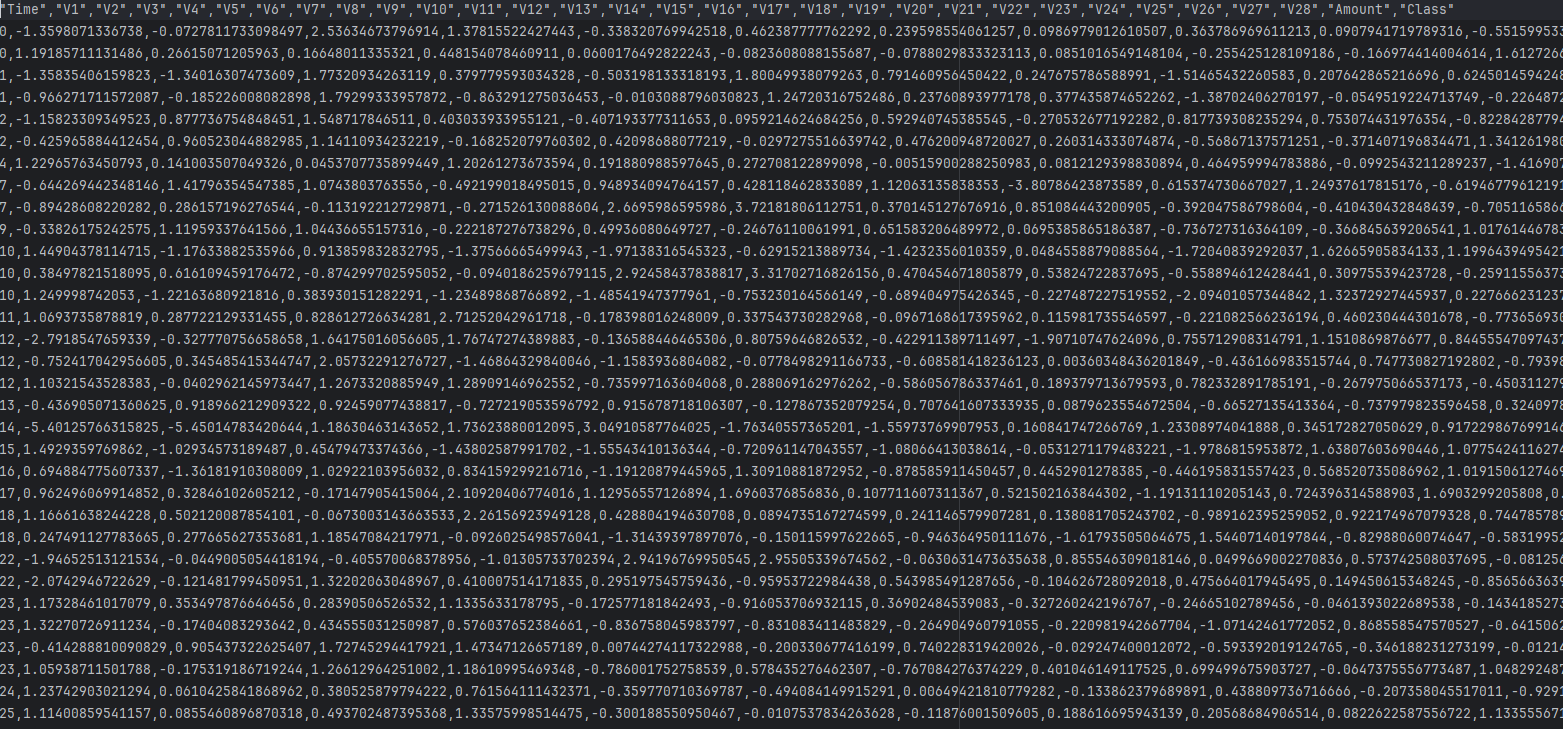
進過前幾天的學習,你很高興的寫出來如下代碼
# 導入必要的庫
import pandas as pd # 用于數據處理和分析
from sklearn.preprocessing import StandardScaler # 用于數據標準化
from sklearn.linear_model import LogisticRegression # 導入邏輯回歸模型
from sklearn.model_selection import train_test_split # 用于拆分訓練集和測試集
from sklearn import metrics # 用于模型評估指標計算# 讀取信用卡交易數據
# 數據集包含信用卡交易信息,其中'Class'列為目標變量(1表示欺詐交易,0表示正常交易)
date = pd.read_csv('creditcard.csv')# 初始化標準化器,將數據縮放到均值為0、標準差為1的范圍
sal = StandardScaler()
# 對交易金額(Amount)進行標準化處理,使其與其他特征具有相同的量級
date['Amount'] = sal.fit_transform(date[['Amount']])# 刪除'Time'列(時間特征),因為該特征對欺詐檢測可能沒有幫助
date = date.drop(['Time'], axis=1)# 劃分特征變量(X)和目標變量(y)
# 取除最后一列之外的所有列作為特征
x = date.iloc[:, :-1]
# 取最后一列'Class'作為目標變量(是否為欺詐交易)
y = date['Class']# 將數據集拆分為訓練集和測試集
# test_size=0.3表示30%的數據作為測試集,70%作為訓練集
# random_state=42保證每次運行代碼時拆分結果一致,便于復現
xtr, xte, ytr, yte = train_test_split(x, y, test_size=0.3, random_state=42)# 初始化邏輯回歸模型
# C=0.01:正則化強度的倒數,值越小正則化越強
# penalty='l2':使用L2正則化(嶺回歸)
# solver='lbfgs':優化算法
# max_iter=1000:最大迭代次數,確保模型收斂
lr = LogisticRegression(C=0.01, penalty='l2', solver='lbfgs', max_iter=1000)# 訓練模型(注意:這里使用了全部數據訓練,而不是之前拆分的訓練集xtr)
lr.fit(x, y)# 使用訓練好的模型對測試集進行預測
test_predicted = lr.predict(xte)# 計算模型在測試集上的準確率
score = lr.score(xte, yte)# 輸出預測結果
print("預測結果:", test_predicted)
# 輸出模型準確率
print("模型準確率:", score)
# 輸出詳細的分類評估報告,包括精確率、召回率、F1分數等
# 對于欺詐檢測這類不平衡數據,這些指標比單純的準確率更有參考價值
print(metrics.classification_report(yte, test_predicted))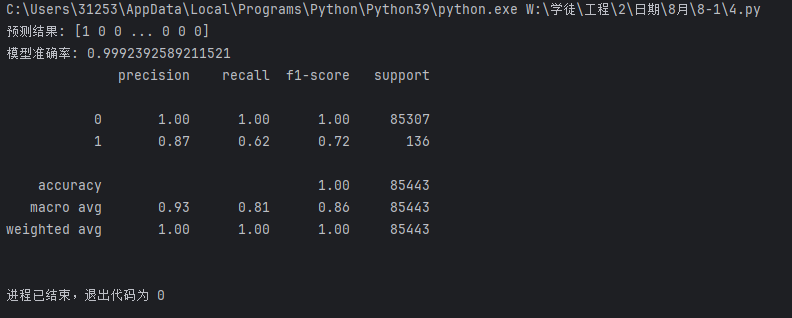
看了一下結果,不錯,99.92%的模型準確率,你很高興,但是銀行的甲方斜著眼看你要你出門右轉,為啥呢?
因為1這個數據的召回率(Recall)只有62%,和瞎猜的50%差不多,這個肯定不達標
這時你想了想,嘗試換了參數,但怎么換呢?
可以試試用交叉驗證來求出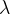 的最佳值
的最佳值
于是寫出以下代碼
import pandas as pd
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn import metrics
import numpy as np
date = pd.read_csv('creditcard.csv')
sal = StandardScaler()
date['Amount'] = sal.fit_transform(date[['Amount']])
date = date.drop(['Time'],axis = 1)
x = date.iloc[:,:-1]
y = date['Class']
xtr,xte,ytr,yte=train_test_split(x,y,test_size=0.3,random_state=42)
######################################
from sklearn.model_selection import cross_val_score
scores = []
c_param_range = [0.01,0.1,1,10,100]
for i in c_param_range:lr = LogisticRegression(C=i,penalty='l2',solver='lbfgs',max_iter=1000)score = cross_val_score(lr,xtr,ytr,cv=10,scoring='recall')score_mean = sum(score)/len(score)scores.append(score_mean)print(score_mean)
best_c = c_param_range[np.argmax(scores)]
print('最佳的懲罰值:',best_c)
##################################
lr = LogisticRegression(C=best_c,penalty='l2',solver='lbfgs',max_iter=1000)
lr.fit(x,y)
test_predicted = lr.predict(xte)
score = lr.score(xte,yte)
print("預測結果:", test_predicted)
print("模型準確率:", score)
print(metrics.classification_report(yte,test_predicted))
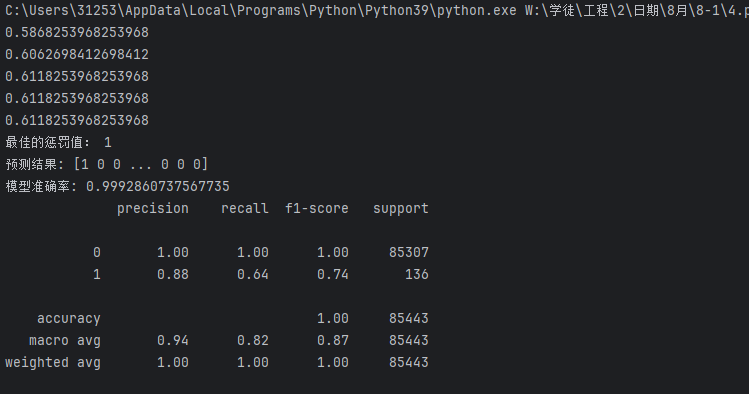
發現有改變,但不大
繼續找方法
這時發現訓練數據里面0的數據有幾十萬,但1的數據只有幾百條
突然,你想到了下采樣和過采樣的方法,于是寫出下列兩個代碼
下采樣:
import pandas as pd
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn import metrics
import numpy as np
date = pd.read_csv('creditcard.csv')
sal = StandardScaler()
date['Amount'] = sal.fit_transform(date[['Amount']])
date = date.drop(['Time'],axis = 1)
x = date.iloc[:,:-1]
y = date['Class']
xtr,xte,ytr,yte=train_test_split(x,y,test_size=0.3,random_state=42)
##################################
new_date = xtr.copy()
new_date['Class'] = ytr
positive_eg = new_date[new_date['Class']==0]
negative_eg = new_date[new_date['Class']==1]
positive_eg = positive_eg.sample(len(negative_eg))
date_c = pd.concat([positive_eg,negative_eg])
x = date_c.iloc[:,:-1]
y = date_c['Class']
##################################
from sklearn.model_selection import cross_val_score
scores = []
c_param_range = [0.01,0.1,1,10,100]
for i in c_param_range:lr = LogisticRegression(C=i,penalty='l2',solver='lbfgs',max_iter=1000)score = cross_val_score(lr,xtr,ytr,cv=10,scoring='recall')score_mean = sum(score)/len(score)scores.append(score_mean)print(score_mean)
best_c = c_param_range[np.argmax(scores)]
print('最佳的懲罰值:',best_c)
lr = LogisticRegression(C=best_c,penalty='l2',solver='lbfgs',max_iter=1000)
lr.fit(x,y)
test_predicted = lr.predict(xte)
score = lr.score(xte,yte)
print("預測結果:", test_predicted)
print("模型準確率:", score)
print(metrics.classification_report(yte,test_predicted))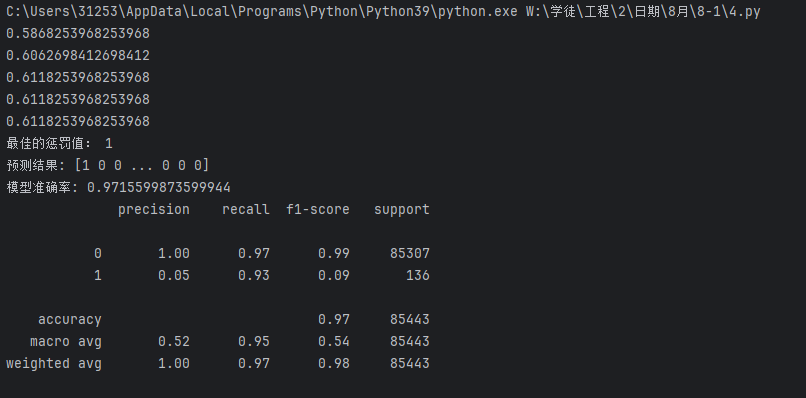
過采樣:
import pandas as pd
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn import metrics
import numpy as np
print('過采樣')
date = pd.read_csv('creditcard.csv')
sal = StandardScaler()
date['Amount'] = sal.fit_transform(date[['Amount']])
date = date.drop(['Time'],axis = 1)
x = date.iloc[:,:-1]
y = date['Class']
xtr,xte,ytr,yte=train_test_split(x,y,test_size=0.3,random_state=42)
############################################
from imblearn.over_sampling import SMOTE
oversampler = SMOTE(random_state=1000)
os_xtr,os_ytr = oversampler.fit_resample(xtr,ytr)
x = os_xtr
y = os_ytr
##########################################
from sklearn.model_selection import cross_val_score
scores = []
c_param_range = [0.01,0.1,1,10,100]
for i in c_param_range:lr = LogisticRegression(C=i,penalty='l2',solver='lbfgs',max_iter=1000)score = cross_val_score(lr,xtr,ytr,cv=10,scoring='recall')score_mean = sum(score)/len(score)scores.append(score_mean)print(score_mean)
best_c = c_param_range[np.argmax(scores)]
print('最佳的懲罰值:',best_c)
lr = LogisticRegression(C=best_c,penalty='l2',solver='lbfgs',max_iter=1000)
lr.fit(x,y)
test_predicted = lr.predict(xte)
score = lr.score(xte,yte)
print("預測結果:", test_predicted)
print("模型準確率:", score)
print(metrics.classification_report(yte,test_predicted))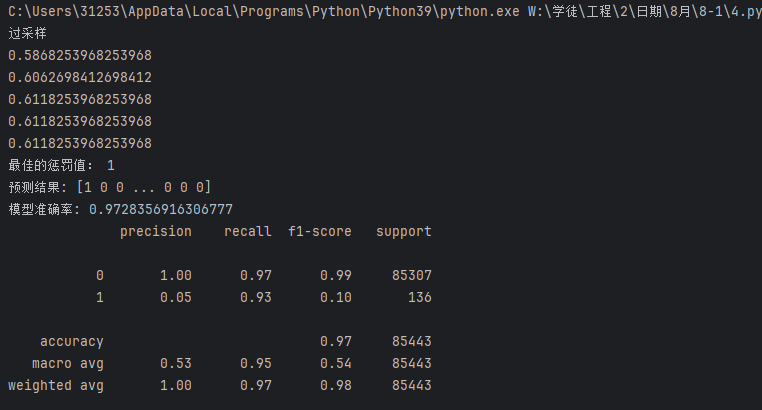
運行完你很高興,準確率提高了不少
數據1的精確率(Precision)不太重要,畢竟銀行錯了沒有損失,但漏了一個的損失就不小了
對比一下發現效果差不多,
但是甲方說要達到95%才行
于是你拿出另一個辦法--改闕值
分類閾值的作用:邏輯回歸默認使用 0.5 作為閾值(正類概率 > 0.5 則判定為正類),但在欺詐檢測等場景中,我們可能需要調整閾值以提高對少數類(欺詐交易)的識別能力。
為何關注召回率:在檢測中,召回率(對真實欺詐交易的識別率)通常比準確率更重要,因為漏檢(假負例)的代價可能遠高于誤判(假正例)。
閾值調整的影響:
- 降低閾值(如 0.1):模型更 “容易” 判定為正類,可能提高召回率(減少漏檢),但可能增加假正例
- 提高閾值(如 0.9):模型更 “嚴格” 判定為正類,可能降低召回率(增加漏檢),但假正例會減少
這里用便利循環的方法來修改(在代碼 最后加上以下代碼)
# 定義一系列分類閾值(決策閾值),范圍從0.1到0.9
# 分類閾值是模型判斷樣本屬于正類的概率臨界點
thresholds = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9]
# 用于存儲不同閾值對應的召回率
recalls = []
# 遍歷每個閾值,計算并觀察召回率變化
for i in thresholds:# 獲取模型對測試集的預測概率# 返回值是一個二維數組,每行包含兩個概率:[負類概率, 正類概率]y_predict_proba = lr.predict_proba(xte)# 將概率數組轉換為DataFrame,方便處理y_predict_proba = pd.DataFrame(y_predict_proba)# 根據當前閾值i調整預測結果:# 當正類(索引1對應的類別,即欺詐交易)的概率大于i時,判定為正類(1)y_predict_proba[y_predict_proba[[1]] > i] = 1# 當正類概率小于等于i時,判定為負類(0)y_predict_proba[y_predict_proba[[1]] <= i] = 0# 計算當前閾值下的召回率(Recall)# 召回率 = 真正例/(真正例+假負例),衡量模型對正類(欺詐交易)的識別能力recall = metrics.recall_score(yte, y_predict_proba[1])# 將當前閾值的召回率存入列表recalls.append(recall)# 打印當前閾值和對應的召回率,觀察變化趨勢print(i, recall)
print(f'調整閾值后的recall為:{max(recalls)}')
#這里直接輸出1這個數據的召回率(Recall)運行結果:
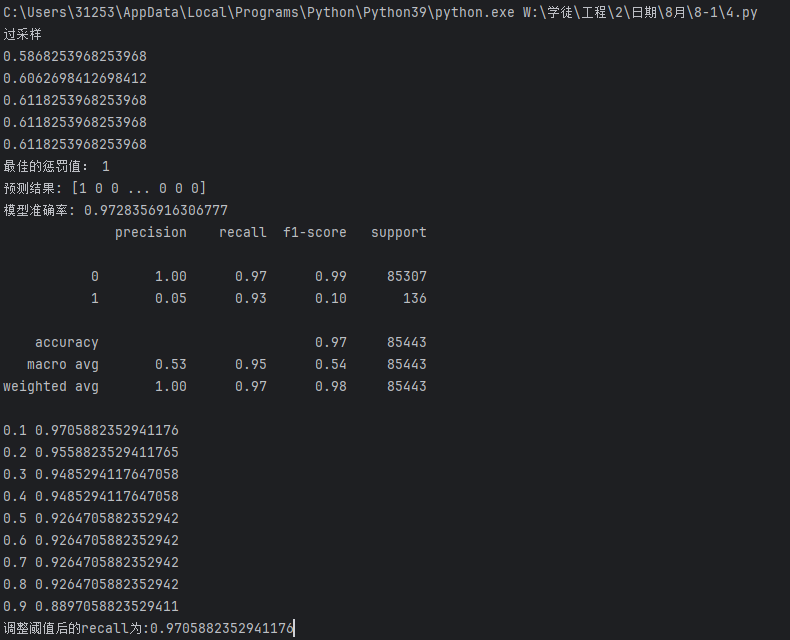
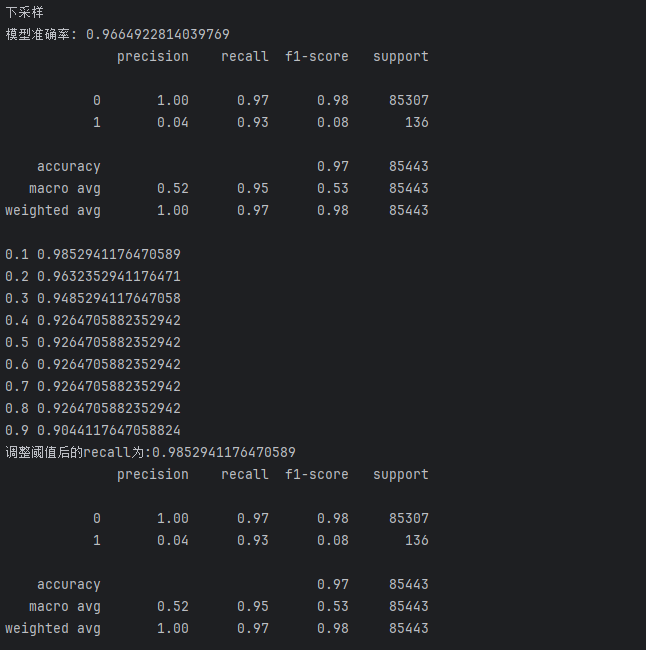
發現下采樣效果好一點
但實際上也可以通過分割訓練集測試集的隨機種子來調整準確率的高低,但這個太費時間還沒有定數,這里就不管了
最后,你把模型交給了銀行的甲方
任務大功告

)
)





)










