---

前言

紅黑樹是比較重要的一顆樹了，map和set的底層就是紅黑樹，一定要牢牢記住。

---

一、什么是紅黑樹

首先：紅黑樹仍然是一顆搜索二叉樹，但他引入了顏色這一概念，每個結點多一個存儲位來存儲顏色，它通過維護下面五條規則來保證，最長路徑不超過最短路徑的二倍。

1.每個結點不是黑顏色就是紅顏色
2.根節點是黑色
3.如果一個節點是紅色，則他存在的孩子節點是黑色，換句話說，任意一條路徑不存在連續的紅色節點。
4.對于每個節點，到所有NIL節點的路徑上，均含有相同數量的黑色節點。
5.每個NIL節點都是黑色的
為什么設計第五條規則？看圖：

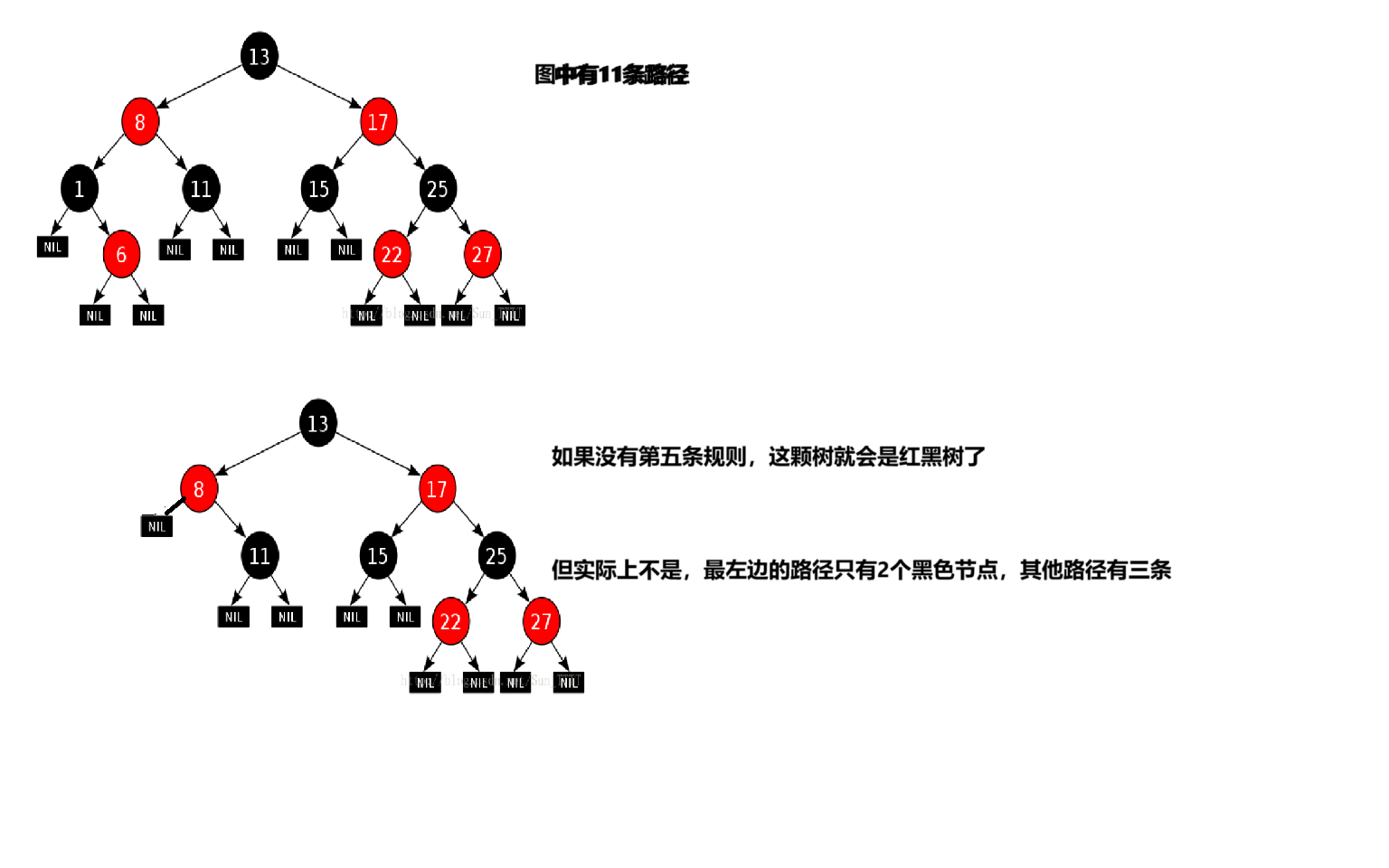
這五條規則里最重要的就是三和四，插入也要維護三和四。

為什么維護了這五條規則就能達到最長路徑不超過最短路徑的二倍呢？
最短路徑：全是黑色節點
最長路徑：一黑一紅，又因為黑色節點的數量相同，所以最長的路徑最多是最短路徑的二倍。

二、模擬

紅黑樹還是模擬插入過程，還是寫成K，V和三叉鏈結構

節點定義

enum class Color {RED,BLACK
};template<class K,class V>
struct RBTreeNode {RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Color color;pair<K, V> _kv;RBTreeNode(const pair<K,V>& p):_left(nullptr),_right(nullptr),_parent(nullptr),color(Color::RED),_kv(p){}
};

這里有兩個注意的點：
1.這個枚舉是C++新搞出來的，和原來枚舉不同的就是不是全局的。
2.節點的默認顏色搞成紅色，如果搞成黑色，這一條路徑上的黑色節點加一，而其他所有路徑上的黑色數目就會相對較少，不好維護，所以違反第三條規則，維護第三條規則，這需要維護這一條和叔叔路徑上的。

搜索樹的邏輯插入：

bool insert(const pair<K, V>& p)
{if (_root == nullptr){_root = new Node(p);_root->color = Color::BLACK;return true;}else{Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first < p.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > p.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(p);if (parent->_kv.first < p.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//這之前都是搜索樹的邏輯//

調整顏色的邏輯：

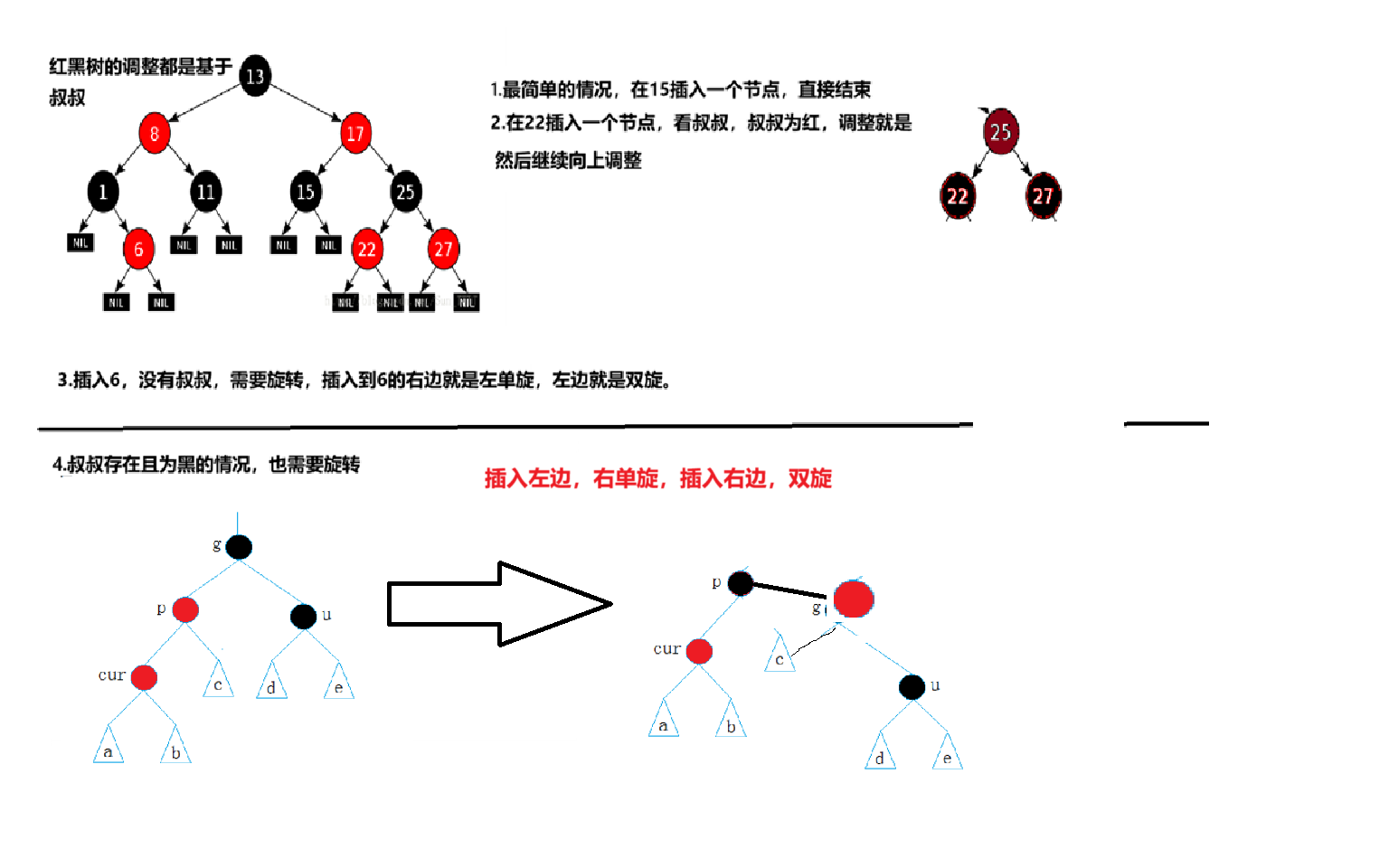
	while (parent && parent->color == Color::RED){Node* grandf = parent->_parent;if (grandf->_left == parent){Node* uncle = grandf->_right;//叔叔存在且為紅if (uncle && uncle->color == Color::RED){//判斷uncle->color = parent->color = Color::BLACK;grandf->color = Color::RED;//繼續判斷cur = grandf;parent = cur->_parent;}//叔叔不存在或者為黑else{//開旋if (parent->_left == cur){RotateRight(grandf);parent->color = Color::BLACK;grandf->color = Color::RED;}else{//parent->right  是cur，grandf的左邊是parentRotateLeft(parent);RotateRight(grandf);cur->color = Color::BLACK;grandf->color = Color::RED;}}}//祖父的右邊是父親else{Node* uncle = grandf->_left;//uncle不存在 或者uncle為黑//uncle為紅if (uncle && uncle->color == Color::RED){parent->color = uncle->color = Color::BLACK;grandf->color = Color::RED;cur = grandf;parent = cur->_parent;}//uncle為黑或者不存在else{//旋轉//   grandf//uncle                parent//curif (cur == parent->_right){RotateLeft(grandf);parent->color = Color::BLACK;grandf->color = Color::RED;}else{RotateRight(parent);RotateLeft(grandf);cur->color = Color::BLACK;grandf->color = Color::RED;}}}}_root->color = Color::BLACK;return true;
}

其實還可以，順一順思路：
當父親存在并且父親的顏色是紅就更新
先判斷祖父的左邊是父親還是右邊，需要根據這個旋轉
然后判斷uncle，也就是祖父的另一個孩子，如果uncle為紅，和parent一起改顏色，往上更新。
如果為黑或者不存在，要旋轉，直線型單旋，折線型雙旋，注意控制顏色，旋轉完的父親一定為黑，左右兩個孩子都為紅。

三、驗證是否正確

1.驗證是否為二叉搜索樹，走一個中序遍歷就可以,有序即為二叉搜索樹。

2.驗證是否紅黑樹滿足條件：
主要是看三和四，三：看有無連續紅色節點，利用父親來判斷，
四：看黑色節點的數量，可以先求出一條路徑的數量，然后再去遞歸所有路徑進行比較。

bool CheckColor(Node* node,int blacknum,int basic)
{
if (node == nullptr)
{if (blacknum != basic){cout << "違背了第四條規則" << endl;return false;}return true;
}
if (node->color == Color::BLACK)
{blacknum++;
}
//檢查孩子很麻煩，檢查父親
if (node->color == Color::RED && node->_parent && node->_parent->color == Color::RED)
{cout << "出現了連續的紅色結點" << endl;return false;
}
return CheckColor(node->_left,blacknum,basic) && CheckColor(node->_right, blacknum, basic);}
bool _IsBalance(Node* node)
{if (node == nullptr) return true;if (node->color != Color::BLACK){//根節點是黑色return false;//第二條}int basic = 0;Node* cur = node;while (cur){if (cur->color == Color::BLACK){basic++;}cur = cur->_left;}return CheckColor(node,0,basic);
}

四、性能

代碼測試

int main()
{RBTree<int, int> rb;AVLTree<int, int> avl;srand(time(0));size_t N = 100000000;vector<int> v(N);for (size_t i = 0; i < N; ++i) v[i] = rand() + i;int begin1 = clock();for (size_t i = 0; i < N; ++i) {rb.insert({ v[i],v[i] });}int end1 = clock();int begin2 = clock();for (size_t i = 0; i < N; ++i){avl.insert({ v[i],v[i] });}int end2 = clock();if (rb.IsBalance() && avl.IsBalance()){cout << "插入" << N << "個數據" << "紅黑樹用時間" << end1 - begin1 << ' ' << "旋轉次數:" << rb.RotateCount;cout << endl;cout << "插入" << N << "個數據" << "AVL樹用時間" << end2 - begin2 << ' ' << "旋轉次數:" << avl.Rotatecount;}return 0;
}

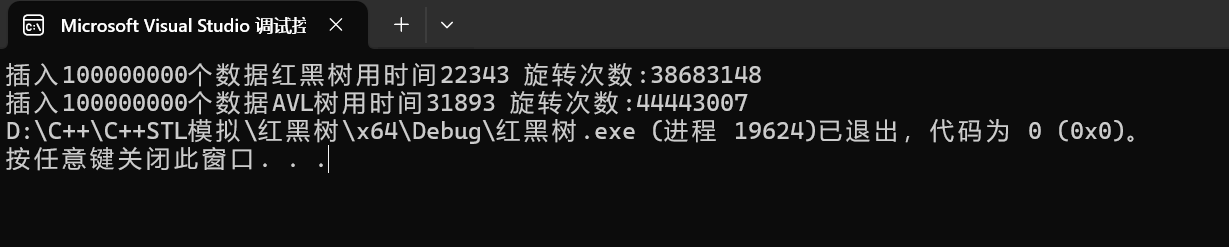
還可以去測試一下他們的高度，有序數據，隨機數據，查找的效率等等。
總體來說，紅黑樹是更優秀的，數據量越大紅黑樹的優勢就越明顯。

紅黑樹和AVL樹都是高效的平衡二叉樹，增刪改查的時間復雜度都是O(logN)，紅黑樹不追求絕對平衡，其只需保證最長路徑不超過最短路徑的2倍，相對而言，降低了插入和旋轉的次數，所以在經常進行增刪的結構中性能比AVL樹更優，而且紅黑樹實現比較簡單，所以實際運用中紅黑樹更多。

---

五、完整代碼

個人gitee

總結

紅黑樹很重要！！！！一定要牢牢掌握。
接下來map和set還需要使用它。