排序復習/上（C語言版）

1.排序概念

2.冒泡排序

效率性能測試代碼：

?性能分析：

3.直接插入排序

單趟：

整體：

性能分析：

4.希爾排序（基于插入排序的優化）

單趟單組：

?單趟多組：

降低循環層次的辦法：

整體：

性能分析：

5.選擇排序

6.堆排序

1.排序概念

讓所有數據從小到大/從大到小，就是排序的概念

常見的排序算法：

1.直接插入排序 2.希爾排序

3.選擇排序 4.堆排序

5.冒泡排序 6.快速排序

7.歸并排序

2.冒泡排序

效率性能測試代碼：


void TestOP()
{srand(time(0));const int N = 50000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);int* a7 = (int*)malloc(sizeof(int) * N);int* a8 = (int*)malloc(sizeof(int) * N);int* a9 = (int*)malloc(sizeof(int) * N);int* a10 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){//重復數據多（函數特性，隨機值范圍在0~32767）a1[i] = rand();//重復數據不多//a1[i] = rand() + i;a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];a8[i] = a1[i];a9[i] = a1[i];a10[i] = a1[i];}int begin1 = clock();InsertSort(a1, N);int end1 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();int begin3 = clock();SelectSort(a3, N);int end3 = clock();int begin4 = clock();HPSort(a4, N);int end4 = clock();int begin5 = clock();QuickSort(a5, 0, N - 1);int end5 = clock();int begin6 = clock();MergeSort(a6, N);int end6 = clock();int begin7 = clock();BubbleSort(a7, N);int end7 = clock();int begin8 = clock();QuickSortNON(a8, 0, N - 1);int end8 = clock();int begin9 = clock();MergeSortNON(a9, N);int end9 = clock();int begin10 = clock();CountSort(a10, N);int end10 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("ShellSort:%d\n", end2 - begin2);printf("SelectSort:%d\n", end3 - begin3);printf("HeapSort:%d\n", end4 - begin4);printf("QuickSort:%d\n", end5 - begin5);printf("QuickSortNON:%d\n", end8 - begin8);printf("MergeSort:%d\n", end6 - begin6);printf("MergeSortNON:%d\n", end9 - begin9);printf("BubbleSort:%d\n", end7 - begin7);printf("CountSort:%d\n", end10 - begin10);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);free(a7);free(a8);free(a9);free(a10);
}int main()
{TestOP();return 0;
}

rand()范圍在0~32767，如果有32769個數據那么就肯定有至少一個數據是重復的

為了降低重復數量，因此可以+i 來優化??

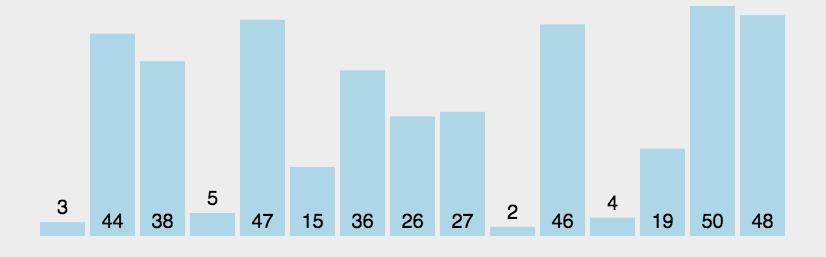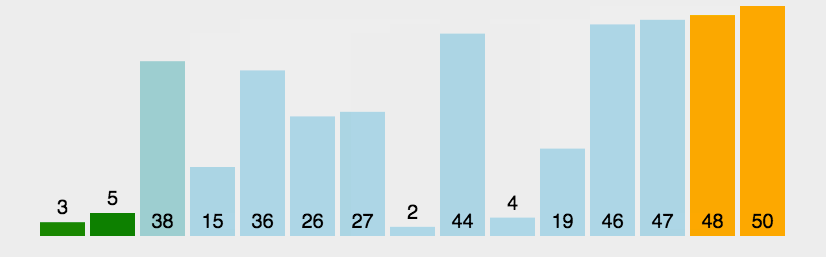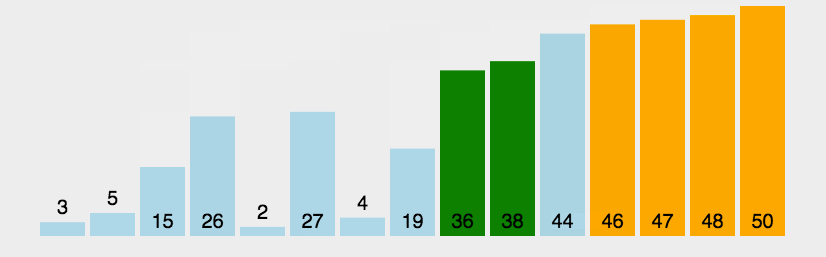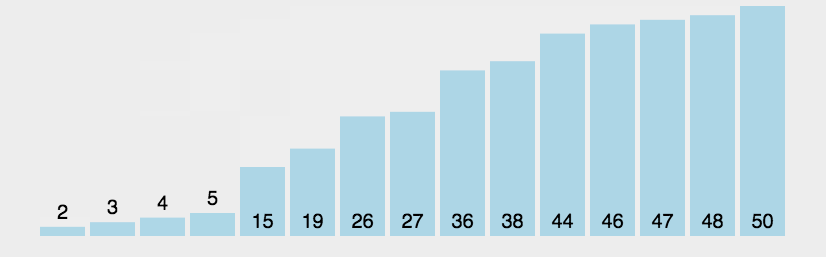
	for (int j = 0;j < n;j++){//單趟for (int i = 0;i < n - j - 1;i++){if (a[i] > a[i + 1]) Swap(&a[i], &a[i + 1]);}}

冒泡排序：前后比較往后交換，交換時可以把大的往后挪，因此每次交換完可以把一個位置的元素確定好位置

最開始的一次要冒泡到n-1位置，為防止越界需要考慮清楚循環推出條件；當 j = 0 時，n - 1 = i 的話會出現a[n]越界，因此循環退出條件還需要 - 1

優化：若[0,j]位置沒有發生任何交換，說明已經有序了，直接停止循環

void BubbleSort(int* a, int n)
{for (int j = 0;j < n;j++){//單趟int flag = 1;for (int i = 0;i < n - j - 1;i++){if (a[i] > a[i + 1]) Swap(&a[i], &a[i + 1]);flag = 0;}if (flag) break;}}

?性能分析：

?時間復雜度：
?最壞：N^2
?最好：N,數據已經有序

3.直接插入排序

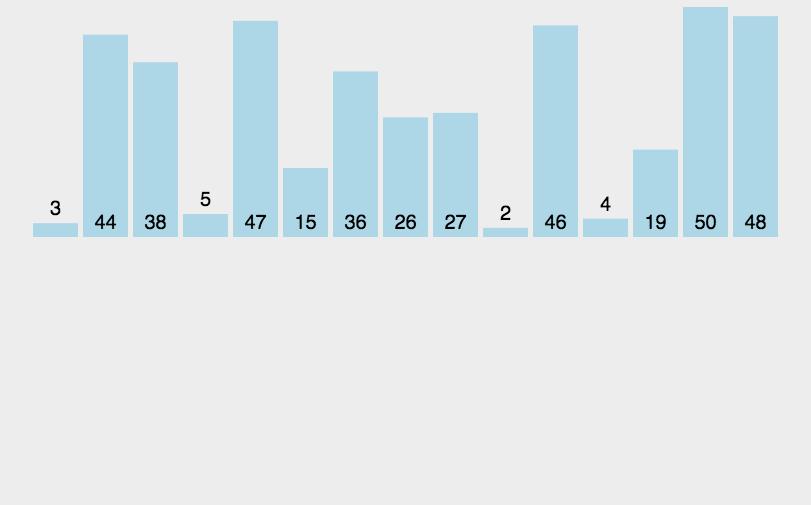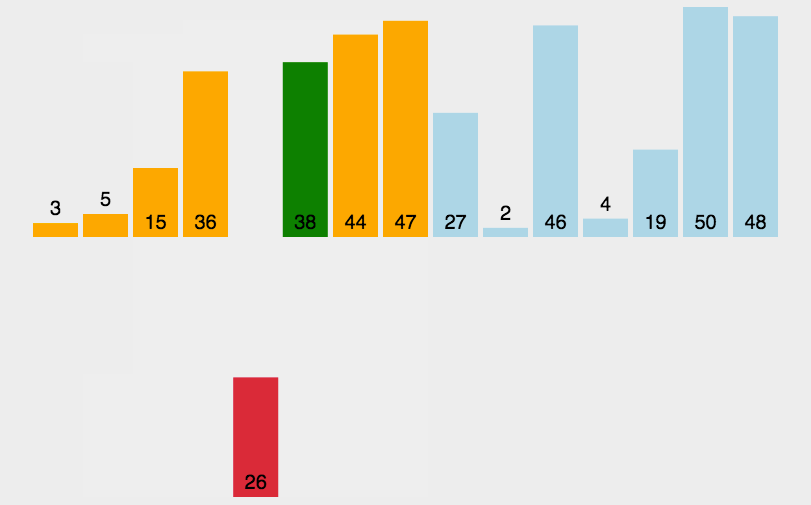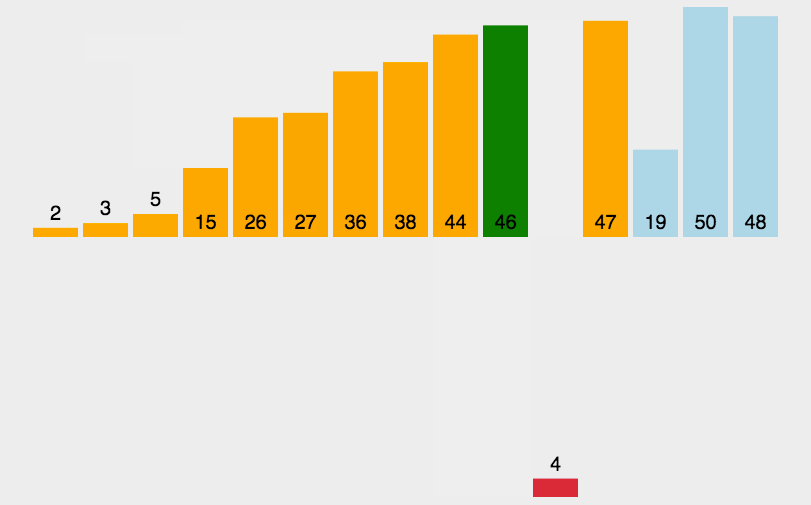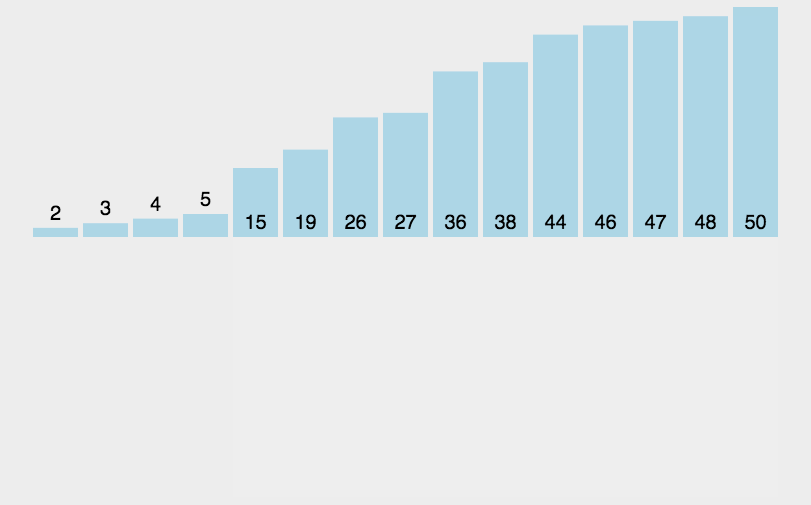
概念：對一個數組[3,9,10,21,5,4]，假設要升序排序；5往前移動，先和10、21比較，無法插入；再往前移動，和9、10比較，無法插入；再往前移動，和3、9比較，可以插入（斗地主整理手牌用到的就是插入排序的思想）

排序思想：以上圖為例，先把end下標后面一個元素（假設為tmp）保存下來，然后依次比較end下標元素和tmp大小，如果不合適就把從end往后覆蓋1位，直到tmp到了合適的位置，把保存下來的值覆蓋原來end+1下標元素（這樣end+1下標元素才不會在數組中重復兩次）

整體邏輯：[0,end]排序完畢，[end+1,size] 需要排序，因此直接直接在數組中從頭到尾對每個下標元素往前做一次插入排序，即能完成排序

極端情況：當tmp是整個數組最小的，此時end下標會變成-1，需要解決

在處理復雜函數時，我們可以先從單趟排序寫起，然后拓展到整體排序

單趟：

	int end;int temp = a[end + 1];while (end >= 0){if (temp < a[end]){a[end + 1] = a[end]; end--;}else break; }a[end + 1] = temp;

??? 假設[0,end]有序，end+1位置的值往前比較插入
?? ?為防止覆蓋后，原值不在，因此需要有一個temp存儲end+1位置的值

? ? "a[end + 1] = a[end];" 要想把數據往后挪，通過覆蓋后一個值的方法

? ? 當temp比end下標值大，則比[0,end]位置的值都大；可以直接覆蓋掉此時end+1下標位置的元素（因為已經將原來temp位置的元素已經覆蓋掉了，[end+1,end+2]位置的元素相同了）

整體：

void InsertSort(int* a, int n)
{for (int i = 0;i < n - 1;i++){int end = i;int temp = a[end + 1];while (end >= 0){if (temp < a[end]){a[end + 1] = a[end]; end--;}else break; }a[end + 1] = temp;}
}

對每個數進行一次插入排序，從[0,end]有序到[0,n]有序
只能遍歷到n-2，temp = a[n] 會導致數組越界

通過循環語句的推出條件，直接解決了極限情況；出現極限情況時end為-1，a[end+1] = a[0] = temp

性能分析：

?? ?時間復雜度：
?? ? 最壞：N^2，逆序時是最壞情況（一次break語句都不會執行）
?? ? 最好：N，順序時是最好情況（每個temp進入循環就break）

?? ?為什么與冒泡排序時間復雜度相同，但實際運行起來插入排序快那么多？
?? ?首先，我們剛剛考慮的只是最好、最壞的情況，沒有考慮普遍情況
?? ?對于插入排序，只要temp比[0,end]位置中的某一數據大時，就可以直接break；每一個數據往前排的時候大概率都能進行break，或多或少跳過了幾個數據沒有運行，積少成多，運行時間就大大縮減了
?? ?對于冒泡排序，只有[0,j]位置完全有序才能break，break的條件比較苛刻；同時，只有完全有序時才能停止循環，無法像插入排序那樣積少成多

4.希爾排序（基于插入排序的優化）

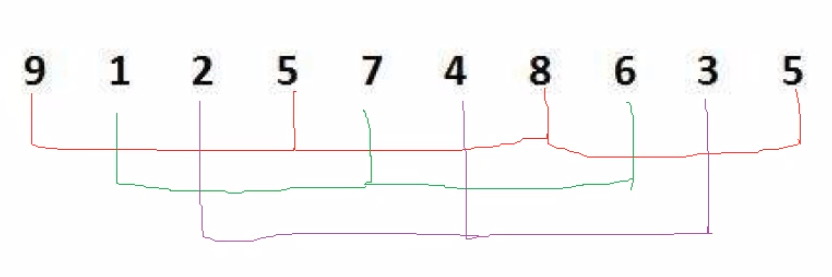
?? ?希爾排序：
?? ?1.預排序（讓數據接近有序）
?? ?2.對已經預排序完的數組進行插入排序
?? ?插入排序的不足之處：每個數都有概率往前移動非常多次才能break；希爾排序就是基于插入排序優化，用來解決插入排序的這一不足

? ? 1.單組預排序
?? ?預排序的方法：將n個數分為gap組，兩數間隔為gap的為一組（如上圖），然后對每一組分別進行插入排序；此時假設有一個大的數在數組最后位置，(升序排序時）往前跳得比較快，能一次跳gap個數
?? ?把插入排序的 1 全部改成 gap 即可，因為是對兩數相隔為gap的組進行插入排序（從相隔為1 -> 相隔為gap）

?? ?2.多組預排序
?? ?總共有分別以[0,gap-1]下標為開頭元素的gap組，因此外面套一層[0,gap-1]的循環

?? ?3.整體排序：
?? ?gap == 1 時，相當于插入排序了；gap > 1 時，相當于預排序
?? ?因此我們可以使用這樣的一個思想：用預排序組成整體排序
?? ?gap越大，每組中的元素跳得越快，數組越無序；gap越小，每組中的元素跳得越慢，數組越有序
?? ?gap怎么變化最好？科學研究每次 gap/3 是最好的
?? ?gap = gap/3 ，假設gap為2時,最后結果為0，gap為0就不會對數組元素進行排序，因此需要在末尾 +1 來保證最小的gap值為1

單趟單組：

	int gap = 3;//假設gap為3for (int i = 0;i < n - gap;i += gap) //為防止數組越界，遍歷到n-gap-1{int end = i;int temp = a[end + gap];while (end >= 0){if (temp < a[end]){a[end + gap] = a[end];end -= gap;}else break;}a[end + gap] = temp;}

?單趟多組：

	int gap = 3;//假設gap為3for (int j = 0;j < gap;j++){for (int i = j;i < n - gap;i += gap) //為防止數組越界，遍歷到n-gap-1{int end = i;int temp = a[end + gap];while (end >= 0){if (temp < a[end]){a[end + gap] = a[end];end -= gap;}else break;}a[end + gap] = temp;}}

降低循環層次的辦法：

上面是一組一組來排，下面代碼是每組并發的排序；如果有gap組，那么就從每組的首元素開始遍歷至末尾

	int gap = 3;//假設gap為3for (int i = 0;i < n - gap;i ++) //為防止數組越界，遍歷到n-gap-1{int end = i;int temp = a[end + gap];while (end >= 0){if (temp < a[end]){a[end + gap] = a[end];end -= gap;}else break;}a[end + gap] = temp;}

整體：

void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;for (int j = 0;j < gap;j++){for (int i = j;i < n - gap;i += gap) //為防止數組越界，遍歷到n-gap-1{int end = i;int temp = a[end + gap];while (end >= 0){if (temp < a[end]){a[end + gap] = a[end];end -= gap;}else break;}a[end + gap] = temp;}}}
}

性能分析：

?? ?效率如何被提升的？
?? ?最開始，每個數跳得都很快，這時正好數組最無序；最后一次排序（gap == 1），每個數都跳得很慢，但基本上都不怎么需要動了，都可以break掉
?? ?正是因為希爾排序的這種特性，數據量越大、重復的數據越多（重復數據多，break多挪動少）希爾排序就越是有優勢

?? ?時間復雜度 O(N^1.3)
?? ?gap組數據，假設忽略掉 +1 （方便運算），gap = n/3 同時每組有3個元素（第一組有4個元素，也看作是3個）
?? ?最壞情況下第一趟預排序的消耗：逆序，（1+2）* n / 3 = n (每組的當中元素向前移動1位，后一個元素向前移動2位，總共有n/3組）
?? ?最壞情況下第二趟預排序（gap/3/3 = gap/9）的消耗：逆序，（1+2+3+……+8）* n / 9 = 4n
?? ?然而，第一趟預排序結束以后，就大概率無法形成最壞情況逆序了；所以第二次排序的消耗肯定小于4n，具體是多少此處省略（復變函數相關內容）
?? ?總共進行了log3(N)次這樣的預排序（ +1 依舊省略）

5.選擇排序

選擇排序：每一次從待排序的數據元素中選出最小（或最大）的一個元素，存放在序列的起始位置，直到全部待排序的數據元素排完。

優化：定義一個begin，再定義一個end；每次找到最小的放在begin，找到最大的放在end；放完之后begin++，end--

	int begin = 0, end = n - 1;while (begin < end){//單趟int mini = begin, maxi = begin;for (int i = begin + 1;i <= end;i++){if (a[i] > a[maxi]) maxi = i;if (a[i] < a[mini])mini = i;}Swap(&a[begin], &a[mini]);Swap(&a[end], &a[maxi]);begin++;end--;}

循環起止條件：最大值最小值初始化時都是begin下標元素，因此無需再次進行比較；end位置元素沒被用來初始化，因此需要遍歷到end進行判斷比較大小

代碼問題：如果maxi在begin位置，mini在begin+1位置；那么在第一個交換語句后，maxi位置的值會被覆蓋為最小值；所以需要在 maxi == begin 時，把maxi用mini覆蓋掉（此時mini位置存著最大值，maxi位置存著最小值）

void SelectSort(int* a, int n)
{int begin = 0, end = n - 1;while (begin < end){//單趟int mini = begin, maxi = begin;for (int i = begin + 1;i <= end;i++){if (a[i] > a[maxi]) maxi = i;if (a[i] < a[mini])mini = i;}Swap(&a[begin], &a[mini]);if (maxi == begin) maxi = mini;Swap(&a[end], &a[maxi]);begin++;end--;}
}

6.堆排序

詳見文章：堆復習（C語言版）

void Swap(int* a, int* b)
{int c = *a;*a = *b;//把a地址處的元素變為b位置處的元素*b = c;
}void AdjustDown(int* a, int n, int parent)
{//先假設左孩子小int child = parent * 2 + 1;//如果child >= size（n），說明已經到了葉子節點，停止循環while (child < n){//找出小的那個孩子(先得判斷有沒有右孩子，這也就是假設左孩子小，不假設右孩子小的原因）if (child + 1 < n && a[child + 1] > a[child])child++;//右孩子比較小，改為右孩子//交換or不交換位置,父節點小于小的子節點時，說明找到了該在的位置if (a[parent] >= a[child])break;else{Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}}
}void HPSort(int* a, int n)
{//for (int i = 1; i < n; i++)//Adjustup(a, i); //向上調整建立小堆操作，時間復雜度為nlognfor (int i = (n - 1 - 1) / 2; i >= 0; i--)AdjustDown(a, n, i);//從最后一個父節點開始，依次向下調整，直到調整到根節點為止，時間復雜度為nint end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}
}