在前面我們介紹了堆和二叉樹的基本概念后,本篇文章將帶領大家深入學習鏈式二叉樹。
1.預備知識
2.二叉樹結點的創建
3.二叉樹的遍歷?
3.1前序遍歷
3.2中序遍歷
3.3?后序遍歷
4.統計二叉樹的結點個數
5.二叉樹葉子結點的個數
?6.二叉樹第k層的結點個數
?7.總結
1.預備知識
由于二叉樹的性質,我們在實現二叉樹及其相關功能時會經常使用到遞歸的操作。
所以我們首先介紹一下遞歸算法。
在百度百科中,對于遞歸算法的定義是:某個函數直接或者間接地調用自身,這樣原問題的求解就轉換為了許多性質相同但是規模更小的子問題。
很多同學或許對這句話無法理解,沒有關系。
在這里我們僅僅將其當作一個工具,在編寫代碼時,我們只需搞清楚繁雜的遞歸調用中的一次調用即可,不需要去深究他調用的過程。在文章后續的代碼實現中,大家可以深刻體會到這句話的意思。
2.二叉樹結點的創建
?既然是鏈式二叉樹,對學習過鏈表的大家就很簡單了。直接上代碼
typedef char BTDataType;typedef struct BTreeNode//每一個結點的結構
{BTreeNode* left;//指向左樹BTreeNode* right; //指向右樹BTDataType data;//結點的值
}BTNode;BTNode* BuyNode(BTDataType x)//為新結點開辟空間
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));newnode->data = x;newnode->left = newnode->right = NULL;return newnode;
}3.二叉樹的遍歷?
二叉樹的遍歷有四種:前序遍歷、中序遍歷、后序遍歷、層序遍歷。
今天我們在這里講解前三種遍歷,層序遍歷請看下回分解。
3.1前序遍歷
前序遍歷就是先遍歷根結點,在遍歷左子樹,最后遍歷右子樹。
理解了概念我們直接上代碼。
void PreOrder(BTNode* root)//前序 根 左子樹 右子樹
{if (root == NULL){printf("NULL");return;}else {printf("%c", root->data);//打印根節點PreOrder(root->left);//遞歸遍歷左子樹PreOrder(root->right);//遞歸遍歷右子樹}
}這里我們就使用到了遞歸。該如何理解呢。
我們只關注一次調用,既然遍歷左樹,
那么我們就讓根去找,即?PreOrder(root->left)。
遍歷右樹,即PreOrder(root->right)。
中間是如何進行調用的細節我們不需要深究,我們只需要知道這個遞歸的寫法。剩下的交給計算機。如果大家仍沒理解,可以畫個對照代碼畫一個草圖。
?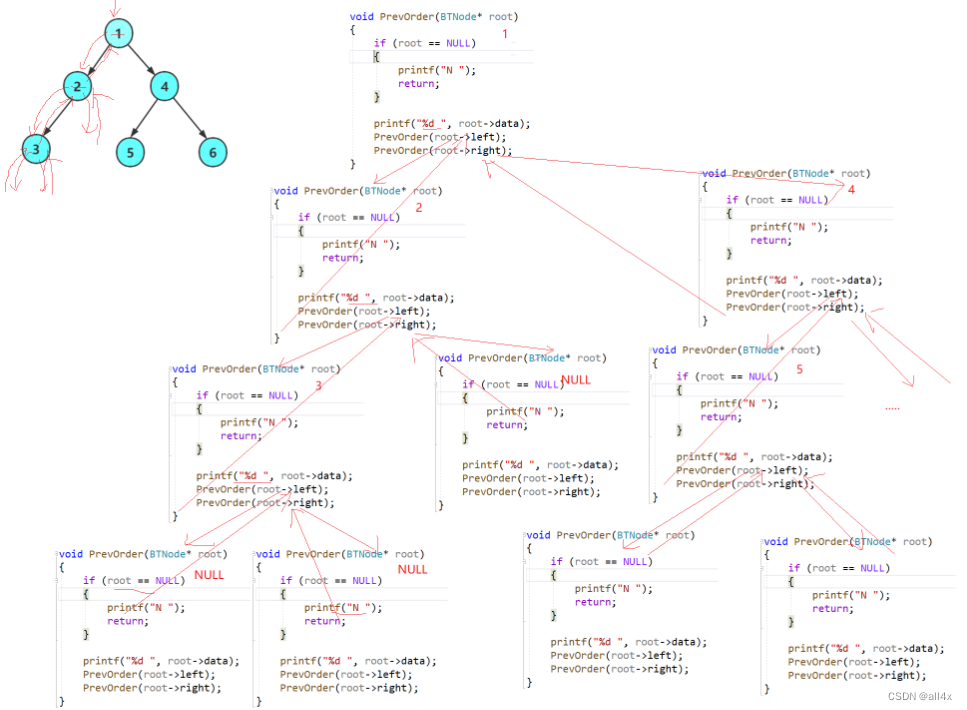
3.2中序遍歷
中序遍歷:先遍歷左子樹,在找根,最后遍歷右子樹。
代碼如下
void InOrder(BTNode* root)
{if (root == NULL){printf("NULL");return;}else {InOrder(root->left);//遍歷左樹printf("%c", root->data);//找根InOrder(root->right);//遍歷右樹}
}這里的遞歸我們仍然按一樣的方法進行理解,只看一層調用。大家可以看圖理解。?
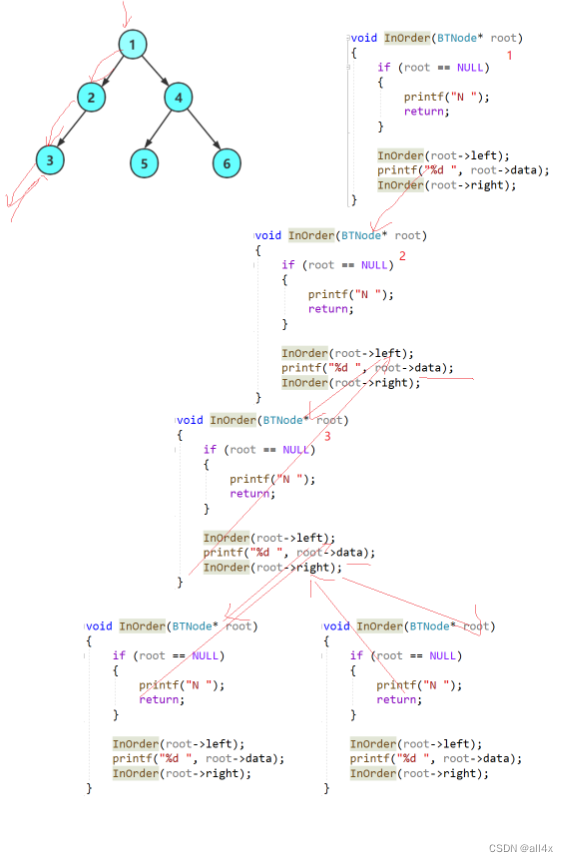
3.3?后序遍歷
后序遍歷:先遍歷左子樹,再遍歷右子樹,最后找根。
void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL");return;}else {PostOrder(root->left);//遍歷左樹PostOrder(root->right);//遍歷右樹printf("%c", root->data);//找根}
}后序的圖大家就自己畫畫吧。?
4.統計二叉樹的結點個數
?如何統計二叉樹的結點個數呢。
思路很簡單,沒遍歷一個非空結點,個數加一。我們看下面代碼。
void TreeSize(BTNode* root)
{if (root == NULL)return;int count = 0;count++;//既然不為空,那么一定就有一個結點的存在TreeSize(root->left);TreeSize(root->right);
}如果大家覺得這個代碼對的話,那就掉入陷阱了!
在遞歸調用中,count存在于棧幀之中,并且遞歸的每一次調用都會開辟新的一塊棧幀,這樣的話我們的count就無法進行值的保存而達到連續的效果。所以這里我們不能這樣進行實現。
下面我們介紹正確的寫法。
void TreeSize(BTNode* root,int*p)//p為指向節點個數的指針
{if (root == NULL)return;++(*p);//結點個數++,既然不為空,那么一定有一個根結點,所以先++TreeSize(root->left, p);//遍歷左子樹的結點TreeSize(root->right, p);//遍歷右子樹的結點
}我們在這里運用定義了一個外部指針變量,用來記錄結點的個數,傳入的是記錄結點個數變量的地址。這樣就可以避免?原來出現的問題了。
?其實這里還有個更加簡單的方法,直接用root來記錄結點個數。
int TreeSize(BTNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}5.二叉樹葉子結點的個數
?既然可以得到結點總數,那葉子結點是不是也可以得到呢。我們先上代碼再解釋。
int BTreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL) //葉子結點的特點{return 1;}return BTreeLeafSize(root->left) + BTreeLeafSize(root->right);//找葉子結點
}既然要找葉子結點首先我們要知道葉子結點的性質:左右子樹均為空。
所以我們在遞歸的時候需要加入葉子結點的判斷條件,如果是葉子結點就要返回。
當然在進行遞歸前要判斷根節點是否存在或者根結點是否有值,我們將其劃分為代碼中的一中情況。
?6.二叉樹第k層的結點個數
我們該如何求任意一層的結點個數呢。
我們將求第k層的結點個數轉化為求第k-1層結點的左右子樹個樹是不是就和我們求葉子結點個數大同小異了呢!
int BTreeLayerSize(BTNode* root,int k)
{if (root == NULL)return 0;if (k == 1)return 1;return BTreeLayerSize(root->left, k - 1) + BTreeLayerSize(root->right, k - 1);
}
我們加入需要的層數k,我們從根結點往下找第k層,如果要使其找到k層,就要使k=1。我們畫圖理解?。

我們假設要求第三層的結點個數,k=3。根結點為第一層,與其匹配的k=3,所以到找到第三層,就要使k--,簡而言之,我們要找到的那一層匹配的k=1。這里可能有點繞,大家可以試著自己畫圖理解?。
?7.總結
?二叉樹的內容到這里并沒有結束,后序的內容需要用到隊列的知識,所以我會在穿插隊列的實現后繼續為大家講解二叉樹的相關知識!敬請期待!



)














)
)