二叉樹

1.數概念及結構

1.1樹的結構

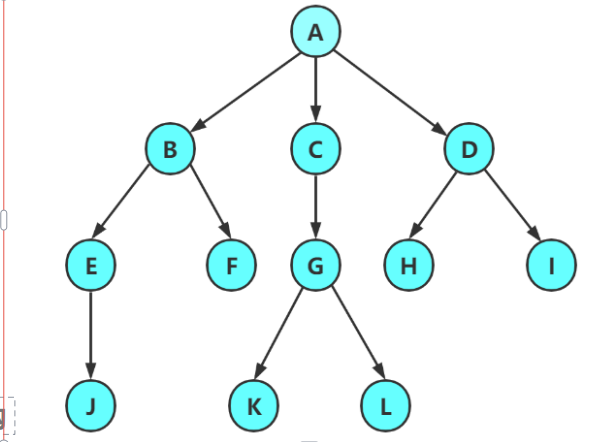
樹是一種非線性的數據結構，它是由n（n>=0）個有限結點組成一個具有層次關系的集合。把它叫做樹是因

為它看起來像一棵倒掛的樹，也就是說它是根朝上，而葉朝下的。

• 有一個特殊的結點，稱為根結點，根節點沒有前驅結點

• 除根節點外，其余結點被分成M(M>0)個互不相交的集合T1、T2、……、Tm，其中每一個集合Ti(1<= i <= m)又是一棵結構與樹類似的子樹。每棵子樹的根結點有且只有一個前驅，可以有0個或多個后繼.

• 因此，樹是遞歸定義的

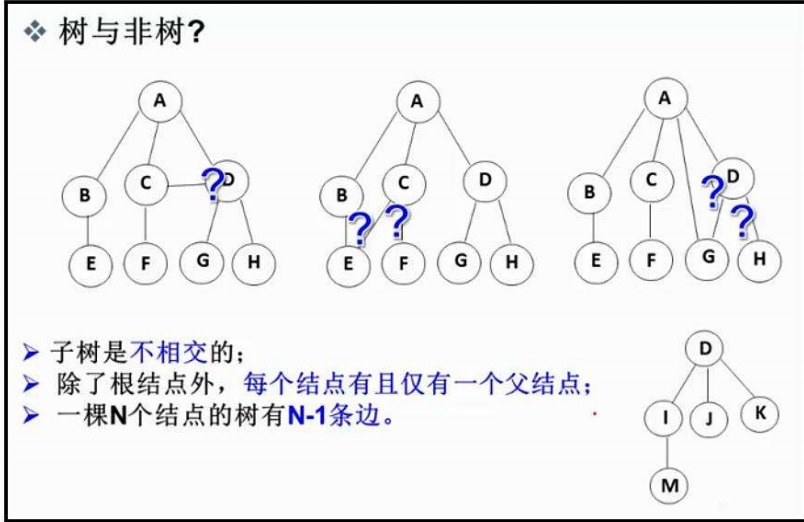
注意：樹形結構中，子樹之間不能有交集，否則就不是樹形結構

1.2樹的相關概念

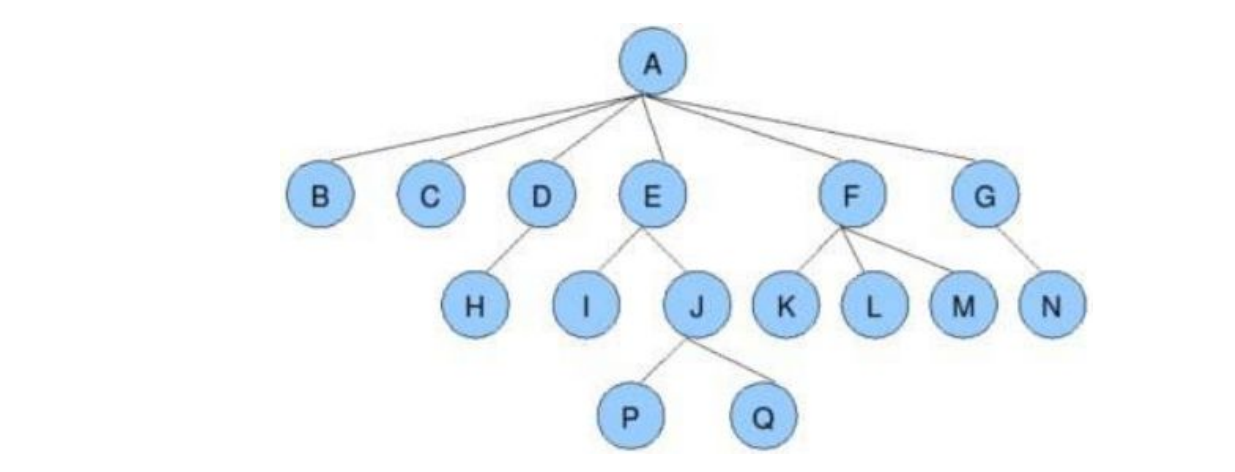
• 節點的度：一個節點含有的子樹的個數稱為該節點的度，如上圖，A的度是6.
• 葉節點或終端節點：度為0的節點稱為葉節點。如B,C,H,P等等
• 非終端節點或分支節點：度不為0的節點； 如上圖：D、E、F、G…等節點為分支節點
• 雙親節點或父節點：若一個節點含有子節點，則這個節點稱為其子節點的父節點； 如上圖：A是B的父節點
• 孩子節點或子節點：一個節點含有的子樹的根節點稱為該節點的子節點； 如上圖：B是A的孩子節點
• 兄弟節點：具有相同父節點的節點互稱為兄弟節點； 如上圖：B、C是兄弟節點
• 樹的度：一棵樹中，最大的節點的度稱為樹的度； 如上圖：樹的度為6
• 節點的層次：從根開始定義起，根為第1層，根的子節點為第2層，以此類推；
• 樹的高度或深度：樹中節點的最大層次； 如上圖：樹的高度為4
• 堂兄弟節點：雙親在同一層的節點互為堂兄弟；如上圖：H、I互為兄弟節點
• 節點的祖先：從根到該節點所經分支上的所有節點；如上圖：A是所有節點的祖先
• 子孫：以某節點為根的子樹中任一節點都稱為該節點的子孫。如上圖：所有節點都是A的子孫
• 森林：由m（m>0）棵互不相交的樹的集合稱為森林

1.3樹的表示

樹結構相對線性表就比較復雜了，要存儲表示起來就比較麻煩了，既然保存值域，也要保存結點和結點之間

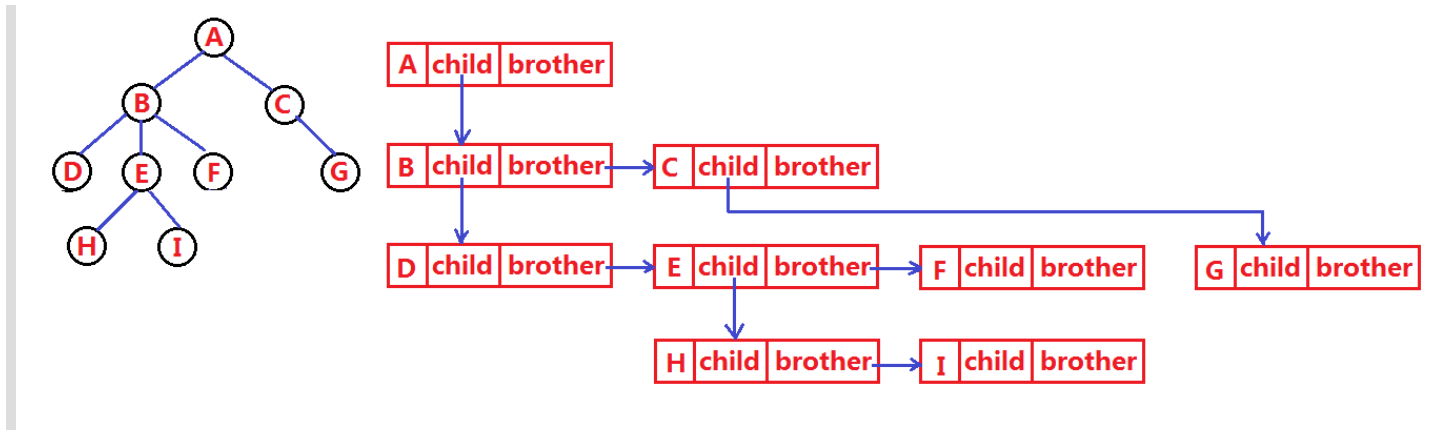
的關系，實際中樹有很多種表示方式如：雙親表示法，孩子表示法、孩子雙親表示法以及孩子兄弟表示法等。我們這里就簡單的了解其中最常用的孩子兄弟表示法。

typedef int DataType;
struct Node
{struct Node* _firstChild1; // 第一個孩子結點struct Node* _pNextBrother; // 指向其下一個兄弟結點DataType _data; // 結點中的數據域
};

其實也可以叫做左孩子右兄弟法

typedef int DataType;
struct Node
{struct Node* _leftChild; // 指向左邊的第一個孩子結點struct Node* _rightBrother; // 指向其右邊的下一個兄弟結點DataType _data; // 結點中的數據域
};

1.4 樹在實際中的運用

表示文件系統的目錄樹結構

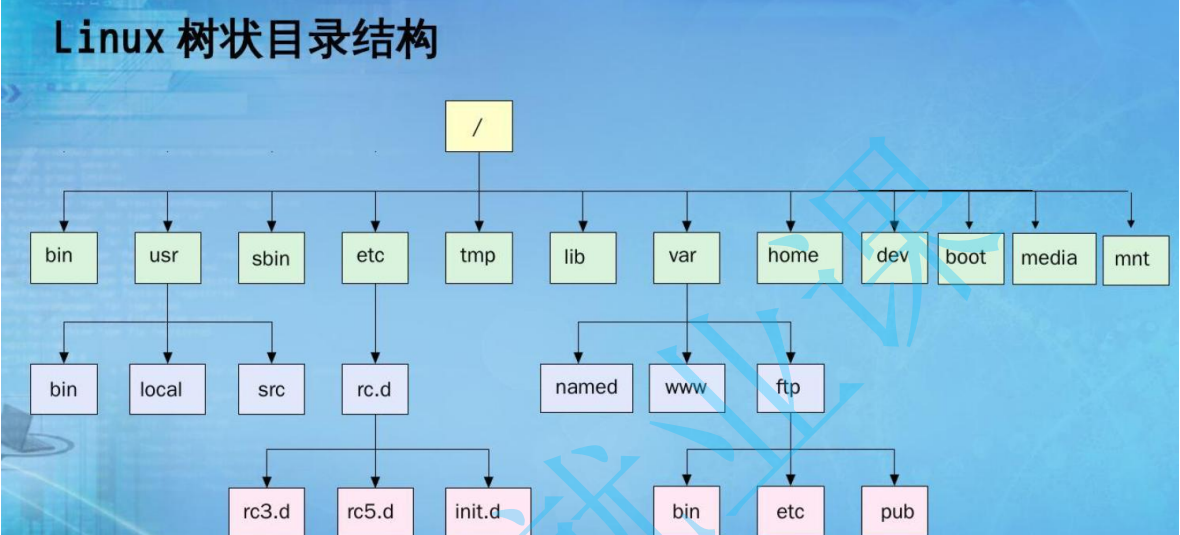
還有就是我們window系統的C盤D盤之類的也是目錄樹結構

2.二叉樹概念及結構

2.1概念

一棵二叉樹是結點的一個有限集合，該集合:

1. 或者為空

2. 由一個根節點加上兩棵別稱為左子樹和右子樹的二叉樹組成

由圖中我們可以知道：

1. 二叉樹不存在度大于2的結點

2. 二叉樹的子樹有左右之分，次序不能顛倒，因此二叉樹是有序樹

注意：對于任意的二叉樹都是由以下幾種情況復合而成的：

2.2特殊的二叉樹

• 滿二叉樹：一個二叉樹，如果每一個層的結點數都達到最大值，則這個二叉樹就是滿二叉樹。也就是說，如果一個二叉樹的層數為K，且結點總數是2^k - 1，則它就是滿二叉樹。

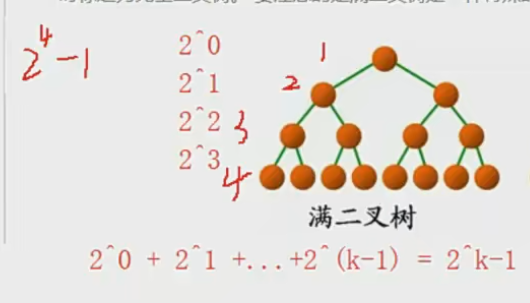
• 完全二叉樹：完全二叉樹是效率很高的數據結構，完全二叉樹是由滿二叉樹而引出來的。對于深度為K的，有n個結點的二叉樹，當且僅當其每一個結點都與深度為K的滿二叉樹中編號從1至n的結點一一對應時稱之為完全二叉樹。要注意的是滿二叉樹是一種特殊的完全二叉樹。

完全二叉樹簡單概括來說就是：前k-1層都必須是滿的，第k層的所有節點從左到右一定得是連續的，可以不滿。

滿二叉樹是完全二叉樹的其中一種情況，完全二叉樹又是二叉樹的其中一種情況，二叉樹又是數的其中一種情況。

2.3二叉樹的性質

1. 若規定根節點的層數為1，則一棵非空二叉樹的第i層上最多有2^(i-1)個節點
2. 若規定根節點的層數為1，則深度為h的二叉樹的最大結點數是2^h - 1個結點
3. 對任何一棵二叉樹, 如果葉結點個數為n0，度為2的分支節點個數是n2，那么有公式n0 = n2 + 1

如圖所示：

• 左邊滿二叉樹的葉結點為8個，度為2的分支節點是7個 。 8 = 7 +1。
• 右邊的完全二叉樹，葉節點是5個，度為2的分支節點是4個。5 = 4 + 1。

4. 若規定根節點的層數為1，具有n個結點的滿二叉樹的深度，h=以2為底的log(n+1)

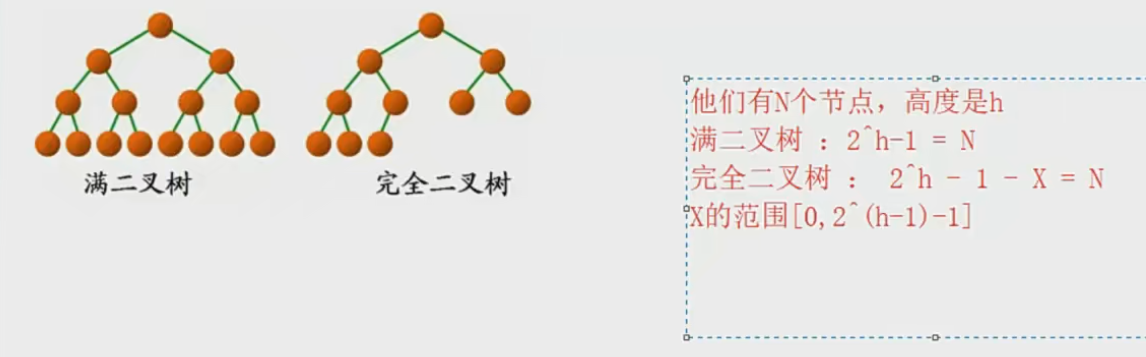
5. 對于具有n個結點的完全二叉樹，如果按照從上至下從左至右的數組順序對所有節點從0開始編號，則對于序號為i的結點有：

• 若i>0，i位置節點的雙親序號：(i-1)/2；i=0，i為根節點編號，無雙親節點

• 若2i+1<n，左孩子序號：2i+1，2i+1>=n否則無左孩子

• 若\2i+2<n，右孩子序號：2i+2，2i+2>=n否則無右孩子

我們來看幾個選擇題：

1.某二叉樹共有 399 個結點，其中有 199 個度為 2 的結點，則該二叉樹中的葉子結點數為（）A 不存在這樣的二叉樹B 200C 198D 199

這道題用前面我們總結的性質可以解決 n0 = n2 + 1。

2.下列數據結構中，不適合采用順序存儲結構的是（）A 非完全二叉樹B 堆C 隊列D 棧

3.在具有 2n 個結點的完全二叉樹中，葉子結點個數為（）A nB n+1 C n-1 D n/2

我們知道n0 = n2 + 1。 我們設葉節點個數為x，那么度為2的節點個數為x -1，這里又是完全二叉樹，可能會存在一個度為1的分支節點，但是總個數又是2n，是偶數，因此這里的度為1的分支結點肯定存在，因此最后的公式就是：x + x - 1 + 1 = 2n

如圖所示，完全二叉樹可能存在度為1的分支節點

4.一棵完全二叉樹的節點數位為531個，那么這棵樹的高度為（）A 11B 10C 8D 12

根據二叉樹的節點數和層數對應的公式就可以解決 ，如果前9層是滿的，即2^9 - 1個 = 255個，第10層可以容納 2^(10-1)個結點，也就是最多512個結點。因此剩下的，531-255 = 276個結點都放在第10層了。

5.一個具有767個節點的完全二叉樹，其葉子節點個數為（）A 383B 384C 385D 386

由于是完全二叉樹，節點總數又是奇數，因此不存在度為1的分支節點。我們設葉結點個數為 x， 則度為2的分支節點的個數是 x -1. 因此：x + x - 1 = 767.

x = 384。

答案：B A A B B

2.4 二叉樹的存儲結構

二叉樹一般可以使用兩種結構存儲，一種順序結構，一種鏈式結構

2.4.1順序存儲

順序結構存儲就是使用數組來存儲，一般使用數組只適合表示完全二叉樹，因為不是完全二叉樹會有空間的浪費。而現實中使用中只有堆才會使用數組來存儲，關于堆我們后面的章節會專門講解。二叉樹順序存儲在物理上是一個數組，在邏輯上是一顆二叉樹。

如圖所示

如果我們用數組來表示樹，我們需要將樹的節點的通過下標來記載到數組中，但是如果不是完全二叉樹的話，數組就會浪費非常多的空間。數組必須有很多空著不用的空間，代表這個地方沒有數節點。

如果是完全二叉樹的話，就會非常高效，不僅僅是數組的空間上沒有浪費，而且數組的下標非常有規律，很好找到二叉樹對應的樹節點

• 父親的節點下標是 i
• 該父親節點的左孩子的節點的下標是 2 * i + 1 。
• 該父親節點的右孩子的節點的下標是 2 * i + 2 。

不僅可以通過父親節點下標算孩子節點下標，還可以通過孩子節點下標算父親節點的下標。

• 孩子的節點下標是 i
• 父親的節點下標是 (i - 1) / 2 【這樣兩個孩子都能找到自己的父親】

2.4.2鏈式存儲

二叉樹的鏈式存儲結構是指，用鏈表來表示一棵二叉樹，即用鏈來指示元素的邏輯關系。通常的方法是鏈表中每個結點由三個域組成，數據域和左右指針域，左右指針分別用來給出該結點左孩子和右孩子所在的鏈結點的存儲地址。鏈式結構又分為二叉鏈和三叉鏈，當前我們學習中一般都是二叉鏈，后面課程學到高階數據結構如紅黑樹等會用到三叉鏈。

我們來和這兩個結構“打個招呼”。

typedef int BTDataType;
// 二叉鏈
struct BinaryTreeNode
{struct BinTreeNode* _pLeft; // 指向當前節點左孩子struct BinTreeNode* _pRight; // 指向當前節點右孩子BTDataType _data; // 當前節點值域
}
// 三叉鏈
struct BinaryTreeNode
{struct BinTreeNode* _pParent; // 指向當前節點的雙親struct BinTreeNode* _pLeft; // 指向當前節點左孩子struct BinTreeNode* _pRight; // 指向當前節點右孩子BTDataType _data; // 當前節點值域
}；

3.二叉樹的順序結構及實現

3.1二叉樹的順序結構

前面我們也提到過，普通的二叉樹是不適合用數組來存儲的，因為可能會存在大量的空間浪費。而完全二叉樹更適合使用順序結構存儲。

現實中我們通常把堆(一種二叉樹)使用順序結構的數組來存儲，需要注意的是這里的堆和操作系統虛擬進程地址空間中的堆是兩回事，一個是數據結構，一個是操作系統中管理內存的一塊區域分段。

這里需要知道，堆的邏輯結構是完全二叉樹，是非線性的，但是堆的底層是用數組實現的，因此物理結構上是線性的

我們來看一個圖片，可以更好的理解在數組中存儲的完全二叉樹：

但是這個數組里面存儲的是一個完全二叉樹，但是它不是堆、數組建堆主要依靠的就是——向下調整算法【前提是左右子樹是對應的堆】

3.2堆的概念及結構

堆的性質：

• 堆中某個節點的值總是不大于或不小于其父節點的值
• 堆 總是一個完全二叉樹

我們來看看大堆和小堆的圖：

知道了堆的相關知識后，我們可以來做點選擇題：

1.下列關鍵字序列為堆的是：（）
A 100,60,70,50,32,65
B 60,70,65,50,32,100
C 65,100,70,32,50,60
D 70,65,100,32,50,60
E 32,50,100,70,65,60
F 50,100,70,65,60,322.已知小根堆為8,15,10,21,34,16,12，刪除關鍵字 8 之后需重建堆，在此過程中，關鍵字之間的比較次
數是（）。
A 1
B 2
C 3
D 43.一組記錄排序碼為(5 11 7 2 3 17),則利用堆排序方法建立的初始堆為
A(11 5 7 2 3 17)
B(11 5 7 2 17 3)
C(17 11 7 2 3 5)
D(17 11 7 5 3 2)
E(17 7 11 3 5 2)
F(17 7 11 3 2 5)4.最小堆[0,3,2,5,7,4,6,8],在刪除堆頂元素0之后，其結果是（）
A[3，2，5，7，4，6，8]
B[2，3，5，7，4，6，8]
C[2，3，4，5，7，8，6]
D[2，3，4，5，6，7，8]

答案是：

A C C C

3.3堆的實現

我們這里實現的是 ----小堆-----

#pragma once
#define  _CRT_SECURE_NO_WARNINGS 1
# include<stdio.h>
# include<stdlib.h>
# include<assert.h>
# include<string.h>// 這里我們實現的是  小堆// 定義堆的結構
typedef int HPDatatype;
typedef struct Heap
{HPDatatype* _a; // 堆是用數組存儲的(這里用動態順序表)int _size;int _capacity; 
}Heap;// 堆的接口// 樹節點的調換
void Swap(HPDatatype* child, HPDatatype* parent);// 堆向下調整算法
void AdjustDown(HPDatatype* a, int n, int root);// 堆的初始化
void HeapInit(Heap* php, HPDatatype* a, int n);// HPDatatype* a就是一個存放數據的數組的指針// 堆的排序
void HeapSort(HPDatatype* a, int n);// 堆的銷毀
void HeapDestory(Heap* php);// 向上調整算法
void AdjustUp(HPDatatype* a, int n, int child);// 堆的插入
void HeapPush(Heap* php, HPDatatype x);// 堆的刪除 【這里刪除的數據是要刪除堆頂的數據】
void HeapPop(Heap* php);// 堆的打印
void HeapPrint(Heap* php);// 獲取堆頂的數據
HPDatatype HeapTop(Heap* php);// 獲取堆的數據個數
int HeapSize(Heap* php);// 判斷堆是否為空
int HeapEmpty(Heap* php); // 是空的就返回1 不是空的就返回0

在實現堆之前，我們要先學習堆向下調整算法，才能實現堆。

我們這里實現的是小堆

3.3.1堆向下調整算法

現在我們給出一個數組，邏輯上看做一顆完全二叉樹。我們通過從根節點開始的向下調整算法可以把它調整成一個小堆。向下調整算法有一個前提：左右子樹必須是一個堆，才能調整。

int array[] = {27,15,19,18,28,34,65,49,25,37};

由于我們實現的是小堆，我們假設堆頂的數據是27，那么他就會去和左孩子去對比，假如比左孩子大，那么就會互換位置，然后再去和左孩子去對比 。以此類推…

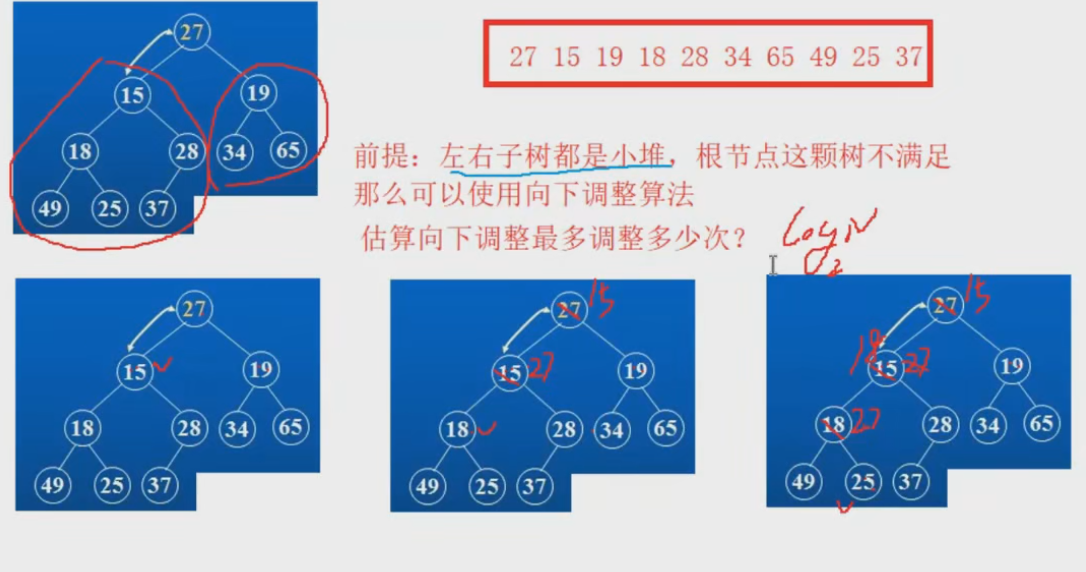
那我們來看看這個算法和思路要如何通過代碼實現呢？

如圖所示，我們雖然是在對樹進行操作，但是實際上我們是在對數組進行操作。因此我們需要通過操作數組的下標來實現我們的堆向下調整算法。

而前面我們學習過，在完全二叉樹中，想找到父節點的左孩子的和右孩子都是有對應的公式的。 那就是 父節點下標 * 2 + 1 或者 父節點下標 * 2 + 2，對應找到左孩子和右孩子

我們來看看代碼如何實現：

void Swap(HPDatatype* child, HPDatatype* parent)
{HPDatatype tmp = *parent;*child = *parent;*parent = tmp;
}// 前提：左右子樹都是小堆
void AdjustDown(HPDatatype* a, int n, int root) // root是傳進來結點的下標, n是數組的元素個數
{int parent = root; // 既然要向下調整，那傳進來的節點就是父節點，讓其和孩子節點去對比int child = parent * 2 + 1; // 默認是左孩子// 交換可能要交換很多次，因此只要孩子節點的下標沒有超出最后一個節點的下標，就不能退出循環while (child < n){// 判斷左右孩子誰更小  if (child + 1 < n && a[child] > a[child + 1]) // 要注意如果只有左孩子沒有右孩子，那么要小心child + 1會越界，因此需要child + 1也小于n{child++;// 如果右孩子小，那就讓孩子更改成右孩子}// 現在要讓父節點和孩子節點對比// 現在孩子節點是左右孩子節點中最小的，讓其和父節點進行對比if (a[parent] > a[child]){// 如果父節點大，就交換Swap(&a[child], &a[parent]);// 由于不止交換一次，因此需要迭代，更新child和parent節點parent = child; // 交換完之后父親節點交換到孩子節點了。child = child * 2 + 1;  // 讓孩子節點指向新的孩子節點， 默認左孩子 }else{// 走這里說明父節點小于孩子節點，那就不用再交換了。break;}}}

但是，我們知道，使用這個算法的前提是：左右子樹都是小堆。

因此我們還需要將左右子樹先搞成小堆先

3.3.2堆的創建

下面我們給出一個數組，這個數組邏輯上可以看做一顆完全二叉樹，但是還不是一個堆，現在我們通過算法，把它構建成一個堆。根節點左右子樹不是堆，我們怎么調整呢？這里我們從倒數的第一個非葉子節點的子樹開始調整，一直調整到根節點的樹，就可以調整成堆

其實原始一點的思路是這樣的，我們既然知道要將左右子樹都弄成堆，但是左右子樹又有可能有下一個左右子樹，因此不如直接從數組的最后一個元素下標開始調整，也就是從葉子結點開始調整【其實不用調整】，這樣走到第一個父節點就可以順利使用堆向下調整算法，以此類推。 我們可以來看一個圖：

這樣子我們在調整倒數的子樹的時候其左右子樹都是堆的形式出現。就可以保證前提：左右子樹都是堆

這樣思路下的代碼是這樣的：

	// 建堆for (int i = n - 1; i >= 0; i--) {// 從最后一個子樹開始調整 【葉節點可以看做是一個度為0的子樹】AdjustDown(a, n, i);}

但是我們發現，對葉節點進行堆向下調整算法，是沒有意義的，因此我們可以通過找到倒數第一個父節點，也就是從倒數的第一個非葉子節點的子樹開始調整，一直調整到根節點的樹，就可以調整成堆

我們來看看代碼是如何實現的：

	// 構建堆（向下調整算法[前提是：左右子樹都是小堆]）// 因此我們要先把左右子樹搞成小堆  如何搞呢？ 其實從樹中最小的子樹開始調整就行for (int i = (n - 1 - 1) / 2; i >= 0; i--) // (n - 1 - 1) / 2 找到的就是倒數第一個父節點{AdjustDown(php->_a, n, i); // 從倒數第一個子樹開始調整成小堆，讓每一個子樹都變成小堆}

我們現在已經知道了一個堆要如何創建出來了，那我們來看看堆的初始化代碼。

先知道堆的創建過程，再去看初始化過程，會比較好理解。

3.3.3堆的初始化代碼：

// 堆的初始化
void HeapInit(Heap* php, HPDatatype* a, int n) // HPDatatype* a就是一個存放數據的數組的指針
{// 給數組開辟n個大小為HPDatatype的空間 php->_a = (HPDatatype*)malloc(sizeof(HPDatatype) * n);if (php->_a == NULL){perror("HeapInit():malloc()");exit(-1);}// 往堆中存放數據memcpy(php->_a, a, sizeof(HPDatatype) *n);// 意思是說從a這個指針處，傳遞sizeof(HPDatatype)* n個字節到php->_a處php->_size = n;php->_capacity = n;// 這個時候只是把數據放進了數組中，但是還不是堆// 不僅僅要把數據存放進去，還要將里面的數據變成堆的形式去存放// 構建堆（向下調整算法[前提是：左右子樹都是小堆]）// 因此我們要先把左右子樹搞成小堆  如何搞呢？ 其實從樹中最小的子樹開始調整就行for (int i = (n - 1 - 1) / 2; i >= 0; --i) // (n - 1 - 1) / 2 找到的就是倒數第一個父節點{AdjustDown(php->_a, php->_size, i); // 從倒數第一個子樹開始調整成小堆，讓每一個子樹都變成小堆}}

測試代碼：

int main()
{// 給一個完全二叉樹int array[] = { 27,15,19,18,28,34,65,49,25,37 };Heap hp;HeapInit(&hp, array, sizeof(array) / sizeof(array[0]));return 0;
}

經過調試，該二叉樹已經變成了小堆。如圖所示：

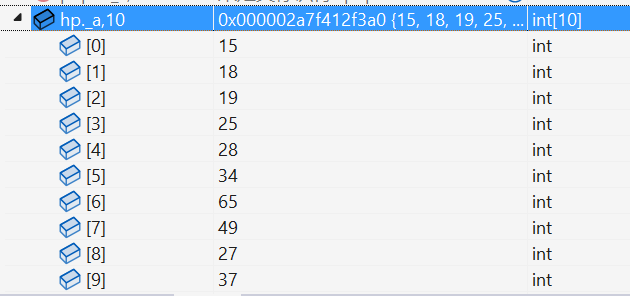
哪怕是給一個很亂的完全二叉樹，也能實現小堆的創建。

用這樣方式會更加直觀：

3.3.4堆棧的時間復雜度

因為堆是完全二叉樹，而滿二叉樹也是完全二叉樹，此處為了簡化使用滿二叉樹來證明(時間復雜度本來看的是近似值，多幾個節點不影響最終結果

	// 構建堆（向下調整算法[前提是：左右子樹都是小堆]）for (int i = (n - 1 - 1) / 2; i >= 0; i--) {AdjustDown(php->_a, n, i); // 從倒數第一個子樹開始調整成小堆，讓每一個子樹都變成小堆}

這里的時間復雜度？
如果樹有N個節點，樹的高度就是：logN （以2為底）
那么一次向下調整算法的時間復雜度就是 logN
但是要注意 這里的時間復雜度不是 N*logN

如果是AdjustDown(a, n, 0);就是N * logN 因為從根結點開始

實際的時間復雜度需要我們來計算和分析：

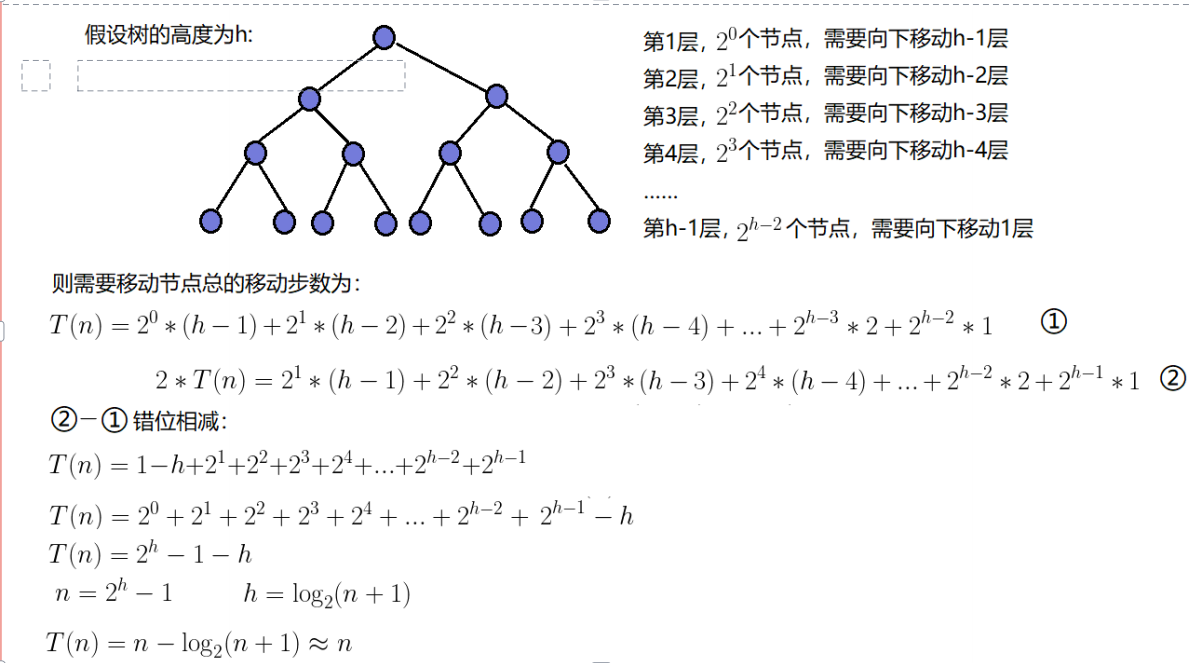
我們假設一個節點調用向下調整算法的移動步數取決于當前所處的高度。

因此：建堆的時間復雜度為O(N)

3.3.5堆的排序

對上面的建堆有了一定的了解和學習之后，我們現在已經能夠構建出一個堆了。

但是這個堆還不是有序的，那我們如果想搞一個有序的小堆或者是大堆要怎么做呢

我們可以通過讓每一個節點都去建堆，這樣每一個節點都是當前樹的最小值/最大值，這樣就可以實現升序/降序。

但是這樣的時間復雜度就是 O（N^2）。 每次建堆的時間復雜度是： O（N），讓每個節點都去建堆。就是O（N^2）

因此我們可以采用一個方法，效率較高的：

我們先看圖：

經過一次這樣的處理，我們可以選出一個次小的數，然后讓次小的數換到倒數第二個位置，堆的大小變成n-2.

然后繼續處理，以此類推。這樣我們的數組存放的就是降序的堆、

這里我們是通過向下調整算法去選出一個樹里面最小的數的，因為向下調整的樹是小堆，小堆的堆頂是該子樹的最小數字。

我們也知道向下調整算法的時間復雜度是O(logN)，因此通過這個方式我們的時間復雜度是 O(N * logN)。因為我們一共需要調整N次。

比時間復雜度O（N^2）的效率高了非常多。

N越大，優勢就會越大。

代碼實現：

	
void HeapSort(HPDatatype* a, int n)
{// 構建堆（向下調整算法[前提是：左右子樹都是小堆]）// 如果樹有N個節點，樹的高度就是：logN （以2為底）// 那么一次向下調整算法的時間復雜度就是 logN// 可以通過計算得知這里的時間復雜度是： O（N）for (int i = (n-1 - 1) / 2; i >= 0; i--) // (n-1 - 1) / 2 找到的就是倒數第一個父節點 第一個n-1是其孩子節點下標{AdjustDown(a, n, i); // 從倒數第一個子樹開始調整成小堆，讓每一個子樹都變成小堆}// 走到這里數組a存儲的完全二叉樹已經是一個小堆了。// 此時的堆還不是有序的// 排序int end = n - 1; // end表示倒數第一個節點的下標while (end > 0){// 交換，把堆頂（最小的數）放到最后面去，然后忽略掉Swap(&a[end], &a[0]);// 調用堆向下調整算法AdjustDown(a, end, 0); // 讓堆頂（下標為0）變成次小的數// 這里的end是當做a數組的元素個數傳進去的，最后一個元素不會參與比較end--; // 忽略掉最后面那個最小的數}// 由于我們的堆構建，構建的是小堆，因此這里的堆排序排出來是降序// 如果我們想要排升序，就構建大堆就行了。}

測試代碼：

int main()
{int array[] = { 27,15,19,18,28,34,65,49,25,37 };HeapSort(array, sizeof(array) / sizeof(array[0]));for (int i = 0; i < 10; i++){printf("%d ", array[i]);}printf("\n");// // 構建小堆 排降序：65 49 37 34 28 27 25 19 18 15 // 構建大堆 排升序：15 18 19 25 27 28 34 37 49 65return 0;
}

構建大堆只需要在向下調整算法的時候，把兩個小于號改成大于號就好了

if (child + 1 < n && a[child] < a[child + 1]) 
{child++;
}
// 現在要讓父節點和孩子節點對比
// 現在孩子節點是左右孩子節點中最大的，讓其和父節點進行對比
if (a[parent] < a[child])
{// 如果父節點小，就交換Swap(&a[child], &a[parent]);// 由于不止交換一次，因此需要迭代，更新child和parent節點parent = child; child = child * 2 + 1;  
}

這樣就行了，其他地方不需要有任何的變化~

3.3.6堆的銷毀

我們需要將我們申請的動態內存空間釋放掉，也就是數組的空間。

代碼如下：

void HeapDestory(Heap* php)
{assert(php); // 如果php是NULL還怎么銷毀free(php->_a);php->_a = NULL;php->_size = php->_capacity = 0;}

3.3.7堆的插入

堆的插入，不能是頭插，不僅效率低下【因為是數組實現】，而且會導致父親節點和孩子節點的關系全亂了。

因此我們需要尾插到堆中，但是堆既然稱之為堆，那就是因為堆有其性質，因此插入數據之后不能不管它，我們需要去調整它，保證我們堆的性質不變。

插入數據會有兩種情況：

• 第一種就是插入后，數據剛好不會改變堆的性質，比如小堆，插入的數據，剛好比父親節點大，那么此時無需改變
• 第二種，就是插入后數據改變了堆的性質，比如，在小堆插入的數據，比父親節點小，這個時候我們就需要去調整它

既然如此，我們就需要先編寫一個向上調整算法。

3.3.7.1向上調整算法

如圖所示，就是讓這個插入節點去和父親節點對比，如果小于父親節點就交換，一直交換到符合小堆的性質為止。

代碼如下:

// 向上調整算法
void AdjustUp(HPDatatype* a, int n, int child)
{// 找父親節點int parent = (child - 1) / 2;while (child > 0) // 當孩子節點 == 0 的時候，就說明已經交換到堆頂了，無需在比較了// 注意這里的條件不能是 parent >= 0 因為parent永遠不可能 < 0。因為parent是int類型 當child = 0的時候，parent = (child - 1) / 2 還是等于0{// 判斷父親節點和孩子節點誰大if (a[child] < a[parent]){// 孩子節點小就交換Swap(&a[child], &a[parent]);// 迭代，更新孩子節點和父親節點的下標child = parent;parent = (child - 1) / 2;}else{break;}}}

知道了向上調整算法之后，我們來看看堆的插入

3.3.7.2 堆的插入

代碼如下：

// 堆的插入
void HeapPush(Heap* php, HPDatatype x)
{assert(php);// 先將其插入到數組的最后一個位置。也就是尾插到堆內，讓完全二叉樹多出一個葉結點// 要先判斷是否有足夠的空間if (php->_capacity == php->_size){// 增容 (增2倍)int newcapacity = php->_capacity == 0 ? 4 : php->_capacity * 2;HPDatatype* tmp = (HPDatatype*)realloc(php->_a, sizeof(HPDatatype) * newcapacity);if (tmp == NULL){perror("HeapPush():realloc()");exit(-1);}// 更新php->_a = tmp;php->_capacity = newcapacity;}// 走到這里空間足夠插入了// 插入php->_a[php->_size] = x; // php->_size如果空間不夠是會越界的php->_size++;// 插入數據之后，不能不管，我們還要保持這個堆的性質。// 這個數據插入進去可能剛好還是小堆，也有可能導致不是小堆了// 因此這里需要一個 向上調整算法 【如果插入的數很小，就要讓其往上走[因為我們實現的是小堆]】AdjustUp(php->_a, php->_size, php->_size - 1);//php->_size - 1 是插入數據的下標}

測試代碼：

	// 堆的插入HeapPush(&hp, 10);HeapPush(&hp, 11);HeapPush(&hp, 12);//HeapSort(hp._a, hp._size);for (int i = 0; i < hp._size; i++){printf("%d ", hp._a[i]);}printf("\n");

測試代碼執行結果如下：

10 15 11 25 18 12 65 49 27 37 28 34 19

這樣看更加清晰，我們的堆在插入數據之后仍然是小堆，雖然不是有序，但是想讓其有序，只需要調用一次堆排序函數就行。

3.3.8 堆的打印

這個非常簡單，根據堆自帶的size，去打印就行

代碼如下：

// 堆的打印
void HeapPrint(Heap* php)
{assert(php);assert(php->_size > 0); // 沒有數據，還打印個集貿for (int i = 0; i < php->_size; i++){printf("%d ", php->_a[i]);}printf("\n");
}

3.3.9堆的刪除

這里的堆的刪除，指的是將堆的堆頂的數據刪除。

但是不能直接讓數組后面的數據往前面覆蓋，因為這樣子不僅時間復雜度是O(N),而且會導致父節點和孩子節點的關系全部打亂！

因此這里我們采取和堆排序類似的思路

• 首先讓堆頂數據和堆最后的數據交換
• 然后size–，這樣就相當于刪除
• 然后對堆頂使用一次堆向下調整算法

知道了思路之后，我們來看看代碼是如何實現的：

// 堆的刪除
void HeapPop(Heap* php)
{assert(php);assert(php->_size > 0); // 如果堆都沒有數據，還刪除個dan// 交換堆頂和最后一個節點Swap(&php->_a[0], &php->_a[php->_size - 1]); // php->_size - 1 就是最后一個數據的下標// 刪除堆頂數據php->_size--;// 對堆頂使用堆向下調整算法AdjustDown(php->_a, php->_size, 0);
}

測試代碼：

	//10 15 11 25 18 19 65 49 27 37 28 34	// 堆的刪除HeapPop(&hp);HeapPop(&hp);HeapPrint(&hp); // 15 18 19 25 28 34 65 49 27 37

可以看到刪除了10 和 11 說明刪除的都是堆頂的數據，并且每刪除一次，到堆頂上去的數據都是次小的數據

3.3.10堆頂數據的獲取

這個也非常簡單。代碼如下：

// 獲取堆頂的數據
HPDatatype HeapTop(Heap* php)
{assert(php);assert(php->_size > 0);return php->_a[0];
}

• 這里有個拓展問題，堆的TopK問題。

3.3.11堆的數據個數

很簡單，代碼如下：

// 獲取堆的數據個數
int HeapSize(Heap* php)
{assert(php);return php->_size;
}

3.3.12堆的判空

很簡單，代碼如下：

// 判斷堆是否為空
int HeapEmpty(Heap* php) // 是空的就返回1 不是空的就返回0
{if (php->_size == 0)return 1;elsereturn 0;
}

3.4堆的應用

3.4.1堆的排序

在前面的3.3.5講的很清楚是如何實現的。

3.4.2堆的TopK問題

TOP-K問題：即求數據結合中前K個最大的元素或者最小的元素，一般情況下數據量都比較大。

意思就是選出堆的 前K個 最小的/最大的 數。

第三個思路的時間復雜度是 O(N+ logK) 如果k很小，那近似于O(N)

其實就是建一個k個數的大堆或者小堆，

• 如果我們要找最大的前k個數，那就要建小堆
• 如果我們要找最小的前k個數，那就要建大堆

這個非常重要，假設我們要找最大的前k個數，那么我們建k個數的小堆，然后讓數去進堆，能進去的說明肯定比堆頂大。因此最后留在這個k個數的小堆里面的數，就是最大的k個數，堆頂的是就是第k大的數。

假設我們要找最小的前k個數，我們就要建k個數的大堆，讓數去和堆頂判斷，只要比堆頂小，那我就進堆，這樣子的話，最小的前k個數最后都會留在這個大堆中，堆頂就是第k小的數。

我們來看一道有關TopK的面試題：

面試題 17.14. 最小K個數

設計一個算法，找出數組中最小的k個數。以任意順序返回這k個數均可。

示例：

輸入： arr = [1,3,5,7,2,4,6,8], k = 4
輸出： [1,2,3,4]

提示：

• 0 <= len(arr) <= 100000
• 0 <= k <= min(100000, len(arr))

思路就是我們前面所講的思路

代碼如下:

void AdjustDown(int* a, int n, int root)
{// 找到孩子節點和父節點int parent = root;int child = parent*2 + 1; //默認是左孩子最大// 可能不止比較一次while(child < n){// 判斷是右孩子大還是左孩子大if(child + 1 < n && a[child + 1] > a[child]){child++;}// 讓父節點去和最大的孩子去比較if(a[parent] < a[child]){// 孩子比父親大，那就交換int tmp = a[child];a[child] = a[parent];a[parent] = tmp;// 迭代。parent = child;child = parent * 2 + 1; // ，默認左孩子}else{break;}} 
}int* smallestK(int* arr, int arrSize, int k, int* returnSize)
{*returnSize = k;// 如果k是0 就說明不再需要操作了if(k == 0)return NULL;int* retArr = (int*)malloc(sizeof(int) * k); // 首先我們先傳k個數據到我們的數組中for(int i = 0; i < k; i++){retArr[i] = arr[i];}// 這個時候的數據還不是堆// 由于我們要找最小的前k個數，因此我們需要建立一個大堆for(int i = (k-1 - 1)/2; i >= 0; i--)//  (k-1 - 1)/2是倒數第一個父節點{AdjustDown(retArr, k, i);}// 此時retArr是一個大堆。但是里面還不是arr里面最小的前k個數// 我們讓后面的數據不斷的去和我們retArr的堆頂去比較，一旦比堆頂小，那就進堆// 這樣最后的堆里面剩下的，就是最小的k個數for(int i = k; i< arrSize; i++){// 讓arr里面的數據和 我們的大堆的堆頂去比較if(arr[i] < retArr[0]){// 比堆頂小就進堆retArr[0] = arr[i];// 但是這個數據成為堆頂之后，可能會破壞大堆// 因此我們需要讓其保持大堆 讓小的往下走AdjustDown(retArr, k, 0);}}// 走到這里，最小的前k個數就已經被我們選出來了return retArr;}

4.二叉樹鏈式結構的實現

#pragma once
#define  _CRT_SECURE_NO_WARNINGS 1
# include<stdio.h>
# include<stdlib.h>
# include<assert.h>// 我們使用鏈式結構實現二叉樹
// 定義一個二叉樹節點的結構體typedef char BTDataType;
typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;
}BTNode;// 申請二叉樹的節點
BTNode* BTNodeCreate(BTDataType x);// 二叉樹前序遍歷
void PreOrder(BTNode* root);// 二叉樹中序遍歷
void InOrder(BTNode* root);// 二叉樹后序遍歷
void PostOrder(BTNode* root);// 層序遍歷 (借助隊列)
void LevelOrder(BTNode* root);// 獲取二叉樹節點個數
int BinaryTreeSize(BTNode* root);// 獲取二叉樹葉子節點個數
int BinaryTreeLeafSize(BTNode* root);// 獲取二叉樹的深度
int BinaryTreeDepth(BTNode* root);// 獲取二叉樹第k層節點個數
int BinaryTreeLevelKSize(BTNode* root, int k);// 二叉樹查找值為x的節點
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);// 判斷二叉樹是否是完全二叉樹 （是就返回1 不是就返回0）
int BinaryTreeComplete(BTNode* root);// 通過前序遍歷的數組"ABD##E#H##CF##G##"構建二叉樹
BTNode* BinaryTreeCreate(BTDataType* a, int* pi);// 二叉樹銷毀
void BinaryTreeDestory(BTNode* root);

4.1前置聲明

此處手動快速創建一棵簡單的二叉樹，快速進入二叉樹的操作學習，等二叉樹結構了解的差不多時，我們反過頭再來研究二叉樹真正的創建方式。

申請二叉樹節點的函數：

// 申請二叉樹的節點
BTNode* BTNodeCreate(BTDataType x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("BTNodeCreate():malloc()");exit(-1);}newnode->_data = x;newnode->_left = NULL;newnode->_right = NULL;
}

創建一顆偽樹：

int main()
{// 我們這里創建一顆偽樹 這里的代碼并不是創建二叉樹的方式BTNode* A = BTNodeCreate('A');BTNode* B = BTNodeCreate('B');BTNode* C = BTNodeCreate('C');BTNode* D = BTNodeCreate('D');BTNode* E = BTNodeCreate('E');// 將其鏈接起來成為一顆樹A->_left = B;B->_left = D;B->_right = E;A->_right = C;return 0;
}

4.2二叉樹的遍歷

4.2.1前序、中序以及后序遍歷

學習二叉樹結構，最簡單的方式就是遍歷。所謂二叉樹遍歷(Traversal)是按照某種特定的規則，依次對二叉樹中的節點進行相應的操作，并且每個節點只操作一次。訪問結點所做的操作依賴于具體的應用問題。 遍歷是二叉樹上最重要的運算之一，也是二叉樹上進行其它運算的基礎。

如圖所示，我們先來看看前序遍歷：

前序遍歷的順序是： 根——左子樹——右子樹

遍歷的思路是：

先訪問A這個根結點，然后去找A結點的左子樹，找到了B這個根結點，然后去找B的左子樹，找到了D這個根結點，再去找D的左子樹，發現找不到就退回去，然后去找D的右子樹，然后也找不到，這個時候B的左子樹訪問完了。要去訪問B的右子樹，找到了E這個根結點，然后去找E的左子樹，找不到，找E的右子樹還是找不到，B的右子樹訪問完了。此時A的左子樹也訪問完了，這個時候訪問A的右子樹，找到C這個根節點，去找C的左子樹，找不到，找右子樹，找不到。此時A的左子樹右子樹都訪問結束。

遍歷結束

A——B——D——NULL——NULL——E——NULL——NULL——C——NULL——NULL

ABDEC

我們來看前序的代碼實現：

// 二叉樹前序遍歷 [根 左子樹 右子樹]
void PreOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%c ", root->_data); // 訪問根PreOrder(root->_left); // 訪問左子樹PreOrder(root->_right); // 訪問右子樹// 多路遞歸，這里是 2路遞歸
}

代碼中使用遞歸的過程如下圖所示：

中序遍歷和后序遍歷：

中序遍歷的順序是： 左子樹——根——右子樹

遍歷思路是這樣的：

要想訪問A這個根節點，需要先訪問根的左子樹，找到了B節點，但是要訪問B節點要先訪問B的左子樹，找到了D結點，但是要先訪問D節點的左子樹

沒找到節點，就訪問D節點，然后訪問D結點的右子樹，沒找到。此時B結點的左子樹訪問完了，那就訪問B節點，然后去找B節點的右子樹，找到了E節點，但是訪問E節點之前，要先訪問E節點的左子樹，沒找到，訪問E節點，然后訪問E節點的右子樹，沒找到，此時B結點的右子樹訪問完了。也是A節點的左子樹訪問完了

訪問A節點，然后訪問A節點的右子樹，找到了C節點，訪問C節點之前，要訪問C節點的左子樹，沒找到，訪問C節點，然后訪問C節點的右子樹，沒找到，此時A節點的右子樹訪問完畢。

結束遍歷.

NULL——D——NULL——B——NULL——E——NULL——A——NULL——C——NULL

DBEAC

中序的代碼實現：

// 二叉樹中序遍歷
void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->_left);// 訪問左子樹printf("%c ", root->_data); // 訪問根InOrder(root->_right);// 訪問右子樹
}

中序的調用思路如圖所示：

后序遍歷的順序是：左子樹——右子樹——根

遍歷思路是這樣的：

想要訪問A這個節點就要先訪問A節點的左子樹和右子樹，先訪問左子樹，找到了B節點，要訪問B節點就要先訪問B節點的左子樹，找到了D節點，要訪問D節點就要先訪問D節點的左子樹，沒找到，就訪問D節點的右子樹，沒找到，這個時候才訪問D節點。

這個時候B節點的左子樹訪問完了，訪問B節點的右子樹，找到了E節點，要訪問E節點，就要先訪問E節點的左子樹，沒找到，就訪問E節點的右子樹，沒找到，訪問E節點，這個時候B結點的左子樹和右子樹都訪問完了，也是A節點的左子樹訪問完了。

這個時候要訪問A節點的右子樹，找到了C節點，要訪問C節點，就要訪問C節點的左子樹和右子樹，訪問左子樹，沒找到，訪問右子樹，沒找到，這個時候訪問C節點，這個時候A節點的右子樹訪問完畢，訪問A節點.

結束遍歷。

NULL——NULL——D——NULL——NULL——E——B——NULL——NULL——C——A

DEBCA

后序的代碼實現：

// 二叉樹后序遍歷
void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->_left);// 訪問左子樹PostOrder(root->_right);// 訪問右子樹printf("%c ", root->_data);// 訪問根}

后序的調用思路和前面兩個是大同小異的，都是遞歸的運用。

總結：

這三個遍歷都是深度優先的遍歷

4.2.2層序遍歷

層序遍歷：除了先序遍歷、中序遍歷、后序遍歷外，還可以對二叉樹進行層序遍歷。設二叉樹的根節點所在層數為1，層序遍歷就是從所在二叉樹的根節點出發，首先訪問第一層的樹根節點，然后從左到右訪問第2層上的節點，接著是第三層的節點，以此類推，自上而下，自左至右逐層訪問樹的結點的過程就是層序遍歷。

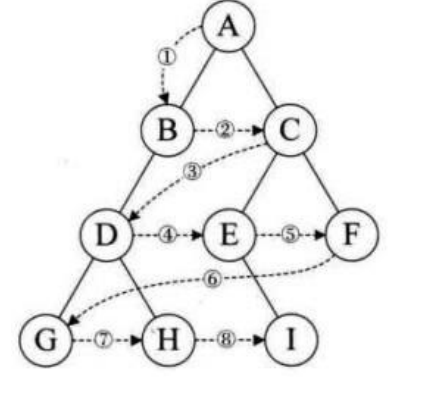
舉個例子：

如圖所示，如果是層序遍歷，那遍歷順序是：

A——B——C——D——E——F——G——NULL——NULL——NULL——H——NULL——NULL——NULL——NULL。

思路：（借助隊列）

1. 其實層序遍歷二叉樹，就不是用遞歸實現了，和之前的前序、中序、后序就沒有什么關系了
2. 層序遍歷需要借助隊列的先進先出的特性。將根結點放進去，根結點出來的時候，要把其左右孩子依次放入隊列。
3. 直至遍歷到隊列為空，此時二叉樹就遍歷完畢了

有關層序中借助的隊列的定義和實現：

Queue.h

#pragma once
#define  _CRT_SECURE_NO_WARNINGS 1
# include<stdio.h>
# include<assert.h>
# include<stdlib.h>// 這里的隊列的底層數據結構是單鏈表
// 定義節點的結構體#include"BinaryTree.h";typedef BTNode* QDataType; // 以二叉樹節點的指針作為數據存儲類型
typedef struct QueueNode
{QDataType _data;struct QueueNode* _next;
}QueueNode;// 和單鏈表不一樣的是隊列最好要有指向第一個節點和尾節點的指針
typedef struct Queue
{QueueNode* _head;QueueNode* _tail;
}Queue;// 隊列的接口（也就是函數） 
// 為什么這里的接口和單鏈表的時候不一樣，不需要傳二級指針呢，因為我們把指針放到了結構體內部，傳的是結構體指針
// 通過結構體指針找到結構體，再從結構體內部拿到節點的指針，再從這個節點指針找到節點，這里起到的作用就類似于二級指針// 隊列的初始化
void QueueInit(Queue* pq);// 隊列的銷毀
void QueueDestory(Queue* pq);// 入隊
void QueuePush(Queue* pq, QDataType x);// 出隊
void QueuePop(Queue* pq);// 獲取隊頭的數據
QDataType QueueFront(Queue* pq);// 獲取隊尾的數據
QDataType QueueBack(Queue* pq);// 判斷隊列是否為空  [返回1就是空，返回0就是非空]
int QueueEmpty(Queue* pq);// 獲取隊列的數據個數
int QueueSize(Queue* pq);

層序中用到的接口的代碼實現:

#include "Queue.h"// 隊列的初始化
void QueueInit(Queue* pq)
{assert(pq);//pq不能為NULL// 初始化pq->_head = NULL;pq->_tail = NULL;}// 隊列的銷毀
void QueueDestory(Queue* pq)
{assert(pq);// 遍歷隊列，刪除每一個節點QueueNode* cur = pq->_head;while (cur) {QueueNode* next = cur->_next;free(cur);cur = next;}pq->_head = pq->_tail = NULL;
}// 入隊
void QueuePush(Queue* pq, QDataType x)
{assert(pq);// 入隊其實就是讓新節點尾插到鏈表中QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));if (newnode == NULL){perror("QueuePush():malloc()");exit(-1);}newnode->_data = x;newnode->_next = NULL;// 判斷列隊是否為空if (pq->_head == NULL){pq->_head = pq->_tail = newnode;}else{// 尾插pq->_tail->_next = newnode;pq->_tail = newnode;}}// 出隊
void QueuePop(Queue* pq)
{assert(pq);assert(pq->_head); // 隊列是空的怎么出隊// 頭刪QueueNode* next = pq->_head->_next; // 把第一個節點的下一個節點存儲起來free(pq->_head);pq->_head = next;// 這里有個問題，當最后一個節點刪除完之后，pq->_head = NULL// 但是pq->_tail 就變成野指針了if (pq->_head == NULL){pq->_tail = NULL;}}// 獲取隊頭的數據
QDataType QueueFront(Queue* pq)
{assert(pq);assert(pq->_head);// 隊列為空怎么獲取隊頭數據return pq->_head->_data;
}// 獲取隊尾的數據
QDataType QueueBack(Queue* pq)
{assert(pq);assert(pq->_tail); // 等價于assert(pq->_head); 頭為空，尾也肯定為空，return pq->_tail->_data;
}// 判斷隊列是否為空 [返回1就是空，返回0就是非空]
int QueueEmpty(Queue* pq)
{assert(pq);return pq->_head == NULL ? 1 : 0;
}

層序的代碼實現：

// 層序遍歷(借助隊列)
void LevelOrder(BTNode* root)
{Queue q;QueueInit(&q);// 一開始根節點就是NULL就返回if (root == NULL)return;QueuePush(&q, root); //把根結點插入隊列中while (!QueueEmpty(&q)){// 獲取隊頭節點BTNode* frontnode = QueueFront(&q);QueuePop(&q); // 彈出隊頭printf("%c ", frontnode->_data);// 遍歷完隊頭節點，要把該節點的左右子樹依次插入隊列// 如果左右子節點是NULL 就不放進去 層序遍歷不打印NULLif (frontnode->_left) QueuePush(&q, frontnode->_left);if (frontnode->_right)QueuePush(&q, frontnode->_right);}printf("\n");// 銷毀隊列QueueDestory(&q);
}

測試代碼：

	// 層序遍歷(借助隊列)LevelOrder(A); // A B C D E

層序的遍歷是廣度優先的遍歷

學習了二叉樹的遍歷之后，我們可以來做幾個題來鞏固一下：

1.某完全二叉樹按層次輸出（同一層從左到右）的序列為 ABCDEFGH 。該完全二叉樹的前序序列為（ ）
A ABDHECFG
B ABCDEFGH
C HDBEAFCG
D HDEBFGCA2.二叉樹的先序遍歷和中序遍歷如下：先序遍歷：EFHIGJK;中序遍歷：HFIEJKG.則二叉樹根結點為（）
A E
B F
C G
D H3.設一課二叉樹的中序遍歷序列：badce，后序遍歷序列：bdeca，則二叉樹前序遍歷序列為____。
A adbce
B decab
C debac
D abcde4.某二叉樹的后序遍歷序列與中序遍歷序列相同，均為 ABCDEF ，則按層次輸出（同一層從左到右）的序列
為
A FEDCBA 
B CBAFED
C DEFCBA
D ABCDEF

答案是： A A D A 

4.3二叉樹的節點個數

這里需要注意，由于我們是通過遞歸來實現的，因此之前的常規思路是不能實現的。

常規思路代碼如下：

// 二叉樹節點個數
int BinaryTreeSize(BTNode* root)
{if (root == NULL)return 0;int size = 0;size++;BinaryTreeSize(root->_left);BinaryTreeSize(root->_right);return size;
}

測試代碼如下：

	// 獲取二叉樹節點個數printf("%d\n", BinaryTreeSize(A)); // 1printf("%d\n", BinaryTreeSize(A)); // 1

因為每遞歸一次都會重新定義一次size，因此每次++加的都不是同一個size，是不同層數的遞歸函數內重新定義的size

因此要實現這個思路，我們需要定義一個全局變量。

代碼如下：

// 二叉樹節點個數
int size = 0;
int BinaryTreeSize(BTNode* root)
{if (root == NULL)return 0;size++;BinaryTreeSize(root->_left);BinaryTreeSize(root->_right);return size;
}

測試代碼：

	// 獲取二叉樹節點個數printf("%d\n", BinaryTreeSize(A)); // 5printf("%d\n", BinaryTreeSize(A)); // 10

雖然這樣確實是可以統計出二叉樹的節點個數，但是由于是全局變量，我們會發現，調用完一次之后，不會消失，而是會累加，這樣除非我們手動再去重置，不然再調用該函數就會出錯。這樣也不好。

既然如此，我們可以考慮指針的方式，傳一個int 類型的指針，讓其在函數內部不斷改變，因為不是全局變量，調用完一次函數也會銷毀。

代碼如下：

// 二叉樹節點個數
void BinaryTreeSize(BTNode* root, int* psize)
{if (root == NULL)return 0;else(*psize)++;BinaryTreeSize(root->_left, psize);BinaryTreeSize(root->_right, psize);}

測試代碼：

	// 獲取二叉樹節點個數int sizeA = 0;BinaryTreeSize(A, &sizeA);printf("%d\n", sizeA); // 5printf("%d\n", sizeA); // 5

這樣確實可以解決問題，但是這樣調用不方便呀。我們都覺得調用這個函數接口，你應該直接給我返回這個二叉樹的節點個數，怎么還需要我去定義一個變量去使用呢？

因此我們用下面這個代碼的思路，可以直接返回二叉樹節點的個數。

• 二叉樹的節點個數 = 根節點 + 左子樹的節點個數 + 右子樹的節點個數

代碼如下：

// 二叉樹節點個數
int BinaryTreeSize(BTNode* root)
{	// 先看看是不是空樹，并且判斷root是否遍歷到了NULLif (root == NULL)return 0;// 二叉樹的節點個數 = 根節點 + 左子樹的節點個數 + 右子樹的節點個數elsereturn 1 + BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right);
}

測試代碼：

	// 獲取二叉樹節點個數printf("%d\n", BinaryTreeSize(A)); // 5printf("%d\n", BinaryTreeSize(A)); // 5printf("%d\n", BinaryTreeSize(B)); // 3

4.4二叉樹葉子節點個數

關于這個葉子節點個數的獲取，我們還是要通過遞歸的思想。

• 一個二叉樹的葉子節點的個數 = 左子樹的葉子節點個數 + 右子樹的葉子節點個數

代碼如下：

// 二叉樹葉子節點個數
int BinaryTreeLeafSize(BTNode* root)
{// 先判斷是否是空樹if (root == NULL)return 0;// 判斷root是否是葉子結點，如果是，那么左右子樹都是NULLif (root->_left == NULL && root->_right == NULL)return 1;// 一個根節點的葉子節點的個數相當于 左子樹的葉子節點個數 + 右子樹的葉子節點個數return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}

測試代碼如下：

	// 獲取二叉樹葉子節點個數 printf("%d\n", BinaryTreeLeafSize(A)); // 3printf("%d\n", BinaryTreeLeafSize(B)); // 2

4.5二叉樹的深度

思路：

• 求出左子樹的深度和右子樹的深度，判斷誰大， 大的就 + 1

代碼如下：

// 獲取二叉樹的深度
int BinaryTreeDepth(BTNode* root)
{if (root == NULL)return 0;// 求出左子樹 右子樹 的深度int leftdepth = BinaryTreeDepth(root->_left);int rightdepth = BinaryTreeDepth(root->_right);// 判斷誰大，誰大就 + 1return leftdepth > rightdepth ? leftdepth + 1 : rightdepth + 1;
}

測試代碼：

	// 獲取二叉樹最大深度printf("BinaryTreeDepthA:%d\n", BinaryTreeDepth(A)); // 3printf("BinaryTreeDepthB:%d\n", BinaryTreeDepth(B)); // 3

4.6二叉樹第K層節點個數

思路：

當前樹的第k層 可以轉化成左右子樹的第k - 1層， 當層數 == 1的時候，就不分解，返回1。

代表這里有一個節點，如果是NULL 就返回0.

代碼：

// 二叉樹第k層節點個數
int BinaryTreeLevelKSize(BTNode* root, int k)
{// 如果傳進來的根節點是NULL 直接返回0 代表沒有節點if (root == NULL)return 0;// 判斷是否分離到最后一層if (k == 1)return 1;// 當前樹的第k層 可以轉化成左右子樹的第k - 1層// 第k層的節點個數 就是第k-1層的左右子節點個數,那我們就統計 k - 1層的左右子節點個數 // k = 1 的時候就說明此時層數 就是第k - 1層的左右子節點的層數 也就是我們要求的第k層return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);
}

測試代碼：

	// 獲取二叉樹第k層節點個數printf("BinaryTreeLevelKSize2:%d\n", BinaryTreeLevelKSize(A, 2)); // 2printf("BinaryTreeLevelKSize3:%d\n", BinaryTreeLevelKSize(A, 3)); // 2

4.7二叉樹查找值為x的節點

思路：

• 遍歷二叉樹，查找x是否存在x的節點就行，有就返回該節點，沒有返回NULL

代碼：

// 二叉樹查找值為x的節點
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;// 前序遍歷二叉樹if (root->_data == x)return root;// 如果根結點沒找到，就去左子樹找BTNode* node = BinaryTreeFind(root->_left, x);if (node)// node沒找到就是NULL  找到了就不是NULLreturn node;// 左子樹也沒找到就去右子樹找node = BinaryTreeFind(root->_right, x);if (node)return node;// 走到這里就說明沒找到return NULL;
}

測試代碼：

	// 二叉樹查找值為x的節點BTNode* node = BinaryTreeFind(A, 'C');if (node)printf("BinaryTreeFind:%c\n", node->_data);// BinaryTreeFind:Celseprintf("NULL\n");

4.8二叉樹基礎oj練習

1. 單值二叉樹。單值二叉樹

2. 檢查兩顆樹是否相同。相同的樹

3. 對稱二叉樹。對稱二叉樹

4. 二叉樹的前序遍歷。 二叉樹的前序遍歷

5. 二叉樹中序遍歷 。二叉樹的中序遍歷

6. 二叉樹的后序遍歷 。二叉樹的后序遍歷

7. 另一顆樹的子樹。另一棵樹的子樹

具體解析看另外一篇博客，鏈接：

二叉樹基礎oj練習【11道題】-CSDN博客

4.9二叉樹的創建與銷毀

4.9.1二叉樹的創建

二叉樹構建和遍歷

這道leetcode的題可以當做參考

思路：

1. 判斷傳進來的數組元素是否是# 也就是是否為空
2. 如果不為空，通過前序遍歷構建出這個二叉樹

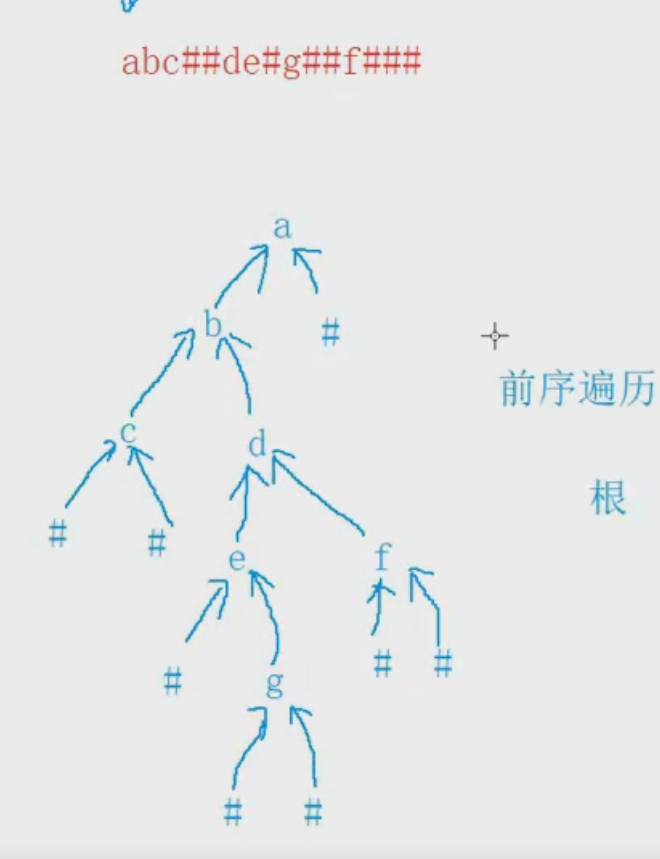
代碼：

// 通過前序遍歷的數組"ABD##E#H##CF##G##"構建二叉樹
BTNode* BinaryTreeCreate(BTDataType* a, int* pi)
{// 判斷傳進來的數組元素是否是# 也就是是否是空if (a[(*pi)] == '#'){(*pi)++;return NULL;}else{// 如果不是空 那就要前序構建二叉樹  BTNode* root = (BTNode*)malloc(sizeof(BTNode)); // 構建節點root->_data = a[(*pi)];(*pi)++;// 前序構建二叉樹root->_left = BinaryTreeCreate(a, pi);root->_right = BinaryTreeCreate(a, pi);return root;}
}

測試代碼：

	// 通過前序遍歷的數組"ABD##E#H##CF##G##"構建二叉樹char str[100] = "ABD##E#H##CF##G##";int i = 0;BTNode* root = BinaryTreeCreate(str, &i);PreOrder(root); // A B D NULL NULL E NULL H NULL NULL C F NULL NULL G NULL NULLprintf("\n");

4.9.2二叉樹的銷毀

比較簡單，直接看代碼：

// 二叉樹銷毀
void BinaryTreeDestory(BTNode* root) // 也可以使用二級指針，為了接口一致性也可以用一級指針，看需求
{if (root == NULL)return;// 采用后序銷毀二叉樹，前序銷毀要注意能否找到下一子節點的問題BinaryTreeDestory(root->_left);BinaryTreeDestory(root->_right);free(root);
}

4.10判斷二叉樹是否為完全二叉樹

思路：

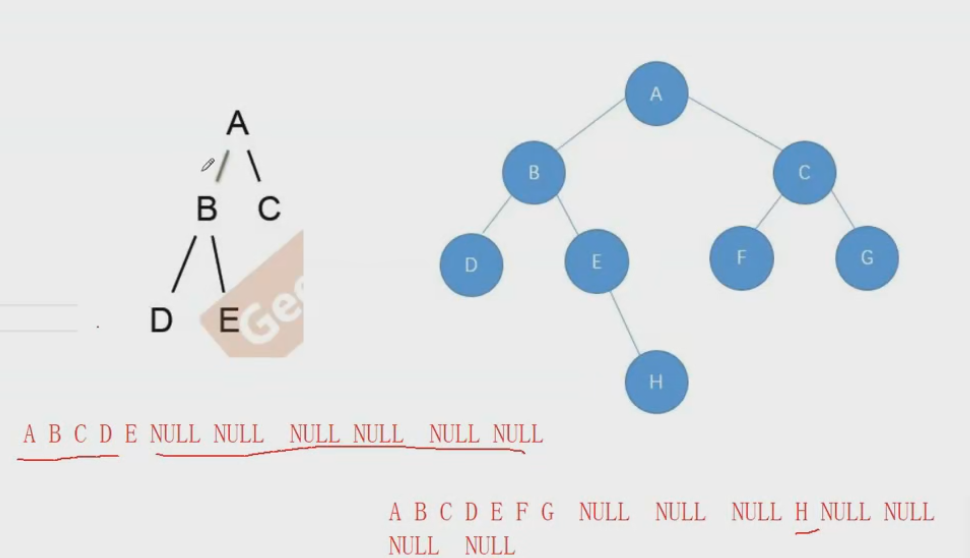
如圖所示

• 如果我們層序遍歷一個二叉樹，如果這個二叉樹是完全二叉樹，那么最終打印的結構，二叉樹的值和 NULL 是氛圍兩個階段的
• 但是如果不是完全二叉樹，那么NULL 和 值 就不是兩段了。

因此我們可以利用這個特性來判斷二叉樹是否為完全二叉樹

代碼：

// 判斷二叉樹是否是完全二叉樹 （是就返回1 不是就返回0）
int BinaryTreeComplete(BTNode* root)
{// 先層序二叉樹，根據層序的結果來判斷是否是完全二叉樹Queue q;QueueInit(&q); // 初始化// 判斷一開始的根結點是否是NULLif (root == NULL){QueueDestory(&q);return 1; // 我們認為空樹也是完全二叉樹}// 層序二叉樹 (這里的層序需要NULL進入隊列)QueuePush(&q, root);while (!QueueEmpty(&q)){// 獲取隊頭BTNode* frontnode = QueueFront(&q);QueuePop(&q); // 彈出隊頭// 訪問隊頭的數據if (frontnode == NULL) // 如果是空就判斷隊列中剩下的數據是否都是NULLbreak; // 跳出循環// 訪問完之后要把該節點的左右子節點依次插入到隊列當中QueuePush(&q, frontnode->_left);QueuePush(&q, frontnode->_right);}// 走到這里就判斷隊列中剩下的數據是否都是NULL// 因為如果是完全二叉樹的層序，層序到NULL 就說明所有節點都層序完了// 如果都是NULL 就是完全二叉樹while (!QueueEmpty(&q)) // 遍歷隊列中剩下的數據{BTNode* Frontnode = QueueFront(&q); // 獲取隊頭QueuePop(&q); // 彈出隊頭// 判斷隊頭是否是NULLif (Frontnode != NULL){QueueDestory(&q);// 銷毀隊列return 0; // 只要不是NULL就不是完全二叉樹}}// 走到這里說明 隊列中剩下的數據都是NULL// 那就是完全二叉樹QueueDestory(&q);// 銷毀隊列return 1;
}

5.總結

有關二叉樹的學習，目前已經學習了大概2/5的樣子，后面更加有難度的，比如搜索平衡二叉樹，紅黑樹等知識，將在C++學習