目錄

1. 比較排序和非比較排序

2. 計數排序的原理

2.1 計數排序的弊端

3.代碼復現

3.1 代碼分析

3.2 排序核心

3.3 時間、空間復雜度

---

1. 比較排序和非比較排序

? ? ? ? 比較排序是根據排序元素的具體數值比較來進行排序；非比較排序則相反，非比較排序例如：基數排序和計數排序，這兩種排序方式雖然諧音類似，但是其實是完全不同的兩種排序。

????????首先基數排序是根據一個數字的某一位進行排序；而計數排序是根據某一個數字出現的次數來進行比較排序。

2. 計數排序的原理

①需要判斷出整個原數組中最大的數字，例如是5，那么就需要創建一個0-5的數組（元素為6個）。

②新創建的數組的下標表示該數字的值，該數組的下標所對應的值就類似于該數字出現了幾次。

③遍歷原始數組，如果遍歷到某一個數字，那么新數組的對應位置的值就會+1；

④遍歷完畢之后，對統計次數的數組進行排序即可；

⑤排序的過程也非常巧妙，首先0下標的值是2，說明0出現了2次，1下標的值是0，說明沒有1,2下標的值是2說明有兩個2......我們直接對原數組進行覆蓋即可。

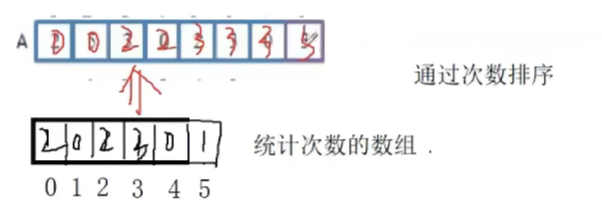
2.1 計數排序的弊端

????????例如需要將下面幾個數進行計數排序，按照上面的原理，我們需要開辟一個0-5000（5001個數組元素）的數組，但是需要排序的數只有僅僅5個，這樣一來，大量的數組空間會被浪費。

? ? ? ? 從下圖得知，最小的數是1000，也就是說0-1000這1000個數就沒有必要為其準備空間了，所以只需要準備4000個空間就夠了。

????????此時數的存儲是一個相對位置，例如1000存在數組下標為0的位置上，1005存在數組下標為5的位置上，1100存儲在數組下標為100的位置上......5000存在數組下標為4000，計算方式a[i] - min，當前位置-最小值。

? ? ? ? 所以說，比較稀疏的數進行排序的話，那么就會浪費大量連續空間。

3.代碼復現

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<string.h>
#include<stdlib.h>// 計數排序
void count_sort(int* arr, int size)
{// 選出最大值和最小值int max = arr[0];int min = arr[0];for (int i = 0; i < size; i++){if (arr[i] > max){max = arr[i];}if (arr[i] < min){min = arr[i];}}// 創建一個具體數量的數組int range = max - min + 1;// 0-9一共10個數int* countArr = (int*)malloc(sizeof(int) * range);memset(countArr, 0, range * sizeof(int));// 遍歷原數組給countArr賦值,計數for (int i = 0; i < size; i++)// countArr下標是arr的值;其值是次數{int val = arr[i] - min; // 這里是相對位置，若只有0-4000個位置，1005就是5號位置,// 這里要arr[i] - min得到相對位置++countArr[val];}int index = 0;// 原數組的覆蓋下標// 遍歷countArr將原數組覆蓋for (int j = 0; j < range; j++){// 計數數組的值是幾就覆蓋幾次while (countArr[j]--){arr[index++] = j + min; // 將下標進行還原，之前是-min存入countArr的 }}free(countArr);
}int main()
{int a[] = { 3,5,4,1,7,9,8,5,0,5 };int size = sizeof(a) / sizeof(int);count_sort(a, size);for (int i = 0; i < size; i++){printf("%d ", a[i]);}return 0;
}

3.1 代碼分析

①首先計算出原數組的最大最小值，最大值-最小值+1就是計數數組的長度。

②遍歷原數組，原數組的值對應計數數組的下標，如果遍歷到2，那么就是計數數組下標為2的值進行+1；

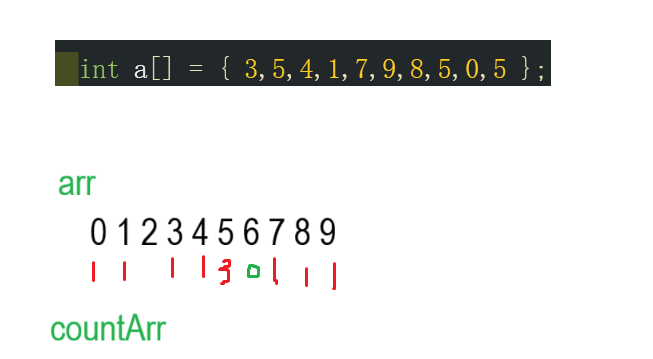
③遍歷計數數組，將對應下標作為原數組的值，計數數組的值就是需要賦值的次數，例如上圖的5，在計數數組中存儲的方式是index = 5,val = 3，那么就是將5賦值原數組，賦值3次，結果如下圖。

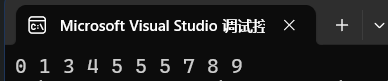
3.2 排序核心

? ? ? ? 就是利用數組的下標將無序的數字分別放入對應的下標，從而實現有序，這里對于重復數字進行一個累加的過程，反作用于原數組就是賦值的次數，這樣的排序類似于下圖：

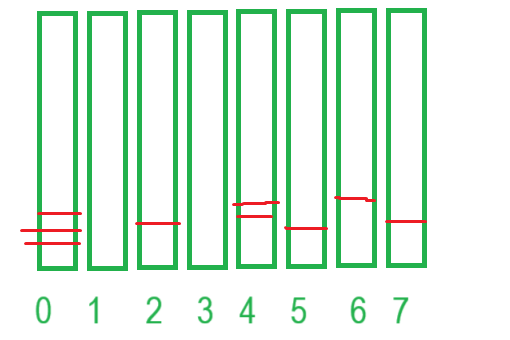
? ? ? ? 利用連續的有序數組下標作為“柱子”，如果該數字為這個柱子的編號，那么這個柱子就套一個圈，每一個柱子套圈的個數其實就是該數字出現的次數，由于柱子的編號是連續且有序，其實在套圈的過程中，我們已經將數字排好序了，此時只需要將結果覆蓋原數組即可。

? ? ? ? 所以這個算法可以運用于，數據非常集中，有大量重復出現的數字的數組中。

3.3 時間、空間復雜度

? ? ? ? 我們注意這里的時間復雜度，看代碼我們可以發現遍歷了一次原數組，這里時間復雜度是O(n)，后面需要遍歷計數數組，那么時間復雜度是O（range）,那么最后的時間復雜度就是：

空間復雜度，這里只需要一個range大的數組，所以這里是：

(不是橘子哈)