C++---雙指針

在C++編程中，雙指針算法是一種高效的解題思路，其核心是通過設置兩個指針（或索引）遍歷數據結構（如數組、鏈表、字符串等），利用指針的移動規則減少無效操作，從而將時間復雜度從暴力解法的O(n2)優化至O(n)或O(n log n)。這種算法廣泛應用于鏈表操作、數組處理、字符串匹配等場景。

一、雙指針算法的核心思想

雙指針算法的本質是通過兩個指針的協同移動，縮小問題的處理范圍。與暴力解法中嵌套循環的“盲目遍歷”不同，雙指針的移動具有明確的邏輯（如基于數據的有序性、結構特性等），從而避免冗余計算。

其核心優勢體現在：

時間優化：將多層循環轉化為單層遍歷，降低時間復雜度；
空間優化：多數情況下無需額外空間（原地操作），空間復雜度可保持O(1)；
邏輯清晰：通過指針的移動規則直觀反映問題的解決思路。

二、雙指針的常見類型及應用場景

根據指針的移動方向和作用，雙指針可分為三大類：快慢指針、左右指針、同向指針。以下結合具體場景詳細講解。

（一）快慢指針（Floyd’s Tortoise and Hare）

快慢指針指兩個指針以不同速度遍歷數據結構（如鏈表中，快指針每次走2步，慢指針每次走1步）。其核心應用是處理鏈表中的環問題和查找特定位置（如中間節點）。

1. 鏈表環檢測（LeetCode 141）

問題：判斷一個單鏈表是否存在環。
暴力解法：用哈希表記錄訪問過的節點，若重復訪問則有環，時間O(n)但空間O(n)。
雙指針解法：

設快指針fast和慢指針slow，初始均指向頭節點；
fast每次移動2步，slow每次移動1步；
若鏈表有環，fast會先進入環并繞環移動，最終與slow在環內相遇；
若fast到達nullptr，則無環。

代碼實現：

struct ListNode {int val;ListNode *next;ListNode(int x) : val(x), next(nullptr) {}
};bool hasCycle(ListNode *head) {if (head == nullptr || head->next == nullptr) return false;ListNode *slow = head;ListNode *fast = head->next; // 初始錯開，避免直接相遇while (slow != fast) {if (fast == nullptr || fast->next == nullptr) return false;slow = slow->next;       // 慢指針走1步fast = fast->next->next; // 快指針走2步}return true;
}

時間復雜度：O(n)（無環時fast走n/2步；有環時相遇前slow最多走n步）。
空間復雜度：O(1)（僅用兩個指針）。

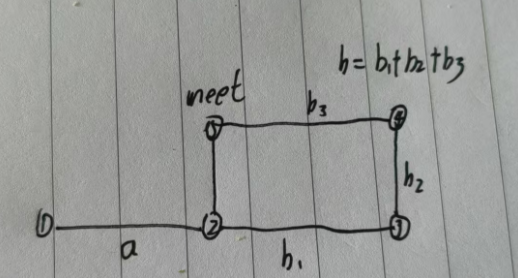
2. 尋找環的入口（LeetCode 142）

問題：若鏈表有環，找到環的入口節點。
算法思路：

先用快慢指針判斷有環，記錄相遇點meet；
讓slow從頭節點出發，fast從meet出發，兩者均每次走1步；
兩指針再次相遇的節點即為環的入口。

原理：設頭節點到入口距離為a，入口到相遇點距離為b，環長為c。則相遇時：

slow走了a + b；
fast走了a + b + k*c（繞環k圈）；
因fast速度是slow的2倍，故2*(a + b) = a + b + k*c → a = k*c - b b=k*c-a。
因此，slow從頭部走a步，與fast從meet走k*c - b步（等價于繞環k圈后回到入口）相遇。

重置slow = 0,fast仍在meet處（等價于初始走了a+b），當slow=a(slow走了a步)，fast=a+b+kc-b=a+kc，所以a,b在環的入口相遇

代碼實現：

ListNode *detectCycle(ListNode *head) {if (head == nullptr) return nullptr;ListNode *slow = head, *fast = head;// 第一步：找到相遇點do {if (fast->next == nullptr || fast->next->next == nullptr) return nullptr;slow = slow->next;fast = fast->next->next;} while (slow != fast);// 第二步：尋找入口slow = head;while (slow != fast) {slow = slow->next;fast = fast->next;}return fast;
}

3. 尋找鏈表的中間節點（LeetCode 876）

問題：返回單鏈表的中間節點（若長度為偶數，返回第二個中間節點）。
算法思路：

快指針每次走2步，慢指針每次走1步；
當fast到達尾節點時，slow恰好指向中間節點。

代碼實現：

ListNode* middleNode(ListNode* head) {ListNode *slow = head, *fast = head;while (fast != nullptr && fast->next != nullptr) {slow = slow->next;fast = fast->next->next;}return slow;
}

（二）左右指針（相向指針）

左右指針指兩個指針分別從數據結構的兩端出發，相向而行（左指針從左向右，右指針從右向左），多用于有序數組/字符串的處理。其核心是利用數據的有序性，通過指針移動排除無效解。

1. 兩數之和（有序數組版，LeetCode 167）

問題：給定有序數組nums和目標值target，找到兩個數使得和為target，返回索引（下標從1開始）。
暴力解法：嵌套循環遍歷所有組合，時間O(n2)。
雙指針解法：

左指針left初始指向0，右指針right指向n-1；
計算當前和sum = nums[left] + nums[right]：
- 若sum == target，返回[left+1, right+1]；
- 若sum > target，說明右指針太大，right--；
- 若sum < target，說明左指針太小，left++。

原理：數組有序保證了指針移動的有效性——當sum > target時，減小右指針可降低總和；當sum < target時，增大左指針可提高總和，無需檢查其他組合。

代碼實現：

vector<int> twoSum(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;while (left < right) {int sum = nums[left] + nums[right];if (sum == target) {return {left + 1, right + 1};} else if (sum > target) {right--;} else {left++;}}return {-1, -1}; // 題目保證有解，此行為冗余
}

時間復雜度：O(n)，空間復雜度O(1)。

2. 反轉字符串（LeetCode 344）

問題：原地反轉字符串（如["h","e","l","l","o"]→["o","l","l","e","h"]）。
算法思路：

左指針left指向0，右指針right指向n-1；
交換nums[left]與nums[right]，然后left++、right--，直到left >= right。

代碼實現：

void reverseString(vector<char>& s) {int left = 0, right = s.size() - 1;while (left < right) {swap(s[left], s[right]);left++;right--;}
}

3. 二分查找（本質是左右指針的變體）

二分查找中，left和right指針分別指向搜索范圍的兩端，通過比較中間值與目標值，不斷縮小范圍，本質是左右指針的“跳躍式移動”。

代碼實現：

int search(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;while (left <= right) {int mid = left + (right - left) / 2; // 避免溢出if (nums[mid] == target) return mid;else if (nums[mid] < target) left = mid + 1;else right = mid - 1;}return -1;
}

（三）同向指針（一前一后指針）

同向指針指兩個指針從同一端出發，沿相同方向移動（通常一個在前“探索”，一個在后“記錄”），多用于數組去重、子數組/子串問題。

1. 刪除有序數組中的重復項（LeetCode 26）

問題：原地刪除有序數組中的重復元素，返回新長度（如[1,1,2]→長度2，數組變為[1,2]）。
算法思路：

慢指針slow記錄有效元素的尾位置（初始0）；
快指針fast遍歷數組（初始1）；
若nums[fast] != nums[slow]，說明找到新元素，slow++并將nums[fast]復制到nums[slow]；
最終slow + 1為新長度。

代碼實現：

int removeDuplicates(vector<int>& nums) {if (nums.empty()) return 0;int slow = 0;for (int fast = 1; fast < nums.size(); fast++) {if (nums[fast] != nums[slow]) {slow++;nums[slow] = nums[fast];}}return slow + 1;
}

2. 移動零（LeetCode 283）

問題：將數組中的0移到末尾，保持非零元素的相對順序（如[0,1,0,3,12]→[1,3,12,0,0]）。
算法思路：

慢指針slow記錄非零元素的尾位置（初始0）；
快指針fast遍歷數組，若nums[fast] != 0，則交換nums[slow]與nums[fast]，slow++；
遍歷結束后，slow及之后的位置全部賦0。

代碼實現：

void moveZeroes(vector<int>& nums) {int slow = 0;for (int fast = 0; fast < nums.size(); fast++) {if (nums[fast] != 0) {swap(nums[slow], nums[fast]);slow++;}}// 剩余位置補0（可選，因原數組0已被交換到后面）for (int i = slow; i < nums.size(); i++) {nums[i] = 0;}
}

3. 滑動窗口（同向指針的高級應用）

滑動窗口是同向指針的典型場景，用于解決子數組/子串的最值問題（如最長、最短、包含特定元素等）。其核心是用left和right指針維護一個“窗口”，通過移動right擴張窗口，移動left收縮窗口，在O(n)時間內找到最優解。

示例：長度最小的子數組（LeetCode 209）
問題：給定數組nums和目標值s，找到和≥s的最短子數組長度（若無則返回0）。

算法思路：

left和right初始均為0，sum記錄窗口內元素和；
移動right，將nums[right]加入sum；
當sum ≥ s時，嘗試移動left縮小窗口，更新最小長度；
重復直至right遍歷結束。

代碼實現：

int minSubArrayLen(int s, vector<int>& nums) {int n = nums.size();int min_len = INT_MAX;int left = 0, sum = 0;for (int right = 0; right < n; right++) {sum += nums[right];// 收縮窗口while (sum >= s) {min_len = min(min_len, right - left + 1);sum -= nums[left];left++;}}return min_len == INT_MAX ? 0 : min_len;
}