目錄

1. 整數在內存中的存儲

2. 大小端字節序

2.1 什么是大小端？

2.2 為什么有大小端？

2.3 練習

2.3.1 練習1

2.3.2 練習2

2.3.3 練習3

2.3.4 練習4

2.3.5 練習5

2.3.6 練習6

3. 浮點數在內存中的存儲

3.1?浮點數存儲的過程

3.2?浮點數的取出過程

---

1. 整數在內存中的存儲

在操作符的那一章的時候，我們就學習了一下內容，不清楚的小伙伴可以返回去看看。

整數的2進制表示方法有三種：原碼、反碼、補碼。

有符號整數，三種表示方法都有符號位和數值位兩部分，符號位0表示正，1表示負，最高位表示符號位，其他的表示數值位。

正整數原碼、反碼、補碼都是相同的。負整數則是各不相同。

其規則為：原碼：將數值按照正負數的形式翻譯為2進制得到的就是原碼。

反碼：原碼的符號位不變，其他位按位取反就可以得到反碼。

補碼：反碼+1得到的就是補碼。

對于整型來說，數據存放在內存中存放的是二進制的補碼。

2. 大小端字節序

我們之前在調試過程中，在查看內存情況時，會有疑惑為啥它是倒著儲存的，其實這里面有它自己的規則。

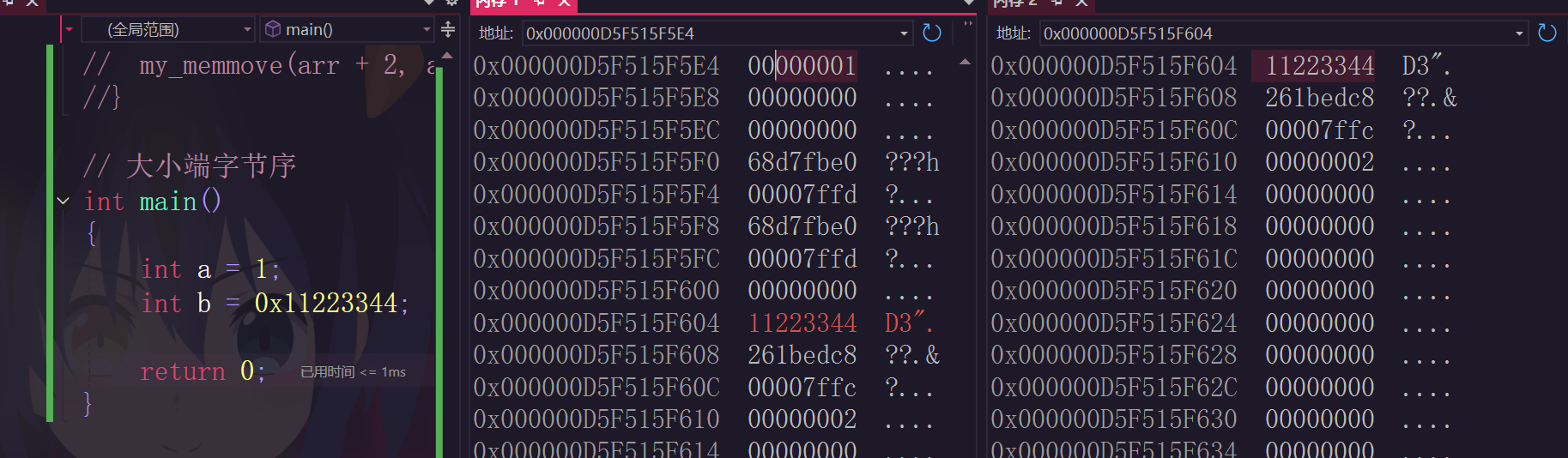
其實沒必要大驚小怪，有的是正著排的，有的是倒著排的。這就有關于大小端字節序的判斷了。

2.1 什么是大小端？

其實超過一個字節的數據在內存中存儲的時候，就有存儲順序的問題，按照不同的存儲順序，我們分為大端字節存儲和小端字節存儲，下面是具體概念：

大端存儲模式： 是指數據的低位字節內容保存在內存的高地址處。而數據的高位字節內容，保存在內存的低地址處。

小端存儲模式： 是指數據的低位字節內容保存在內存的低地址處，而數據的高位字節內容，保存在內存的高地址處。

這里是要記住的，方便進行區分。

2.2 為什么有大小端？

那么為什么會有大小端之分呢？直接正著存不是更方便嗎？

這是因為在計算機系統中，我們是以字節為單位的，每個地址單元都對應著一個字節，一個字節8個bit位，但是在C語言中除了8bit的char之外，還有16bit的short型，32bit的long型（具體要看編譯器），另外，對于位數大于8位的處理器，由于寄存器寬度大于1個字節，那么必然存在著一個如何將多個字節安排的問題，因此就導致了大端字節存儲模式和小端存儲模式。

2.3 練習

2.3.1 練習1

簡述大小端的概念，并設計一個程序檢測當前機器是什么模式。

答：大端：低位字節內容存放在高地址處，高位字節內容存放在低地址處。

小端：低位字節內容存放在低地址處，高位字節內容放在高地址處。

int check_sys()
{int i = 1;return ((char*)&i);
}
int main()
{if (check_sys() == 0)printf("大端\n");elseprintf("小端\n");
}

2.3.2 練習2

int main()
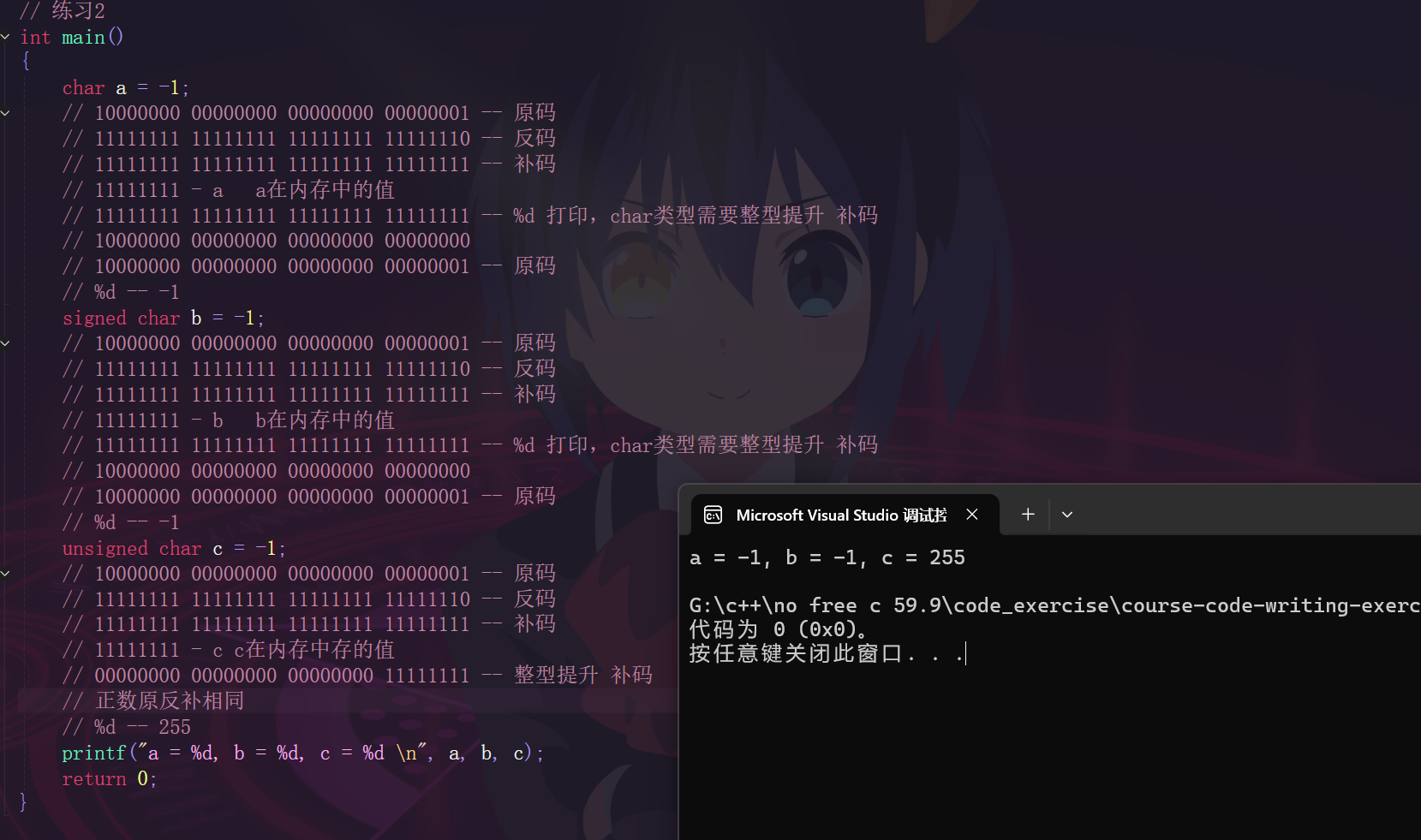
{char a = -1;signed char b = -1;unsigned char c = -1;printf("a = %d, b = %d, c = %d \n", a, b, c);return 0;
}

我們來看看這段代碼會打印什么值？

在計算這段代碼之前，我們先了解一下相關知識。

---

char ：-128~127

signed char ：-128~127

unsigned char：0~255?

這些范圍是怎么產生的？為什么就是這個范圍，請看下圖：

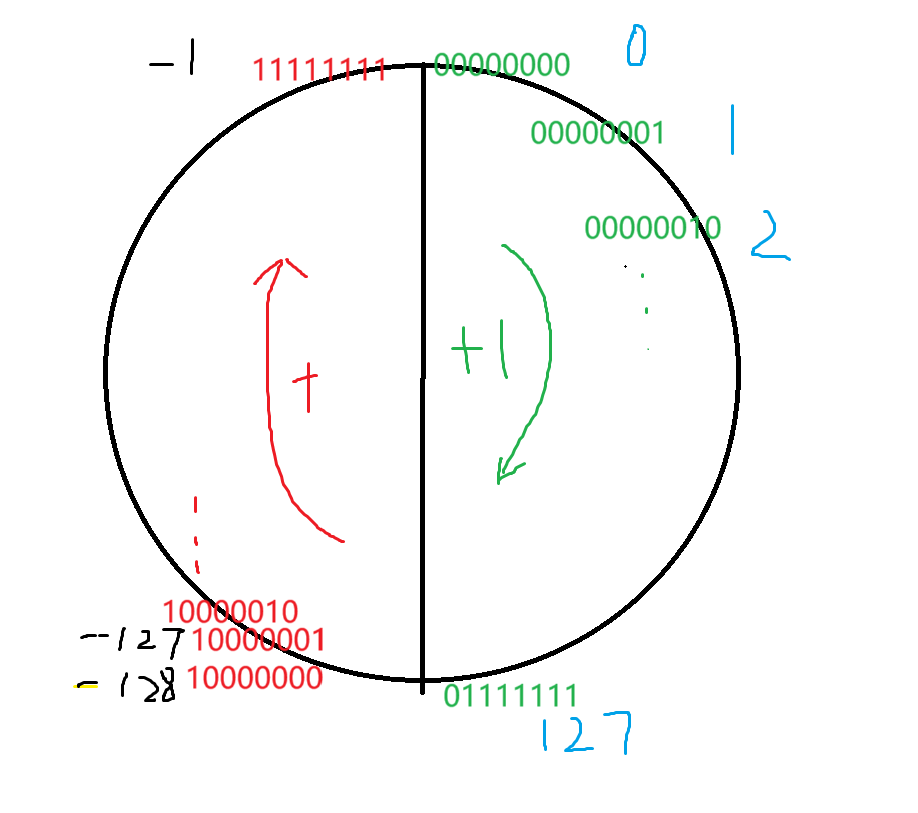
這是char的，short、int這些類型都可以以此類推。有了這些知識，我們來解答這道題。

2.3.3 練習3

int main()
{char a = -128;printf("%u\n", a);return 0;
}

%u -- 打印的是無符號整型

int main()
{char a = -128;// 10000000 00000000 00000000 10000000// 11111111 11111111 11111111 01111111// 11111111 11111111 11111111 10000000// 10000000 - a// 11111111 11111111 11111111 10000000// 4294967168printf("%u\n", a);return 0;
}

2.3.4 練習4

int main()
{char a[1000];int i = 0;for (i = 0; i < 1000; i++){a[i] = -1 - i;}printf("%d\n", strlen(a));return 0;
}

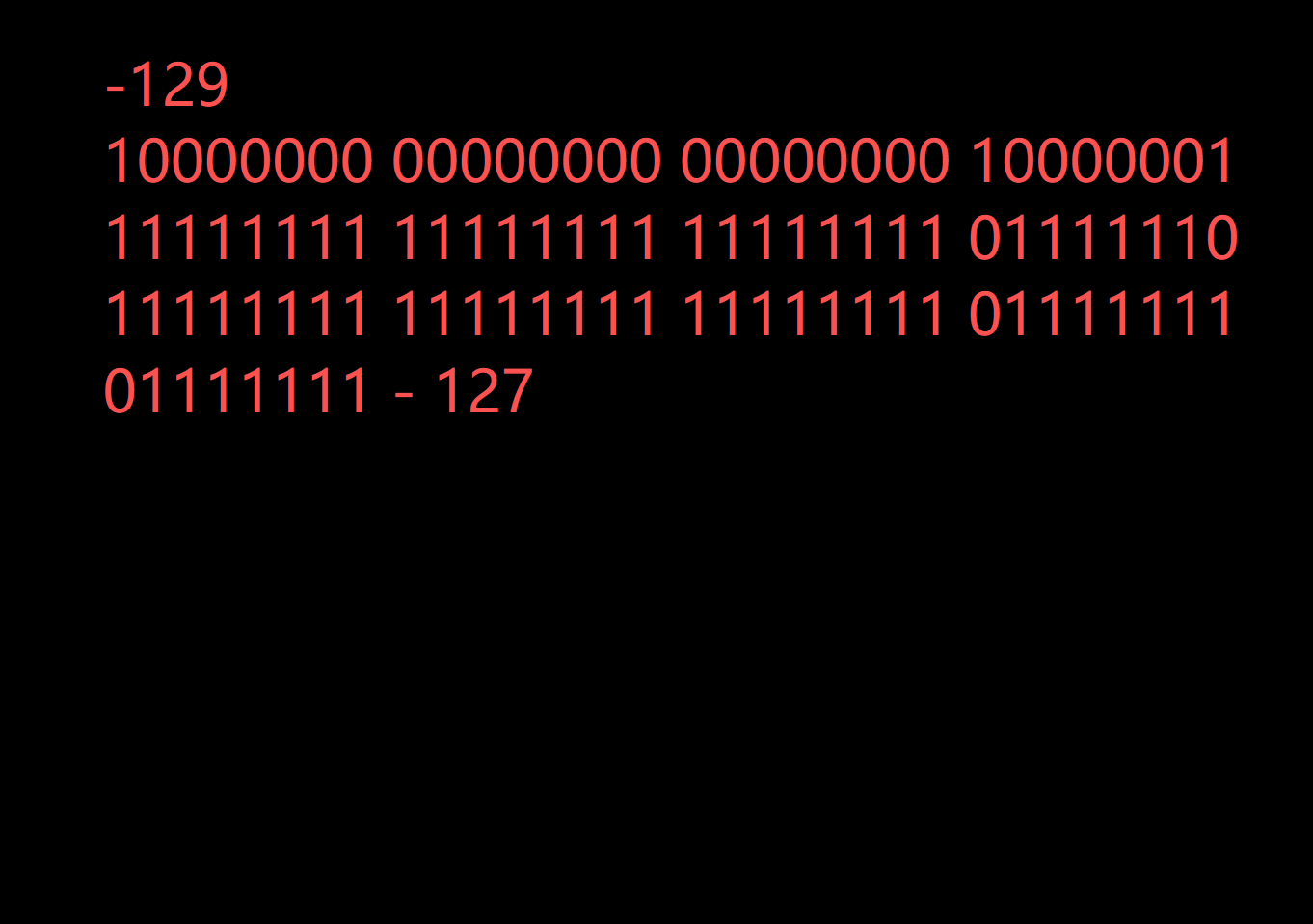
不難看出，他直接就是-128~127，也就是255.

2.3.5 練習5

int main()
{unsigned char i = 0;for (i = 0; i <= 255; i++){printf("hello world\n");}return 0;
}

代碼死循環了，因為i<=255這個條件是恒成立的。

2.3.6 練習6

int main()
{int a[4] = { 1,2,3,4 };int* ptr1 = (int*)(&a + 1);int* ptr2 = (int*)((int)a + 1);printf("%x, %x", ptr1[-1], *ptr2);return 0;
}

解題過程：

所以答案是4,2000000 小伙伴們答對了嗎？

3. 浮點數在內存中的存儲

浮點數有很多，比如說3.14159，1E10等。

我們先來看個例子：

int main()
{int n = 9;float* pFloat = (float*)&n;printf("n的值為：%d\n", n);printf("pFloat的值為：%f\n", *pFloat);*pFloat = 9.0;printf("n的值為：%d\n", n);printf("pF的值為：%f\n", *pFloat);return 0;
}

輸出是什么呢？

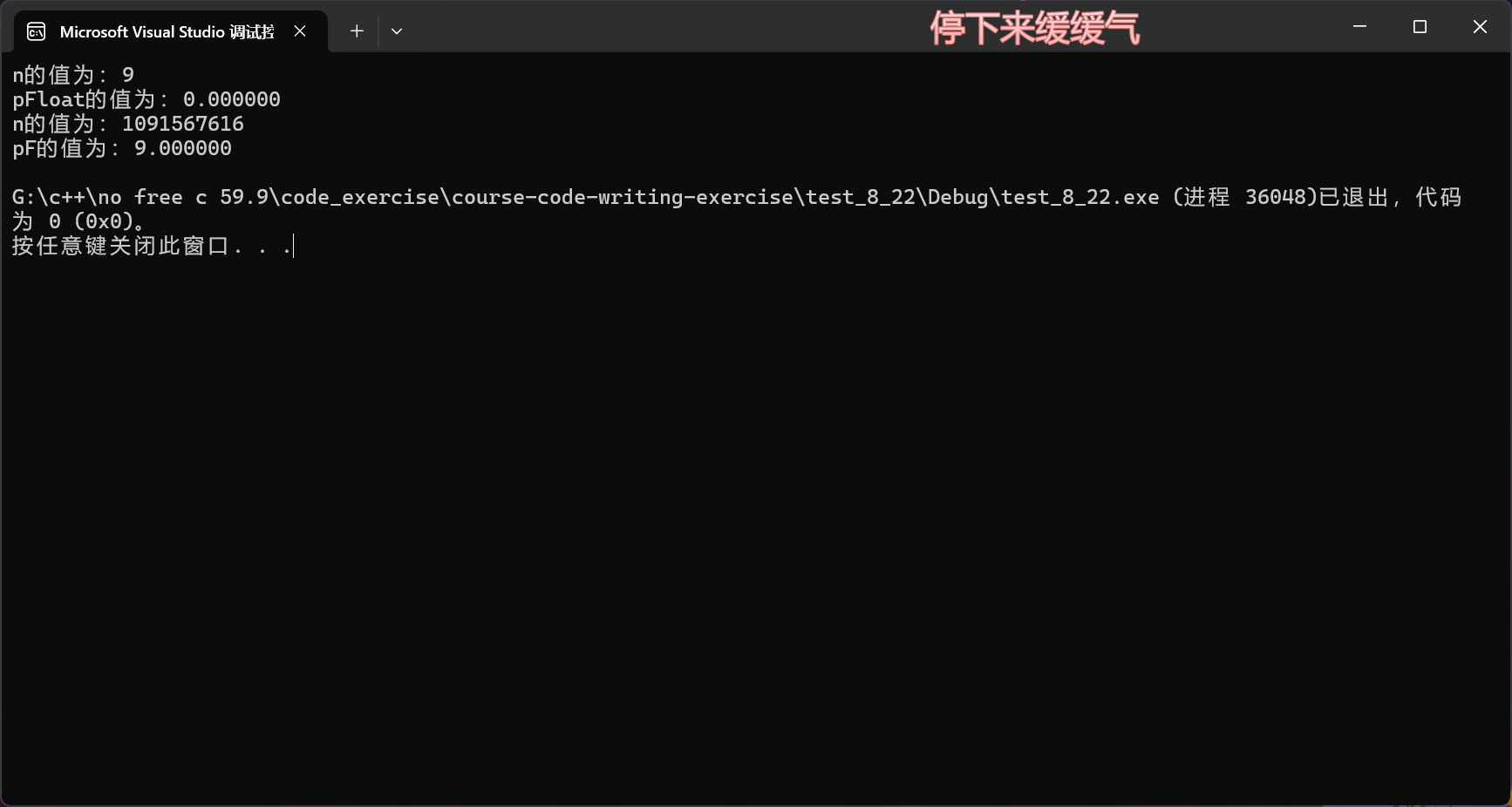
可以得出：浮點數在內存中的存儲和整數是不同的。

3.1?浮點數存儲的過程

上面的代碼中，n和*pFloat在內存中存儲的明明是同一個數，為什么浮點數和整數的解讀結果會差別那么大？

要理解這個結果，我們需要 搞懂浮點數在計算機內部的表示方法。

根據國際標準IEEE（電氣和電子工程協會）754，任意一個二進制浮點數V可以表示為下面的形式：

V = (-1)^S?* M * 2^E

????????(-1)^S表示符號位，當S=0，V為正數；當S=1，V為負數

????????M表示有效數字，M是大于等于1，小于2的

????????2^E表示的是指數位

舉例來說：

十進制的5.0，寫成二進制是101.0 -- 1.01*2^2。

那么，按照上面V的格式，可以得出S=0，M = 1.01，E = 2。

IEEE754規定：

對于32位的浮點數（float），最高的1位存儲符號位S，接著的8位存儲指數E，剩下的23位存儲有效數字M。

對于64位的浮點數（double），最高的1位存儲符號位S，接著的11位存儲指數E，剩下的52位存儲有效數字M。

IEEE754對有效數字M和指數E，還有一些特別的規定。

前面說過，1 <= M < 2,也就是說M可以寫成1.xxxxxx的形式，其中xxxxxx表示小數部分。

IEEE754規定，在計算機內部保存M時，默認這個數第一位總是1，因此可以舍棄，只保存后面的小數部分。比如說保存1.01時，只保存01，等到讀取的時候，再把第一位的1加上去，這樣做的目的，是節省1位有效數字。以32位浮點數為例，留給M只有23位，將第1位舍棄后，可以保存24位有效數字。

E是一個無符號整數（unsigned int）

這意味著，如果E為8位，它的取值范圍是0~255；如果E為11位，它的取值范圍為0~2047.但是，我們知道，科學計數法中的E是可以出現負數的，所以IEEE754規定，存入內存的E真實值必須再加上一個中間數，對于8位的E，這個中間數是127；對于11位的E，這個中間數是1023.

就拿9.5舉個例子：

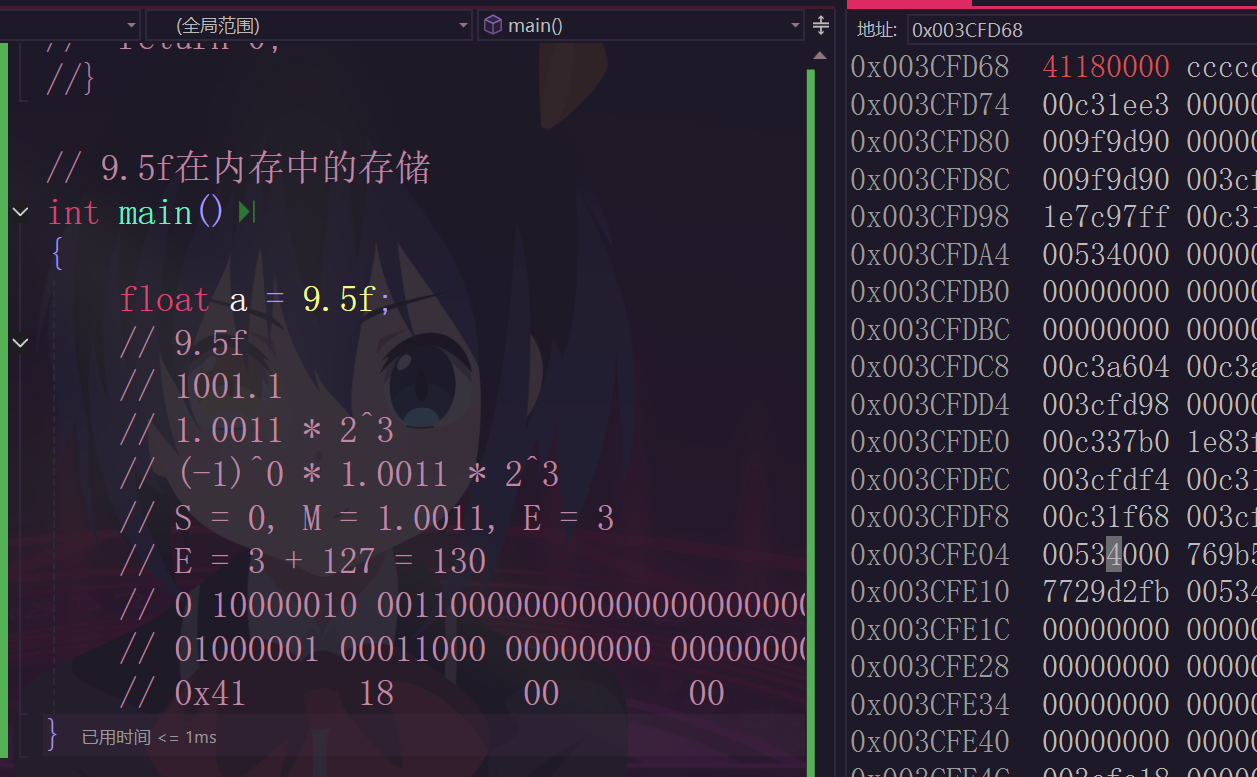
浮點數是有可能無法精確保存的，比如說1.2。

3.2?浮點數的取出過程

E不全為0或不全為1（常規情況）

這時，指數E的計算值-127（或1023），得到真實值，再將有效數字M前加上第1位的1。

E全為0

E等于1-127（或1-1023）即為真實值，有效數字M不再加上第一位的1，而是還原為0.xxxxxx的小數，這樣做是為了表示接近0很小的數字。

E全為1

如果有效數字M全為0，表示無窮大；