
?🔥個人主頁:艾莉絲努力練劍
?專欄傳送門:《C語言》、《數據結構與算法》、C語言刷題12天IO強訓、LeetCode代碼強化刷題、洛谷刷題、C/C++基礎知識知識強化補充、C/C++干貨分享&學習過程記錄
🍉學習方向:C/C++方向學習者
??人生格言:為天地立心,為生民立命,為往圣繼絕學,為萬世開太平
前言:距離我們學完C語言已經過去一段時間了,不知道大家還記不記得博主挖過的一個坑——就是在【掌握遞歸】函數遞歸思想的形成及其應用中介紹斐波那契數列的時候提到的青蛙跳臺階、漢諾塔問題,博主回收伏筆啦!希望大家能夠有所收獲!
目錄
補充兩者特點:遞歸VS迭代
0.1? 遞歸
0.2? 迭代
0.3? 學習數據結構之后
正文
一、遞歸 (Recursion)
1.1? 什么是遞歸
1.2? 遞歸的三大要素
1.3? 遞歸的優缺點
1.3.1? 優點
1.3.1? 缺點
二、迭代 (Iteration)
2.1? 什么是迭代(簡單理解就是循環)
2.2? 迭代的要素
2.3? 迭代 vs. 遞歸
三、斐波那契數列 (Fibonacci Sequence)
3.1? 問題描述
3.2? 斐波那契數列實現
3.2.1? 方法一:遞歸實現 (不推薦)
3.2.2? 方法二:迭代實現 (推薦)
四、漢諾塔問題 (Tower of Hanoi)
4.1? 問題描述
4.2? 遞歸思路
4.3? 漢諾塔問題實現
五、青蛙跳臺階問題
5.1? 問題描述
5.2? 問題分析
5.3? 代碼實現 (迭代,推薦)
5.4? 變種問題
六、總結環節(以表格形式呈現)
七、測試
結尾

補充兩者特點:遞歸VS迭代
0.1? 遞歸
(1)會占用更多的內存空間,有可能導致棧溢出的問題;
(2)性能的下降;
(3)有的復雜問題使用遞歸描述會很簡潔,寫成代碼也非常的方便。
0.2? 迭代
(1)效率高;
(2)迭代的方式有時候不容易想到。
0.3? 學習數據結構之后
(1)寫成遞歸程序,就幾行代碼;
(2)但是,不允許使用遞歸的時候,可能得寫幾十行代碼。
正文
一、遞歸 (Recursion)
比如這段代碼就是遞歸——
#include <stdio.h>// 遞歸計算階乘示例
int factorial(int n) {// 1. 遞歸終止條件if (n == 0 || n == 1) {return 1;}// 2. 遞歸調用:縮小問題規模return n * factorial(n - 1);
}int main()
{printf("5! = %d\n", factorial(5)); // 輸出 120return 0;
}1.1? 什么是遞歸
遞歸是一種解決問題的方法,它把一個問題分解為一個或多個規模更小的同類子問題,直到子問題簡單到可以直接解決。
遞歸的核心思想是自我調用。一個遞歸函數會直接或間接地調用自身。
比如這種——
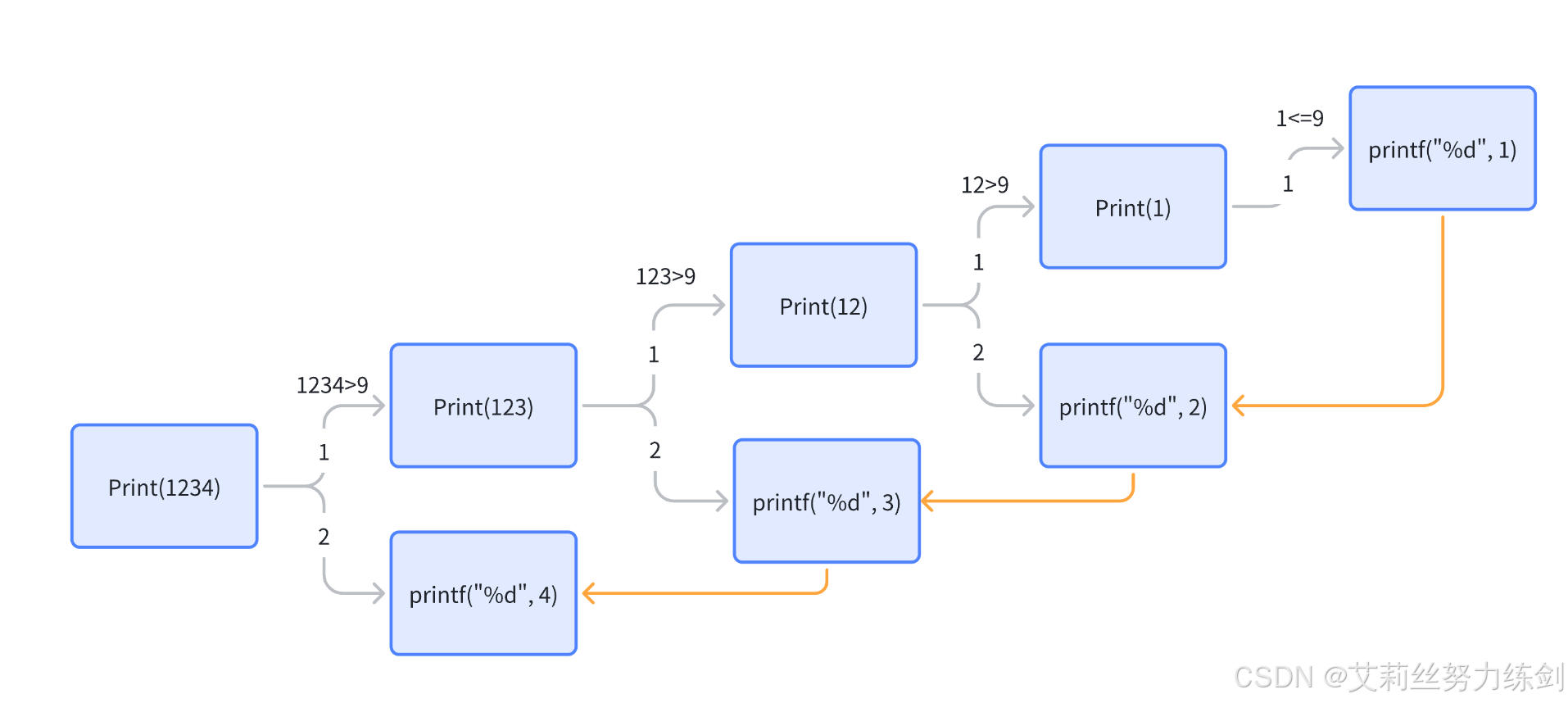
再比如說像這種——
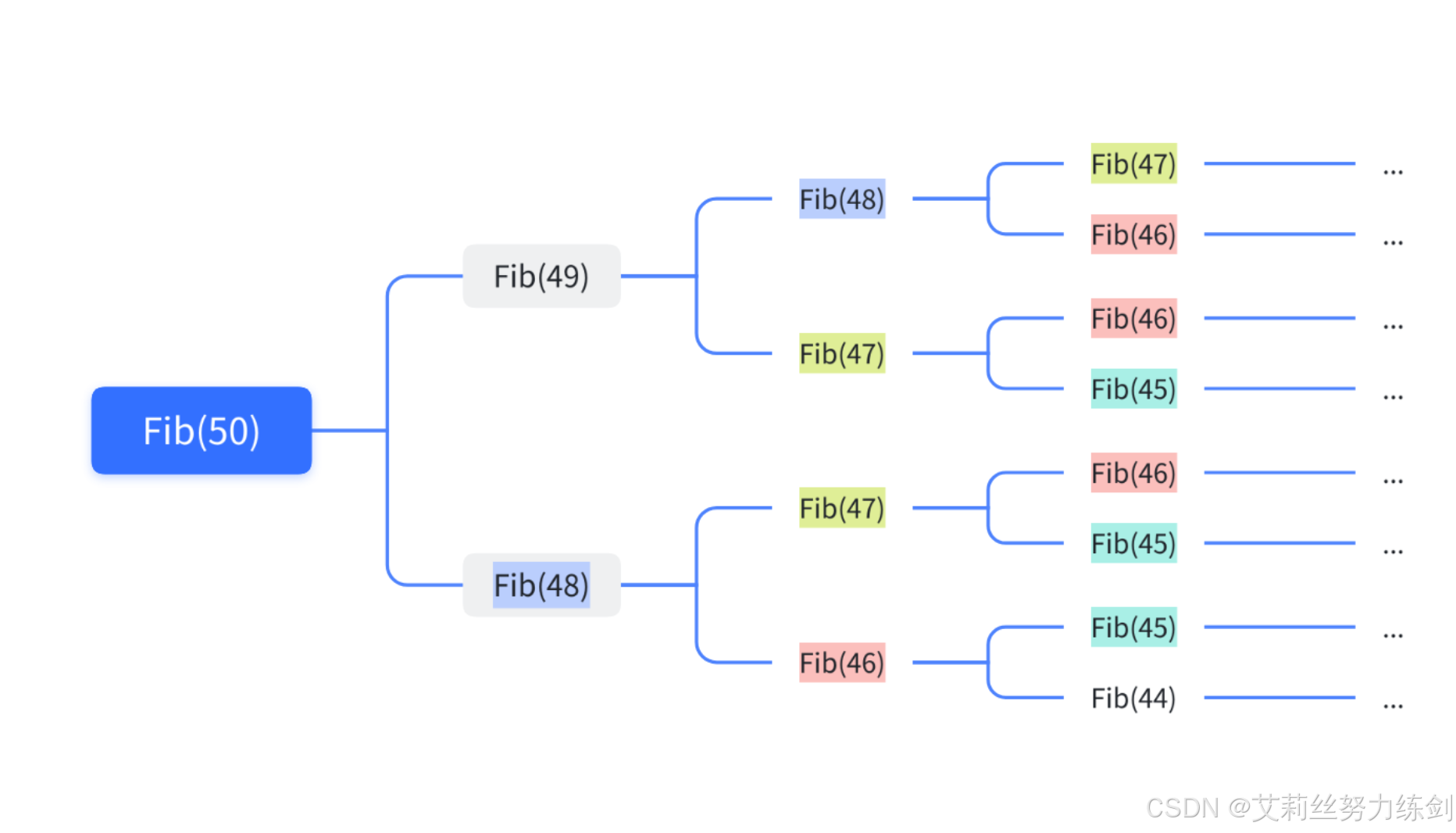
1.2? 遞歸的三大要素
1、明確遞歸終止條件 (Base Case):必須有一個明確的遞歸結束條件,也稱為“出口”。否則,函數會無限調用自己,導致棧溢出錯誤。
2、給出遞歸終止時的處理辦法:當Base Case被觸發時,應該直接返回一個明確的值。
3、提取重復邏輯,縮小問題規模 (Recursive Case):每次遞歸調用都應該是為了解決一個更小、更接近終止條件的子問題。
1.3? 遞歸的優缺點
1.3.1? 優點
代碼簡潔、清晰,對于解決一些本質就是遞歸定義的問題(如樹、圖的遍歷)非常有效。
1.3.1? 缺點
(1)棧溢出風險 (Stack Overflow):每次函數調用都會在內存棧中分配空間,遞歸深度過大會耗盡棧空間。
(2)重復計算:如斐波那契數列的遞歸實現,會進行大量重復計算,效率低下。
(3)時間和空間復雜度高:函數調用的開銷比循環大。
二、迭代 (Iteration)
迭代代碼演示:
#include <stdio.h>// 迭代計算階乘示例
int factorial_iter(int n) {int result = 1;for (int i = 1; i <= n; i++) {result *= i;}return result;
}int main()
{printf("5! = %d\n", factorial_iter(5)); // 輸出 120return 0;
}2.1? 什么是迭代(簡單理解就是循環)
迭代是一種利用循環結構(如?for,while,do...while)來重復執行一段代碼,通過變量的不斷更新來逐步逼近答案的方法。
2.2? 迭代的要素
-
循環條件:控制循環何時繼續、何時終止。
-
計數器/狀態變量:在循環過程中不斷更新,記錄當前的狀態或進度。
-
循環體:需要重復執行的核心邏輯。
2.3? 迭代 vs. 遞歸
| 特性 | 遞歸 (Recursion) | 迭代 (Iteration) |
|---|---|---|
| 實現 | 函數調用自身 | 循環結構 |
| 終止 | 終止條件 (Base Case) | 循環條件 |
| 效率 | 通常較低(函數調用開銷,棧空間占用) | 通常較高(無額外函數調用開銷) |
| 應用 | 樹、圖遍歷,分治,回溯等 | 大部分循環可以解決的問題 |
| 可讀性 | 對于遞歸問題,代碼更簡潔易讀 | 邏輯直白,但可能代碼更長 |
結論:所有遞歸問題都可以用迭代來實現,反之亦然。迭代通常效率更高,是遞歸的優化方向。選擇哪種方式取決于問題的性質和對效率的要求。
三、斐波那契數列 (Fibonacci Sequence)
3.1? 問題描述
斐波那契數列的定義是一個遞歸定義:
-
F(0) = 0
-
F(1) = 1
-
F(n) = F(n-1) + F(n-2) (n >= 2)
數列:0, 1, 1, 2, 3, 5, 8, 13, 21...
3.2? 斐波那契數列實現
3.2.1? 方法一:遞歸實現 (不推薦)
這是最直觀的實現,但效率極低。計算?fib(5)?的過程如下圖所示,充滿了重復計算,時間復雜度為O(2^n)。
代碼演示:
#include <stdio.h>int fib_recursive(int n) {// 遞歸終止條件if (n < 2) {return n;}// 遞歸調用:縮小規模return fib_recursive(n - 1) + fib_recursive(n - 2);
}int main()
{printf("fib(6) = %d\n", fib_recursive(6)); // 輸出 8return 0;
}3.2.2? 方法二:迭代實現 (推薦)
使用循環,從底向上計算,只需記錄前兩個狀態,時間復雜度為?O(n),空間復雜度為?O(1)。
代碼演示:
#include <stdio.h>int fib_iterative(int n) {if (n < 2) {return n;}int a = 0, b = 1; // 初始化前兩個數int temp;for (int i = 2; i <= n; i++) {temp = a + b; // 計算下一個數a = b; // 更新ab = temp; // 更新b}return b;
}int main()
{printf("fib(6) = %d\n", fib_iterative(6)); // 輸出 8return 0;
}四、漢諾塔問題 (Tower of Hanoi)
4.1? 問題描述
有三根柱子(A, B, C),A柱子上從下到上按從大到小的順序摞著n個圓盤。要求借助B柱子,將A柱子上的所有圓盤移動到C柱子上,并且每次只能移動一個盤子,且大盤子不能放在小盤子上面。
4.2? 遞歸思路
4.2.1? Base Case:
如果只有1個盤子,直接將它從 A 移動到 C。
?4.2.2? Recursive Case:
a. 將 A 上面的?
n-1?個盤子借助 C?移動到 B。
b. 將 A 最底下的第?n?個盤子直接移動到 C。
c. 將 B 上的?n-1?個盤子借助 A?移動到 C。
時間復雜度:O(2^n),移動步數是 2^n - 1。
4.3? 漢諾塔問題實現
C語言代碼演示:
#include <stdio.h>/*** @param n: 盤子數量* @param source: 源柱子 (起點)* @param auxiliary: 輔助柱子 (中轉站)* @param target: 目標柱子 (終點)*/
void hanoi(int n, char source, char auxiliary, char target) {if (n == 1) {// 遞歸終止條件:只有一個盤子,直接移動printf("Move disk 1 from %c to %c\n", source, target);return;}// Step 1: 將 n-1 個盤子從 source 借助 target 移動到 auxiliaryhanoi(n - 1, source, target, auxiliary);// Step 2: 將第 n 個盤子從 source 直接移動到 targetprintf("Move disk %d from %c to %c\n", n, source, target);// Step 3: 將 n-1 個盤子從 auxiliary 借助 source 移動到 targethanoi(n - 1, auxiliary, source, target);
}int main()
{// 移動3個盤子,從A借助B到Chanoi(3, 'A', 'B', 'C');return 0;
}這是一個典型的接口型代碼。
輸出:
Move disk 1 from A to C
Move disk 2 from A to B
Move disk 1 from C to B
Move disk 3 from A to C
Move disk 1 from B to A
Move disk 2 from B to C
Move disk 1 from A to C五、青蛙跳臺階問題
5.1? 問題描述
一只青蛙一次可以跳上1級臺階,也可以跳上2級臺階。求該青蛙跳上一個 n 級的臺階總共有多少種跳法。
5.2? 問題分析
這其實是一個斐波那契數列的變種問題。
-
假設?
f(n)?是跳上 n 級臺階的跳法總數。 -
最后一步只有兩種可能:
-
跳1級臺階:那么前面?
n-1?級臺階有?f(n-1)?種跳法。 -
跳2級臺階:那么前面?
n-2?級臺階有?f(n-2)?種跳法。
-
-
因此,
f(n) = f(n-1) + f(n-2)。 -
Base Case:
-
f(1) = 1?(跳1級:一種方法) -
f(2) = 2?(跳2級:一次跳2級,或分兩次每次跳1級)
-
可以發現,除了初始項?f(1)=1, f(2)=2,遞推公式和斐波那契數列完全一樣。
5.3? 代碼實現 (迭代,推薦)
同樣,為了避免遞歸的低效,我們使用迭代方法。
代碼演示:
#include <stdio.h>int jump_floor(int n) {if (n <= 2) {return n;}int a = 1, b = 2; // a代表f(n-2),b代表f(n-1)int temp;for (int i = 3; i <= n; i++) {temp = a + b; // 計算f(n)a = b; // 更新a為f(n-2)b = temp; // 更新b為f(n-1)}return b;
}int main()
{printf("跳5級臺階的方法數: %d\n", jump_floor(5)); // 輸出 8return 0;
}5.4? 變種問題
如果青蛙一次可以跳 1級、2級... 或 n級,那么跳法總數是?2^(n-1),可以用數學歸納法證明。
六、總結環節(以表格形式呈現)
| 問題/概念 | 核心思想 | 推薦解法 | 關鍵點 |
|---|---|---|---|
| 遞歸 | 自我調用,分解為子問題 | - | 牢記三大要素,尤其是終止條件 |
| 迭代 | 循環結構,更新狀態變量 | - | 效率通常高于遞歸 |
| 斐波那契數列 | F(n)=F(n-1)+F(n-2) | 迭代 | 遞歸法有大量重復計算,必須優化 |
| 漢諾塔 | 分治思想,分解移動步驟 | 遞歸 | 理解“借助”的含義,遞歸思路最清晰 |
| 青蛙跳臺階 | 動態規劃/斐波那契數列 | 迭代 | 分析最后一步的可能性,得出遞推式 |
七、測試
在最后的最后,有了前面內容的鋪墊,我們寫一個完整的測試程序。
代碼演示——
#include <stdio.h>// 函數聲明
int factorial(int n);
int factorial_iter(int n);
int fib_recursive(int n);
int fib_iterative(int n);
void hanoi(int n, char source, char auxiliary, char target);
int jump_floor(int n);int main() {printf("=== 遞歸和迭代算法示例 ===\n\n");printf("1. 遞歸階乘: 5! = %d\n", factorial(5));printf("2. 迭代階乘: 5! = %d\n\n", factorial_iter(5));printf("3. 遞歸斐波那契(fib(6)): %d\n", fib_recursive(6));printf("4. 迭代斐波那契(fib(6)): %d\n\n", fib_iterative(6));printf("5. 青蛙跳5級臺階的方法數: %d\n\n", jump_floor(5));printf("6. 漢諾塔問題 (3個盤子):\n");hanoi(3, 'A', 'B', 'C');return 0;
}// 函數定義
int factorial(int n) {if (n == 0 || n == 1) {return 1;}return n * factorial(n - 1);
}int factorial_iter(int n) {int result = 1;for (int i = 1; i <= n; i++) {result *= i;}return result;
}int fib_recursive(int n) {if (n < 2) {return n;}return fib_recursive(n - 1) + fib_recursive(n - 2);
}int fib_iterative(int n) {if (n < 2) {return n;}int a = 0, b = 1;int temp;for (int i = 2; i <= n; i++) {temp = a + b;a = b;b = temp;}return b;
}void hanoi(int n, char source, char auxiliary, char target) {if (n == 1) {printf("Move disk 1 from %c to %c\n", source, target);return;}hanoi(n - 1, source, target, auxiliary);printf("Move disk %d from %c to %c\n", n, source, target);hanoi(n - 1, auxiliary, source, target);
}int jump_floor(int n)
{if (n <= 2) {return n;}int a = 1, b = 2;int temp;for (int i = 3; i <= n; i++) {temp = a + b;a = b;b = temp;}return b;
}編譯和運行一下:
gcc -o recursion_examples recursion_examples.c
./recursion_examples最后,博主想說,理解這些經典問題,對于掌握算法設計和分析的基本思想至關重要。
結尾
往期回顧:
深入詳解C語言數組:承上啟下——從C語言數組基礎到數據結構銜接
結語:感謝大家的閱讀,記得給博主“一鍵四連”,感謝友友們的支持和鼓勵!


)

)




:mybaits if標簽test條件判斷等號=解析異常解決方案)









