HUMS問答:https://humsconference.com.au/HUMS2023datachallenge/questions-answers.html
數據集申請:https://www.dst.defence.gov.au/our-technologies/helicopter-main-rotor-gearbox-planet-gear-fatigue-crack-propagation-test
歷年試卷:https://humsconference.com.au/Papers.html
參數
| 部件(Component) | 齒輪齒數(No. of Gear Teeth) | 嚙合頻率(Mesh Freq. (Hz)) |
|---|---|---|
| 輸入小齒輪(Input pinion) | 19 | 1900 |
| 輸入錐齒輪(Input bevel gear) | 71 | 1900 |
| 太陽輪(Sun gear) | 27 | 568 |
| 行星輪(Planet gear) | 35 | 568 |
| 齒圈(Ring gear) | 99 | 568 |
一、傳動說明
這是一份齒輪傳動系統部件的參數表,包含以下關鍵信息:
- 部件類型:涵蓋輸入小齒輪、輸入錐齒輪、太陽輪、行星輪、齒圈,對應傳動系統不同功能組件。
- 齒輪齒數:每個部件的齒輪 teeth 數量,是齒輪設計和傳動比計算的基礎參數。
- 嚙合頻率:齒輪嚙合時的頻率(單位 Hz ),反映齒輪運轉時的動態特性。例如輸入小齒輪和輸入錐齒輪嚙合頻率均為 1900Hz ,說明二者配對傳動;太陽輪、行星輪、齒圈嚙合頻率均為 568Hz ,屬于同一組行星排的嚙合頻率,可用于振動分析、故障診斷(如通過頻譜識別嚙合頻率異常判斷齒輪故障 )。
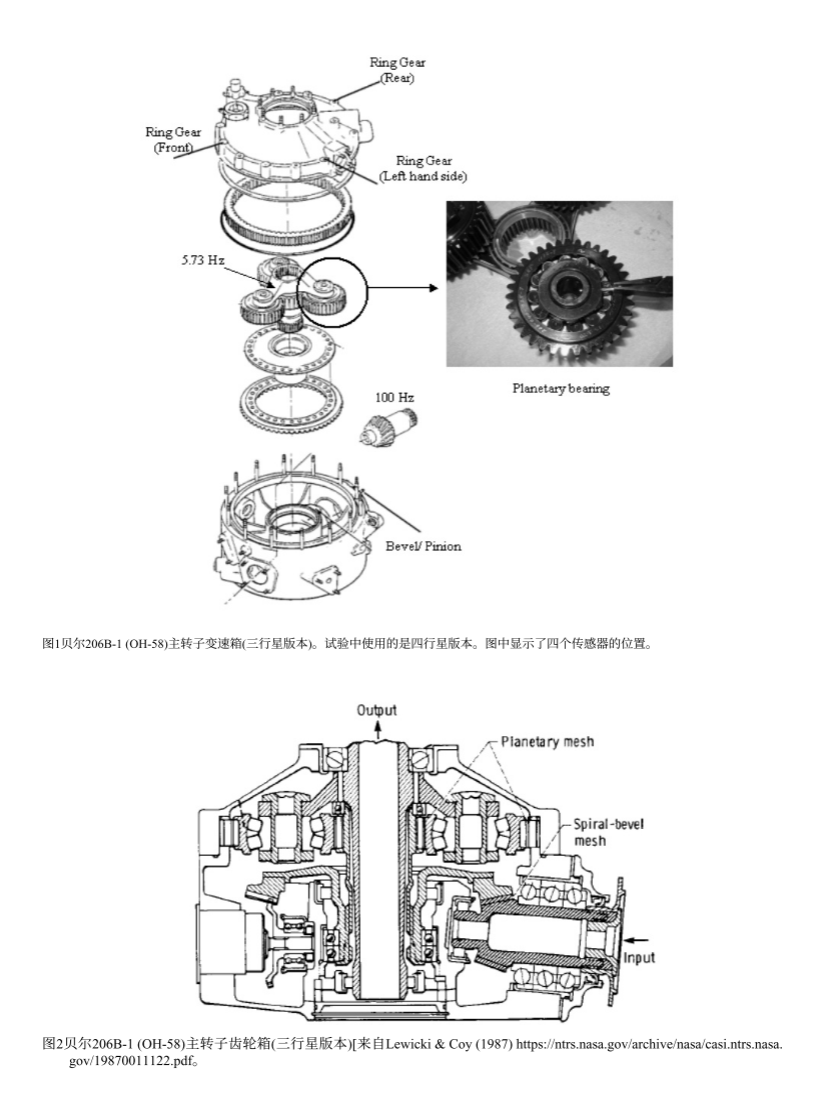
好的,根據您提供的兩張圖片中的信息,我們可以清晰地還原貝爾206B-1(OH-58)主旋翼變速箱的傳動原理。
這是一個兩級傳動的變速箱:
- 第一級:螺旋錐齒輪傳動 - 改變動力傳遞方向。
- 第二級:行星齒輪傳動 - 實現大的減速比。
其傳動路徑和原理如下圖所示:
二、關鍵參數與計算驗證
根據您提供的表1數據(輸入轉速6000 RPM或100 Hz),我們可以驗證一些關鍵頻率:
- 采樣頻率 (Input RPM): 526個mat文件,每個文件4個通道(傳感器),每個通道405405個數據,振動數據是同步平均的(即游動齒平均),因此數據是根據軸角(或轉數)而不是時間重新采樣的,每個數據文件的數據長度相當于約 6.1 秒(輸出軸旋轉 35 圈,因此 35 / 5.73333 = 6.1),基于標稱輸出軸轉速 5.73333 Hz。原始數據的原始采樣率為 65573.77049180328 Hz,由 NI-DAQ 板卡確定,但與平均數據無關。因此,用于計算齒間游動平均值的重采樣率為行星齒輪每轉 99 圈或行星架每轉 35 圈 405405 個樣本。
- 輸入軸轉頻: 6000 RPM / 60 = 100 Hz
- 螺旋錐齒輪嚙合頻率:
輸入小齒輪齒數 * 輸入軸轉頻= 19 teeth * 100 Hz = 1900 Hz ? - 行星級嚙合頻率(GMF):
太陽輪齒數 * 太陽輪絕對轉頻= 27 teeth * 21.05 Hz ≈ 568 Hz ?
📍 傳感器位置與監測點
圖1中標注的四個傳感器位置分別用于監測不同的故障特征:
- 輸入小齒輪:監測1900Hz附近的嚙合頻率及其邊帶。
- 齒圈前:監測568Hz附近的嚙合頻率及其邊帶。
- 齒圈左:監測軸承的故障特征頻率(如外圈、內圈、滾動體故障頻率)。
- 齒圈后:監測行星輪通過內齒圈局部缺陷時產生的低頻沖擊(如5.73Hz)。
這個變速箱的傳動設計非常經典:
- 錐齒輪級高效地改變了動力方向。
- 行星齒輪級在緊湊的空間內實現了巨大的減速比,輸出低轉速、高扭矩的動力來驅動主旋翼。
根據貝爾206B-1主旋翼變速箱的傳動原理和具體參數,我們現在可以系統地計算各個關鍵零件的理論故障特征頻率。
三、計算基礎參數
- 采樣頻率 (Input RPM): 原始數據的原始采樣率為 65573.77049180328 Hz
- 輸入轉速 (Input RPM): 6000 RPM
- 輸入轉頻 (Input Shaft Freq, finputf_{input}finput?): 600060=100?Hz\frac{6000}{60} = 100 \text{ Hz}606000?=100?Hz
- 行星架轉頻 (Carrier Freq, fcf_cfc?)): 約 5.73 Hz (根據圖1標注)
- 嚙合頻率 (Gear Mesh Frequency, GMF): 568 Hz (根據表1)
1. 螺旋錐齒輪級故障特征頻率
| 部件 | 故障特征 | 計算公式 | 計算值 (Hz) |
|---|---|---|---|
| 輸入小齒輪 | 轉頻 | finput=100?Hzf_{input} = 100 \text{ Hz}finput?=100?Hz | 100 |
| (19齒) | 局部故障頻率 | 1×finput1 \times f_{input}1×finput? | 100 |
| 2×finput2 \times f_{input}2×finput? | 200 | ||
| 錐齒輪 | 轉頻 | finput×NpinionNbevel=100×1971f_{input} \times \frac{N_{pinion}}{N_{bevel}} = 100 \times \frac{19}{71}finput?×Nbevel?Npinion??=100×7119? | 26.76 |
| (71齒) | 局部故障頻率 | 1×26.76?Hz1 \times 26.76 \text{ Hz}1×26.76?Hz | 26.76 |
| 嚙合點 | 嚙合頻率 | Npinion×finput=19×100N_{pinion} \times f_{input} = 19 \times 100Npinion?×finput?=19×100 | 1900 |
故障征兆:在振動頻譜中,若在1900 Hz的嚙合頻率及其諧波(3800 Hz, 5700 Hz…)周圍出現以100 Hz或26.76 Hz為間隔的邊帶,通常表明螺旋錐齒輪副中存在局部故障(如點蝕、裂紋)。
2. 行星齒輪級故障特征頻率
行星齒輪系統的故障特征頻率計算最為復雜,因為存在行星輪的公轉和自轉。
| 部件 | 故障特征 | 計算公式 | 計算值 (Hz) |
|---|---|---|---|
| 太陽輪 | 絕對轉頻 | fc×(1+NrNs)=5.73×(1+9927)f_{c} \times (1 + \frac{N_r}{N_s}) = 5.73 \times (1 + \frac{99}{27})fc?×(1+Ns?Nr??)=5.73×(1+2799?) | 26.76 (與錐齒輪同軸) |
| (27齒) | 局部故障頻率 (FTF) | NrNs×fc=9927×5.73\frac{N_r}{N_s} \times f_c = \frac{99}{27} \times 5.73Ns?Nr??×fc?=2799?×5.73 | 21.0 |
| 故障通過頻率 | Nplanets×fc=4×5.73N_{planets} \times f_c = 4 \times 5.73Nplanets?×fc?=4×5.73 | 22.92 | |
| 行星輪 | 自轉轉頻 | fc×NrNp=5.73×9935f_c \times \frac{N_r}{N_p} = 5.73 \times \frac{99}{35}fc?×Np?Nr??=5.73×3599? | 16.21 |
| (35齒, 4個) | 公轉轉頻 | fc=5.73f_c = 5.73fc?=5.73 | 5.73 |
| 局部故障頻率 (FTF) | 2×fc×NrNp=2×5.73×99352 \times f_c \times \frac{N_r}{N_p} = 2 \times 5.73 \times \frac{99}{35}2×fc?×Np?Nr??=2×5.73×3599? | 32.42 | |
| 內齒圈 | 局部故障頻率 | Nplanets×fc=4×5.73N_{planets} \times f_c = 4 \times 5.73Nplanets?×fc?=4×5.73 | 22.92 |
| (99齒, 固定) | 行星輪通過頻率 | Nplanets×fc=4×5.73N_{planets} \times f_c = 4 \times 5.73Nplanets?×fc?=4×5.73 | 22.92 |
| 行星架 | 轉頻 | fc=5.73f_c = 5.73fc?=5.73 | 5.73 |
| 嚙合點 | 嚙合頻率 (GMF) | Ns×(fs)=27×26.76≈568N_s \times (f_s) = 27 \times 26.76 \approx 568Ns?×(fs?)=27×26.76≈568 | 568 |
故障征兆:
- 太陽輪/行星輪故障:在568 Hz的嚙合頻率及其諧波周圍,出現以太陽輪FTF(21.0 Hz) 或行星輪FTF(32.42 Hz) 為間隔的邊帶。
- 內齒圈故障:在嚙合頻率周圍出現以行星輪通過頻率(22.92 Hz) 為間隔的邊帶。
- 行星輪局部故障:其振動信號還會被其公轉頻率(5.73 Hz) 調制。
3. 行星輪軸承故障特征頻率
行星輪軸承的故障頻率計算需要其幾何參數(滾子數、節徑、接觸角等),這些參數通常未在您提供的資料中給出。但其計算邏輯如下:
| 故障類型 | 大致計算公式(需具體參數) | 說明 |
|---|---|---|
| 內圈故障 | BPFI≈Nb2×frotor×(1+BdPdcos?θ)BPFI \approx \frac{N_b}{2} \times f_{rotor} \times (1 + \frac{B_d}{P_d} \cos\theta)BPFI≈2Nb??×frotor?×(1+Pd?Bd??cosθ) | frotorf_{rotor}frotor? 為行星輪自轉頻率(16.21 Hz) |
| 外圈故障 | BPFO≈Nb2×frotor×(1?BdPdcos?θ)BPFO \approx \frac{N_b}{2} \times f_{rotor} \times (1 - \frac{B_d}{P_d} \cos\theta)BPFO≈2Nb??×frotor?×(1?Pd?Bd??cosθ) | 外圈固定,故障頻率穩定,在頻譜中表現為清晰譜線 |
| 滾動體故障 | BSF≈Pd2×Bd×frotor×(1?(BdPdcos?θ)2)BSF \approx \frac{P_d}{2 \times B_d} \times f_{rotor} \times (1 - (\frac{B_d}{P_d} \cos\theta)^2)BSF≈2×Bd?Pd??×frotor?×(1?(Pd?Bd??cosθ)2) | |
| 保持架故障 | FTF≈12×frotor×(1?BdPdcos?θ)FTF \approx \frac{1}{2} \times f_{rotor} \times (1 - \frac{B_d}{P_d} \cos\theta)FTF≈21?×frotor?×(1?Pd?Bd??cosθ) |
關鍵點:即使沒有精確幾何參數,也應知道行星輪軸承的所有故障頻率都以其自轉頻率(16.21 Hz) 為基頻,并被其公轉頻率(5.73 Hz) 調制。因此,在頻譜中尋找以~16.21 Hz及其倍頻為間隔的譜線,是診斷行星輪軸承故障的起點。
總結與故障診斷策略
- 定位嚙合頻率:首先在頻譜中找到1900 Hz(錐齒輪)和568 Hz(行星齒輪)的嚙合頻率及其諧波。
- 尋找邊帶:這是診斷的關鍵。仔細觀察嚙合頻率譜線兩側是否存在邊帶。
- 邊帶間隔為 100 Hz → 懷疑輸入小齒輪。
- 邊帶間隔為 26.76 Hz → 懷疑錐齒輪或太陽輪。
- 邊帶間隔為 21.0 Hz → 懷疑太陽輪局部故障。
- 邊帶間隔為 22.92 Hz → 懷疑內齒圈或行星輪通過頻率。
- 邊帶間隔為 32.42 Hz → 懷疑行星輪局部故障。
- 低頻段分析:在低頻段(< 100 Hz)尋找 5.73 Hz(行星架/行星輪公轉)、16.21 Hz(行星輪自轉)、21.0 Hz(太陽輪FTF)等頻率成分,它們本身的幅值升高也可能預示相應部件的故障。
- 包絡譜分析:對原始振動信號(或經濾波后的信號)進行包絡譜分析,能極大地增強對軸承和齒輪局部故障沖擊的識別能力,是診斷這類故障最有效的方法之一。

![[docker/大數據]Spark快速入門](http://pic.xiahunao.cn/[docker/大數據]Spark快速入門)





)

)




:mybaits if標簽test條件判斷等號=解析異常解決方案)




