數據結構之深入探索快速排序

基準值的選定

我們之前已經用四種不同的方式實現了快速排序，如果還沒有學習過的伙伴們可以看一下這篇文章哦：數據結構之排序大全（3）-CSDN博客

那我們既然已經學習了這么多種方法，為什么還要繼續探索快速排序呢？

那是因為我們之前寫的排序算法雖然在大部分情況下可以高效率地解決排序問題（效率較高的情況下，遞歸產生的遞歸樹形狀是完全二叉樹的結構），時間復雜度是O(n*logN）但是在一些極端的情況下，算法的時間復雜度會退化成O(N^2)。這是咋回事呢？

我們在上面的博客中已經舉過一個例子：當數組已經處于排好序的狀態時，形成的遞歸深度h=n，這句會導致時間復雜度退化成O(N^2)。

這是因為我們指定了最左邊的數作為基準值，而當數組已經有序時，每次選擇最左邊元素作為基準值會導致分區極度不平衡，一邊永遠為空，另一邊包含所有剩余元素，使得遞歸深度從 O(log n) 退化為 O(n)，時間復雜度從 O(n log n) 退化為 O(n2)。對已排序的數組，選最左基準值會導致快速排序退化成冒泡排序，每次只能處理一個元素。

上面問題的發生就是因為我們選基準值選的不太好，有沒有什么解決方法呢？

當然是有的，既然根本原因就是我們的基準值選的不好，那我們就重新選定基準值就好了呀。

隨機選定基準值當然可以使用生成隨機數的函數：

int randi = left + (rand() % (right-left + 1));

這個公式是怎么來的呢？

我們知道任意一個數模除x的范圍在0~x-1，那么任意一個數模除x+1的范圍就在0~x之間，那么任意一個數模除right-left+1的范圍就在0~right-left之間，那么left+rand()%(right-left+1)的范圍就在left~right之間。

如果我們要在代碼中使用隨機數位置的數值作為基準值，那就將代碼寫成：

#include<stdlib.h>
#include<time.h>//交換元素
void swap(int* px, int* py)
{int tmp = *px;*px = *py;*py = tmp;
}//指定基準值，將基準值放到對應的位置，函數會返回基準值的下標
int _QuickSort_Hoare(int* arr, int left, int right)
{int randi =left+rand()%(right-left+1)swap(&arr[randi], &arr[left]);//指定基準值為左端點位置上的數int keyi = left;//left從左往右走，找比基準值大的數//keyi初始與left指向相同，不妨就先讓left向右走一步left++;//right從右往左走，找比基準值小的數while (left <= right){//在right和left移動的過程中始終要滿足left<=rightwhile (left <= right && arr[left] < arr[keyi]){left++;}while (left <= right && arr[right] > arr[keyi]){right--;}//走到這一步,有兩種可能：//1)   left>right//2）left<=right并且left指向的值大于arr[keyi]，right指向的值小于arr[keyi]if (left <= right){swap(&arr[left], &arr[right]);left++;right--;}}//此時left>right（left=right+1),那么就有right以及right前面的位置所存放的值都小于arr[keyi]//left以及left后面的位置所存放的值都大于arr[keyi]swap(&arr[keyi], &arr[right]);keyi = right;return keyi;
}int _QuickSort_Hole(int* arr, int left, int right)
{int randi =left+rand()%(right-left+1)swap(&arr[randi], &arr[left]);//指定基準值int key = arr[left];//挖坑int hole = left;while (left < right){//right從右往左找比基準值要小的while (left < right && arr[right] >= key){right--;}//將right位置存放的值拿去填坑arr[hole] = arr[right];//更新坑位hole = right;//left從左往右找比基準值大的while (left < right && arr[left] <= key){left++;}//將left位置存放的值拿去填坑arr[hole] = arr[left];//更新坑位hole = left;}//跳出循環，必有left==right，此時left和right都指向坑位hole//而hole就是基準值應該在的位置//用基準值填最后一個坑arr[hole] = key;return hole;
}int _QuickSort_lomuto(int* arr, int left, int right)
{int randi =left+rand()%(right-left+1)swap(&arr[randi], &arr[left]);int keyi = left;int prev = left;int pcur = prev + 1;while (pcur <= right){if (arr[pcur] < arr[keyi] && ++prev != pcur){swap(&arr[prev], &arr[pcur]);}pcur++;}//走到最后，prev的位置就是基準值應該存放的位置swap(&arr[prev], &arr[keyi]);return prev;
}//快速排序
//left表示序列的左端點下標  right表示序列的右端點下標
void QuickSort(int* arr, int left, int right)
{srand((unsigned int)time(NULL));if (left >= right)//左端點>=右端點，說明這個序列中已經有序{return;}//找基準值keyiint keyi = _QuickSort_lomuto(arr, left, right);//找到基準值后，將序列劃分：left  keyi   rightQuickSort(arr, left, keyi - 1);QuickSort(arr, keyi + 1, right);}

但是，我們使用隨機值在極端情況下也會不可避免的出現上面的問題，那還有沒有別的方法呢？

且看下面分解：

三數取中找基準值

我們要找一個基準值，使根據算法給基準值找到它應該在的位置的時候，我們可以根據基準值所在的位置將整個序列基本均分，那么我們找的基準值至少不能是序列中最大或者最小的值，這樣的話，我們就可以比較序列中左端點，右端點以及中間端點的值，找出這三個數中的中間值，如果用這個中間值來作為基準值，那么這個基準值一定不是整個序列中最大值或最小值,整個思路比較簡單，我們來寫一下代碼：

//三數取中
int GetMid(int* arr, int left, int right)
{int midi = (left + right) / 2;if (arr[left] < arr[midi]){if (arr[midi] < arr[right]){return  midi;}else if (arr[left] < arr[right]){return right;}else{return left;}}else//arr[left]>=arr[mid]{if (arr[midi] > arr[right]){return midi;}else if (arr[right] < arr[left]){return right;}else{return left;}}
}

我們接下來就利用一下這個代碼，在此之前，我們先用以下代碼測試一下原來快速排序對10萬個元素的有序序列進行排序的性能：

//test.c
#define  _CRT_SECURE_NO_WARNINGS 1
#include"sort.h"
// 測試排序的性能對?
void TestOP()
{//生成隨機數，將隨機數存入數組srand((unsigned int)time(0));const int N = 100000;int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a4[i] = rand();a5[i] = a4[i];}int begin4 = clock();HeapSort(a4, N);int end4 = clock();int begin5 = clock();QuickSort(a4, 0, N - 1);int end5 = clock();printf("HeapSort:%d\n", end4 - begin4);printf("QuickSort:%d\n", end5 - begin5);free(a4);free(a5);}int main()
{TestOP();return 0;
}
//sort.h
#pragma once#include<stdio.h>
#include<stdlib.h>
#include<time.h>//快速排序
void QuickSort(int* arr, int left, int right);//堆排序
void HeapSort(int* arr, int n);
//sort.c#define  _CRT_SECURE_NO_WARNINGS 1
#include"sort.h"
//交換元素
void swap(int* px, int* py)
{int tmp = *px;*px = *py;*py = tmp;
}//堆排序
//向下調整算法
void AdjustDown(int* arr, int n, int parent)
{int child = 2 * parent + 1;while (child < n){if (child + 1 < n && arr[child] < arr[child + 1])//此時默認是建立大堆{child++;}if (arr[parent] < arr[child]){swap(&arr[parent], &arr[child]);parent = child;child = 2 * parent + 1;}else{break;}}
}
void HeapSort(int* arr, int n)
{//先將元素建堆——利用向下調整算法//升序建大堆，降序建小堆//這里我們就選擇排升序for (int parent = (n - 1 - 1) / 2; parent >= 0; parent--){AdjustDown(arr, n, parent);}//建完堆以后，利用堆結構進行排序for (int size = n - 1; size > 0; size--){swap(&arr[0], &arr[size]);//對剩下的size個元素進行向下調整AdjustDown(arr, size, 0);}
}//指定基準值，將基準值放到對應的位置，函數會返回基準值的下標
int _QuickSort_Hoare(int* arr, int left, int right)
{//指定基準值為左端點位置上的數int keyi = left;//left從左往右走，找比基準值大的數//keyi初始與left指向相同，不妨就先讓left向右走一步left++;//right從右往左走，找比基準值小的數while (left <= right){//在right和left移動的過程中始終要滿足left<=rightwhile (left <= right && arr[left] < arr[keyi]){left++;}while (left <= right && arr[right] > arr[keyi]){right--;}//走到這一步,有兩種可能：//1)   left>right//2）left<=right并且left指向的值大于arr[keyi]，right指向的值小于arr[keyi]if (left <= right){swap(&arr[left], &arr[right]);left++;right--;}}//此時left>right（left=right+1),那么就有right以及right前面的位置所存放的值都小于arr[keyi]//left以及left后面的位置所存放的值都大于arr[keyi]swap(&arr[keyi], &arr[right]);keyi = right;return keyi;
}int _QuickSort_Hole(int* arr, int left, int right)
{//指定基準值int key = arr[left];//挖坑int hole = left;while (left < right){//right從右往左找比基準值要小的while (left < right && arr[right] >= key){right--;}//將right位置存放的值拿去填坑arr[hole] = arr[right];//更新坑位hole = right;//left從左往右找比基準值大的while (left < right && arr[left] <= key){left++;}//將left位置存放的值拿去填坑arr[hole] = arr[left];//更新坑位hole = left;}//跳出循環，必有left==right，此時left和right都指向坑位hole//而hole就是基準值應該在的位置//用基準值填最后一個坑arr[hole] = key;return hole;
}int _QuickSort_lomuto(int* arr, int left, int right)
{int keyi = left;int prev = left;int pcur = prev + 1;while (pcur <= right){if (arr[pcur] < arr[keyi] && ++prev != pcur){swap(&arr[prev], &arr[pcur]);}pcur++;}//走到最后，prev的位置就是基準值應該存放的位置swap(&arr[prev], &arr[keyi]);return prev;
}//快速排序
//left表示序列的左端點下標  right表示序列的右端點下標
void QuickSort(int* arr, int left, int right)
{if (left >= right)//左端點>=右端點，說明這個序列中已經有序{return;}//找基準值keyiint keyi = _QuickSort_lomuto(arr, left, right);//找到基準值后，將序列劃分：left  keyi   rightQuickSort(arr, left, keyi - 1);QuickSort(arr, keyi + 1, right);}

上面的代碼中，我們先利用堆排序使得10萬個數據有序，然后再用快速排序對這10萬個數據進行排序,看一下效果：

測試環境：Debug,x86

我們可以看到，代碼崩潰了，這真的很令人奇怪了，注意哦，小編這里已經用較小的數據集合對代碼測試過了，代碼運行是沒有問題的。

Debug版本包含了許多調試信息，而Release版本的代碼就進行了較多的優化，我們要不試試release版本呢？

運行結果：

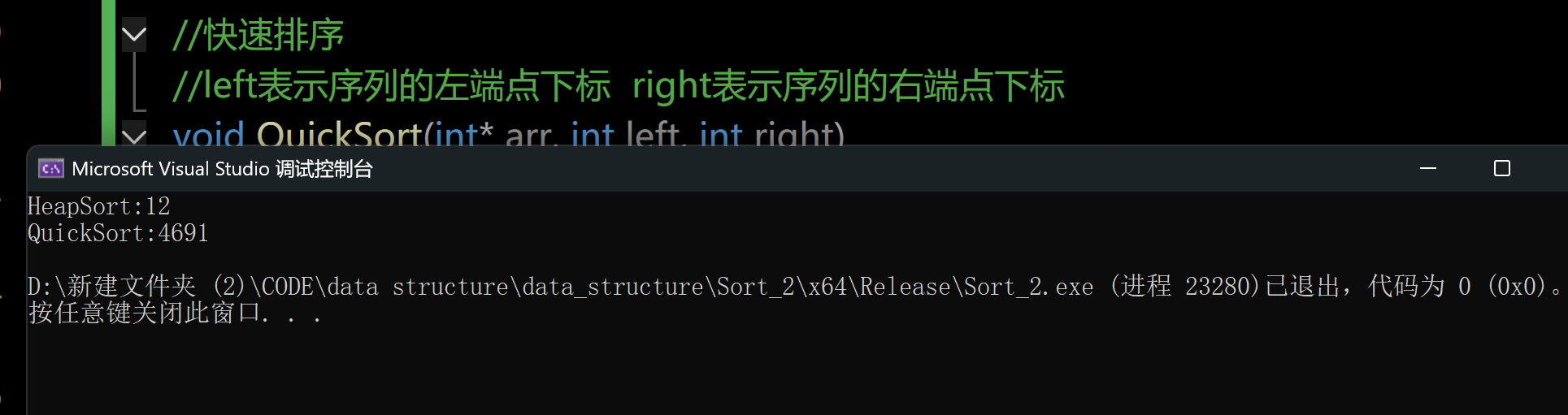
可以看到，release版本下我們的代碼可以正常運行，說明我們的代碼本身并沒有錯誤，而且我們可以看到快速排序的時間性能比起堆排序慢的太多了。

我們在通過調試過程看一下為什么在Debug版本下代碼崩潰了：

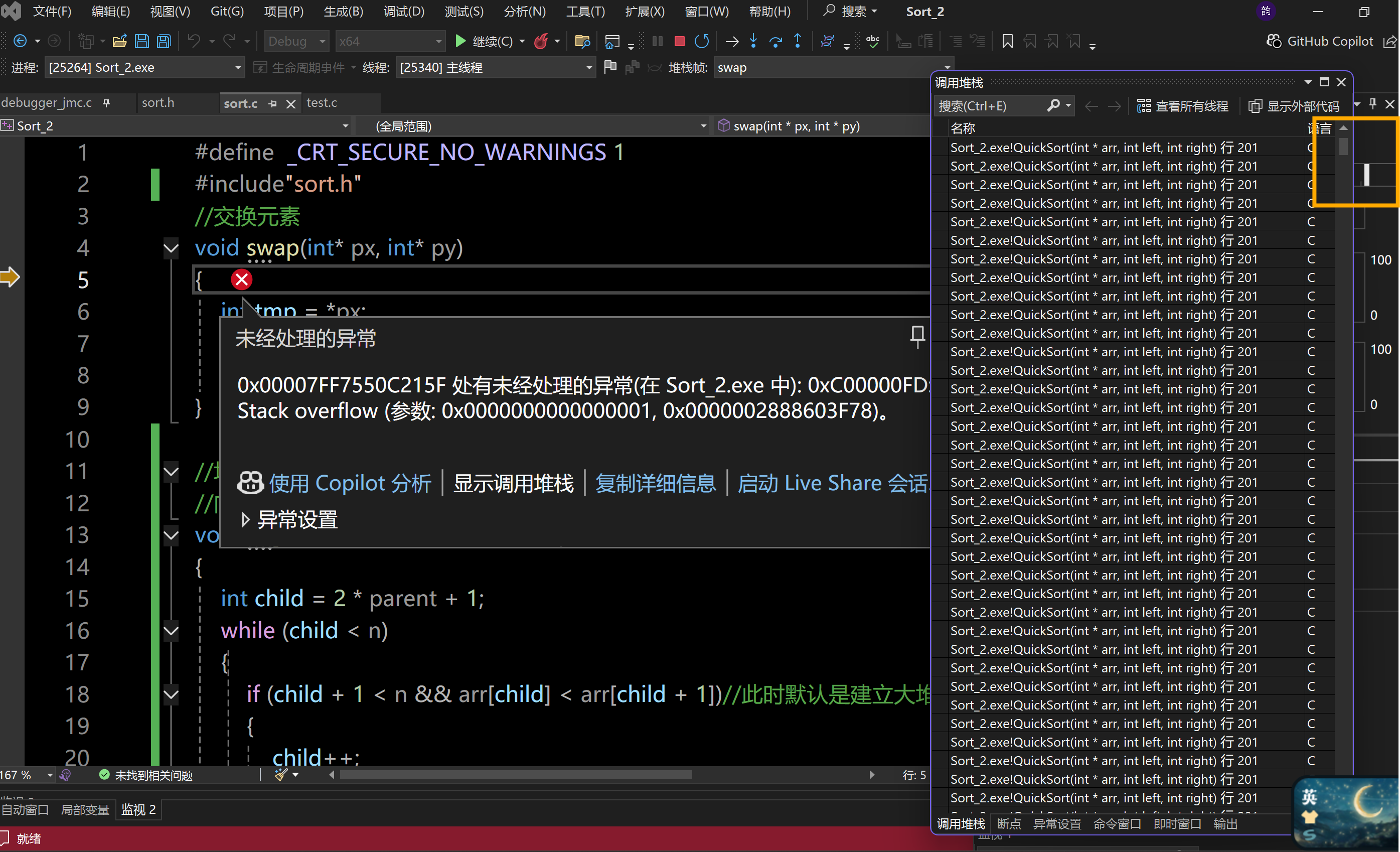
我們可以看到，調用堆棧的層次很深，代碼之所以崩潰是因為遞歸層次太深導致棧溢出了，這也是快速排序在對有序數組排序過程中的致命弱點。

那我們來試一試優化以后的快速排序呢：

//交換元素
void swap(int* px, int* py)
{int tmp = *px;*px = *py;*py = tmp;
}//三數取中
int GetMid(int* arr, int left, int right)
{int midi = (left + right) / 2;if (arr[left] < arr[midi]){if (arr[midi] < arr[right]){return  midi;}else if (arr[left] < arr[right]){return right;}else{return left;}}else//arr[left]>=arr[mid]{if (arr[midi] > arr[right]){return midi;}else if (arr[right] < arr[left]){return right;}else{return left;}}
}//指定基準值，將基準值放到對應的位置，函數會返回基準值的下標
int _QuickSort_Hoare(int* arr, int left, int right)
{int midi = GetMid(arr, left, right);swap(&arr[midi], &arr[left]);//指定基準值為左端點位置上的數int keyi = left;//left從左往右走，找比基準值大的數//keyi初始與left指向相同，不妨就先讓left向右走一步left++;//right從右往左走，找比基準值小的數while (left <= right){//在right和left移動的過程中始終要滿足left<=rightwhile (left <= right && arr[left] < arr[keyi]){left++;}while (left <= right && arr[right] > arr[keyi]){right--;}//走到這一步,有兩種可能：//1)   left>right//2）left<=right并且left指向的值大于arr[keyi]，right指向的值小于arr[keyi]if (left <= right){swap(&arr[left], &arr[right]);left++;right--;}}//此時left>right（left=right+1),那么就有right以及right前面的位置所存放的值都小于arr[keyi]//left以及left后面的位置所存放的值都大于arr[keyi]swap(&arr[keyi], &arr[right]);keyi = right;return keyi;
}int _QuickSort_Hole(int* arr, int left, int right)
{int midi = GetMid(arr, left, right);swap(&arr[midi], &arr[left]);//指定基準值int key = arr[left];//挖坑int hole = left;while (left < right){//right從右往左找比基準值要小的while (left < right && arr[right] >= key){right--;}//將right位置存放的值拿去填坑arr[hole] = arr[right];//更新坑位hole = right;//left從左往右找比基準值大的while (left < right && arr[left] <= key){left++;}//將left位置存放的值拿去填坑arr[hole] = arr[left];//更新坑位hole = left;}//跳出循環，必有left==right，此時left和right都指向坑位hole//而hole就是基準值應該在的位置//用基準值填最后一個坑arr[hole] = key;return hole;
}int _QuickSort_lomuto(int* arr, int left, int right)
{int midi = GetMid(arr, left, right);swap(&arr[midi], &arr[left]);int keyi = left;int prev = left;int pcur = prev + 1;while (pcur <= right){if (arr[pcur] < arr[keyi] && ++prev != pcur){swap(&arr[prev], &arr[pcur]);}pcur++;}//走到最后，prev的位置就是基準值應該存放的位置swap(&arr[prev], &arr[keyi]);return prev;
}//快速排序
//left表示序列的左端點下標  right表示序列的右端點下標
void QuickSort(int* arr, int left, int right)
{if (left >= right)//左端點>=右端點，說明這個序列中已經有序{return;}//找基準值keyiint keyi = _QuickSort_lomuto(arr, left, right);//找到基準值后，將序列劃分：left  keyi   rightQuickSort(arr, left, keyi - 1);QuickSort(arr, keyi + 1, right);}

我們只是在每個算法的里面加上了前面兩句代碼，重新指定基準值，其他邏輯全都不變，現在，我們再來測試一下算法：

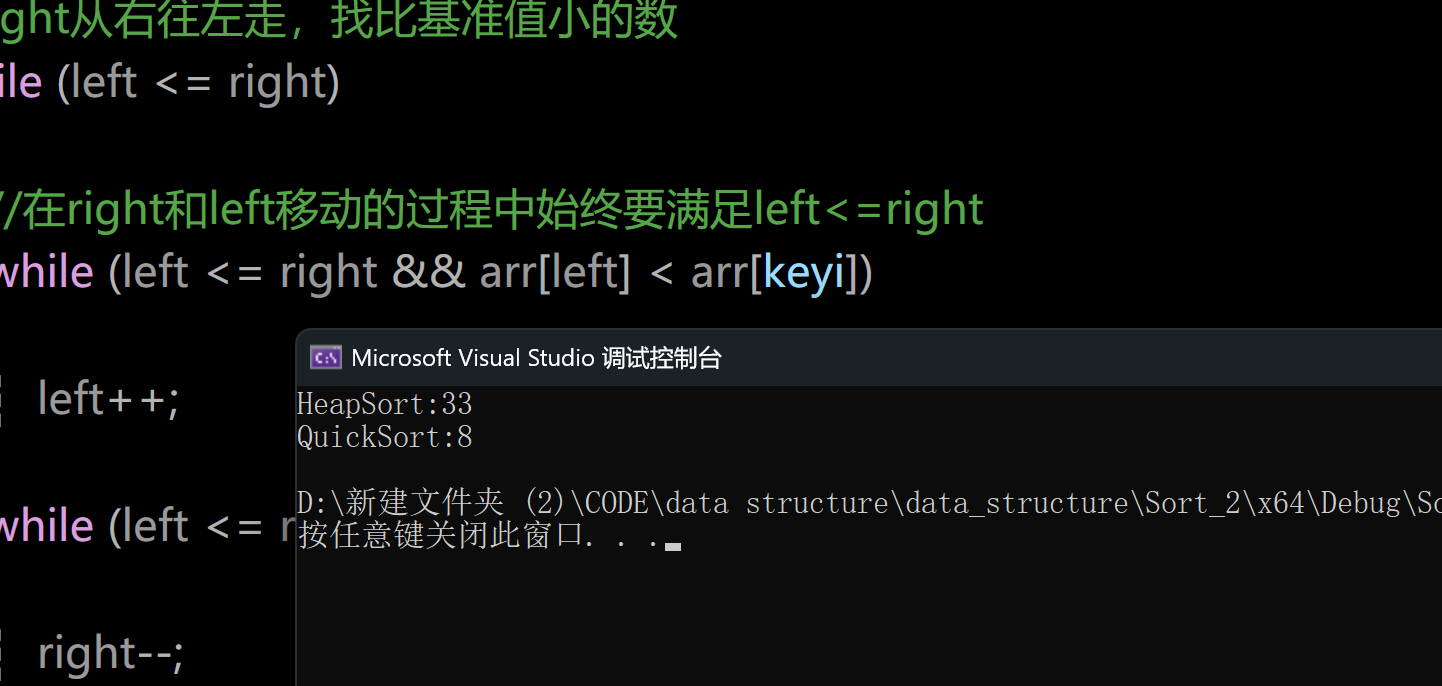
測試環境：Debug，可以看到快速排序在排序有序數組時的時間性能確實提高了。

快速排序的小區間優化

當快速排序遞歸到小區間時（通常是?10-20個元素），使用插入排序而不是繼續遞歸，這種優化稱為小區間優化。

?為什么要優化？

遞歸的成本：

  • 函數調用開銷：每次遞歸調用都需要創建棧幀、保存寄存器、傳遞參數等

  • 棧空間消耗：深度遞歸可能導致棧溢出

  • 緩存不友好：頻繁的函數調用破壞緩存局部性

插入排序的優勢：

  • 小數據量高效：當 n < 15 時，插入排序的實際性能比快速排序更好

  • 簡單直接：沒有函數調用開銷

  • 常數因子小：實際運行時間更少

插入排序我們之前已經寫過了，那我們現在就來直接寫一下優化后的代碼：

//交換元素
void swap(int* px, int* py)
{int tmp = *px;*px = *py;*py = tmp;
}
//三數取中
int GetMid(int* arr, int left, int right)
{int midi = (left + right) / 2;if (arr[left] < arr[midi]){if (arr[midi] < arr[right]){return  midi;}else if (arr[left] < arr[right]){return right;}else{return left;}}else//arr[left]>=arr[mid]{if (arr[midi] > arr[right]){return midi;}else if (arr[right] < arr[left]){return right;}else{return left;}}
}//直接插入排序
void InsertSort(int* arr, int n)
{for (int i = 0; i < n - 1; i++){int end = i;//end表示已經排好序列的最后一個元素的下標，初始已經排好的序列中只有一個元素//這個元素就是數組中的第一個元素，下標是0
//循環將end的下一個元素放到已經排好序的序列中int tmp = arr[end + 1];while (end >= 0){//找到tmp應該放在的位置if (arr[end] > tmp){arr[end + 1] = arr[end];end--;}else{break;}}arr[end + 1] = tmp;}
}//指定基準值，將基準值放到對應的位置，函數會返回基準值的下標
int _QuickSort_Hoare(int* arr, int left, int right)
{int midi = GetMid(arr, left, right);swap(&arr[midi], &arr[left]);//指定基準值為左端點位置上的數int keyi = left;//left從左往右走，找比基準值大的數//keyi初始與left指向相同，不妨就先讓left向右走一步left++;//right從右往左走，找比基準值小的數while (left <= right){//在right和left移動的過程中始終要滿足left<=rightwhile (left <= right && arr[left] < arr[keyi]){left++;}while (left <= right && arr[right] > arr[keyi]){right--;}//走到這一步,有兩種可能：//1)   left>right//2）left<=right并且left指向的值大于arr[keyi]，right指向的值小于arr[keyi]if (left <= right){swap(&arr[left], &arr[right]);left++;right--;}}//此時left>right（left=right+1),那么就有right以及right前面的位置所存放的值都小于arr[keyi]//left以及left后面的位置所存放的值都大于arr[keyi]swap(&arr[keyi], &arr[right]);keyi = right;return keyi;
}int _QuickSort_Hole(int* arr, int left, int right)
{int midi = GetMid(arr, left, right);swap(&arr[midi], &arr[left]);//指定基準值int key = arr[left];//挖坑int hole = left;while (left < right){//right從右往左找比基準值要小的while (left < right && arr[right] >= key){right--;}//將right位置存放的值拿去填坑arr[hole] = arr[right];//更新坑位hole = right;//left從左往右找比基準值大的while (left < right && arr[left] <= key){left++;}//將left位置存放的值拿去填坑arr[hole] = arr[left];//更新坑位hole = left;}//跳出循環，必有left==right，此時left和right都指向坑位hole//而hole就是基準值應該在的位置//用基準值填最后一個坑arr[hole] = key;return hole;
}int _QuickSort_lomuto(int* arr, int left, int right)
{int midi = GetMid(arr, left, right);swap(&arr[midi], &arr[left]);int keyi = left;int prev = left;int pcur = prev + 1;while (pcur <= right){if (arr[pcur] < arr[keyi] && ++prev != pcur){swap(&arr[prev], &arr[pcur]);}pcur++;}//走到最后，prev的位置就是基準值應該存放的位置swap(&arr[prev], &arr[keyi]);return prev;
}//快速排序
//left表示序列的左端點下標  right表示序列的右端點下標
void QuickSort(int* arr, int left, int right)
{if (left >= right)//左端點>=右端點，說明這個序列中已經有序{return;}if (right - left + 1 < 10)//小區間優化，不再遞歸分割排序，減少遞歸次數，直接使用插入排序{//插入排序的第一個參數時待排序列的起始地址，待排序列的區間是[left,right],//所以待排序列的起始地址是arr+leftInsertSort(arr+left, right - left + 1);}else{//找基準值keyiint keyi = _QuickSort_lomuto(arr, left, right);//找到基準值后，將序列劃分：left  keyi   rightQuickSort(arr, left, keyi - 1);QuickSort(arr, keyi + 1, right);}}

快速排序之三路劃分

雖然上面的代碼解決了，但對于下面的情況還是不能達到優化效果：

現在小編就再用前面講的lomuto雙指針法來舉一個例子：假設我們要排序的數組長這樣：{2,2,2,2,2}，如果利用雙指針法，那么遞歸過程中形成的二叉樹的形狀：

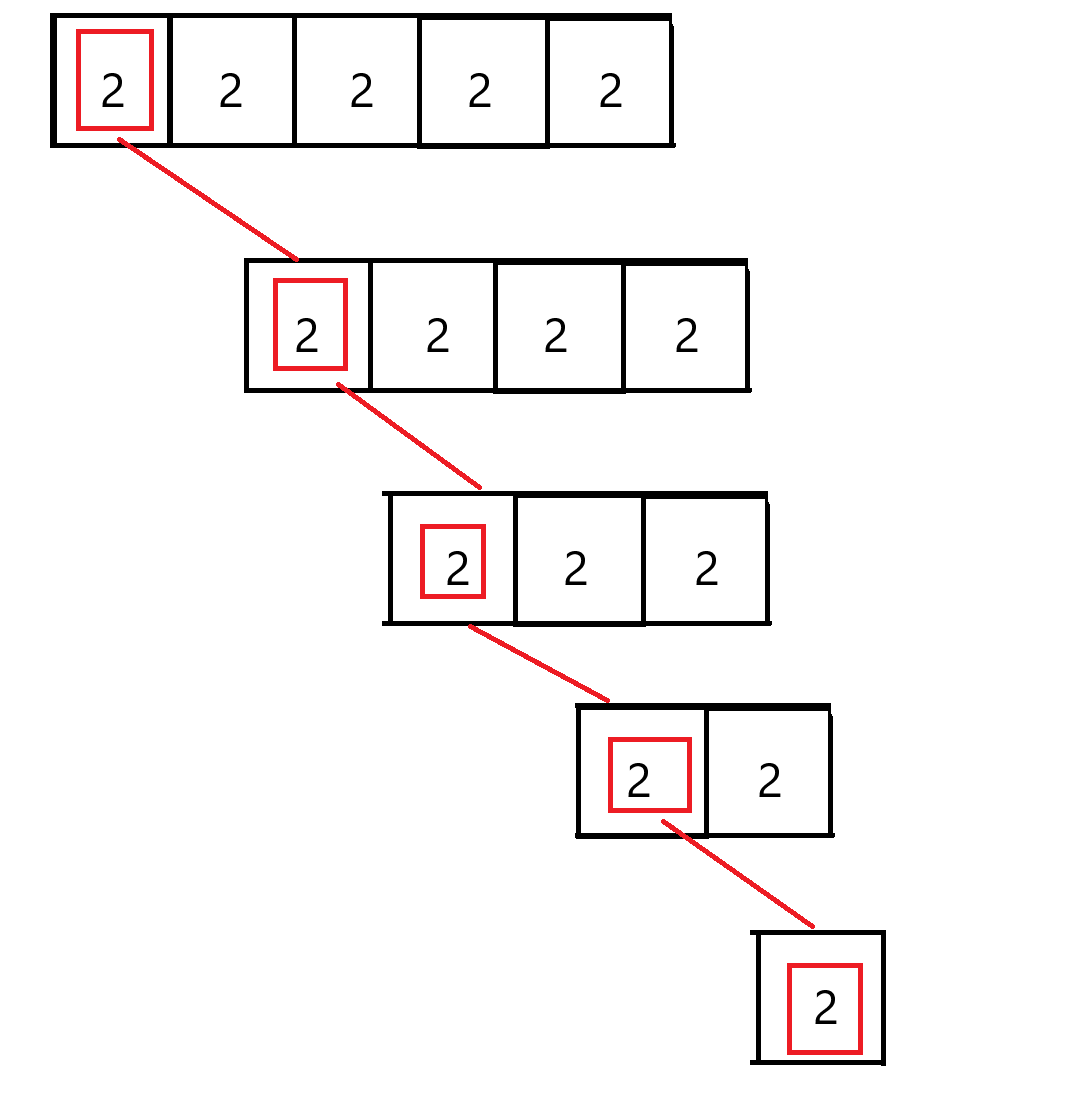
如圖，當數組中都是重復數據時，lomuto雙指針法遞歸產生的二叉樹的深度就會變成n，時間復雜度也就退化成了O(N^2)。

那么，有沒有什么好的解決辦法呢？

既然小編已經提出了，那就一定是有解決辦法的，這就是我們這一部分要學的快排的三路劃分。

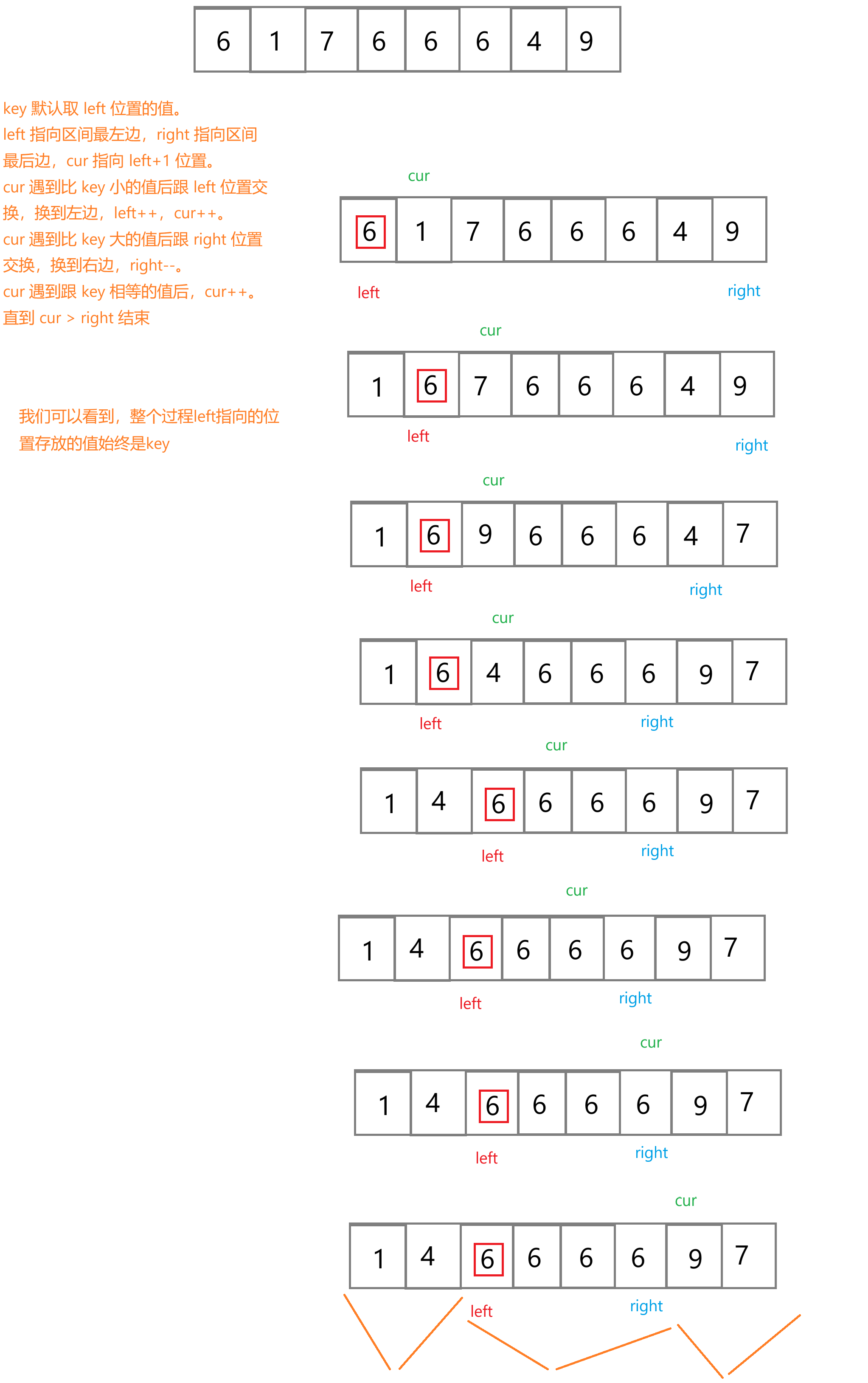
當面對有大量跟 key 相同的值時，三路劃分的核心思想有點類似 hoare 的左右指針和 lomuto 的前后指針的結合。核心思想是把數組中的數據分為三段【比 key 小的值】【跟 key 相等的值】【比 key 大的值】，所以叫做三路劃分算法。

理解一下實現思想：

  1. key 默認取 left 位置的值。
  2. left 指向區間最左邊，right 指向區間最后邊，cur 指向 left+1 位置。
  3. cur 遇到比 key 小的值后跟 left 位置交換，換到左邊，left++，cur++。
  4. cur 遇到比 key 大的值后跟 right 位置交換，換到右邊，right--。
  5. cur 遇到跟 key 相等的值后，cur++。
  6. 直到 cur > right 結束

//三路劃分實現快速排序
void QuickSort_ThreeWay(int* arr, int left, int right)
{if (left >= right){return;}//小區間優化//if (right - left + 1 < 10)//{//	InsertSort(arr + left, right - left + 1);//}//else//{//三路劃分int midi = GetMid(arr, left, right);swap(&arr[midi], &arr[left]);int key = arr[left];int begin = left, end = right;int cur = left + 1;while (cur <= right){if (arr[cur] < key){swap(&arr[cur], &arr[left]);left++;cur++;}else if (arr[cur] > key){swap(&arr[cur], &arr[right]);right--;}else{cur++;}}//將序列分成了三部分：[begin,left-1]  [left,right]  [right+1,end]//[left,right]區間的數值都等于基準值QuickSort_ThreeWay(arr, begin, left - 1);QuickSort_ThreeWay(arr, right + 1, end);//}
}

快速排序之自省排序

introsort 是 introspective sort 采用了縮寫，他的名字其實表達了他的實現思路，他的思路就是進行自我偵測和反省，快排遞歸深度太深（cpp stl 中使用的是深度為 2 倍排序元素數量的對數值）那就說明在這種數據序列下，選 key 出現了問題，性能在快速退化，那么就不要再進行快排分割遞歸了，改換為堆排序進行排序。

自省排序的核心思想是：

  1. 快速排序為主：處理大多數情況

  2. 堆排序為保險：防止快速排序退化

  3. 插入排序優化：處理小數據量

  4. 智能監控：根據實際情況自動切換算法

這種混合方法實現了：

  • ? 保持快速排序的平均性能

  • ? 避免最壞情況下的性能退化

  • ? 對小數據量有優化效果

  • ? 在實際應用中表現穩定

排序的基本思想：

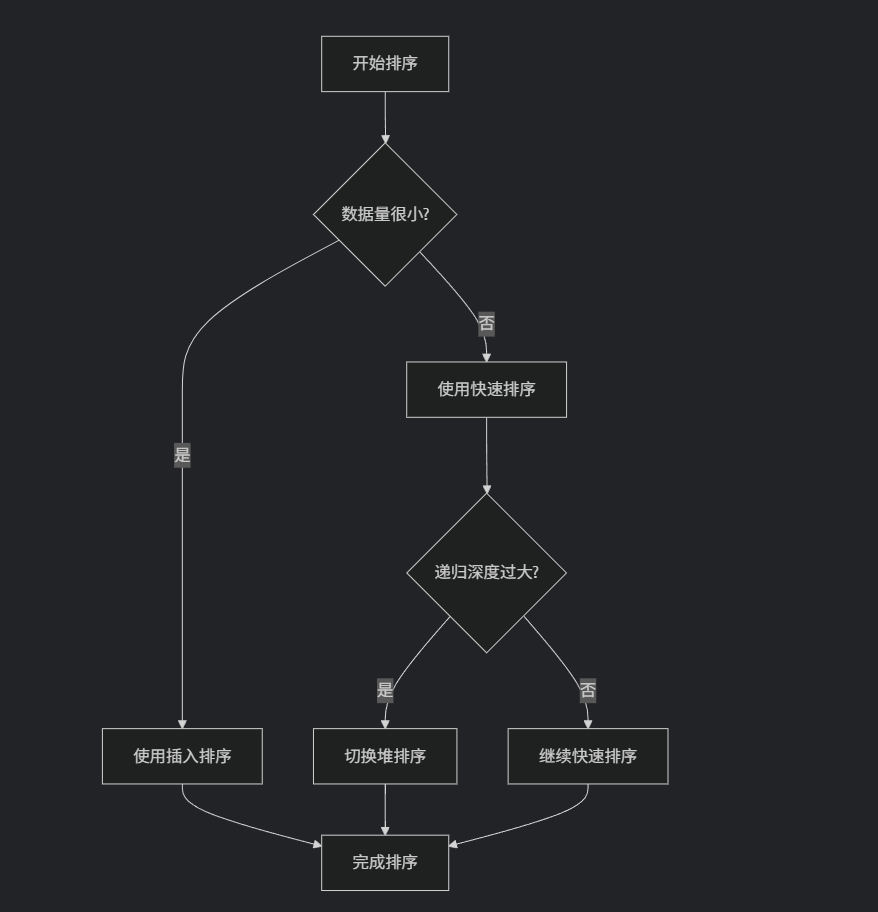
實現代碼：

//自省排序
void IntroSort(int* arr, int left, int right, int depth, int defaltdepth)
{if (left >= right){return;}// 數組?度?于16的?數組，換為插?排序，簡單遞歸次數if (right - left + 1 < 16){InsertSort(arr + left, right - left + 1);return;}//檢查是否遞歸層次太深了if (depth > defaltdepth){HeapSort(arr + left, right - left + 1);return;}depth++;//使用lomuto雙指針法int midi = GetMid(arr, left, right);swap(&arr[left], &arr[midi]);int keyi = left;int prev = left, pcur = prev + 1;while (pcur <= right){if (arr[pcur] < arr[keyi] && ++prev != pcur){swap(&arr[pcur], &arr[prev]);}pcur++;}swap(&arr[keyi], &arr[prev]);keyi = prev;//繼續遞歸左右子序列[left,keyi-1][keyi+1,right]IntroSort(arr, left, keyi - 1, depth, defaltdepth);IntroSort(arr,  keyi +1, right,depth, defaltdepth);
}void  QuickSort_(int* arr, int left, int right)
{int depth = 0;int logN = 0;//表示遞歸深度的閾值int N = right - left + 1;//表示數組元素個數//為什么需要這個logn：//	在自省排序中，當遞歸深度超過 2 × logn 時，算法會從快速排序切換到堆排序//	這是為了防止快速排序在最壞情況下（如已經有序的數組）退化為 O(n2) 的時間復雜度//	通過限制遞歸深度，保證最壞情況下的時間復雜度為 O(n log n)//計算遞歸深度的閾值for (int i = 0; i < N; i *= 2){logN++;}// introspective sort -- ?省排序IntroSort(arr, left, right, depth, 2 * logN);
}

小結：本節內容我們深入探索了快速排序的實現方法，這一節將上一篇文章中快速排序的性能問題逐個擊破，小編覺得這一節是比較有意思的。同時這一小節的代碼量也是超級豐富的，兄弟們一定要自己手動敲一下代碼哦！！！

喜歡小編的兄弟們歡迎三連哦，小編會繼續更新編程方面的內容的。對于本節內容有任何問題的朋友歡迎在評論區留言哦！！！
?

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/bicheng/94265.shtml
繁體地址，請注明出處：http://hk.pswp.cn/bicheng/94265.shtml
英文地址，請注明出處：http://en.pswp.cn/bicheng/94265.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

《遞歸與迭代：從斐波那契到漢諾塔的算法精髓》

《遞歸與迭代：從斐波那契到漢諾塔的算法精髓》

&#x1f525;個人主頁&#xff1a;艾莉絲努力練劍 ?專欄傳送門&#xff1a;《C語言》、《數據結構與算法》、C語言刷題12天IO強訓、LeetCode代碼強化刷題、洛谷刷題、C/C基礎知識知識強化補充、C/C干貨分享&學習過程記錄 &#x1f349;學習方向&#xff1a;C/C方向學習者…
閱讀更多...
《LINUX系統編程》筆記p3

《LINUX系統編程》筆記p3

可重用函數不使用全局部變量&#xff0c;可以重復使用的函數.stat 命令作用&#xff1a;顯示一個文件或文件夾的“元信息”。文件基本信息文件&#xff08;File&#xff09;&#xff1a;顯示所查詢對象的名稱。大小&#xff08;Size&#xff09;&#xff1a;文件的大小&#xf…
閱讀更多...
大模型0基礎開發入門與實踐：第3章 機器的“統計學”：機器學習基礎概念掃盲

大模型0基礎開發入門與實踐：第3章 機器的“統計學”：機器學習基礎概念掃盲

第3章 機器的“統計學”&#xff1a;機器學習基礎概念掃盲 1. 引言 想象一下&#xff0c;你是一位古代的農夫&#xff0c;畢生的經驗告訴你&#xff1a;烏云密布、燕子低飛&#xff0c;那么不久便會下雨。你并沒有學習過氣象學&#xff0c;也不懂大氣壓和水汽凝結的原理。你的“…
閱讀更多...
Java調用Ollama（curl方式）

Java調用Ollama（curl方式）

1. 安裝Ollama Search 2. 調用 相關依賴 <dependencies><dependency><groupId>org.apache.httpcomponents</groupId><artifactId>httpclient</artifactId><version>4.5.14</version></dependency><dependency>&…
閱讀更多...
nodejs koa框架使用

nodejs koa框架使用

1: KOA 是express 打造的下一代web 開發框架提供更小更強的的核心功能&#xff0c;通過Promise 、async/await 進行異步編程&#xff0c;koa 可以不使用回調&#xff0c;解決了回調地獄的問題 blueBird 是nodejs 最出名的Primise 實現&#xff0c;除了實現標準的promise 之外&a…
閱讀更多...
2025年圖像處理與光學國際會議（ICIPO 2025）

2025年圖像處理與光學國際會議（ICIPO 2025）

2025年圖像處理與光學國際會議&#xff08;ICIPO 2025&#xff09; 2025 International Conference on Image Processing and Optics一、大會信息會議簡稱&#xff1a;ICIPO 2025 大會地點&#xff1a;中國北京 審稿通知&#xff1a;投稿后2-3日內通知 投稿郵箱&#xff1a;iac…
閱讀更多...
Kubernetes 構建高可用、高性能 Redis 集群

Kubernetes 構建高可用、高性能 Redis 集群

k8s下搭建Redis高可用1. 部署redis服務創建ConfigMap創建 Redis創建 k8s 集群外部2. 創建 Redis 集群自動創建 redis 集群手動創建 redis 集群驗證集群狀態3. 集群功能測試壓力測試故障切換測試4. 安裝管理客戶端編輯資源清單部署 RedisInsight控制臺初始化控制臺概覽實戰環境使…
閱讀更多...
文件IO的基礎操作

文件IO的基礎操作

Java針對文件進行的操作:文件系統操作,File類(file類指定的路徑,可以是一個不存在的文件)文件內容操作 : 流對象分為兩類(1)字節流 以字節為基本的讀寫單位的 二進制文件 InputStream OutputStream(2)字符流 以字符為基本的讀寫單位的 …
閱讀更多...
【模版匹配】基于深度學習

【模版匹配】基于深度學習

基于深度學習的模版匹配 概述 本報告整理了2024-2025年最新的、可直接使用的模板匹配相關論文、方法和開源代碼實現。所有方法都提供了完整的代碼實現和預訓練模型&#xff0c;可以直接應用到實際項目中。 一、輕量級現代模板匹配框架 1.1 UMatcher - 4M參數的緊湊型模板匹…
閱讀更多...
CMake進階：Ninja環境搭建與加速項目構建

CMake進階：Ninja環境搭建與加速項目構建

目錄 1.引入Ninja的原因 2.Ninja 環境搭建&#xff08;跨平臺&#xff09; 2.1.Linux系統安裝 2.2.macOS 系統 2.3.Windows 系統 2.4.源碼編譯安裝&#xff08;通用方案&#xff09; 3.Ninja 與構建系統配合&#xff1a;以 CMake 為例 4.加速構建的關鍵技巧 5.Ninja 與…
閱讀更多...
開發避坑指南(35)：mybaits if標簽test條件判斷等號=解析異常解決方案

開發避坑指南(35)：mybaits if標簽test條件判斷等號=解析異常解決方案

異常信息 org.mybatis.spring.MyBatisSystemException: nested exception is org.apache.ibatis.builder.BuilderException: The expression orderInfo.idList evaluated to a null value.報錯語句 <if test"orderInfo.queryFlag ! null and orderInfo.queryFlag sett…
閱讀更多...
GitCode 疑難問題診療：全面指南與解決方案

GitCode 疑難問題診療：全面指南與解決方案

引言 在軟件開發的動態領域中&#xff0c;GitCode 作為一款強大的分布式版本控制系統&#xff0c;已然成為團隊協作與項目管理的基石。它賦予開發者高效管理代碼版本、輕松實現并行開發以及順暢協同合作的能力。然而&#xff0c;如同任何復雜的技術工具&#xff0c;在 GitCode…
閱讀更多...
使用 JS 渲染頁面并導出為PDF 常見問題與修復

使用 JS 渲染頁面并導出為PDF 常見問題與修復

本文直擊兩個最常見的導出痛點&#xff0c;并給出可直接落地的診斷 修復方案&#xff08;適用于 html2canvas jsPDF ECharts/自繪 canvas 場景&#xff09;。 問題清單 問題 A&#xff1a;導出后圖表模糊&#xff0c;線條與文字不清晰&#xff08;低分辨率&#xff09;。問題…
閱讀更多...
【Java后端】【可直接落地的 Redis 分布式鎖實現】

【Java后端】【可直接落地的 Redis 分布式鎖實現】

可直接落地的 Redis 分布式鎖實現&#xff1a;包含最小可用版、生產可用版&#xff08;帶 Lua 原子解鎖、續期“看門狗”、自旋等待、可重入&#xff09;、以及基于注解AOP 的無侵入用法&#xff0c;最后還給出 Redisson 方案對比與踩坑清單。一、設計目標與約束 獲取鎖&#x…
閱讀更多...
數據結構 -- 鏈表--雙向鏈表的特點、操作函數

數據結構 -- 鏈表--雙向鏈表的特點、操作函數

雙向鏈表的操作函數DouLink.c#include "DouLink.h" #include <stdio.h> #include <stdlib.h> #include <string.h>/*** brief 創建一個空的雙向鏈表* * 動態分配雙向鏈表管理結構的內存&#xff0c;并初始化頭指針和節點計數* * return 成功返回指…
閱讀更多...
Wireshark獲取數據傳輸的碼元速率

Wireshark獲取數據傳輸的碼元速率

一、Wireshark的物理層參數 Wireshark主界面可以看到數據發送時刻和長度&#xff1a; 這個時刻是Wireshark完整獲取數據包的時刻&#xff0c;實際上就是結束時刻。 需要知道的是&#xff1a; Wireshark工作在數據鏈路層及以上&#xff0c;它能解碼 以太網幀 / IP 包 / TCP…
閱讀更多...
11.1.3 完善注冊登錄，實現文件上傳和展示

11.1.3 完善注冊登錄，實現文件上傳和展示

1、完善注冊/登錄 1. 涉及的數據庫表單&#xff1a;user_info 2. 引用MySQL線程池&#xff0c;Redis線程池 3. 完善注冊功能 4. 完善登錄功能 2.1 涉及的數據庫表單&#xff1a;user_info 重新創建數據庫 #創建數據庫 DROP DATABASE IF EXISTS 0voice_tuchuang;CREATE D…
閱讀更多...
【Linux文件系統】目錄結構

【Linux文件系統】目錄結構

有沒有剛進入Linux世界時&#xff0c;對著黑乎乎的終端&#xff0c;輸入一個 ls / 后&#xff0c;看著蹦出來的一堆名字 like bin, etc, usr&#xff0c;感覺一頭霧水&#xff0c;像是在看天書&#xff1f; 別擔心&#xff0c;你不是一個人。Linux的文件系統就像一個超級有條理…
閱讀更多...
螺旋槽曲面方程的數學建模與偏導數求解

螺旋槽曲面方程的數學建模與偏導數求解

螺旋槽曲面的數學描述 在鉆頭設計和機械加工領域，螺旋槽的幾何建模至關重要。螺旋槽通常由徑向截形繞軸做螺旋運動形成，其數學模型可通過參數方程和隱函數方程兩種方式描述。 設螺旋槽的徑向截形方程為： y=f(z)y = f(z)y=f(z) x=xcx = x_cx=xc? 其中 xcx_cxc? 為常數，…
閱讀更多...
線性回歸：機器學習中的基石

線性回歸：機器學習中的基石

在機器學習的眾多算法中&#xff0c;線性回歸無疑是最基礎也是最常被提及的一種。它不僅在統計學中占有重要地位&#xff0c;而且在預測分析和數據建模中也發揮著關鍵作用。本文將深入探討線性回歸的基本概念、評估指標以及在實際問題中的應用&#xff0c;并通過一個模擬的氣象…
閱讀更多...
最新文章

Copyright @ 2022~2023