【數據結構】第一講 —— 概論
文章目錄
- 【數據結構】第一講 —— 概論
- 1.1 基本概念和常用術語
- 1.2 了解數據結構
- 1. 數據結構
- 2. 數據的邏輯結構
- 3. 數據的物理結構(存儲結構)
- 4. 數據的運算
- 1.3 算法的描述和分析
- 1.3.1 算法的描述
- 1.3.2
1.1 基本概念和常用術語
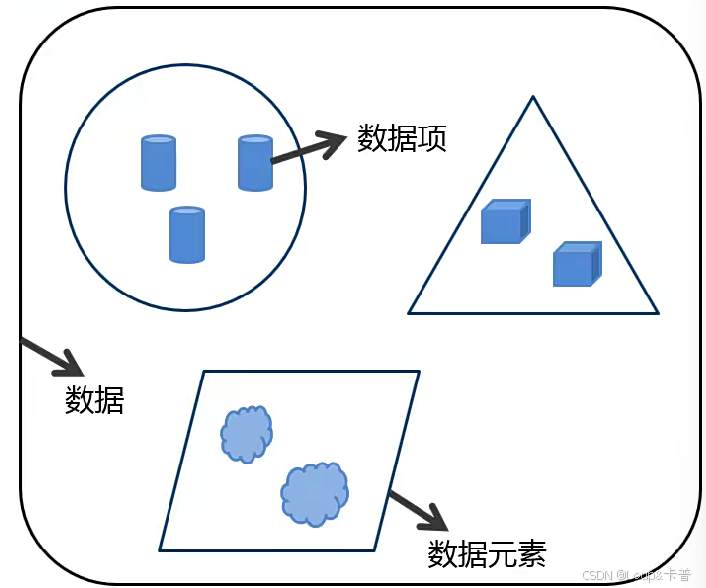
- 數據的基本單位是數據元素,最小單位是數據項
- 一個數據元素可以由若干個數據項組成
1.2 了解數據結構
1. 數據結構
定義:數據結構指的是數據元素之間的相互關系,即數據的組織形式
內容:數據的邏輯結構、數據的存儲結構、數據的運算
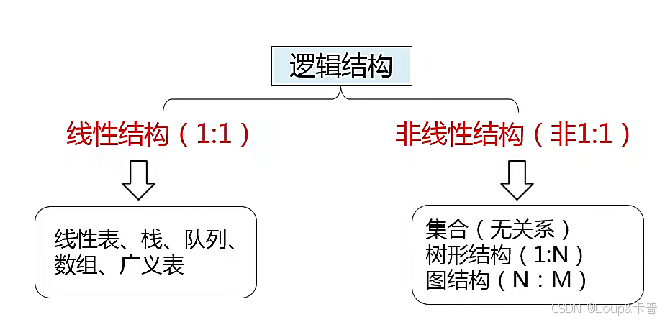
2. 數據的邏輯結構
定義:從邏輯關系上描述數據,與數據元素的存儲結構無關,獨立于計算機
分類:線性結構和非線性結構
3. 數據的物理結構(存儲結構)
定義:數據元素及其關系在計算機內的存儲方式,稱為數據的存儲結構
實現方法:順序存儲、鏈接存儲、索引存儲、散列存儲

4. 數據的運算
定義:對數據元素施加的操作(行為)
內容:最常用的插入、刪除、查找、排序等。
插入:增加節點、入棧、入隊
刪除:刪除節點、出棧、出隊
查找:二分查找、散列查找
排序:選擇排序、快速排序
1.3 算法的描述和分析
1.3.1 算法的描述

算法是對特定問題的求解方法(步驟)的一種描述,是指令的有限序列,其中每一條指令表示一個或多個操作
算法的五大基本準則:
- 有窮性:一個算法必須總是在執行有窮步之后結束,且每一步都在有窮時間內完成。
- 確定性:算法中每一條指令必須由確切的含義,不存在二義性
- 可行性:一個算法是能行的。即算法描述的操作都可以通過已經實現的基本運算執行有限次來實現。
- 輸入:一個算法有零個或多個輸入,這些輸入取自于某個特定的對象集合
- 輸出:一個算法有一個或多個輸出,這些輸出是同輸入有著某些特定關系的量
1.3.2
算法的分析因素
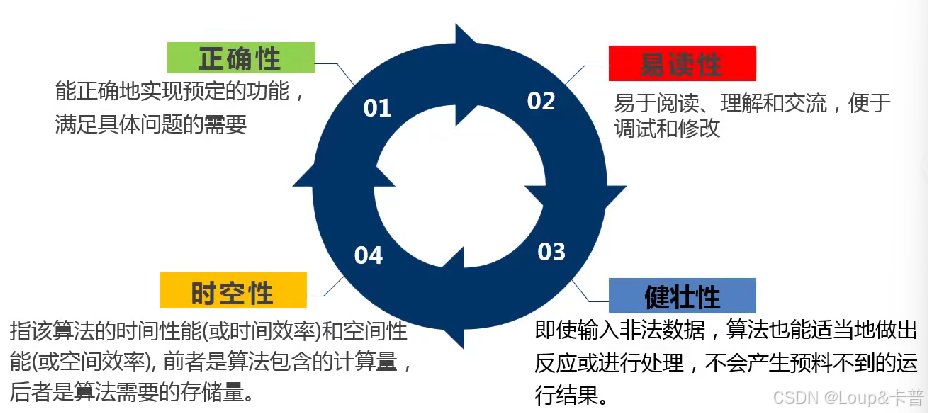
健壯性又叫魯棒性
時間復雜度:
算法中基本操作重復執行的次數是問題規模n的某個函數,其時間量度記作T(n) = O(f(n)) ,稱作算法的漸進時間復雜度(Asymptotic Time complexity),簡稱時間復雜度。
一般地,常用最深層循環內地語句中原操作地執行頻度(重復執行地次數)來表示。
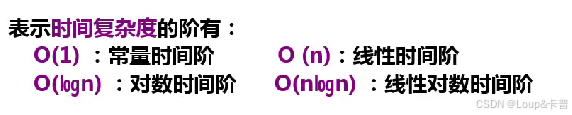
for (i = 1; i <= n; ++i) {++x;s+=x;
}
時間復雜度為:O(n) ,即為線性階
for (i = 1; i <= n; ++i) {for (j = 1; j <= n; ++j) {++x; s+=x}
}
時間復雜度為:O(n^2) ,即平方階
for (i = 1; i <= n; ++i) {for (j = 1; j <= n; ++j) {c[i][j] = 0;for (k = 1; k <= n; ++k) {c[i][j] += a[i][k] * b[k][j];}}
}
需要注意其中 c[i][j] = 0 不能納入計算時間復雜度的語句。需要計算最深層循環c[i][j] += a[i][k] * b[k][j]; 的語句。
時間復雜度為:O(n^3) ,即為立方階
空間復雜度
空間復雜度是指算法編寫成程序后,在計算機中運行時所需存儲空間大小的度量,該存儲空間一般包括三個方面:
- 指令常數變量所占用的存儲空間;
- 輸入數據所占用的存儲空間;
- 輔助(存儲)空間。
一般地,算法的空間復雜度指的是輔助空間

——CRUD基礎)


)








)



![[Python] -項目實戰7- 用Python和Tkinter做一個圖形界面小游戲](http://pic.xiahunao.cn/[Python] -項目實戰7- 用Python和Tkinter做一個圖形界面小游戲)
+ OpenCV 顯示圖片的3種方法)

