f ( x ) = π 2 ? ∣ x ∣ f(x)=\frac{\pi}{2}-|x| f(x)=2π??∣x∣
由于是偶函數只需要求 cos ? ( n x ) , 1 \cos(nx),1 cos(nx),1 的系數
a n = 0 a_n= 0 an?=0, n n n 是偶數
a n = 1 ( 2 n ? 1 ) 2 a_n= \frac{1}{(2n-1)^2} an?=(2n?1)21?, n n n 是奇數
則 f ( x ) = ∑ k = 1 ∞ 1 ( 2 n ? 1 ) 2 cos ? ( ( 2 k ? 1 ) x ) f(x)= \sum_{k=1}^\infty \frac{1}{(2n-1)^2} \cos((2k-1)x) f(x)=∑k=1∞?(2n?1)21?cos((2k?1)x).
圖示如下,隨著階數 k k k 的增加,級數逼近原函數。
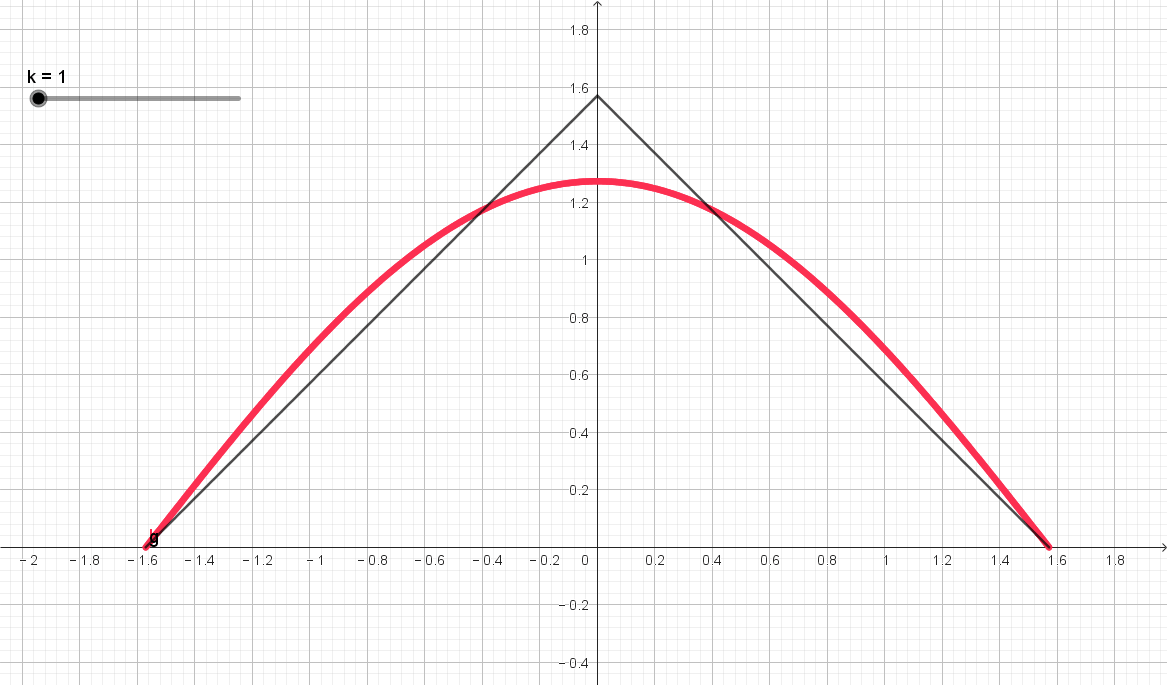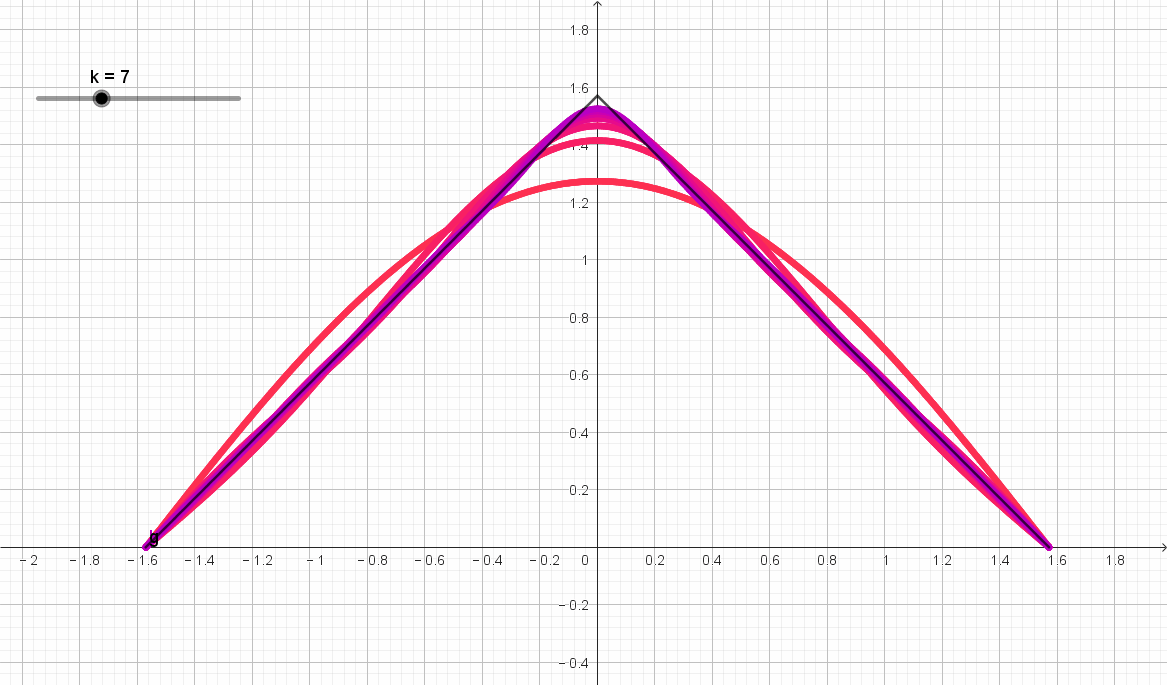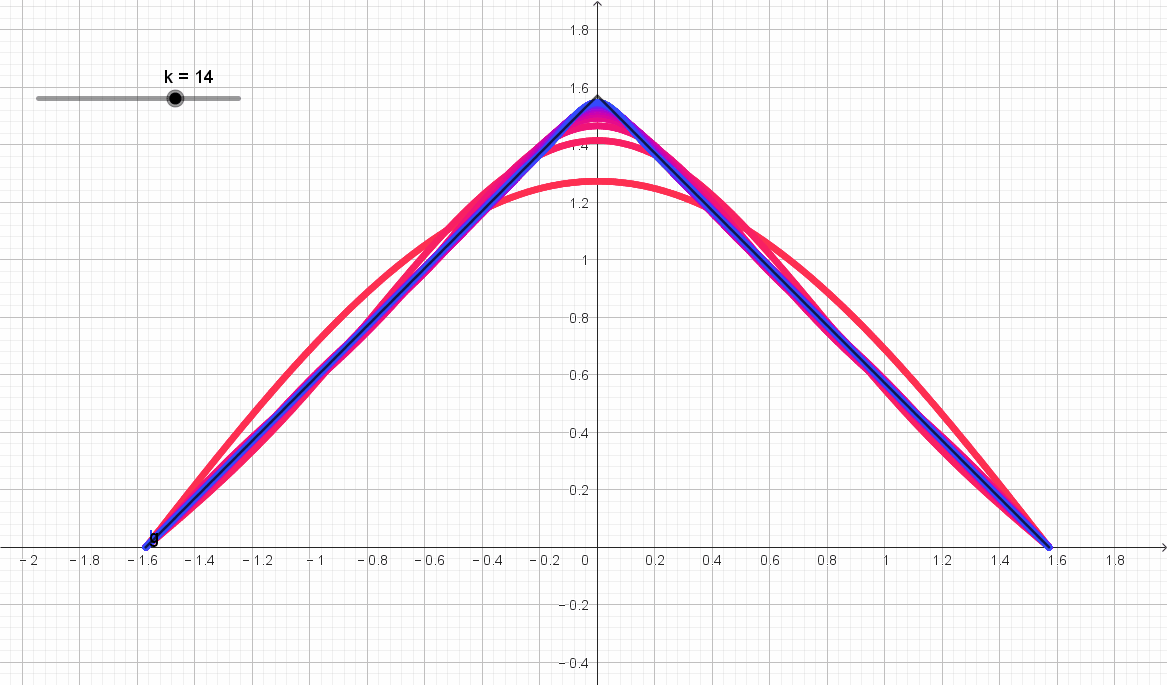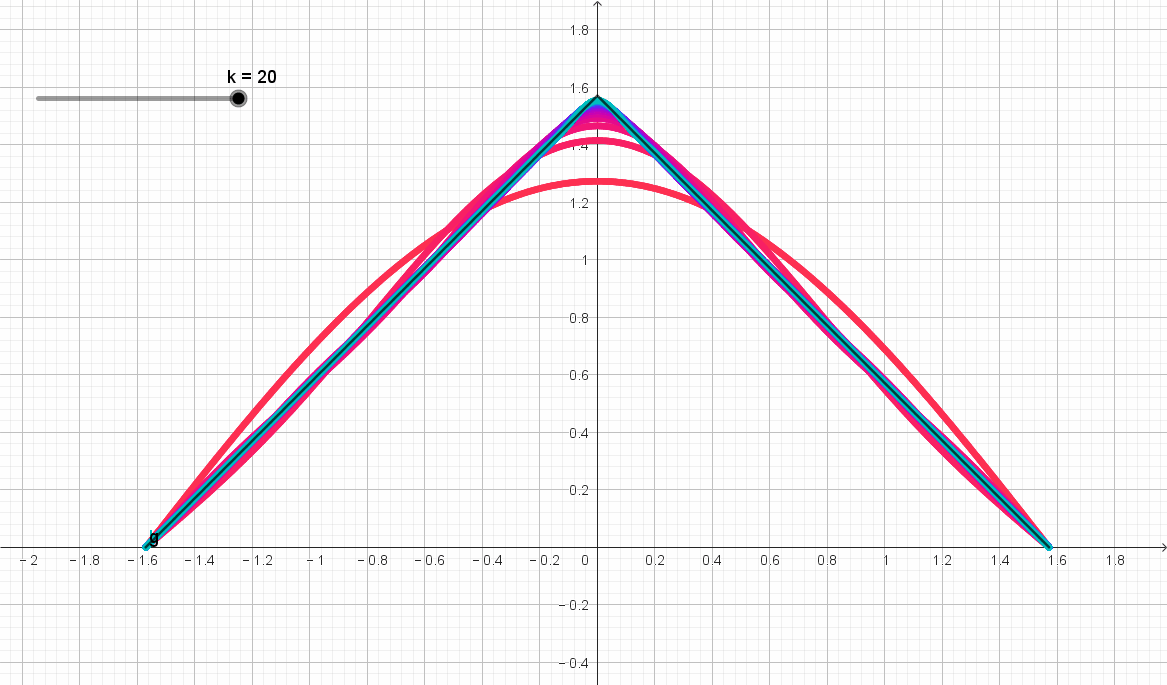







)



)







