數學基礎

向量

點乘，叉乘和投影：

插值

三角形插值

**重心坐標：**我們通過任意點的重心坐標來插值。$V=\alpha V_A+\beta V_B+\gamma V_C$。注意重心坐標沒有投影不變性，如果插值三維屬性，需要利用投影前的坐標插值。例如深度插值應該用三維空間坐標。

雙線性插值

平面定義

法線-點表示

第一部分：光柵化

坐標變換

二維變換

從上述公式中我們發現，平移變換需要兩個向量的加和，為了使得所有的變換統一寫成矩陣乘法的形式，我們引入齊次坐標。在齊次坐標中，每個點表示為：$(x,y,1{)}^{\mathrm{T}}$,每個向量表示為：$(x,y,0{)}^{\mathrm{T}}$。通過這種方式我們可以確保，點加點等于點（中點），點減點等于向量，向量加減向量還是向量。點加減向量還是向量。特別地，我們認為$(x,y,k{)}^{\mathrm{T}}=(x/k,y/k,1{)}^{\mathrm{T}}$。在引入齊次坐標后，平移可以寫成：

在其次坐標系下的變化矩陣最后一行一般都是001，左上角是縮放，拉伸，鏡像，旋轉變化，最后一列是平移變換。在這種情況下，是先進性二維變換，在進行平移變換。

如果要求逆變換，求矩陣的逆即可。由于矩陣乘積不滿足交換律，因此計算的時候不可更改變換矩陣的順序。注意旋轉矩陣是正交矩陣，求旋轉矩陣的逆相當于求旋轉矩陣的轉置。

3D變換

在三位空間中點和向量的描述形式和二維空間類似（只增加了一個z維）。三位空間中的旋轉和二位空間有些許不同。我們按照xyz的順序構建坐標系，沿x軸旋轉的時候yxz是x軸，沿y軸旋轉的時候xz是-y軸。因此需要添加符號（conx=-conx）

我們可以通過分解的方式，吧沿任意軸旋轉a度分解為沿xyz軸分別旋轉a1,b1,c1度。也可以通過三位旋轉矩陣直接求沿著任意軸旋轉。$R(n,\alpha )$是沿著空間中任意一個軸n逆時針旋轉$\alpha$度后的結果。

視圖變換（MVP）

投影變換

投影變換分為兩種：正交投影和透視投影。正交投影我們先做平移，再做縮放。我們把物體的中心移動到坐標軸遠點，之后把物體限制在（-1，1）的立方體中。

**透視投影：**我們先把透視投影變換為正交投影所需的長方體，再進行正交投影。再壓縮透視投影的梯形體時，對于前面的面上的點，z值不變，后面面上的點同理。

光柵化

采樣

我們先忽略z軸，考慮-1，1的正方體。采樣就是判斷像素點是否在三角形內。我們可以對整個屏幕范圍采樣，也可以采用bounding采樣，還有行bounding采樣。

抗鋸齒（反走樣）

可見性（遮擋）

如何在采樣的時候維持正確的模型順序？–深度緩沖方法。該方法無法處理透明物體。如果兩個三角形在同一個像素內有相同的深度如何處理？（工程實現問題）

外鏈圖片轉存失敗,源站可能有防盜鏈機制,建議將圖片保存下來直接上傳

著色與紋理

著色器可以做任何事情！！！

在本章節，我們只考慮著色點本身，不考慮其他點（比如遮擋）。每個著色點可以是一個像素，也可以是一個fragment，這取決于我們如何采樣。I表示入色光的單位光強，V代表反色方向，n是法線。ivn都是單位向量。

外鏈圖片轉存失敗,源站可能有防盜鏈機制,建議將圖片保存下來直接上傳

Blinn-Phong著色模型

該模型是一個經驗模型。在該模型中，我們考慮漫反射，鏡面反色和環境光。

漫反射diffuse：$L_d=k_d(I/r^2)max(0,nI)$。其中kd為漫反射系數（物體顏色），nI是光線和著色點的cos值。

鏡面反射specular：$L_s=k_s(L/r^2)max(0,nh{)}^p,,,h=(v+I)/||V+I||$，H代表入i和v的半程向量，如果該半程向量與n很近，則代表人眼看到的高光越明顯（為什么算半程向量，而不是算光的反色向量和人眼向量的sin，是因為半程向量計算簡單）ks一般為白色。

環境光ambient:$L_a=K_a{I}_a$，該模型是一個經驗模型，環境光當作一個常熟項簡單處理。

最終著色：$L_d+L_s+L_a$

著色頻率

1. 三角形著色，三角形法線可以用叉乘計算
2. 頂點著色，頂點法線可以用該頂點相關的三角形的法線的加權平均值。此外也可以用該頂點實際表示的圖形來確定法線，例如如果用三角形組合表示圓，則頂點的法線防線可能是圓心到該頂點的連線方向。
3. 像素著色（fragemt），算出三角形的所有頂點法線，用插值方法得到像素法線。phong shadings

渲染管線

外鏈圖片轉存失敗,源站可能有防盜鏈機制,建議將圖片保存下來直接上傳

紋理

物體不同位置可能有不同的屬性（著色時用特有的屬性而不用同一的屬性），該屬性定義在物體表面上。我們把這個屬性用一張圖（紋理圖）來表示，同時給出模型上每一個點對應紋理圖上的點（紋理映射，紋理坐標一般定義在三角形的頂點上）。

**紋理太小：**映射道德如果是紋理中的非整數坐標，我們可以采用該頂點周圍的四個點進行雙線性插值，用差值，返回插值后的屬性。

**紋理太大：**紋理太大時會導致采樣頻率不足，從而產生走樣。不同像素覆蓋紋理的區域不同，有些點可能實際覆蓋了很大一部分紋理區域，只返回該點的屬性必然會導致走樣問題。可以通過范圍查詢方法MipMap來緩解。范圍查詢返回一定范圍內的平均值，MipMap是一種近似方法，fast,approx，square。該方法在遠距離下會導致過度模糊。

MipMpa方法

該方法會提前計算4和1，8和1，，，，點的平均值，并保存$lo{g}_{2}h$個紋理圖。其中h是正方形紋理的長度。

在進行紋理映射時，我們首先確定每個點所覆蓋的紋理范圍。我們通過該點周圍的四個點的坐標來把紋理覆蓋范圍近似成正方形。通過紋理覆蓋范圍的邊長查找相應層級的紋理圖。如果log2L不為整數，我們可以在兩層紋理圖中采用三線性插值的方式得到最終屬性。

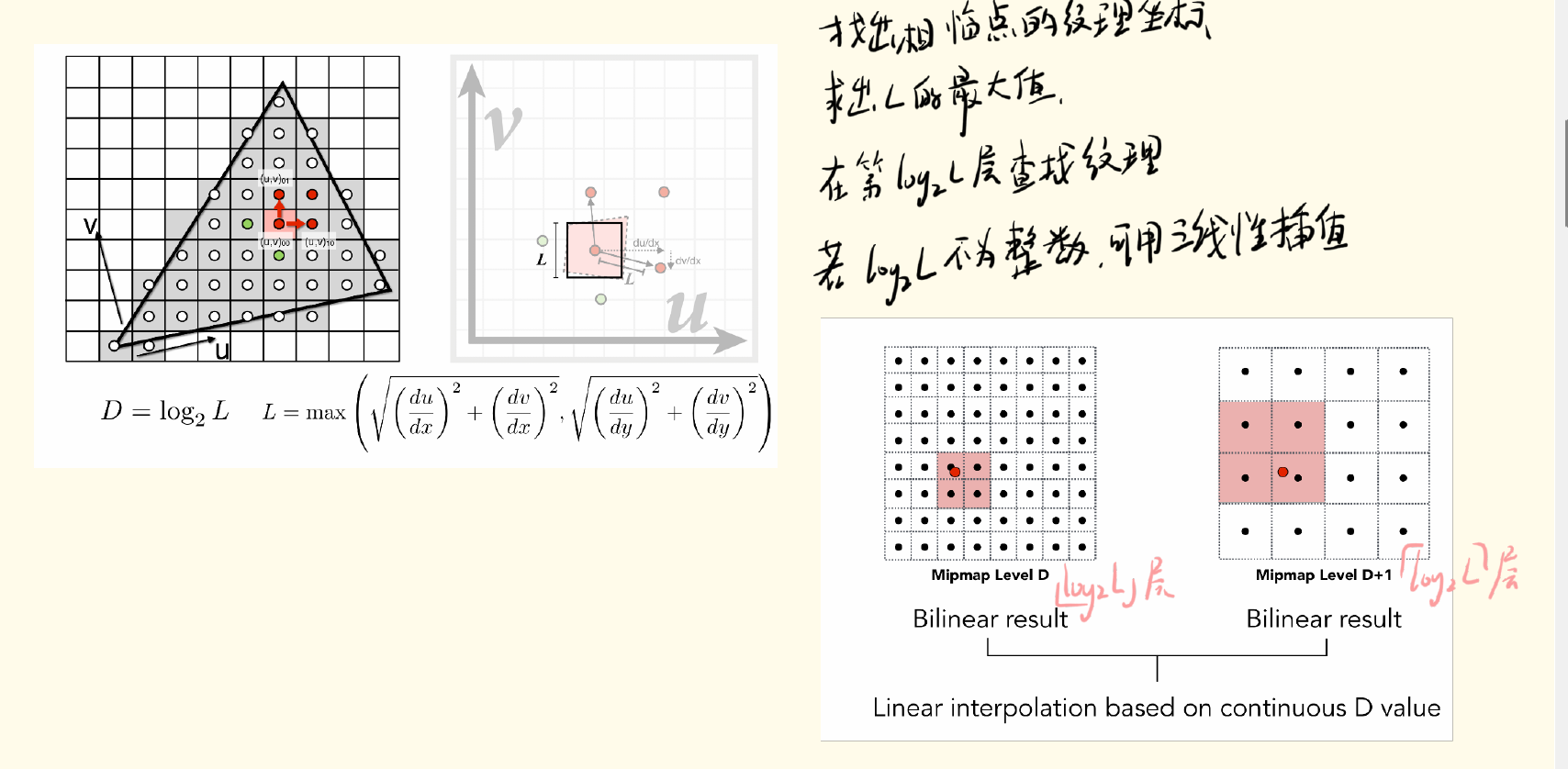
MipMap方法無法解決該點所覆蓋的紋理是矩形（尤其是長條矩形）情況下的的走樣問題。一種緩解方法是各向異性過濾。該方維護不同長寬比例下的紋理分層圖。

如果要緩解傾斜矩形，可以采用EWA filtering方法，但是該方法計算量大。

紋理作用

**環境光紋理：**紋理可認為是gpu中的一塊數據，可以做點查詢和范圍查詢。因此我們可以把環境光做成紋理，渲染過程中通過紋理映射仿照環境光。我們可以用一個光滑的球體來記錄環境光，把球展開貼到環境中的物體表面。用球有個缺點是極點初會被壓縮。為了解決這個問題，我們可以用一個正方體包圍一個球體。把球體上的每一個點都沿著法線方向打到立方體表面。

**凹凸貼圖：**凹凸貼圖定義了每個點的相對移動距離，從而改變著色點的法線，渲染出一種凹凸的質感。實際上該點并不會凹凸。我們假設原始表面是水平，并且法線向上。在二維情況下更改后的法線如下圖左圖。我們通過推廣，可以得到三位空間下更改后的法線，下圖右圖。（紋理保存的是高度變化信息h）。注意在三位空間中，法線方向不一定為001,此時我們需要轉換坐標系，在新的坐標系下法線方向為001，此時我們求出新坐標系下更改后的法線，再將該法線映射會原坐標系。

**三維紋理：**我們也可以定義一個三維空間的噪聲函數來作為紋理。

外鏈圖片轉存失敗,源站可能有防盜鏈機制,建議將圖片保存下來直接上傳

**環境光遮蔽紋理：**我們可以提前算出物體的環境光遮蔽，把他保存為紋理，加速實時渲染。