注:本文以排升序為例
常見的排序算法:

目錄:
一 直接插入排序:
1.1 基本思想:
1.2 代碼:
1.3 復雜度:
二 希爾排序(直接插入排序的優化):
2.1 基本思想:
2.2 代碼:
2.3 復雜度:
三 直接選擇排序:
3.1 基本思想:
3.2 代碼:
3.3 復雜度:
四 堆排序:
一 直接插入排序:
1.1 基本思想:
直接插入排序是?種簡單的插入排序法,其基本思想是:把待排序的記錄按其關鍵碼值的大小逐個插入到?個已經排好序的有序序列中,直到所有的記錄插入完為止,得到?個新的有序序列。
- 實際我們玩撲克牌時就用到了這一思想

動圖:
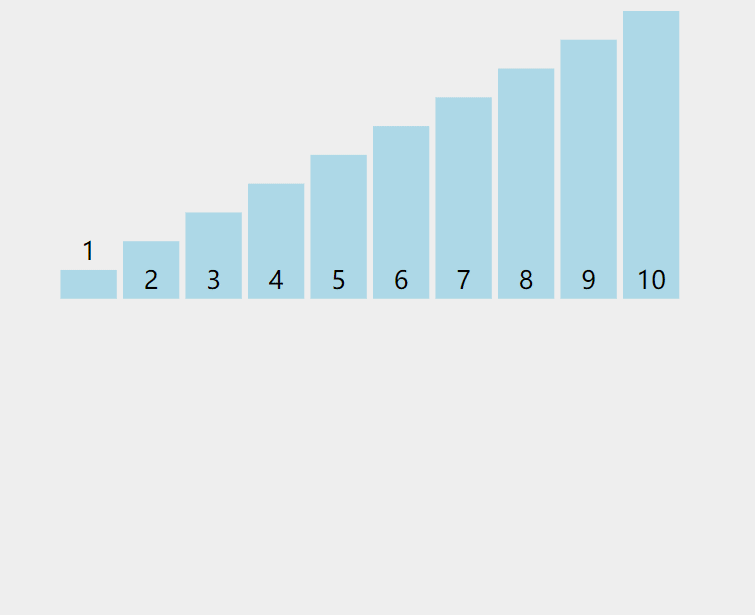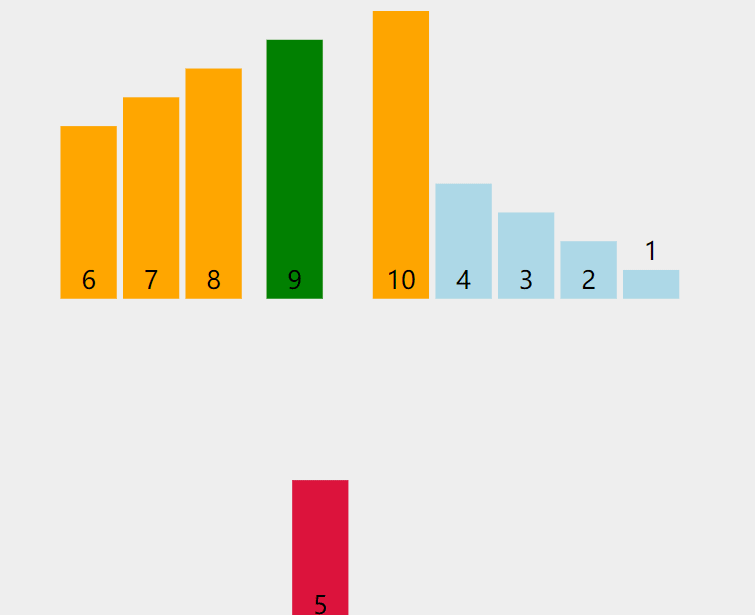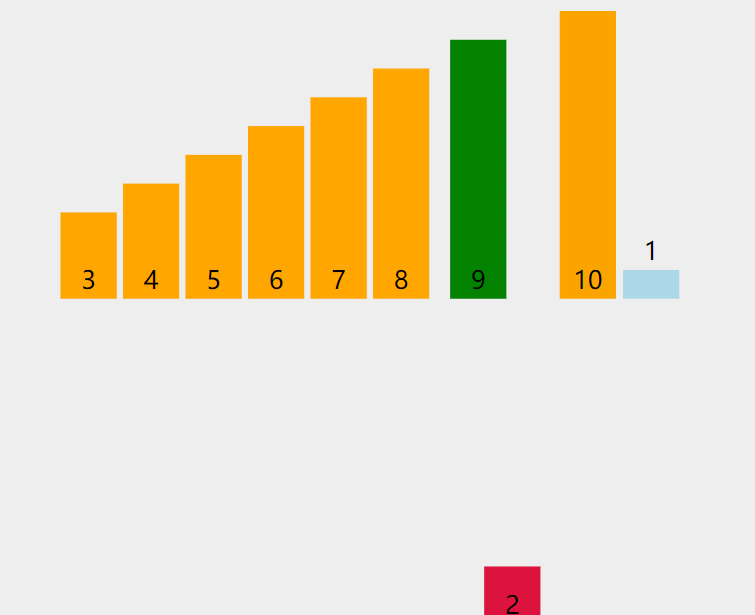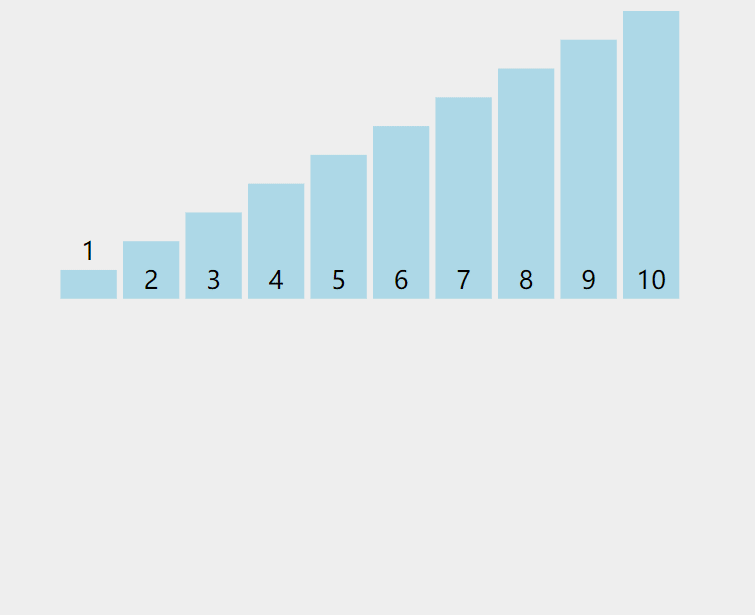
解釋:當插入第 i(i>=1) 個元素時,前面的 array[0],array[1],…,array[i-1] 已經排好序,此時? array[i] 的排序碼與 array[i-1],array[i-2],… 的排序碼順序進行比較,找到插入位置即將 array[i] 插入,原來位置上的元素順序后移。
1.2 代碼:
//直接插入排序
void InsertSort(int* arr, int n)
{for (int i = 0; i < n-1; i++){int end = i;int tmp = arr[end + 1];while (end >= 0){if (arr[end] > tmp){arr[end + 1] = arr[end];end--;}else{break;}}arr[end + 1] = tmp;}
}end:指向有序序列的最后一個數據:初始為0,末態為n-2
tmp:有序序列后的第一個待排序數據:初始為1,末態為n-1
以一次循環為例:
將tmp與end位置數據進行比較,??? 若end處更大,將end位置數據移到end+1處,end--,繼續讓end-1處數據與tmp比較
??? 否則直接跳出循環,此時end+1位置為空,需要放入tmp最壞的情況:當end為0處數據移到end為1處,此時end變為-1,需要跳出循環,并將tmp放到0處
1.3 復雜度:
元素集合越接近有序,直接插入排序算法的時間效率越高。
1.時間復雜度:O(N^2)
2.空間復雜度:O(1)
二 希爾排序(直接插入排序的優化):
在直接插入排序中我們發現,元素越無序,直接插入排序算法時間效率越低(因為比較次數越多)。特別是當數組為降序,我們要排升序,此時數組的相對無序程度達到了最大,時間復雜度也到了最大。所以D.L.Shell在1959年提出了希爾排序。
希爾排序是基于插入排序的以下兩點性質而提出改進方法的:
????????插入排序在對幾乎已經排好序的數據操作時,效率高,即可以達到線性排序的效率。
????????但插入排序一般來說是低效的,因為插入排序每次只能將數據移動一位。
2.1 基本思想:
????????希爾排序法又稱縮小增量法。希爾排序法的基本思想是:先選定?個整數(通常是gap=n/3+1),把 待排序?件所有記錄分成各組,所有的距離相等的記錄分在同?組內,并對每?組內的記錄進?排序,然后gap=gap/3+1得到下?個整數,再將數組分成各組,進行插入排序,當gap=1時,就相當于 直接插入排序。它是在直接插入排序算法的基礎上進行改進?來的,綜合來說它的效率肯定是要?于直接插入排序算法的。
以排序數組為例:

2.2 代碼:
//希爾排序
//希爾排序時間復雜度大約為:O(n^1.3)
void ShellSort(int* arr, int n)
{int gap = n;//6while (gap > 1){gap = gap / 3 + 1;//保證最后一次gap一定為1for (int i = 0; i < n - gap; i++){int end = i;//n-gap-1int tmp = arr[end + gap];while (end >= 0){if (arr[end] > tmp){arr[end + gap] = arr[end];end -= gap;}else {break;}}arr[end + gap] = tmp;}}
}直接插入排序法的改進,其在許多地方有相似之處:
??? 一次預排序
??????? 從下標為0的元素開始,每隔gap-1個數據取數據分到一組,從取數據的方式我們可以得出以下結論:
??????????? 總共有gap組(0-(gap-1)的元素為每一組的頭元素)
??????????? 每組有n/gap或n/gap+1個數據
??????? 每一次排序我們排的是end和end+gap(即tmp)處的元素,保證每次排序都是在同一組內排
??? end初始為0可得tmp初始為gap,tmp末態為n-1可得end末態為n-1-gap
??? 在一組內進行的是直接插入排序,只不過把距離從1換為gap,全部換一下就行了,思路是一樣的,每次預排序結束后,讓gap/3+1,加一保證最后一次排序gap為1,否則無法保證最后一次是直接插入排序
2.3 復雜度:
1.時間復雜度:最好O(N^1.3),最壞O(N^2)
2.空間復雜度:O(1)
三 直接選擇排序:
3.1 基本思想:
1.在元素集合 array[i]–array[n-1] 中選擇關鍵碼最大(小)的數據元素
2.若它不是這組元素中的最后一個(第?個)元素,則將它與這組元素中的最后?個(第?個)元素交換
3.在剩余的 array[i]–array[n-2](array[i+1]–array[n-1]) 集合中,重復上述步驟,直到集合剩余1個元素
動圖:
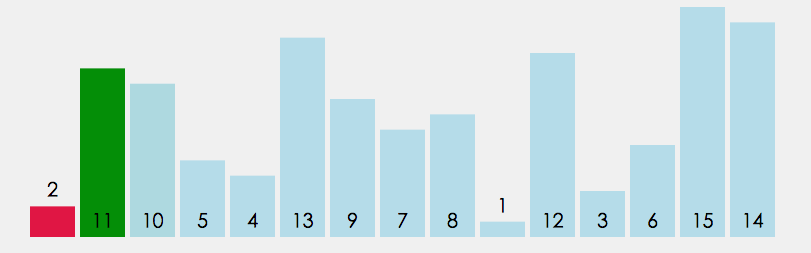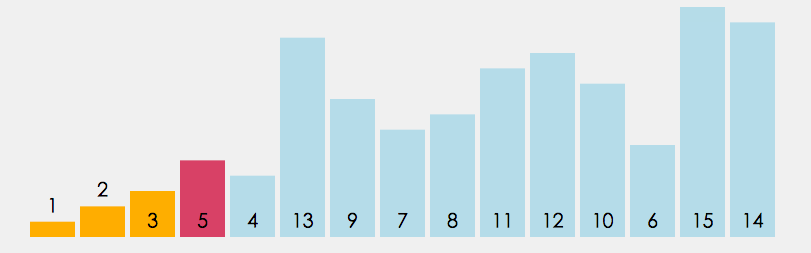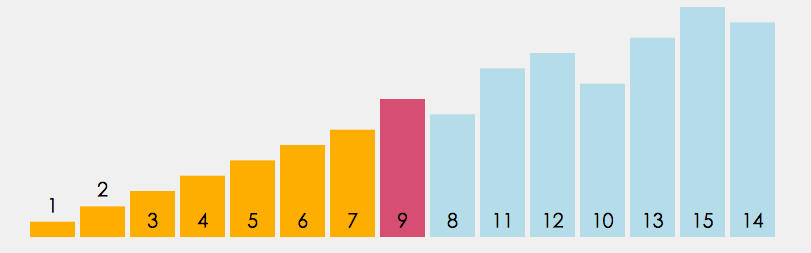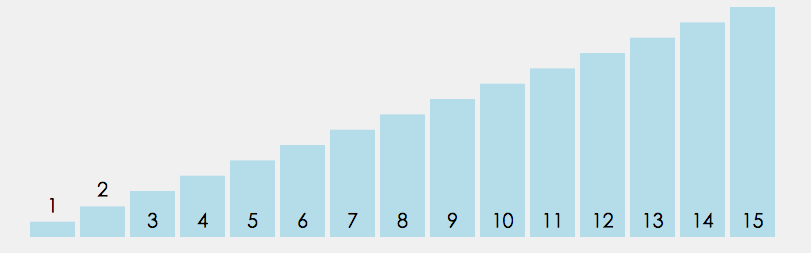
3.2 代碼:
void SelectSort(int* arr, int n)
{int begin = 0;int end = n - 1;while (begin < end){int mini = begin;int maxi = begin;for (int i = begin+1; i <= end; i++){if (arr[mini] > arr[i]){mini = i;}if (arr[maxi] < arr[i]){maxi = i;}}//mini begin//maxi end//避免maxi begini都在同一個位置,begin和mini交換之后,maxi數據變成了最小的數據if (maxi == begin){maxi = mini;}Swap(&arr[maxi], &arr[end]);Swap(&arr[mini], &arr[begin]);--end;++begin;}
}1.每次在剩余序列中找最大的和最小的,最大的交換至后面,最小的交換至前面
2.
進入循環,mini找到1,maxi還是在9,此時我們將再將mini和begin交換,maxi與end交換,
end++,begin–跳出循環,排序完成仍然是931,出現了問題。所以需要
if (maxi == begin){maxi = mini;}這樣當我們將mini和begin交換完成后,maxi所指向的仍然是最大的數據,將其再與end交換
3.3 復雜度:
1.時間復雜度:O(N^2)
2.空間復雜度:O(1)
四 堆排序:
堆排序是指利?堆積樹(堆)這種數據結構所設計的?種排序算法,它是選擇排序的? 種。它是通過堆來進?選擇數據。需要注意的是排升序要建?堆,排降序建?堆。
在 【數據結構篇】順序結構二叉樹(堆)的堆排序已經講過了此方法,這里就不贅述了。
以上就是【數據結構篇】排序1(插入排序與選擇排序)的全部內容,歡迎指正~?🌹🌹🌹
碼文不易,還請多多關注支持,這是我持續創作的最大動力!




)



)
——最小生成樹)










