目錄
7.1 整體結構
7.2 卷積層
7.2.1 全連接層存在的問題
7.2.2 卷積運算
7.2.3 填充
7.2.5 3維數據的卷積運算
7.2.6 結合方塊思考
7.2.7 批處理
7.3 池化層
7.4 卷積層和池化層的實現
7.4.1 4維數組
7.4.2 基于 im2col的展開
7.4.3 卷積層的實現
7.4.4 池化層的實現
7.5 CNN的實現
7.6 CNN的可視化
7.6.1 第 1層權重的可視化
7.6.2 基于分層結構的信息提取
7.7 具有代表性的 CNN
7.7.1 LeNet
7.7.2 AlexNet
7.8 小結
CNN被用于圖像識別、語音識別等各種場合,在圖像識別的比賽中,基于深度學習的方法幾乎都以CNN為基礎。本章將詳細介紹CNN的結構,并用Python實現其處理內容。
7.1 整體結構
CNN和之前介紹的神經網絡一樣,可以像樂高積木一樣通過組裝層來構建。不過,CNN中新出現了卷積層(Convolution層)和池化層(Pooling層).
之前介紹的神經網絡中,相鄰層的所有神經元之間都有連接,這稱為全連接(fully-connected)。另外,我們用Affine層實現了全連接層。如果使用這個Affine層,一個5層的全連接的神經網絡就可以通過圖7-1所示的網絡結構來實現。
如圖7-1所示,全連接的神經網絡中,Affine層后面跟著激活函數ReLU層(或者Sigmoid層)。這里堆疊了4層“Affine-ReLU”組合,然后第5層是Affine層,最后由Softmax層輸出最終結果(概率)。
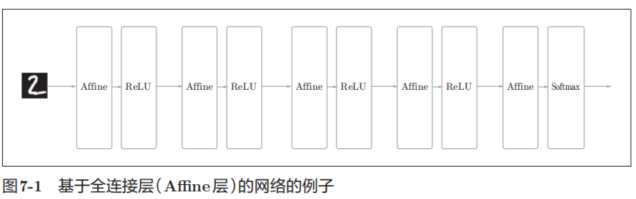
圖7-2是CNN的一個例子。
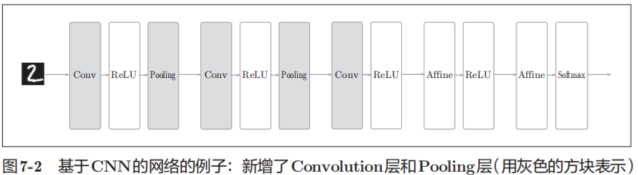
CNN 的層的連接順序是“Convolution - ReLU -(Pooling)”(Pooling層有時會被省略)。這可以理解為之前的“Affine - ReLU”連接被替換成了“Convolution - ReLU -(Pooling)”連接。
還需要注意的是,在圖7-2的CNN中,靠近輸出的層中使用了之前的“Affi ne - ReLU”組合。此外,最后的輸出層中使用了之前的“Affine -Softmax”組合。這些都是一般的CNN中比較常見的結構。
7.2 卷積層
CNN中出現了一些特有的術語,比如填充、步幅等。此外,各層中傳遞的數據是有形狀的數據(比如,3維數據),這與之前的全連接網絡不同,因此剛開始學習CNN時可能會感到難以理解。
7.2.1 全連接層存在的問題
全連接層存在什么問題呢?那就是數據的形狀被“忽視”了。比如,輸入數據是圖像時,圖像通常是高、長、通道方向上的3維形狀。但是,向全連接層輸入時,需要將3維數據拉平為1維數據。實際上,前面提到的使用了MNIST數據集的例子中,輸入圖像就是1通道、高28像素、長28像素的(1, 28, 28)形狀,但卻被排成1列,以784個數據的形式輸入到最開始的Affine層。
圖像是3維形狀,這個形狀中應該含有重要的空間信息。比如,空間上鄰近的像素為相似的值、RBG的各個通道之間分別有密切的關聯性、相距較遠的像素之間沒有什么關聯等,3維形狀中可能隱藏有值得提取的本質模式。但是,因為全連接層會忽視形狀,將全部的輸入數據作為相同的神經元(同一維度的神經元)處理,所以無法利用與形狀相關的信息。
而卷積層可以保持形狀不變。當輸入數據是圖像時,卷積層會以3維數據的形式接收輸入數據,并同樣以3維數據的形式輸出至下一層。因此,在CNN中,可以(有可能)正確理解圖像等具有形狀的數據。
另外,CNN 中,有時將卷積層的輸入輸出數據稱為特征圖(feature map)。其中,卷積層的輸入數據稱為輸入特征圖(input feature map),輸出數據稱為輸出特征圖(output feature map)。本書中將“輸入輸出數據”和“特征圖”作為含義相同的詞使用。
7.2.2 卷積運算
卷積層進行的處理就是卷積運算。卷積運算相當于圖像處理中的“濾波器運算”。
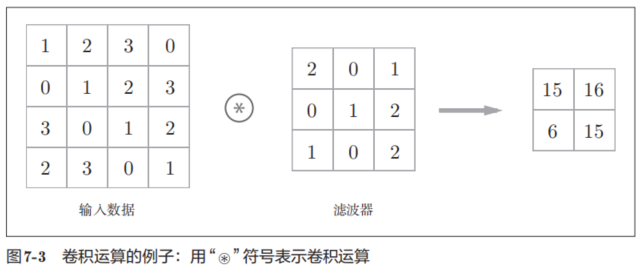
在這個例子中,輸入數據是有高長方向的形狀的數據,濾波器也一樣,有高長方向上的維度。
現在來解釋一下圖7-3的卷積運算的例子中都進行了什么樣的計算。圖7-4中展示了卷積運算的計算順序。
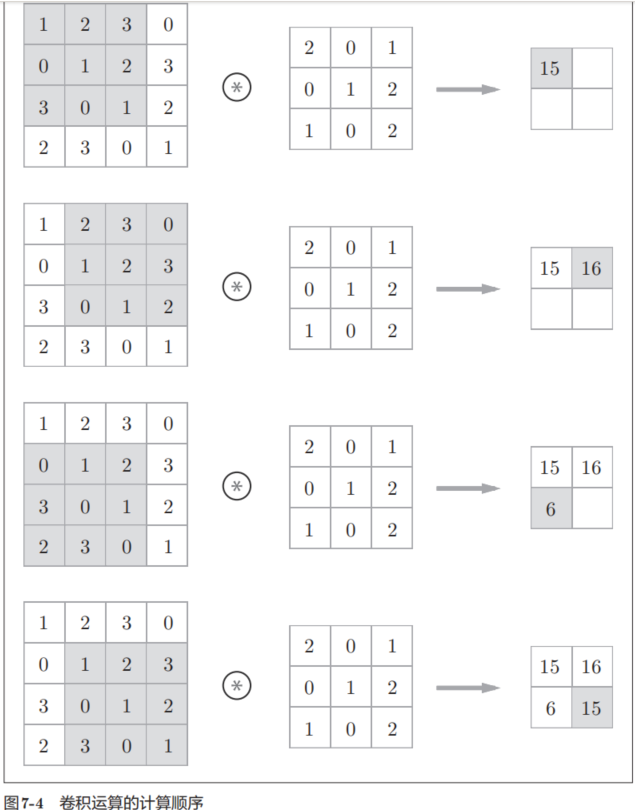
如圖7-4所示,將各個位置上濾波器的元素和輸入的對應元素相乘,然后再求和(有時將這個計算稱為乘積累加運算)。然后,將這個結果保存到輸出的對應位置。將這個過程在所有位置都進行一遍,就可以得到卷積運算的輸出。
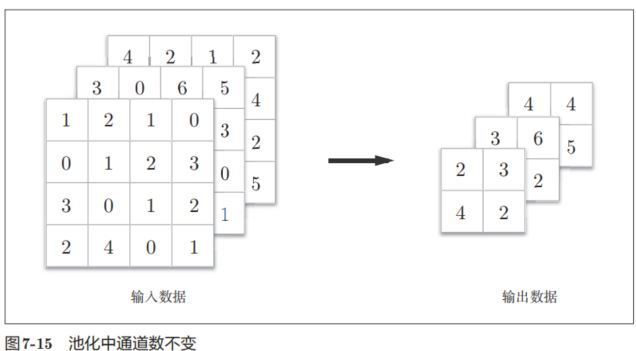
在全連接的神經網絡中,除了權重參數,還存在偏置。CNN中,濾波器的參數就對應之前的權重。并且,CNN中也存在偏置。圖7-3的卷積運算的例子一直展示到了應用濾波器的階段。包含偏置的卷積運算的處理流如圖7-5所示。
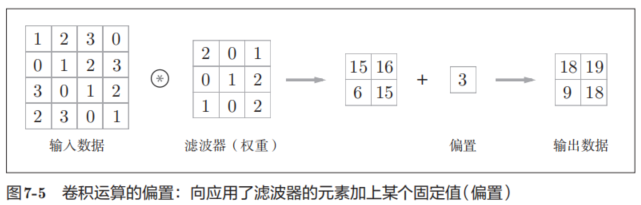
7.2.3 填充
在進行卷積層的處理之前,有時要向輸入數據的周圍填入固定的數據(比如0等),這稱為填充(padding),是卷積運算中經常會用到的處理。比如,在圖7-6的例子中,對大小為(4, 4)的輸入數據應用了幅度為1的填充。“幅度為1的填充”是指用幅度為1像素的0填充周圍。
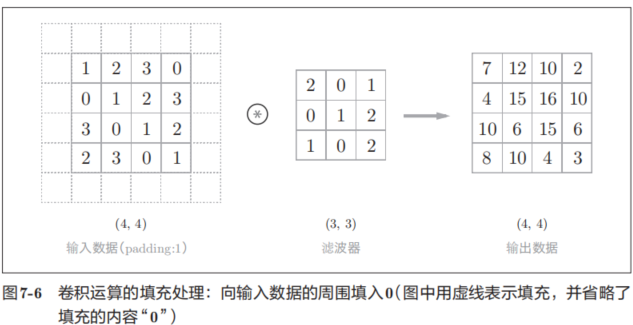
如圖7-6所示,通過填充,大小為(4, 4)的輸入數據變成了(6, 6)的形狀。然后,應用大小為(3, 3)的濾波器,生成了大小為(4, 4)的輸出數據。這個例子中將填充設成了1,不過填充的值也可以設置成2、3等任意的整數。在圖7-5的例子中,如果將填充設為2,則輸入數據的大小變為(8, 8);如果將填充設為3,則大小變為(10, 10)。
使用填充主要是為了調整輸出的大小。比如,對大小為(4, 4)的輸入數據應用(3, 3)的濾波器時,輸出大小變為(2, 2),相當于輸出大小比輸入大小縮小了 2個元素。這在反復進行多次卷積運算的深度網絡中會成為問題。為什么呢?因為如果每次進行卷積運算都會縮小空間,那么在某個時刻輸出大小就有可能變為 1,導致無法再應用卷積運算。為了避免出現這樣的情況,就要使用填充。在剛才的例子中,將填充的幅度設為 1,那么相對于輸入大小(4, 4),輸出大小也保持為原來的(4, 4)。因此,卷積運算就可以在保持空間大小不變的情況下將數據傳給下一層。
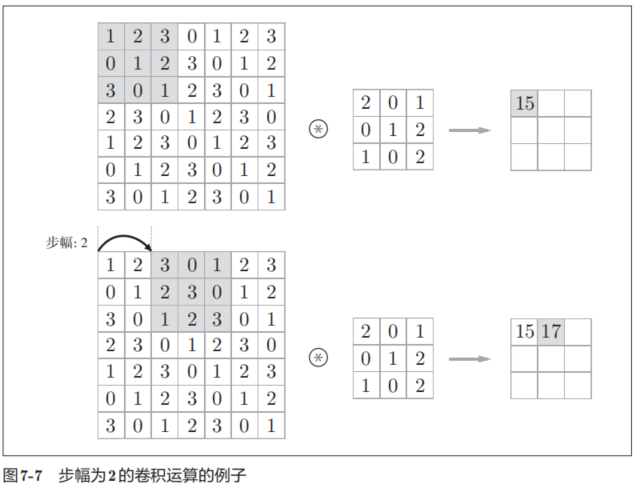
在圖7-7的例子中,對輸入大小為(7, 7)的數據,以步幅2應用了濾波器。通過將步幅設為2,輸出大小變為(3, 3)。像這樣,步幅可以指定應用濾波器的間隔。
綜上,增大步幅后,輸出大小會變小。而增大填充后,輸出大小會變大。如果將這樣的關系寫成算式,會如何呢?接下來,我們看一下對于填充和步幅,如何計算輸出大小。
這里,假設輸入大小為(H, W),濾波器大小為(FH, FW),輸出大小為(OH, OW),填充為P,步幅為S。此時,輸出大小可通過式(7.1)進行計算。
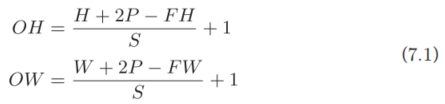
現在,我們使用這個算式,試著做幾個計算。

例3
輸入大小:(28, 31);填充:2;步幅:3;濾波器大小:(5, 5)
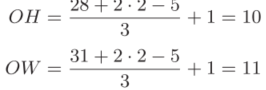
里需要注意的是,雖然只要代入值就可以計算輸出大小,但是所設定的值必須使式(7.1)中的
![]()
分別可以除盡。當輸出大小無法除盡時(結果是小數時),需要采取報錯等對策。
7.2.5 3維數據的卷積運算
之前的卷積運算的例子都是以有高、長方向的2維形狀為對象的。但是,圖像是3維數據,除了高、長方向之外,還需要處理通道方向。這里,我們按照與之前相同的順序,看一下對加上了通道方向的3維數據進行卷積運算的例子。
圖7-8是卷積運算的例子,圖7-9是計算順序。這里以3通道的數據為例,展示了卷積運算的結果。和2維數據時(圖7-3的例子)相比,可以發現縱深方向(通道方向)上特征圖增加了。通道方向上有多個特征圖時,會按通道進行輸入數據和濾波器的卷積運算,并將結果相加,從而得到輸出。
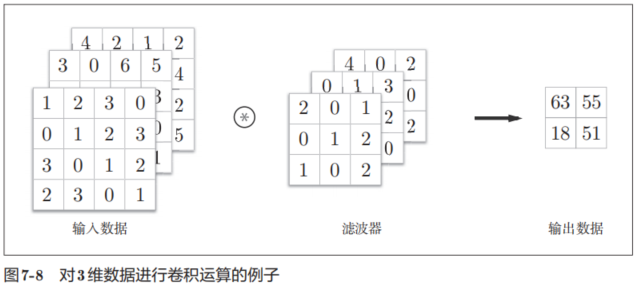
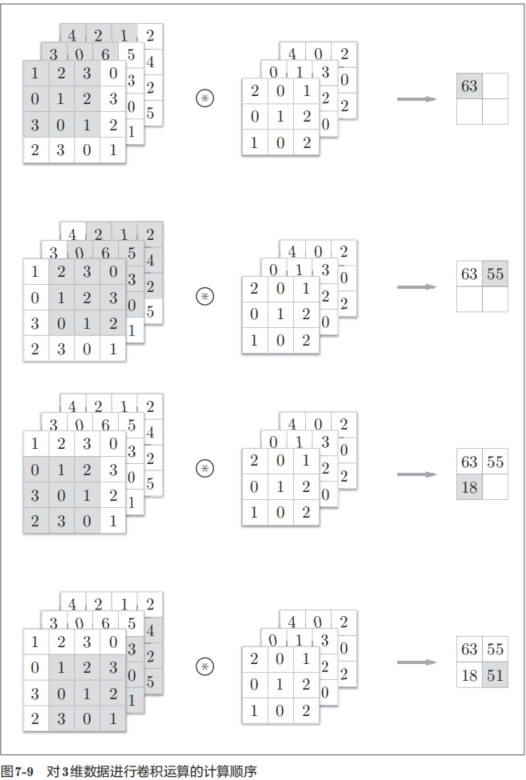
需要注意的是,在3維數據的卷積運算中,輸入數據和濾波器的通道數要設為相同的值。在這個例子中,輸入數據和濾波器的通道數一致,均為3。
7.2.6 結合方塊思考
將數據和濾波器結合長方體的方塊來考慮,3維數據的卷積運算會很容易理解。方塊是如圖7-10所示的3維長方體。把3維數據表示為多維數組時,書寫順序為(channel, height, width)。比如,通道數為C、高度為H、長度為W的數據的形狀可以寫成(C, H, W)。濾波器也一樣,要按(channel, height, width)的順序書寫。比如,通道數為C、濾波器高度為FH(Filter Height)、長度為FW(Filter Width)時,可以寫成(C, FH, FW)。
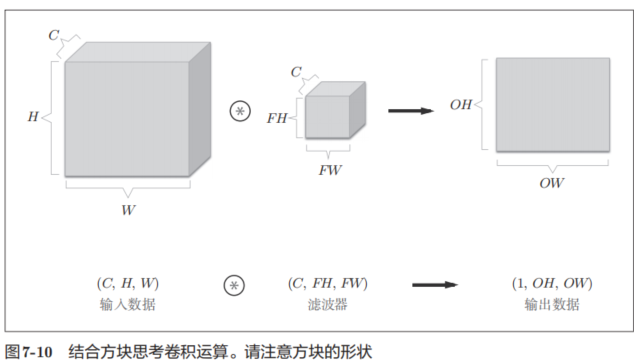
在這個例子中,數據輸出是1張特征圖。所謂1張特征圖,換句話說,就是通道數為1的特征圖。那么,如果要在通道方向上也擁有多個卷積運算的輸出,該怎么做呢?為此,就需要用到多個濾波器(權重)。用圖表示的話,如圖7-11所示。
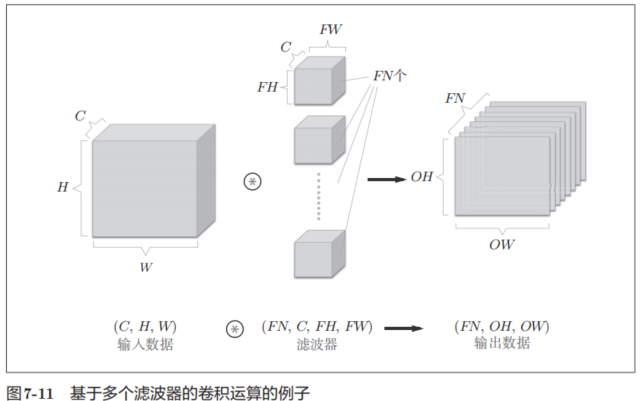
圖7-11中,通過應用FN個濾波器,輸出特征圖也生成了FN個。如果將這FN個特征圖匯集在一起,就得到了形狀為(FN, OH, OW)的方塊。將這個方塊傳給下一層,就是CNN的處理流。
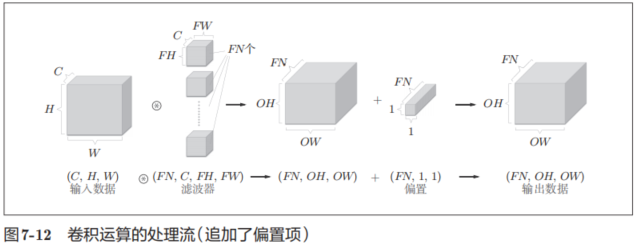
如果進一步追加偏置的加法運算處理,則結果如下面的圖7-12所示。
圖7-12中,每個通道只有一個偏置。這里,偏置的形狀是(FN, 1, 1),濾波器的輸出結果的形狀是(FN, OH, OW)。這兩個方塊相加時,要對濾波器的輸出結果(FN, OH, OW)按通道加上相同的偏置值。
7.2.7 批處理
我們希望卷積運算也同樣對應批處理。為此,需要將在各層間傳遞的數據保存為4維數據。具體地講,就是按(batch_num, channel, height, width)的順序保存數據。比如,將圖7-12中的處理改成對N個數據進行批處理時,數據的形狀如圖7-13所示。
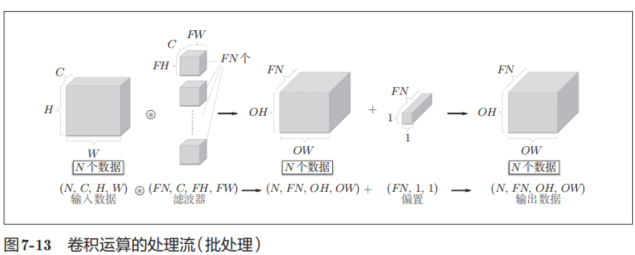
圖7-13的批處理版的數據流中,在各個數據的開頭添加了批用的維度。像這樣,數據作為4維的形狀在各層間傳遞。這里需要注意的是,網絡間傳遞的是4維數據,對這N個數據進行了卷積運算。也就是說,批處理將N次的處理匯總成了1次進行。
7.3 池化層
池化是縮小高、長方向上的空間的運算。比如,如圖7-14所示,進行將2 × 2的區域集約成1個元素的處理,縮小空間大小。
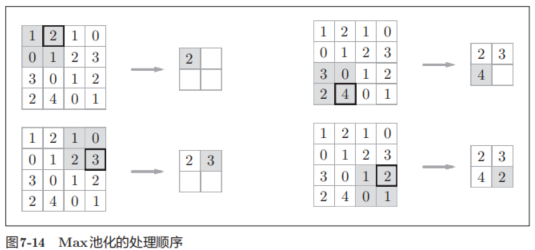
圖7-14的例子是按步幅2進行2 × 2的Max池化時的處理順序。“Max池化”是獲取最大值的運算,“2 × 2”表示目標區域的大小。如圖所示,從2 × 2的區域中取出最大的元素。此外,這個例子中將步幅設為了2,所以2 × 2的窗口的移動間隔為2個元素。另外,一般來說,池化的窗口大小會和步幅設定成相同的值。比如,3 × 3的窗口的步幅會設為3,4 × 4的窗口的步幅會設為4等。
池化層的特征

對微小的位置變化具有魯棒性(健壯)
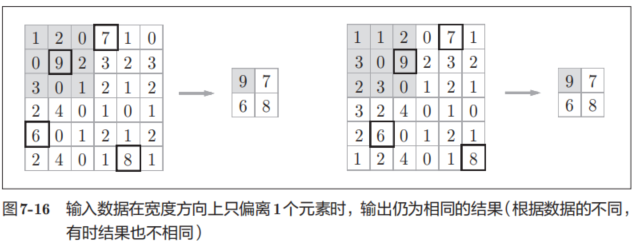
輸入數據發生微小偏差時,池化仍會返回相同的結果。因此,池化對輸入數據的微小偏差具有魯棒性。比如,3 × 3的池化的情況下,如圖7-16所示,池化會吸收輸入數據的偏差(根據數據的不同,結果有可能不一致)。
7.4 卷積層和池化層的實現
7.4.1 4維數組
如前所述,CNN中各層間傳遞的數據是4維數據。所謂4維數據,比如數據的形狀是(10, 1, 28, 28),則它對應10個高為28、長為28、通道為1的數據。用Python來實現的話,如下所示。

這里,如果要訪問第1個數據,只要寫x[0]就可以了(注意Python的索引是從0開始的)。同樣地,用x[1]可以訪問第2個數據。
![]()
如果要訪問第1個數據的第1個通道的空間數據,可以寫成下面這樣。
![]()
像這樣,CNN中處理的是4維數據,因此卷積運算的實現看上去會很復雜,但是通過使用下面要介紹的im2col這個技巧,問題就會變得很簡單。
7.4.2 基于 im2col的展開
如果老老實實地實現卷積運算,估計要重復好幾層的for語句。這樣的實現有點麻煩,而且,NumPy中存在使用for語句后處理變慢的缺點(NumPy中,訪問元素時最好不要用for語句)。這里,我們不使用for語句,而是使用im2col這個便利的函數進行簡單的實現。
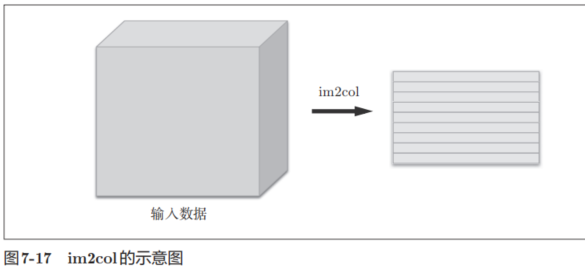
im2col是一個函數,將輸入數據展開以適合濾波器(權重)。如圖7-17所示,對3維的輸入數據應用im2col后,數據轉換為2維矩陣(正確地講,是把包含批數量的4維數據轉換成了2維數據)。
im2col會把輸入數據展開以適合濾波器(權重)。具體地說,如圖7-18所示,對于輸入數據,將應用濾波器的區域(3維方塊)橫向展開為1列。im2col會在所有應用濾波器的地方進行這個展開處理。
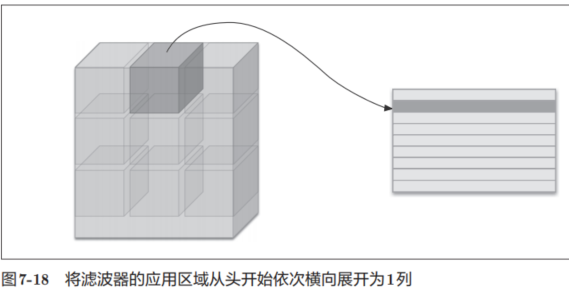
在圖7-18中,為了便于觀察,將步幅設置得很大,以使濾波器的應用區域不重疊。而在實際的卷積運算中,濾波器的應用區域幾乎都是重疊的。在濾波器的應用區域重疊的情況下,使用im2col展開后,展開后的元素個數會多于原方塊的元素個數。因此,通過歸結到矩陣計算上,可以有效地利用線性代數庫
im2col這個名稱是“image to column”的縮寫,翻譯過來就是“從圖像到矩陣”的意思。Caffe、Chainer 等深度學習框架中有名為im2col的函數,并且在卷積層的實現中,都使用了im2col。
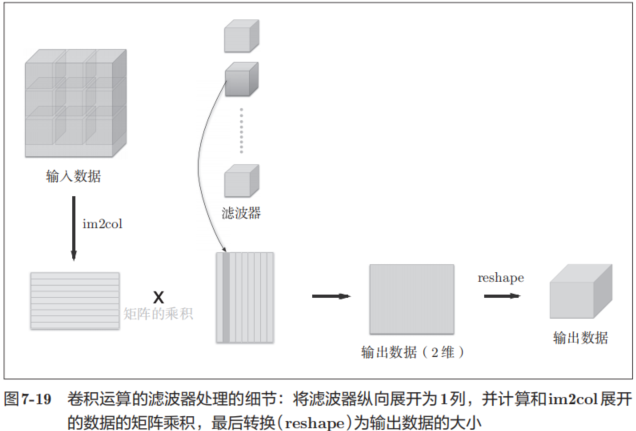
使用im2col展開輸入數據后,之后就只需將卷積層的濾波器(權重)縱向展開為1列,并計算2個矩陣的乘積即可(參照圖7-19)。這和全連接層的Affine層進行的處理基本相同。
如圖7-19所示,基于im2col方式的輸出結果是2維矩陣。因為CNN中數據會保存為4維數組,所以要將2維輸出數據轉換為合適的形狀。以上就是卷積層的實現流程。
7.4.3 卷積層的實現
class Convolution:def __init__(self, W, b, stride=1, pad=0):self.W = W # 卷積濾波器權重,形狀為 (FN, C, FH, FW)# FN:濾波器個數, C:通道數, FH:濾波器高, FW:濾波器寬self.b = b # 偏置參數self.stride = stride # 卷積步長self.pad = pad # 填充大小def forward(self, x):FN, C, FH, FW = self.W.shape # 獲取卷積核的維度:濾波器數量,通道數,高度,寬度N, C, H, W = x.shape # 獲取輸入數據的維度:批大小,通道數,高度,寬度# 計算輸出特征圖的尺寸out_h = int(1 + (H + 2*self.pad - FH) / self.stride) # 輸出高度out_w = int(1 + (W + 2*self.pad - FW) / self.stride) # 輸出寬度col = im2col(x, FH, FW, self.stride, self.pad) # 將輸入圖像轉換為列矩陣col_W = self.W.reshape(FN, -1).T # 將卷積核重塑并轉置為二維矩陣out = np.dot(col, col_W) + self.b # 矩陣乘法實現卷積計算并加上偏置# 將輸出結果重塑為標準四維格式:(批大小, 濾波器數量, 輸出高度, 輸出寬度)out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)return out卷積層的初始化方法將濾波器(權重)、偏置、步幅、填充作為參數接收。濾波器是 (FN, C, FH, FW)的 4 維形狀。另外,FN、C、FH、FW分別是 FilterNumber(濾波器數量)、Channel、Filter Height、Filter Width的縮寫。
展開濾波器的部分(代碼段中的粗體字)如圖7-19所示,將各個濾波器的方塊縱向展開為1列。這里通過reshape(FN,-1)將參數指定為-1,這是reshape的一個便利的功能。通過在reshape時指定為-1,reshape函數會自動計算-1維度上的元素個數,以使多維數組的元素個數前后一致。比如,(10, 3, 5, 5)形狀的數組的元素個數共有750個,指定reshape(10,-1)后,就會轉換成(10, 75)形狀的數組。
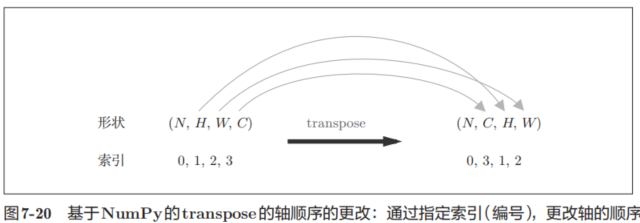
forward的實現中,最后會將輸出大小轉換為合適的形狀。轉換時使用了NumPy的transpose函數。transpose會更改多維數組的軸的順序。如圖7-20所示,通過指定從0開始的索引(編號)序列,就可以更改軸的順序。
以上就是卷積層的forward處理的實現。通過使用im2col進行展開,基本上可以像實現全連接層的Affine層一樣來實現(5.6節)。
接下來是卷積層的反向傳播的實現,因為和Affine層的實現有很多共通的地方,所以就不再介紹了。但有一點需要注意,在進行卷積層的反向傳播時,必須進行im2col的逆處理。除了使用col2im這一點,卷積層的反向傳播和Affine層的實現方式都一樣。
7.4.4 池化層的實現
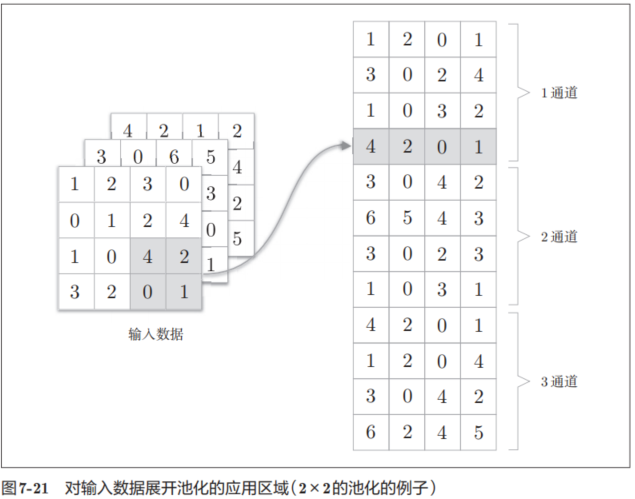
像這樣展開之后,只需對展開的矩陣求各行的最大值,并轉換為合適的形狀即可(圖7-22)。
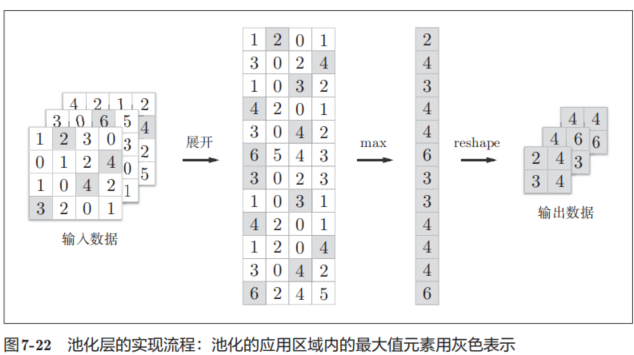
上面就是池化層的forward處理的實現流程。下面來看一下Python的實現示例。
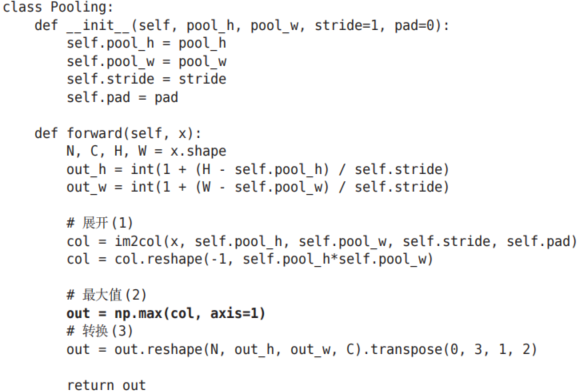
class Pooling:def __init__(self, pool_h, pool_w, stride=1, pad=0):self.pool_h = pool_h # 池化窗口的高度self.pool_w = pool_w # 池化窗口的寬度 self.stride = stride # 卷積步長(窗口移動的步長)self.pad = pad # 邊緣填充大小def forward(self, x):N, C, H, W = x.shape # 獲取輸入數據的維度:批大小,通道數,高度,寬度# 計算輸出特征圖的尺寸out_h = int(1 + (H - self.pool_h) / self.stride) # 輸出高度out_w = int(1 + (W - self.pool_w) / self.stride) # 輸出寬度# 展開(1):將輸入數據轉換為二維矩陣,每行代表一個池化窗口內的所有元素col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)# 調整矩陣形狀,將每個池化窗口展平為一行col = col.reshape(-1, self.pool_h * self.pool_w)# 最大值(2):對每一行(即每個池化窗口)取最大值,實現最大池化操作out = np.max(col, axis=1)# 轉換(3):將結果重塑為四維張量并調整維度順序為標準格式 (批大小, 通道數, 高, 寬)out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)return out # 返回池化后的輸出結果如圖7-22所示,池化層的實現按下面3個階段進行。
1.展開輸入數據。
2.求各行的最大值。
3.轉換為合適的輸出大小。
各階段的實現都很簡單,只有一兩行代碼。
以上就是池化層的forward處理的介紹。如上所述,通過將輸入數據展開為容易進行池化的形狀,后面的實現就會變得非常簡單。
7.5 CNN的實現
這里將由初始化參數傳入的卷積層的超參數從字典中取了出來(以方便后面使用),然后,計算卷積層的輸出大小。接下來是權重參數的初始化部分。

學習所需的參數是第1層的卷積層和剩余兩個全連接層的權重和偏置。 將這些參數保存在實例變量的params字典中。將第1層的卷積層的權重設為關鍵字W1,偏置設為關鍵字b1。同樣,分別用關鍵字W2、b2和關鍵字W3、b3來保存第2個和第3個全連接層的權重和偏置。
最后,生成必要的層。

從最前面開始按順序向有序字典(OrderedDict)的layers中添加層。只有最后的SoftmaxWithLoss層被添加到別的變量lastLayer中。
以上就是SimpleConvNet的初始化中進行的處理。像這樣初始化后,進行推理的predict方法和求損失函數值的loss方法就可以像下面這樣實現。

這里,參數x是輸入數據,t是教師標簽。用于推理的predict方法從頭開始依次調用已添加的層,并將結果傳遞給下一層。在求損失函數的loss方法中,除了使用 predict方法進行的 forward處理之外,還會繼續進行forward處理,直到到達最后的SoftmaxWithLoss層。
接下來是基于誤差反向傳播法求梯度的代碼實現。
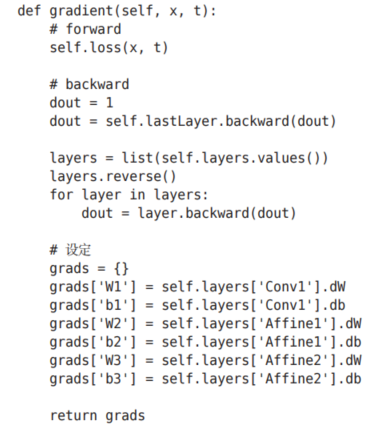
參數的梯度通過誤差反向傳播法(反向傳播)求出,通過把正向傳播和反向傳播組裝在一起來完成。因為已經在各層正確實現了正向傳播和反向傳播的功能,所以這里只需要以合適的順序調用即可。最后,把各個權重參數的梯度保存到grads字典中。這就是SimpleConvNet的實現。
7.6 CNN的可視化
CNN中用到的卷積層在“觀察”什么呢?本節將通過卷積層的可視化,探索CNN中到底進行了什么處理。
7.6.1 第 1層權重的可視化
剛才我們對MNIST數據集進行了簡單的CNN學習。當時,第1層的卷積層的權重的形狀是(30, 1, 5, 5),即30個大小為5 × 5、通道為1的濾波器。濾波器大小是5 × 5、通道數是1,意味著濾波器可以可視化為1通道的灰度圖像。現在,我們將卷積層(第1層)的濾波器顯示為圖像。這里,我們來比較一下學習前和學習后的權重,結果如圖7-24所示

圖7-24中,學習前的濾波器是隨機進行初始化的,所以在黑白的濃淡上沒有規律可循,但學習后的濾波器變成了有規律的圖像。我們發現,通過學習,濾波器被更新成了有規律的濾波器,比如從白到黑漸變的濾波器、含有塊狀區域(稱為blob)的濾波器等。
如果要問圖7-24中右邊的有規律的濾波器在“觀察”什么,答案就是它在觀察邊緣(顏色變化的分界線)和斑塊(局部的塊狀區域)等。比如,左半部分為白色、右半部分為黑色的濾波器的情況下,如圖7-25所示,會對垂直方向上的邊緣有響應。
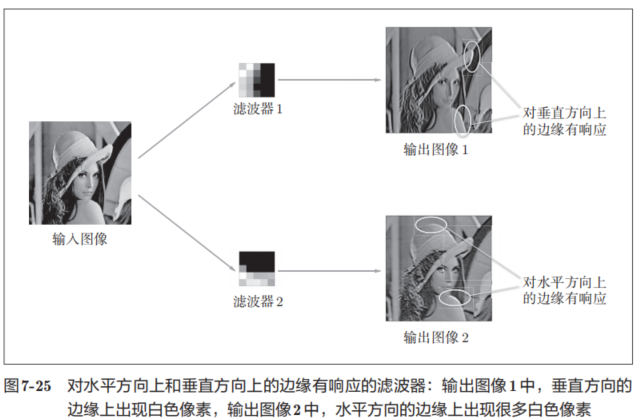
圖7-25中顯示了選擇兩個學習完的濾波器對輸入圖像進行卷積處理時的結果。我們發現“濾波器1”對垂直方向上的邊緣有響應,“濾波器2”對水平方向上的邊緣有響應。
由此可知,卷積層的濾波器會提取邊緣或斑塊等原始信息。而剛才實現的CNN會將這些原始信息傳遞給后面的層。
7.6.2 基于分層結構的信息提取
上面的結果是針對第1層的卷積層得出的。第1層的卷積層中提取了邊緣或斑塊等“低級”信息,那么在堆疊了多層的CNN中,各層中又會提取什么樣的信息呢?隨著層次加深,提取的信息(正確地講,是反映強烈的神經元)也越來越抽象。
圖7-26中展示了進行一般物體識別(車或狗等)的8層CNN。這個網絡結構的名稱是下一節要介紹的AlexNet。AlexNet網絡結構堆疊了多層卷積層和池化層,最后經過全連接層輸出結果。圖7-26的方塊表示的是中間數據,對于這些中間數據,會連續應用卷積運算
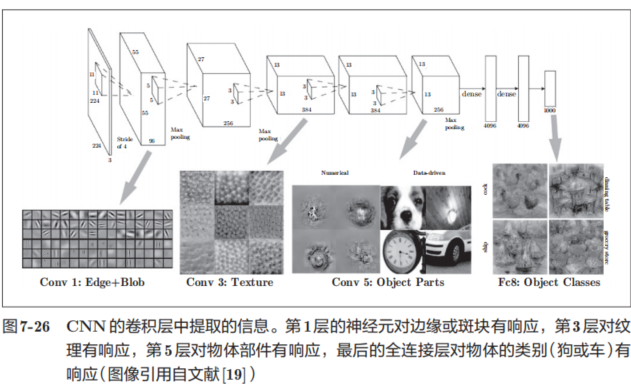
如圖7-26所示,如果堆疊了多層卷積層,則隨著層次加深,提取的信息也愈加復雜、抽象,這是深度學習中很有意思的一個地方。最開始的層對簡單的邊緣有響應,接下來的層對紋理有響應,再后面的層對更加復雜的物體部件有響應。也就是說,隨著層次加深,神經元從簡單的形狀向“高級”信息變化。
7.7 具有代表性的 CNN
關于CNN,迄今為止已經提出了各種網絡結構。這里,我們介紹其中特別重要的兩個網絡,一個是在1998年首次被提出的CNN元祖LeNet,另一個是在深度學習受到關注的2012年被提出的AlexNet
7.7.1 LeNet
LeNet在1998年被提出,是進行手寫數字識別的網絡。如圖7-27所示,它有連續的卷積層和池化層(正確地講,是只“抽選元素”的子采樣層),最后經全連接層輸出結果。
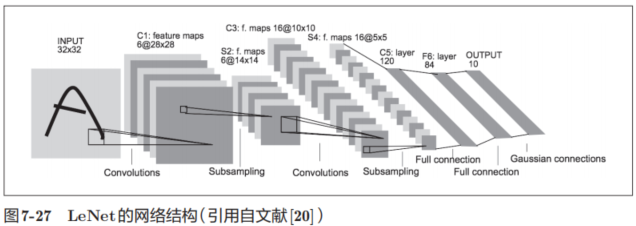
和“現在的CNN”相比,LeNet有幾個不同點。第一個不同點在于激活函數。LeNet中使用sigmoid函數,而現在的CNN中主要使用ReLU函數。此外,原始的LeNet中使用子采樣(subsampling)縮小中間數據的大小,而現在的CNN中Max池化是主流。
7.7.2 AlexNet
AlexNet是引發深度學習熱潮的導火線,不過它的網絡結構和LeNet基本上沒有什么不同,如圖7-28所示。
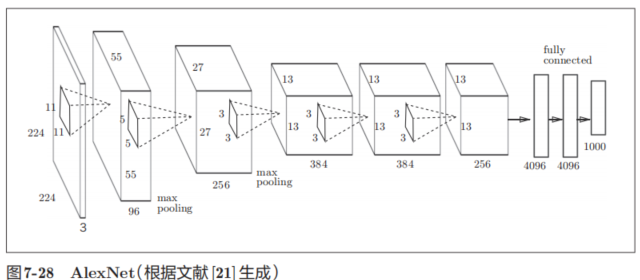
AlexNet疊有多個卷積層和池化層,最后經由全連接層輸出結果。雖然結構上AlexNet和LeNet沒有大的不同,但有以下幾點差異。

大多數情況下,深度學習(加深了層次的網絡)存在大量的參數。因此,學習需要大量的計算,并且需要使那些參數“滿意”的大量數據。可以說是 GPU和大數據給這些課題帶來了希望。
7.8 小結
? CNN在此前的全連接層的網絡中新增了卷積層和池化層。
? 使用im2col函數可以簡單、高效地實現卷積層和池化層。
? 通過CNN的可視化,可知隨著層次變深,提取的信息愈加高級。
? LeNet和AlexNet是CNN的代表性網絡。
? 在深度學習的發展中,大數據和GPU做出了很大的貢獻。


))
、GitHub Desktop(版本控制工具)、VSCode(代碼編輯器))

 sync.Pool)

 選擇器詳解:為什么它是“父選擇器”?如何實現真正的容器查詢?)

后訓練方法)





)
控制相機旋轉,限制角度)
歸并排序)

:項目探索)