線性函數與非線性函數是數學和工程領域中描述變量關系的基礎工具,二者在定義、性質、圖像特征及應用場景上存在本質差異。
以下從核心概念、數學特性、圖像對比、應用場景及實際案例五個維度展開詳細分析:
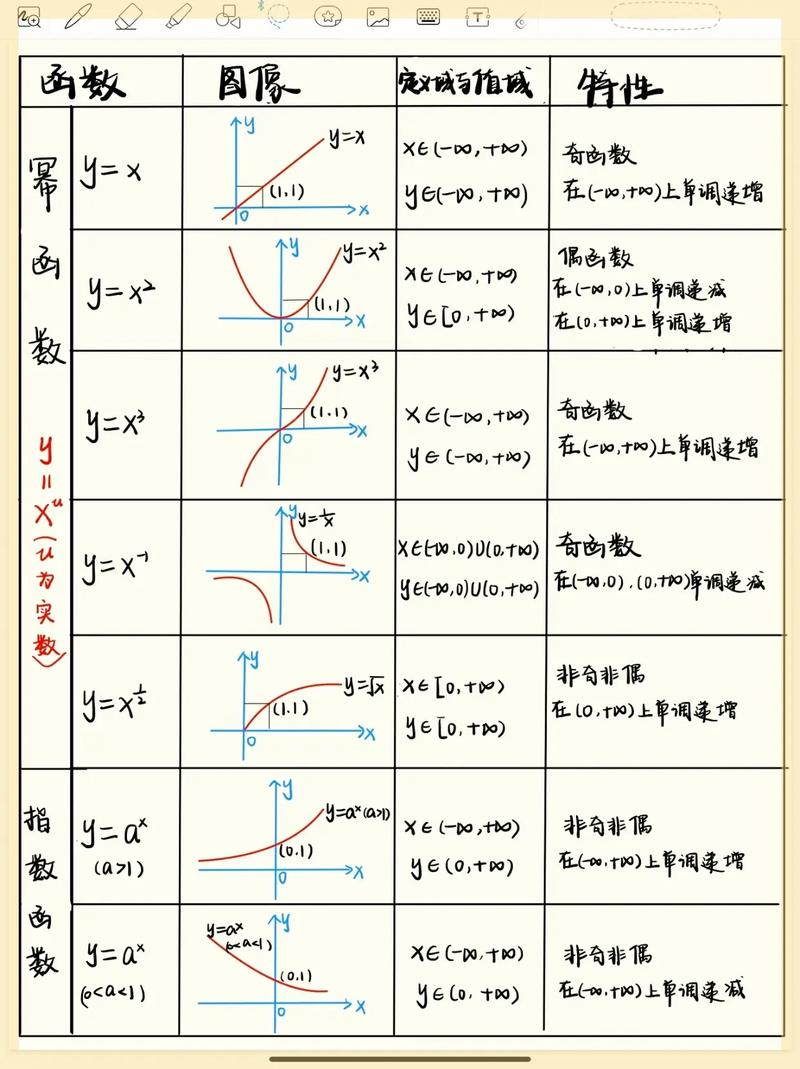
一、核心概念:線性 vs 非線性
- 線性函數
- 定義:在二維空間中,形如?y=kx+b(k=0)的函數稱為線性函數;在多維空間中,線性函數滿足疊加原理,即?f(ax+by)=af(x)+bf(y)。
- 本質:變量間的關系是比例且可疊加的,輸入與輸出呈均勻變化。因此,可以線性疊加。
- 示例:
- 一元線性函數:y=2x+3(斜率為2,截距為3)。
- 多元線性函數:z=3x+4y?5(兩個自變量x和y的線性組合)。
- 非線性函數
- 定義:不滿足疊加原理的函數,即?f(ax+by)=af(x)+bf(y)。
- 本質:變量間關系非比例且不可疊加,輸入變化與輸出變化之間不均勻。
- 示例:
- 二次函數:y=x2(拋物線)。
- 指數函數:y=ex(增長速率隨x增大而加快)。
- 對數函數:y=ln(x)(增長速率隨x增大而減緩)。
- 三角函數:y=sin(x)(周期性波動)。
二、數學特性對比
| 特性 | 線性函數 | 非線性函數 |
|---|---|---|
| 疊加原理 | 滿足?f(ax+by)=af(x)+bf(y) | 不滿足疊加原理 |
| 齊次性 | 滿足?f(kx)=kf(x) | 不滿足齊次性 |
| 可微性 | 連續可微,導數為常數(如?y=2x?的導數為2) | 可微但導數非恒定(如?y=x2?的導數為2x) |
| 積分性質 | 積分結果為多項式(如?∫ydx=21?x2+C) | 積分結果可能包含非多項式項(如?∫exdx=ex+C) |
| 解的存在性 | 線性方程組解唯一(或無解/無窮多解) | 非線性方程組可能有多解、無解或混沌解 |
三、圖像特征對比
- 線性函數圖像
- 形狀:直線(一元)或平面(多元)。
- 斜率:不同位置的變化率恒定,表示變化率固定(這是線性的關鍵)。
- 截距:與坐標軸的交點固定。
- 示例:y=?x+2?的圖像為斜率為-1、截距為2的直線。
- 非線性函數圖像
- 形狀:曲線、曲面或復雜幾何圖形。
- 斜率:不同位置的變化率不固定(如拋物線開口向上時斜率遞增)。
- 關鍵點:可能包含極值點(最大值/最小值)、拐點或漸近線。
- 示例:
- y=x2:開口向上的拋物線,頂點在原點。
- y=x1?:雙曲線,以x軸和y軸為漸近線。
四、應用場景對比
- 線性函數的應用:
- 經濟學:成本函數?C=500+10Q(固定成本500,單位變動成本10)。
- 物理學:勻速直線運動?s=vt(位移與時間成正比)。
- 工程學:電阻電路?V=IR(電壓與電流成正比)。
- 機器學習:線性回歸模型?y=β0?+β1?x(預測連續值)。
- 非線性函數的應用:
- 生物學:種群增長模型?dtdN?=rN(1?KN?)(Logistic增長,隨種群密度變化)。
- 金融學:復利計算?A=P(1+r)t(指數增長)。
- 控制理論:非線性控制系統(如機器人關節運動中的摩擦補償)。
- 深度學習:神經網絡激活函數(如ReLU?f(x)=max(0,x)、Sigmoid?f(x)=1+e?x1?)。
五、實際案例分析
- 案例1:線性回歸 vs 邏輯回歸
- 線性回歸:假設因變量?y?與自變量?x?呈線性關系?y=β0?+β1?x+?,用于預測連續值(如房價)。
- 邏輯回歸:通過Sigmoid函數將線性組合映射到概率空間?P(y=1∣x)=1+e?(β0?+β1?x)1?,用于分類問題(如垃圾郵件檢測)。
- 對比:邏輯回歸引入非線性變換(Sigmoid),將線性模型擴展至分類場景。
- 案例2:彈簧振子(線性) vs 杜芬振子(非線性)
- 線性彈簧振子:力與位移成正比?F=?kx,運動方程為?mdt2d2x?+kx=0,解為簡諧振動。
- 杜芬振子:引入立方項非線性力?F=?kx?αx3,運動方程為?mdt2d2x?+kx+αx3=0,解可能呈現混沌行為。
- 對比:非線性項導致系統行為復雜化,無法用簡單周期函數描述。
六、總結:線性與非線性的選擇依據
- 選擇線性函數:當變量關系簡單、可疊加,且需快速計算或解釋時(如經濟模型中的邊際成本分析)。
- 選擇非線性函數:當變量關系復雜、存在閾值效應、飽和現象或周期性波動時(如神經網絡中的特征提取、生物種群動態模擬)。
- 混合模型:實際系統中常結合線性與非線性部分(如控制理論中的PID控制器,比例項為線性,積分/微分項可能引入非線性效應)。

:原理講透 + 最小可運行 GPT)
)







![[CISCN2019 華北賽區 Day1 Web1]Dropbox](http://pic.xiahunao.cn/[CISCN2019 華北賽區 Day1 Web1]Dropbox)



:圖像輪廓)
函數參數類型問題解決)


)
