1.5、機器學習-回歸算法

1、線性回歸模型

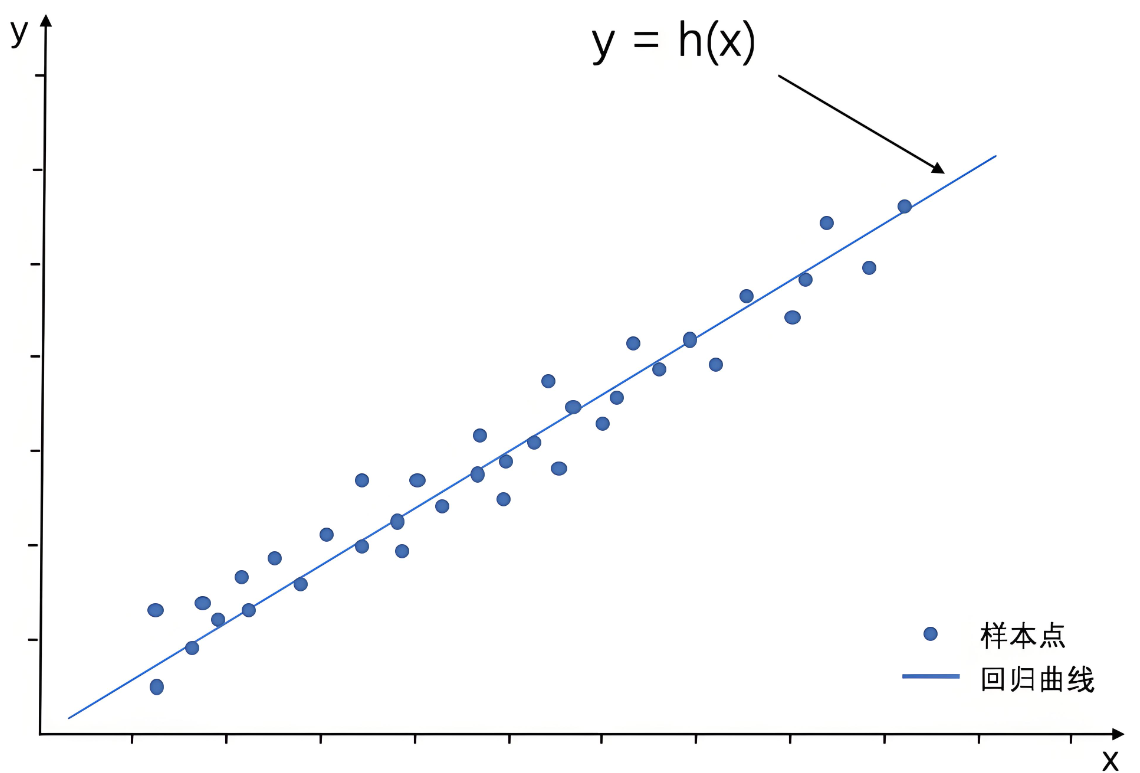
線性回歸模型(Liner Regression)，是利用線性擬合的方式來探尋數據背后的規律。通過搭建線性回歸模型，可以尋找這些散點（也稱樣本點）背后的趨勢線(也稱回歸曲線)。

借助回歸曲線，我們可以進行一些簡單的預測分析，或因果關系分析。

1.1、一元線性回歸數學原理

一元線性回歸模型也稱為簡單線性回歸模型，其形式可以通過如下方程公式表達：

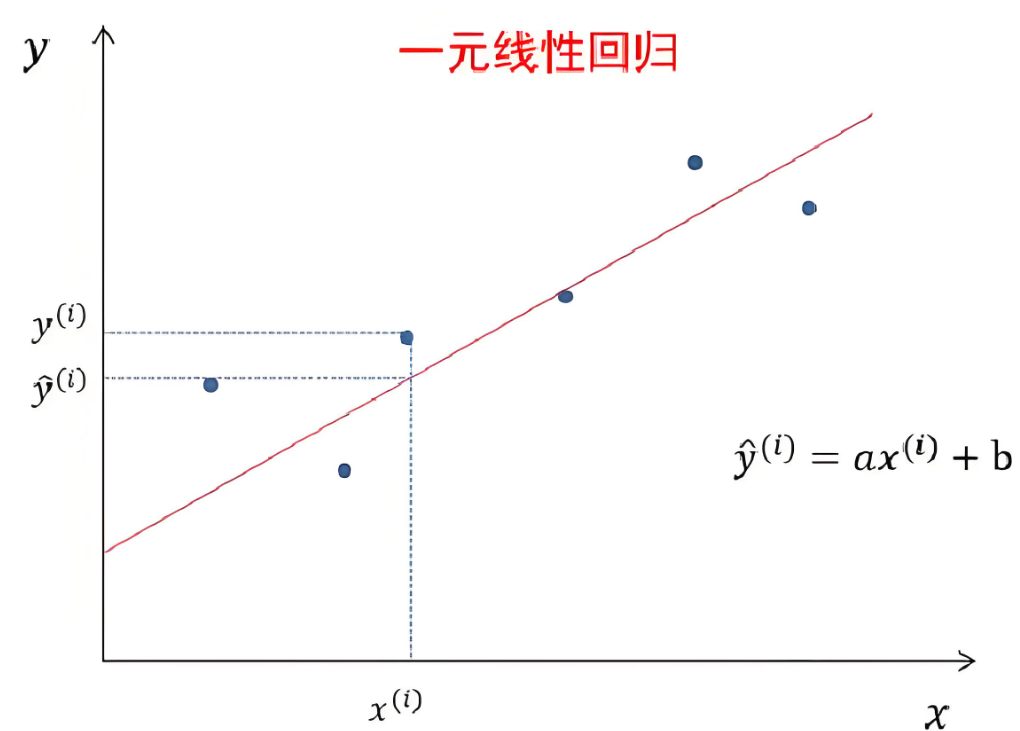
其中：y是目標(因)變量，x是特征(自)變量，a表示回歸系數，b表示截距。

一元線性回歸的目的，是擬合出一條線，使得預測值（）和實際值（）盡可能的接近，如果大部分點都落在擬合出來的線上，那么該線性回歸模型擬合效果較好。

此外，我們可以通過兩者差值平方和（，也稱為殘值平方和）來進行衡量，在機器學習領域，該殘差平方和也被稱之為回歸模型的損失函數。

1.2、一元線性回歸的代碼實現

在Python中，我們可以通過Scikit-learn工具庫，快速構建一元線性回歸模型。實現一元線性回歸的核心功能代碼如下：

from sklearn.linear_model import LinearRegression
from matplotlib import pyplot as plt
import matplotlib# pycharm工具:設置本地顯示后端
matplotlib.use('TkAgg')if __name__ == '__main__':X = [[1],[2],[3],[5]]Y = [2,4,6,8]# 1. 構建線性回歸模型對象lg = LinearRegression()# 2. 使用準備的自變量、因變量數據做訓練lg.fit(X, Y)# 3. 使用訓練好的模型預測新數據集y_pred = lg.predict([[4]])print(f"預測值:{y_pred[0]:.4f}") # 6.8571# 4. 繪制自變量、因變量組成的散點圖plt.scatter(X, Y, label='實際數據')# 5. 繪制訓練結果一元線性回歸方程plt.plot(X, lg.predict(X), color='red', label='回歸線')# 6. 展示執行效果|或使用Jupyter執行效果plt.show()

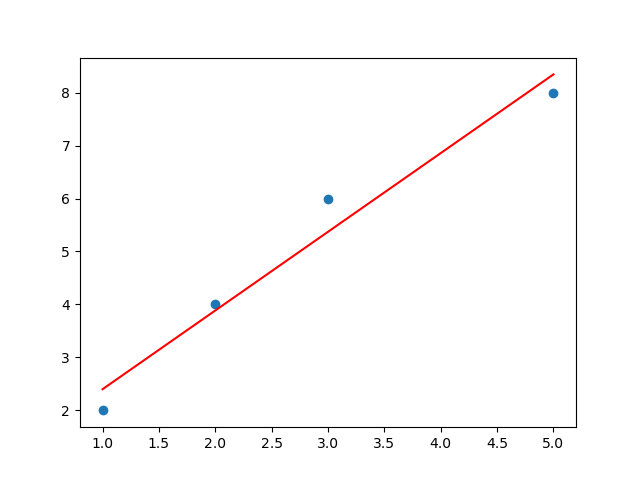
借助matplotlib工具，將模型進行可視化展示：

1.3、多元線性回歸

同理，多元線性回歸模型是在一元線性回歸模型基礎上，增加多個自變量，其形式可以通過如下方程公式表達：

其中：y是目標(因)變量，是特征(自)變量，表示權重系數，表示(誤差項)截距。

線性回歸使用均方誤差（MSE）作為損失函數：

1.3.1、經典案例

此處，我們使用波士頓房價數據集（Boston Housing Dataset）一個經典的回歸分析數據集，常用于預測房價。

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegressionif __name__ == '__main__':# 1. 數據加載data = pd.read_csv("boston_house_prices.csv", skiprows=1)# 2. 特征和標簽分離X = data.loc[:, :"LSTAT"].to_numpy()  # 特征y = data.loc[:, "MEDV"].to_numpy()    # 目標標簽# 3. 數據切分X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)# 4. 手動數據標準化(可用標準庫實現)mu = X_train.mean(axis=0)sigma = X_train.std(axis=0) + 1e-9X_train = (X_train - mu) / sigmaX_test = (X_test - mu) / sigma# 5. 模型訓練lr = LinearRegression()lr.fit(X=X_train, y=y_train)# 6. 預測與評估y_pred = lr.predict(X=X_test)mse = ((y_pred - y_test) ** 2).mean()print(f"均?誤差: {mse}")

1.3.2、實戰案例

案例：基于線性回歸模型的客戶價值預測

客戶價值可以幫助企業預測未來一段時間，客戶預計能夠為企業帶來多少利潤。嘗試結合已有的客戶價值數據表，完成以下功能。

1、結合客戶的價值數據，構建回歸模型；

歷史貸款金額	貸款次數	學歷	月收入	性別	是否有房產	客戶價值
50000	2	2	20000	1	1	2000
50000	3	1	15000	0	0	1200
100000	5	2	32000	1	0	1800
-	-	-	-	-	-	-

import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, classification_reportif __name__ == '__main__':# 1. 加載數據df = pd.read_csv("cust_value_data.csv", skiprows=1)# 2. 查看原始數據信息print("原始數據前10行:")print(df.head(10))print("\n數據信息:")print(df.info())print("缺失值統計:")print(df.isnull().sum())# 3. 找出存在null值的行null_rows = df[df.isnull().any(axis=1)]print("\n存在缺失值的行:")print(null_rows)# 4. 數據預處理# 4.1. 均值填充：將age為null的使用均值填充age_mean = df['age'].mean()df['age'].fillna(age_mean, inplace=True)# 4.2. 缺失值填充：將貸款均值填充history_debit_mean = df['history_debit'].mean()df['history_debit'].fillna(history_debit_mean, inplace=True)# 4.3. 缺失值填充：將月收入均值填充month_income_mean = df['month_income'].mean()df['month_income'].fillna(month_income_mean, inplace=True)# 5. 選擇特征和目標變量# 選擇特征列和目標列feature_cols = ['history_debit', 'debit_times', 'degree', 'month_income', 'sex', 'house_flag']X = df[feature_cols]y = df['customer_value']# 6. 數據切分（70%訓練，30%測試）X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# 7. 模型訓練model = LinearRegression()model.fit(X_train, y_train)# 8. 預測與評估y_pred = model.predict(X_test)# 5. 模型評估accuracy = accuracy_score(y_test, y_pred)report = classification_report(y_test, y_pred)print("模型準確率:", accuracy)print("分類報告:")print(report)

2、邏輯回歸模型

邏輯回歸（Logistic Regression）是線性回歸的一種擴展，主要用來處理分類模型，因其簡單有效、可解釋性強的特點，目前在多行業中被廣泛應用。

邏輯回歸的本質，是將線性回歸模型（-∞，+∞）通過Sigmoid()函數（也稱Logistic函數） $y = \frac{1} {1+e^{-z}}$ ?進行了非線性轉換，從而得到一個介于（0，1）之間的概率值，從而實現分類的效果。

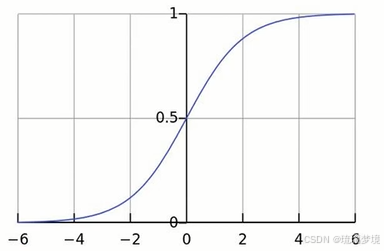
sigmoid函數代碼實現：

import numpy as np
import matplotlib.pyplot as pltdef sigmoid(x):"""Sigmoid 激活函數"""return 1 / (1 + np.exp(-x))if __name__ == '__main__':# 可視化 Sigmoid 函數x = np.linspace(-10, 10, 100)plt.plot(x, sigmoid(x))plt.grid()plt.title('Sigmoid Function')plt.xlabel('Input')plt.ylabel('Output')plt.show()

2.1、分類與回歸的區別

回歸模型：用于對連續變量進行預測，如預測收入范圍、房價變化、客戶價值等，線性回歸就是一種典型的回歸模型。

分類模型：用于對離散變量進行預測，分類模型預測的變量不是連續的，而是離散的一些類型。例如，使用常見的二分類模型，預測客戶是否違約、客戶是否會流失、腫瘤是良性還是惡性等。

2.2、經典案例

這是一個經典的二分類數據集，其目標是根據乳腺腫瘤的顯微圖像特征來診斷腫瘤是惡性（Malignant）還是良性（Benign)。

from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_splitif __name__ == '__main__':# 1. 加載數據X, y = load_breast_cancer(return_X_y=True)# 2. 數據切分X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)# 3. 數據標準化mu = X_train.mean(axis=0)sigma = X_train.std(axis=0) + 1e-9X_train = (X_train - mu) / sigmaX_test = (X_test - mu) / sigma# 4. 模型訓練lr = LogisticRegression()lr.fit(X=X_train, y=y_train)# 5. 預測與評估y_pred = lr.predict(X=X_test)accuracy = (y_pred == y_test).mean()print(f"準確率: {accuracy:.4f}")# 查看模型參數print(f"權重數量: {lr.coef_.shape}")print(f"偏置項: {lr.intercept_}")

2.3、實戰案例

案例：信用卡客戶流失預警模型

客戶流失預警模型可以用于預測客戶未來的流失情況。針對流失概率較大的客戶，可以采取適當的措施進行挽留，有效降低客戶的流失率。根據案例數據集，完成以下功能：

用戶ID	賬戶金額(元)	用戶年齡	學歷	性別	最后一次交易時間	上月交易傭金(元)	累計交易傭金(元)	使用信用卡年限(年	是否流失
10011	52000	32	本科	難	2025/6/2	232.21	3500	5	0

1、結合信用卡客戶流失數據，構建邏輯回歸模型（分類）

2、結合已有的數據判斷模型預測準確性，查看每名客戶的預估流失概率

import pandas as pd
from datetime import datetime
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, classification_reportif __name__ == '__main__':# 1. 加載數據df = pd.read_csv("credit_data.csv", skiprows=1)# 2. 查看原始數據信息print("原始數據前10行:")print(df.head(10))print("\n數據信息:")print(df.info())print("缺失值統計:")print(df.isnull().sum())# 3. 找出存在null值的行null_rows = df[df.isnull().any(axis=1)]print("\n存在缺失值的行:")print(null_rows)# 4. 數據預處理# 4.1. 刪除行：刪除amount為null的行df = df.dropna(subset=['amount'])# 4.2. 均值填充：將age為null的使用均值填充age_mean = df['age'].mean()df['age'].fillna(age_mean, inplace=True)# 4.3. 缺失值填充：將degree為null的使用"本科"填充df['degree'].fillna('本科', inplace=True)# 4.4. 刪除列：userId列(與訓練無關列),axis=1 表示刪除列df = df.drop('userId', axis=1)# 4.5.特征工程：性別編碼（男=0, 女=1）df['sex'] = df['sex'].map({'男': 0, '女': 1})current_date = datetime.now()# 4.6 最后一次交易時間處理為距現在時間的天數df['last_txn_time'] = pd.to_datetime(df['last_txn_time'])df['days_since_last_txn'] = (current_date - df['last_txn_time']).dt.days# 4.7 對學歷進行one-hot編碼，并避免多重共線性(刪除基準類別"本科")degree_dummies = pd.get_dummies(df['degree'], prefix='degree')if 'degree_本科' in degree_dummies.columns:degree_dummies = degree_dummies.drop('degree_本科', axis=1)# axis=1,指定df,degree_dummiesdf = pd.concat([df, degree_dummies], axis=1)# 5. 選擇特征和目標變量# 選擇特征列和目標列feature_cols = ['amount', 'age', 'last_month_kickback', 'accu_kickback', 'used_limit', 'days_since_last_txn', 'sex']X = df[feature_cols + degree_dummies.columns.tolist()]y = df['loss_flag']# 6. 數據切分（70%訓練，30%測試）X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# 7. 模型訓練model = LogisticRegression(random_state=42)model.fit(X_train, y_train)# 8. 預測與評估y_pred = model.predict(X_test)# 5. 模型評估accuracy = accuracy_score(y_test, y_pred)report = classification_report(y_test, y_pred)print("模型準確率:", accuracy)print("分類報告:")print(report)