6.1 Other dimensionality reduction methods
6.1 其他降維方法

前言

問題

降維與相關性的哲學問題
核心問題
為什么我們實際上能夠降維？
不同事物之間的相關性從何而來？

不僅僅是 PCA
不只是 PCA，還有其他機器學習方法也依賴相關性。
如果數據完全是隨機的、沒有結構，那么所有相關性都不存在，我們就無法降維。

舉例說明
即使兩個樣本在外觀或訓練測試上差異很大，看起來非常不同，但它們可能仍然遵循同樣的潛在規則。

結論
降維方法依賴于數據中的潛在相關性。
問題在于：這種潛在相關性到底從何而來？
類似的問題：為什么一個人的身高和體重之間會有關聯？

答案

數據中存在結構
在所謂“流形”的東西上，流形本身就是一種結構。
數據不是完全隨機的，而是有某種潛在結構。

PCA 的作用
PCA 能發現這種結構，盡管它假設的是線性關系，但現實中并不總是線性的。
因此，除了 PCA，我們還需要學習其他方法來處理這種“流形結構”。

核心問題
這些相關性（數據結構、流形）從何而來？
為什么我們能通過數據去推斷出維度？

答案
因為背后有物理約束。
數據的產生過程不是完全自由或隨機的，而是受到物理規律、自然法則的限制。如果數據真的完全是隨機的，就不會呈現出任何結構，也就談不上降維或發現相關性。

流形

數據所在的結構稱為流形。

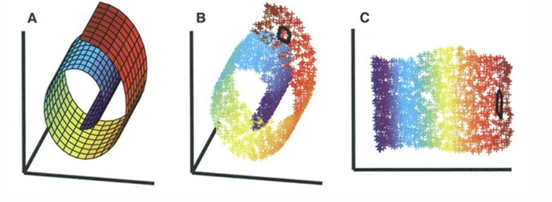
如果我們有兩個不同的變量，可以將其視為線性流形。但如果這個類型的數據結構或底層表面相當復雜。比如上圖經典的瑞士卷數據集，就是一個三維度數據和變量。
數據肯定有一個結構，數據所在的結構稱為它的流形。
我們感興趣的是有關物理數據約束信息的生成過程，希望幫助我們更好的進行預測任務。所以這個流形可能并不總是線性，因為我們有不同類型的維數或流形。

3 降維大綱

在真實數據集中，許多變量可能是相關的。因此，數據集的有效維度可能比特征數目更低。所以，數據實際上存在于某個 流形（manifold） 上。

降維方法

3.1 線性方法

PCA（主成分分析）
LDA（線性判別分析）
CCA ：Canonical Component Analysis 典型相關分析

3.2 非線性方法

3.2.1 流形學習方法（Manifold Learning）

目標：揭示隱藏在高維數據中的低維結構

Kernel PCA（核主成分分析）
MDS（多維尺度分析）
LLE（局部線性嵌入）
t-SNE

3.2.2 概率方法（Probabilistic Approaches）

ICA（獨立成分分析）

3.2.3 拓撲數據分析（Topological Data Analysis）

目標：保持數據的拓撲結構

方法：UMAP

3.3 監督降維方法

結合監督學習的降維技術

不相關與獨立

第二列相關性為0，但它們依然具有物理關系。

核化PCA（Kernelized PCA）

在下圖的情況中，在上面應用PCA，不會能找到最大方差的任何方向，因為所有方向都差不多。

如何找到流形在哪里？
通過觀察，我們知道，如果我們能夠找到一個圓形曲線而不是直線，將會是流形。
我們可以講數據投影到該圓弧上，實現縮小。

PCA 與核化PCA

區別在于把 協方差矩陣 $C$ 換成了核函數 $f(x)$。

PCA（主成分分析）
假設數據結構是 線性 的，通過協方差矩陣分解找到最大方差方向。
協方差矩陣：
$$C=\frac{1}{N}\sum _{i=1}^N(x_i?\bar{x})(x_i?\bar{x}{)}^T$$
優化目標：
$$\begin{gathered} \underset{w}{\max }{w}^{T}Cw \\ subject{w}^{T}w=1 \end{gathered}$$

核化PCA（Kernel PCA）
使用核函數將數據隱式映射到高維特征空間，在高維空間中做線性PCA，從而實現 非線性降維。

核矩陣：
$$K_{ij}=k(x_i,x_j)$$

優化目標：
$$\begin{gathered} \underset{\alpha }{\max }{\alpha }^{T}K\alpha \\ subject{\alpha }^T\alpha =1 \end{gathered}$$