1、題目描述

給定一個由?0?和?1?組成的矩陣?mat?，請輸出一個大小相同的矩陣，其中每一個格子是?mat?中對應位置元素到最近的?0?的距離。

兩個相鄰元素間的距離為?1?。

示例 1：

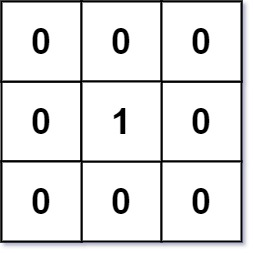
輸入：mat = [[0,0,0],[0,1,0],[0,0,0]]
輸出：[[0,0,0],[0,1,0],[0,0,0]]

示例 2：

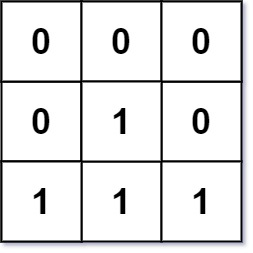
輸入：mat = [[0,0,0],[0,1,0],[1,1,1]]
輸出：[[0,0,0],[0,1,0],[1,2,1]]

提示：

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 104
• 1 <= m * n <= 104
• mat[i][j] is either 0 or 1.
• mat?中至少有一個?0?

---

2、代碼

#include <queue>    
#include <utility>  
#include <vector>   
using namespace std;class Solution
{public:// 計算矩陣中每個元素到最近0的距離vector<vector<int>> updateMatrix(vector<vector<int>>& mat){int row = mat.size();     int col = mat[0].size();  vector<vector<int>> ret(row, vector<int>(col, -1));// BFS隊列，用于存儲待處理的坐標（寬搜的核心數據結構）queue<pair<int, int>> q;// 第一步：初始化所有0的位置for (int i = 0; i < row; ++i) {for (int j = 0; j < col; ++j) {if (mat[i][j] == 0) {ret[i][j] = 0;   // 0到自身的距離為0q.push({i, j});  // 將所有0的坐標加入隊列，作為BFS的起點}}}// 定義四個方向的偏移量：上、下、左、右（用于遍歷相鄰單元格）vector<pair<int, int>> dirs = {{-1, 0},{1, 0},  {0, -1},{0, 1}};  // 第二步：多源BFS擴散計算距離while (!q.empty()) {// 取出隊列頭部的坐標（當前處理的單元格）auto [i, j] = q.front();// 遍歷四個相鄰方向for (auto [x, y] : dirs) {// 計算相鄰單元格的坐標int dx = i + x;  // 新行坐標 = 當前行 + 方向偏移int dy = j + y;  // 新列坐標 = 當前列 + 方向偏移// 檢查相鄰單元格是否有效：// 1. 不超出矩陣邊界（行和列都在有效范圍內）// 2. 該位置尚未計算距離（ret[dx][dy] == -1）if ((dx >= 0 && dx < row) && (dy >= 0 && dy < col) &&(ret[dx][dy] == -1)) {// 相鄰單元格的距離 = 當前單元格距離 + 1（因為相鄰）ret[dx][dy] = ret[i][j] + 1;// 將新計算的單元格加入隊列，用于后續擴散q.push({dx, dy});}}// 處理完當前單元格后出隊q.pop();}// 返回計算好的距離矩陣return ret;}
};

---

3、解題思路

1. 初始化部分：通過雙重循環找到所有 0 的位置，將其距離設為 0 并加入隊列，作為 BFS 的多源起點。
2. 方向數組：定義了上下左右四個方向的偏移量，避免了重復編寫判斷相鄰單元格的代碼。
3. BFS 核心邏輯：
   • 從隊列中取出當前單元格，遍歷其四個相鄰位置
   • 對每個有效且未計算距離的相鄰單元格，更新其距離（當前距離 + 1）并加入隊列
   • 保證每個單元格只被計算一次，且首次計算的距離就是到最近 0 的最短距離
4. 為什么有效：同時將所有 0 作為起點（距離為 0） 從 0 開始向外擴散，每個 1 被首次訪問時，一定是被最近的 0所擴散到的，因此首次計算的距離就是最短距離