【C語言16天強化訓練】從基礎入門到進階：Day 10

?🔥個人主頁：艾莉絲努力練劍

?專欄傳送門：《C語言》、《數據結構與算法》、C語言刷題12天IO強訓、LeetCode代碼強化刷題、洛谷刷題、C/C++基礎知識知識強化補充、C/C++干貨分享&學習過程記錄

🍉學習方向：C/C++方向學習者

??人生格言：為天地立心，為生民立命，為往圣繼絕學，為萬世開太平

前言：距離我們學完C語言已經過去一段時間了，在學習了初階的數據結構之后，博主還要更新的內容就是【C語言16天強化訓練】，之前博主更新過一個【C語言刷題12天IO強訓】的專欄，那個只是從入門到進階的IO模式真題的訓練。【C語言16天強化訓練】既有IO型，也有接口型。和前面一樣，今天依然是訓練五道選擇題和兩道編程算法題，希望大家能夠有所收獲！

一、五道選擇題

1.1? 題目1

1.2? 題目2

1.3? 題目3

1.4? 題目4

1.5? 題目5

二、兩道算法題

2.1??不用加減乘除做加法

2.1.1 題目理解

2.1.2 思路

2.2? 找到所有數組中消失的數字

2.2.1 題目理解

2.2.2 思路

2.2.3? 為什么選擇負號標記法？

2.2.4? 負號標記法的巧妙之處

2.2.5? 與其他方法的對比

結尾

一、五道選擇題

1.1? 題目1

題干：求函數返回值，傳入 -1 ，則在64位機器上函數返回（）

int func(int x)
{int count = 0;while (x){count++;x = x&(x - 1);//與運算} return count;
}

A. 死循環? ? ?B. 64? ? ?C. 32? ? ?D. 16

解析：正確答案就是B選項。

函數?func?的作用是計算整數?x?的二進制表示中1的個數（即漢明重量）。通過循環?x = x & (x - 1)?每次會消除二進制表示中最右邊的1，直到?x?變為0。

傳入?-1：在64位機器上，-1?的二進制表示是所有位都是1（即64個1）。因此，循環會執行64次（每次消除一個1），最后返回?count = 64。

1.2? 題目2

題干：讀代碼選結果（）

int count = 0;
int x = -1;
while(x)
{count++;x = x >> 1;
}
printf("%d",count)

A. 1? ? ?B. 2? ? ?C. 32? ? ?D. 死循環，沒結果

解析：正確答案就是D選項。

這里?x?是帶符號整數（默認是 signed int），初始為?-1（二進制所有位為1）。執行右移操作?x = x >> 1?是算術右移（對于負數，高位補1）。因此，無論右移多少次，x?始終不會變為0（因為高位一直補1，保持所有位為1，即始終為-1）。所以循環條件?x?永遠為非0，導致死循環。

1.3? 題目3

題干：下述賦值語句錯誤的是（）

A. a = (b = (c = 2 , d = 3))? ? ?B. i++? ? ?C. a / b = 2? ? ?D. a = a < a + 1

解析：正確答案就是C選項。

A.?正確，逗號表達式返回最后一個值（d=3），然后賦值給b，再賦值給a；
B.?正確，自增操作；
C. 錯誤，a/b是一個表達式（值），不能作為左值被賦值；
D.?正確，先計算a < a+1（恒為真，即1），然后賦值給a。

1.4? 題目4

題干：若有 int w=1, x=2, y=3, z=4; 則條件表達 w < x ? w : y < z ? y : z 的值是（）

A. 1? ? ? B. 2? ? ? C. 3? ? ? D. 4

解析：正確答案就是A選項。

題干所給表達式：w < x ? w : y < z ? y : z
結合性：從右到左（條件運算符是右結合），所以等價于：w < x ? w : (y < z ? y : z)

計算：w=1, x=2 -> w<x 為真（1），所以返回 w（即1）
因此w < x ? w : y < z ? y : z的值為1。

1.5? 題目5

題干：以下程序運行后的輸出結果是（）

int main()
{int a=1,b=2,m=0,n=0,k;k=(n=b<a)&&(m=a);printf("%d,%d\n",k,m);return 0;
}

A.?0,0? ? ?B. 0,1? ? ?C. 1,0? ? ?D. 1,1

解析：正確答案就是A選項。

（1）先計算 n = b<a（即n=2<1，為假，所以n=0）；

（2）由于 && 短路：第一個操作數 (n=b<a) 結果為0（假），所以第二個表達式 (m=a) 不會執行（m保持原值0）；

（3）k 為整個邏輯與的結果（0）。

因此輸出：k=0, m=0。

選擇題答案如下：

1.1? B

1.2? D

1.3? C

1.4? A

1.5? A

校對一下，大家都做對了嗎？

二、兩道算法題

2.1??不用加減乘除做加法

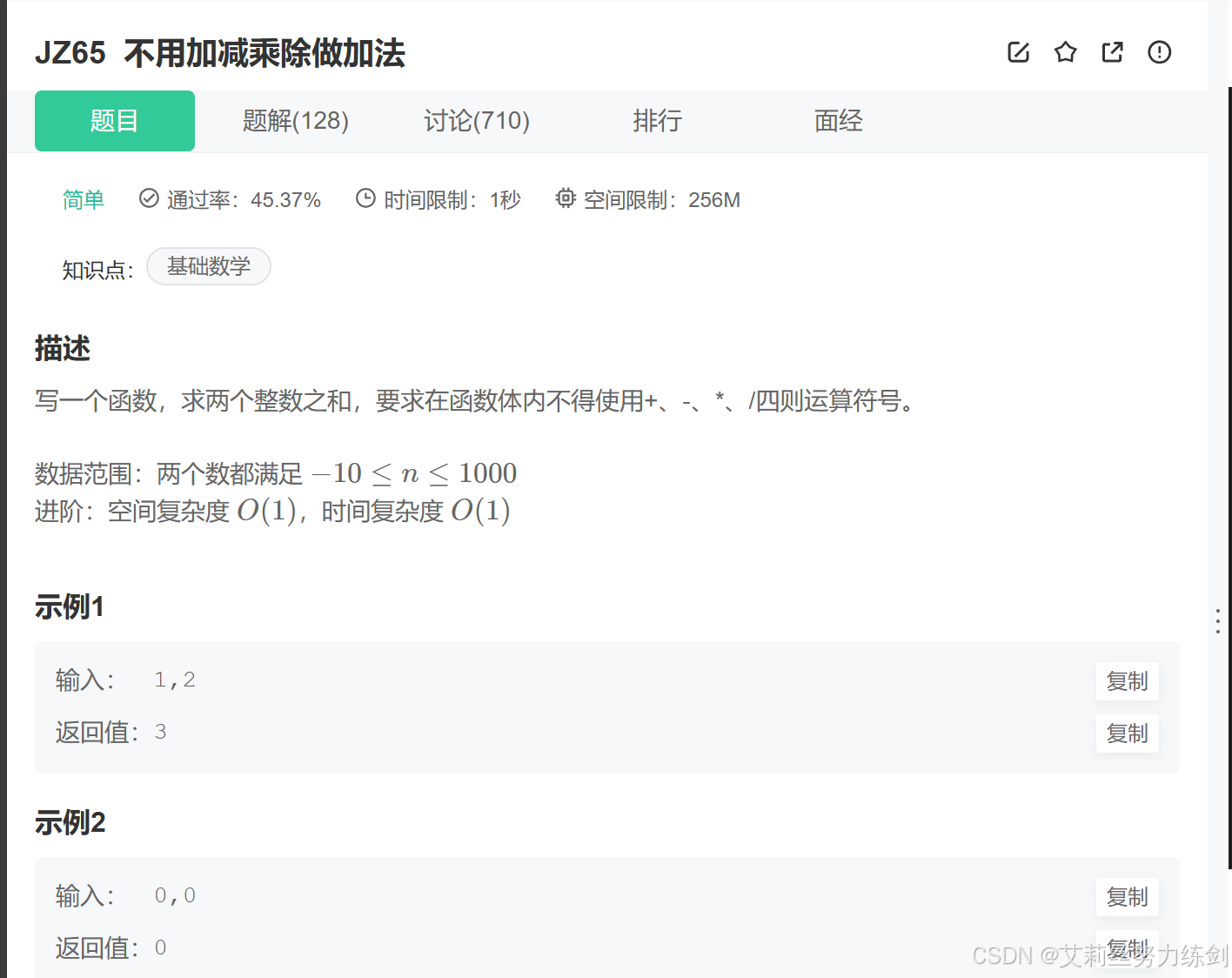
牛客鏈接：JZ65 不用加減乘除做加法

題目描述：

2.1.1 題目理解

為了解決這個問題，我們需要在不使用加減乘除運算符的情況下實現兩個整數的加法。我們可以利用位運算來模擬加法過程。

這道題是接口型的，下面是C語言的模版（如果是IO型就可以不用管它們了）——

2.1.2 思路

C語言思路：

1、算法原理：使用位運算模擬二進制加法。

（1）異或運算（~）：得到不考慮進位的和；

（2）與運算 + 左移（& + << 1）：得到進位值。

2、迭代過程：

（1）每次循環計算當前位的和（不考慮進位）和進位值；

（2）將和賦值給?num1，進位賦值給?num2；

（3）重復直到進位為0。

3、處理負數：由于C語言中使用補碼表示負數，該算法同樣適用于負數加法。

4、時間復雜度：O(1)，因為整數位數固定（通常是32位），最多循環32次。

代碼演示：

//C語言實現
/*** 代碼中的類名、方法名、參數名已經指定，請勿修改，直接返回方法規定的值即可*** @param num1 int整型* @param num2 int整型* @return int整型*/
int Add(int num1, int num2) 
{while (num2 != 0){int sum = num1 ^ num2;int carry = (num1 & num2) << 1;num1 = sum;num2 = carry;}return num1;
}

時間復雜度：O(1)；

空間復雜度：O(1)。

博主這里再展示一下完整的C語言代碼，包含了測試用例——

代碼演示：

//完整C語言代碼
#include <stdio.h>int Add(int num1, int num2) 
{while (num2 != 0) {int sum = num1 ^ num2;int carry = (num1 & num2) << 1;num1 = sum;num2 = carry;}return num1;
}int main() 
{// 測試用例printf("1 + 2 = %d\n", Add(1, 2));      // 輸出: 3printf("0 + 0 = %d\n", Add(0, 0));      // 輸出: 0printf("5 + 7 = %d\n", Add(5, 7));      // 輸出: 12printf("-1 + 1 = %d\n", Add(-1, 1));    // 輸出: 0printf("10 + -5 = %d\n", Add(10, -5));  // 輸出: 5return 0;
}

時間復雜度：O(1)；

空間復雜度：O(1)。

我們學習了C++之后也可以嘗試用C++來實現一下，看看自己前段時間C++學得怎么樣——

C++思路：

1、問題分析：題目要求不使用四則運算符號實現加法。我們可以使用位運算來模擬加法的過程。

2、關鍵觀察：二進制加法的每一位可以分解為：

（1）非進位和：使用異或運算（^）得到，即?num1 ^ num2；

（2）進位：使用與運算（&）并左移一位得到，即?(num1 & num2) << 1。

3、迭代過程：將非進位和與進位相加，直到進位為0。每次迭代都更新非進位和和進位，直到沒有進位為止。

代碼演示：

//C++實現
class Solution {
public:int Add(int num1, int num2){while (num2 != 0){int sum = num1 ^ num2;int carry = (num1 & num2) << 1;num1 = sum;num2 = carry;}return num1;}
};

時間復雜度：O(1)，空間復雜度：O(1)。

1、循環條件：當進位（num2）不為0時，繼續循環。

2、計算非進位和：使用異或運算?num1 ^ num2?得到當前位的和，不考慮進位。

3、計算進位：使用與運算?num1 & num2?并左移一位得到進位。

4、更新變量：將非進位和賦值給?num1，進位賦值給?num2，進行下一次迭代。

5、返回結果：當進位為0時，num1?即為最終的和，返回?num1。

使用位運算模擬二進制加法通過位運算高效地模擬了加法過程，避免了使用四則運算符號。

我們目前要寫出來C++的寫法是非常考驗前面C++的學習情況好不好的，大家可以嘗試去寫一寫，優先掌握C語言的寫法，博主還沒有介紹C++的算法題，之后會涉及的，敬請期待！

2.2? 找到所有數組中消失的數字

力扣鏈接：448. 找到所有數組中消失的數字

力扣題解鏈接：負號標記法解決【找到所有數組中消失的數字】問題

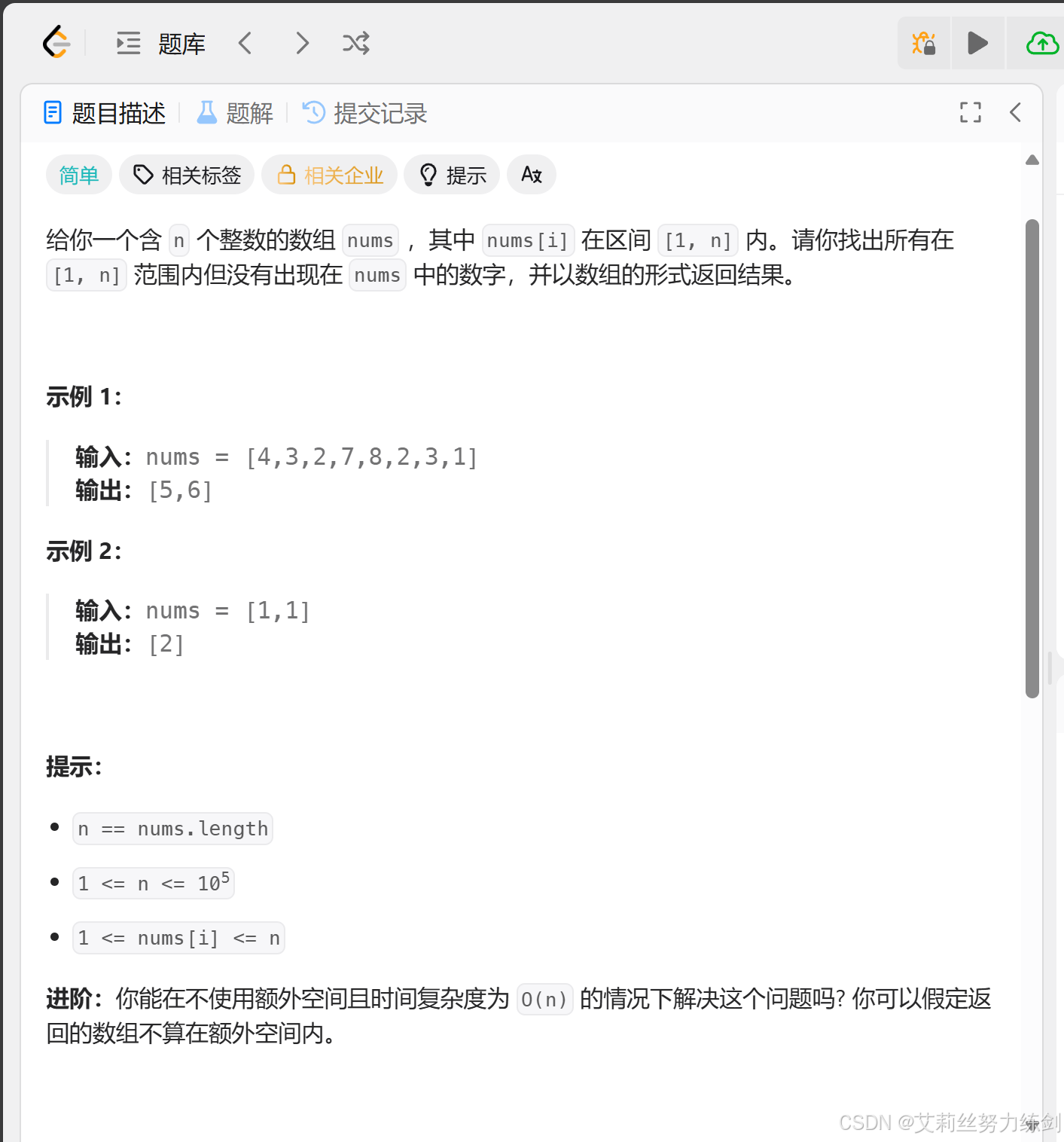
題目描述：

2.2.1 題目理解

題目的本質是：在一個長度為?n?的數組中，所有數字理論上都應該在?[1, n]?范圍內，但由于某些數字可能重復出現，導致其他數字缺失。我們需要找出所有缺失的數字。

本題中關鍵的約束條件——

1、數組長度 = n；

2、數字范圍 = [1, n]；

3、可能有重復數字；

4、需要找出所有缺失的數字。

2.2.2 思路

我們使用負號標記法，時間復雜度為 O(n)，空間復雜度為 O(1)（不考慮輸出數組）：

1、第一次遍歷：對于每個數字?nums[i]，我們將?nums[abs(nums[i])-1]?標記為負數；

2、第二次遍歷：所有仍然為正數的位置?i?表示數字?i+1?在原始數組中不存在。

這道題是接口型的，下面是C語言的模版（如果是IO型就可以不用管它們了）——

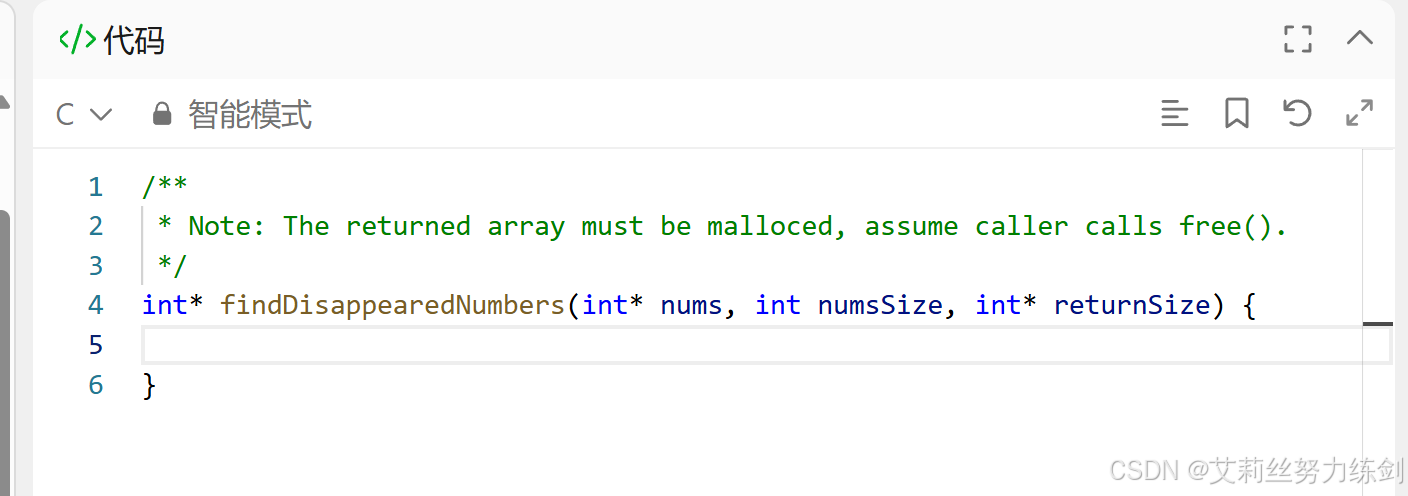
代碼演示：

//C語言實現——負號標記法
/*** Note: The returned array must be malloced, assume caller calls free().*/
int* findDisappearedNumbers(int* nums, int numsSize, int* returnSize) {// 第一次遍歷：使用負號標記法for (int i = 0; i < numsSize; i++) {int index = abs(nums[i]) - 1; // 獲取對應的索引位置if (nums[index] > 0) {nums[index] = -nums[index]; // 標記為負數表示該數字存在}}// 統計缺失的數字數量int count = 0;for (int i = 0; i < numsSize; i++) {if (nums[i] > 0) {count++;}}// 分配結果數組int* result = (int*)malloc(count * sizeof(int));*returnSize = count;// 第二次遍歷：收集缺失的數字int j = 0;for (int i = 0; i < numsSize; i++) {if (nums[i] > 0) {result[j++] = i + 1; // 索引+1就是缺失的數字}}return result;
}

時間復雜度：O(n)；

空間復雜度：O(1)。

我們學習了C++之后也可以嘗試用C++來實現一下，看看自己前段時間C++學得怎么樣——

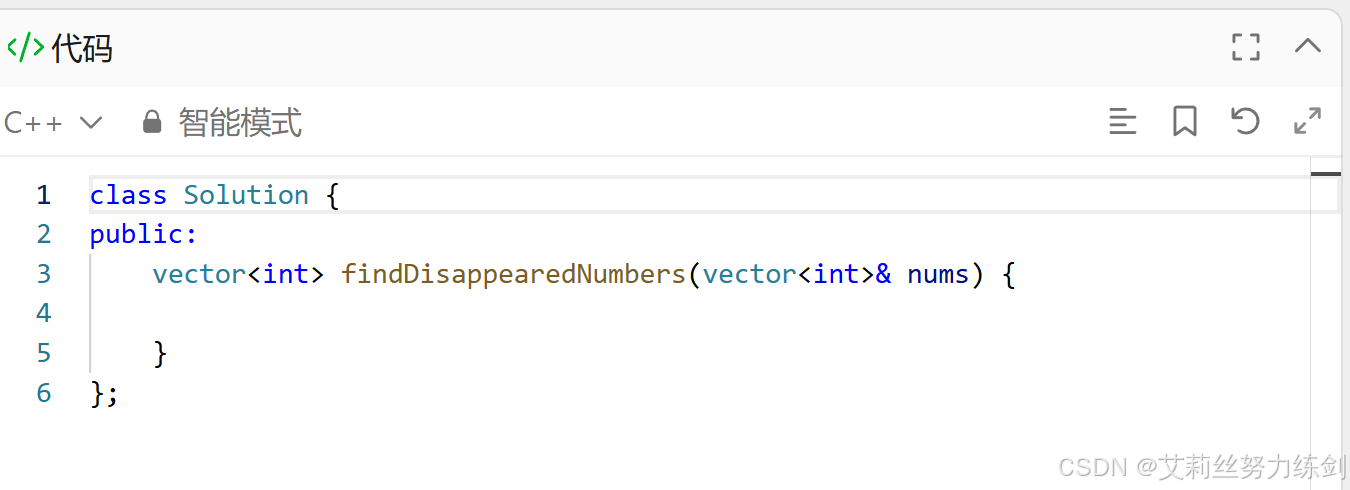
代碼演示：

//C++實現——負號標記法
class Solution {
public:vector<int> findDisappearedNumbers(vector<int>& nums) {int n = nums.size();// 使用負號標記法for (int i = 0; i < n; i++) {int index = abs(nums[i]) - 1; // 獲取對應的索引位置if (nums[index] > 0) {nums[index] = -nums[index]; // 標記為負數表示該數字存在}}vector<int> result;// 收集缺失的數字for (int i = 0; i < n; i++) {if (nums[i] > 0) {result.push_back(i + 1); // 索引+1就是缺失的數字}}return result;}
};

時間復雜度：O(n)，空間復雜度：O(1)。

我們可以用幾個示例來驗證一下——

對于輸入?[4, 3, 2, 7, 8, 2, 3, 1]：

（1）第一次遍歷后數組變為：[-4, -3, -2, -7, 8, 2, -3, -1]；

（2）位置4和5（索引從0開始）的值仍為正數，所以缺失的數字是5和6。

負號標記法這種方法高效且不需要額外的空間（除了輸出數組），非常適合處理大規模數據。

2.2.3? 為什么選擇負號標記法？

1、空間效率: 題目要求 O(1) 額外空間（不包括輸出數組）；

2、時間效率: 需要 O(n) 時間復雜度；

3、利用現有數組: 既然數字范圍是 [1, n]，我們可以用數組索引本身來記錄信息。

2.2.4? 負號標記法的巧妙之處

核心思想：用數組的索引位置來記錄數字是否存在。

具體操作：

（1）對于數字?x，我們去查看位置?x-1；

（2）如果該位置的值為正，我們就將其標記為負；

（3）這樣，最后仍然為正數的位置?i?就表示數字?i+1?不存在。

為什么這樣可行？

（1）因為數組索引從 0 到 n-1，正好對應數字 1 到 n；

（2）負號標記不會改變絕對值，所以不影響后續的判斷。

2.2.5? 與其他方法的對比

方法1：使用哈希表（不適用）

// 需要 O(n) 額外空間，不符合要求
unordered_set<int> seen;
for (int num : nums) seen.insert(num);
for (int i = 1; i <= n; i++) 
{if (!seen.count(i)) result.push_back(i);
}

方法2：排序后遍歷（不最優）

// 時間復雜度 O(n log n)，空間復雜度 O(1) 但修改了原數組
sort(nums.begin(), nums.end());
// 然后遍歷檢查缺失數字

方法3：負號標記法（最優）

1、時間復雜度: O(n) - 兩次遍歷；

2、空間復雜度: O(1) - 原地修改，無需額外空間；

3、保持信息: 通過負號標記，既記錄了存在性，又保留了原始值的絕對值。

結尾

本文內容到這里就全部結束了，希望大家練習一下這幾道題目，這些基礎題最好完全掌握！

往期回顧：

【C語言16天強化訓練】從基礎入門到進階：Day 9

【C語言16天強化訓練】從基礎入門到進階：Day 8

【C語言16天強化訓練】從基礎入門到進階：Day 7

【C語言16天強化訓練】從基礎入門到進階：Day 6

【C語言16天強化訓練】從基礎入門到進階：Day 5

【C語言16天強化訓練】從基礎入門到進階：Day 4

【C語言16天強化訓練】從基礎入門到進階：Day 3

【C語言16天強化訓練】從基礎入門到進階：Day 2

【C語言16天強化訓練】從基礎入門到進階：Day 1

結語：感謝大家的閱讀，記得給博主“一鍵四連”，感謝友友們的支持和鼓勵！