?
lc1976
dijk? ?min_path
pq. min_w
?
?
?
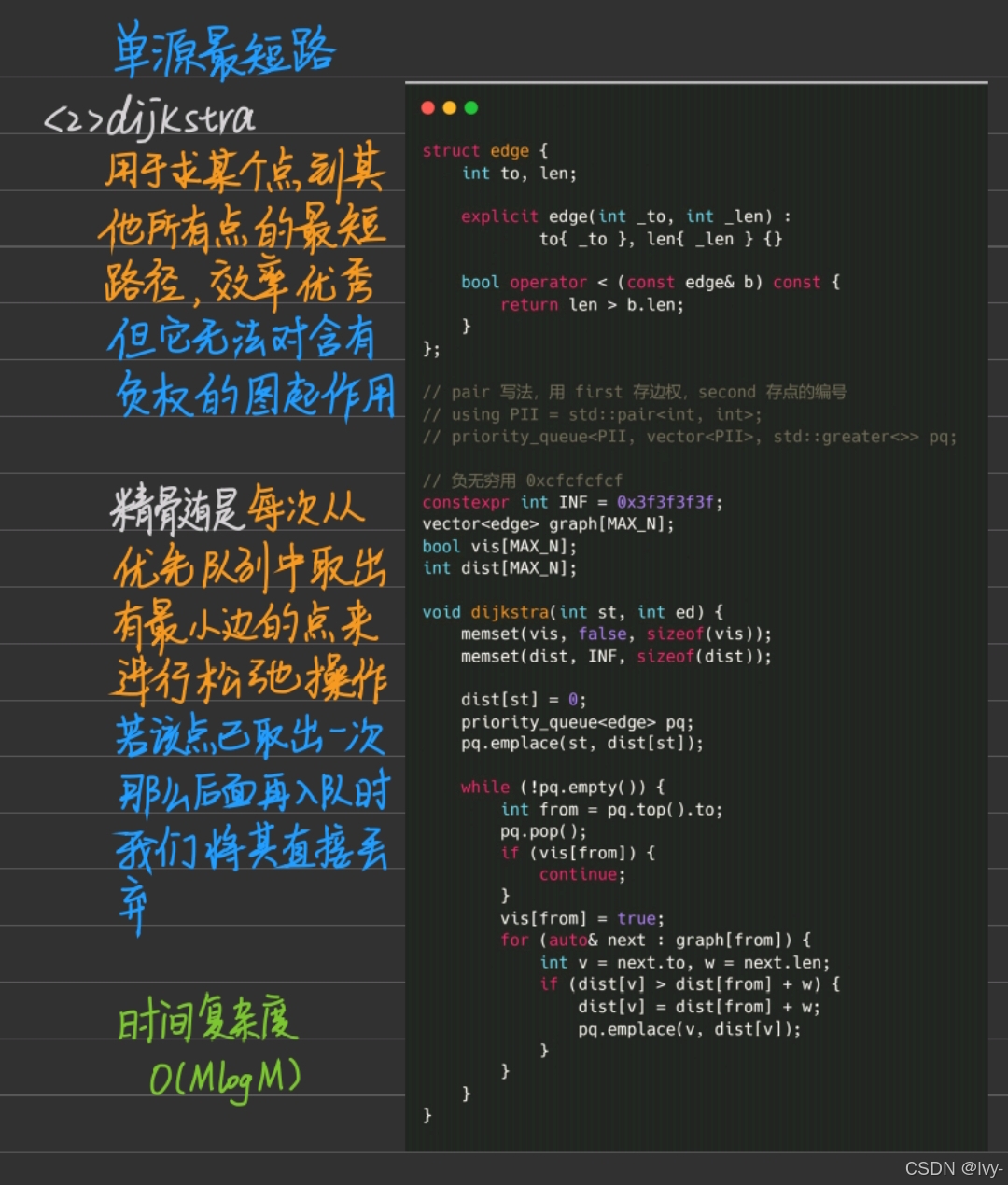
lcr187
同lc1823.約瑟夫環
class Solution {
public:
int iceBreakingGame(int num, int target)?
{
int x=0;
for(int i=2;i<=num;i++)
{
x=(x+target)%i;
} ? ?
return x;
}
};
?
lc2972
計算數組中可移除的子數組數量
先找最長遞增前綴，再結合遞增后綴統計符合條件的情況
class Solution {
typedef long long ll;
public:
long long incremovableSubarrayCount(vector<int>& a) {
int n = a.size();
int i = 0;
while (i < n - 1 && a[i] < a[i + 1]) {
i++;
}
if (i == n - 1) {
// 每個非空子數組都可以移除
return (ll)n * (n + 1) / 2;
}
??????? ll ans = i + 2;
// 不保留后綴的情況，一共 i+2 個
// 枚舉保留的后綴為 a[j:]
for (int j = n - 1; j == n - 1 || a[j] < a[j + 1]; j--) {
while (i >= 0 && a[i] >= a[j]) {
i--;
}
// 可以保留前綴 a[:i+1], a[:i], ..., a[:0] 一共 i+2 個
ans += i + 2;
}
return ans;
}
};
?
?
lcp02
倒著連分數，把“里面的分數”先算好，再一層層包進“外面的數”里。
? ? ? ? int up=1;
int down=0;
for(int i=cont.size()-1;i>=0;i--){
swap(up,down);? //up變分母后
up+=cont[i]*down;? //更新計算
}
return{up,down};
?
class Solution {
public:
vector<int> fraction(vector<int>& cont) {
int up=1;
int down=0;
for(int i=cont.size()-1;i>=0;i--){
swap(up,down);? //up變分母后
up+=cont[i]*down;? //更新計算
}
return{up,down};
}
};
?
?
左閉右開
?
lc153 無重復元素
?
class Solution {
public:
int findMin(vector<int>& nums)?
{
int n=nums.size();
int l=0,r=n-1;
while(l<r)
{
int mid=l+(r-l)/2;
if(nums[mid]>nums[r])
l=mid+1;
else
r=mid;
}
return nums[l];
}
};
?
lc154
二分法,左閉右開
當中間值和最右值相等時
右邊界r--? 左移一步，縮小范圍，排除重復元素干擾，最終找到最小值。
class Solution {
public:
int findMin(vector<int>& nums)?
{
int n = nums.size();
int l = 0, r = n - 1;
while (l < r) {
int mid = l + (r - l) / 2;
if (nums[mid] > nums[r])?
l = mid + 1;
? ? ? ? ? ?else if (nums[mid] < nums[r])?
// 右邊界更新為mid（保留mid可能為最小值的情況）
r = mid;
else?
r--;
}
return nums[l];
}
};
?
