棧和隊列：數據結構中的基礎與應用

在計算機科學的領域中，數據結構猶如大廈的基石，支撐著各類復雜軟件系統的構建。而棧和隊列作為兩種基礎且重要的數據結構，以其獨特的特性和廣泛的應用，在程序設計的舞臺上扮演著不可或缺的角色。

棧：“后進先出” 的存儲容器

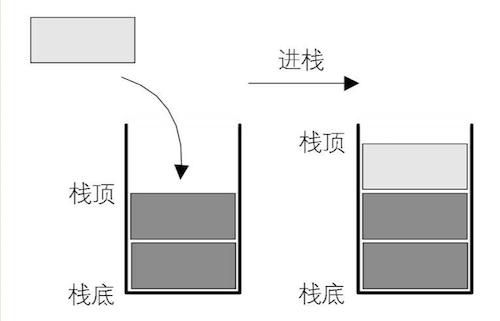
棧是一種特殊的線性表，其特殊性體現在操作的局限性上。它只允許在固定的一端進行數據的插入和刪除操作，這一端被稱為棧頂，另一端則是棧底 。這種操作限制使得棧呈現出 “先進后出”（LIFO，Last In First Out）的邏輯特性。在日常生活中，棧的身影隨處可見。比如堆疊的盤子，我們總是先取用最后放上去的盤子；函數調用時，最后調用的函數會最先返回；在文檔編輯軟件中，撤銷操作也是按照最近的修改最先被撤銷的順序進行 。

從實現方式來看，棧主要有順序棧和鏈式棧兩種。順序棧基于順序表實現，利用連續的內存空間來存儲元素，并通過管理結構體記錄棧的狀態，如棧的總容量、棧頂下標等。鏈式棧則借助單鏈表實現，每個鏈表節點存儲一個元素，同樣有管理結構體來維護棧頂指針、當前元素個數以及棧容量限制等信息 。

以順序棧的操作為例，初始化棧時，需要為存儲元素的數組分配內存空間，并將棧頂下標初始化為 -1，表示空棧。入棧操作時，首先判斷棧是否已滿，若未滿，則將棧頂下標加 1，然后在對應的數組位置存儲新元素。出棧操作則先檢查棧是否為空，若不為空，先獲取棧頂元素，再將棧頂下標減 1 。相關代碼實現如下：

// 順序棧結構體
typedef struct node {DATA *stack; // 存儲元素的數組首地址int size; // 棧的總容量int top; // 棧頂下標(初始為-1表示空棧)
}SeqStack;// 初始化棧
int sstack_init(SeqStack *s, int num) {s->data = (DATA *)calloc(num, sizeof(DATA));if(s->data == NULL) return -1;s->size = num;s->top = -1; return 0;
}// 數據入棧/壓棧
int sstack_push(SeqStack *s, DATA data) {if(sstack_isfull(s)) return -1;s->top++; s->data[s->top] = data; return 0;
}// 數據出棧/彈棧
int sstack_pop(SeqStack *s, DATA *data) {if(sstack_isempty(s)) return -1;*data = s->data[s->top];s->top--;return 0;
}

棧的優點顯著，操作簡單高效，由于僅對棧頂進行操作，其時間復雜度為 O (1) 。并且，“后進先出” 的特性使其在處理對稱性、嵌套性問題時得心應手。例如在表達式求值（中綴轉后綴）和括號匹配檢查中，棧能夠有效地解決這些問題。然而，棧也存在一定的局限性，它只能直接訪問棧頂元素，順序棧還存在容量限制，而鏈式棧則有額外的指針開銷 。

棧在實際應用中十分廣泛。在函數調用過程中，系統會利用棧來保存函數調用的相關信息，如返回地址、局部變量等，確保函數能夠正確地返回和執行 。在瀏覽器的前進后退功能中，同樣運用了棧的原理，用戶訪問過的頁面地址被依次壓入棧中，通過對棧的操作實現前進和后退的功能 。

隊列：“先進先出” 的有序序列

隊列同樣是一種特殊的線性表，它的特殊之處在于只能在固定的兩端進行操作，一端用于插入元素，稱為隊尾；另一端用于刪除元素，稱為隊頭 。這種操作方式使得隊列呈現出 “先進先出”（FIFO，First In First Out）的特性，與現實生活中的排隊現象極為相似。例如在銀行排隊辦理業務，先來的客戶先接受服務；打印隊列中，先提交的文檔先被打印；消息隊列里，先到達的消息先被處理 。

隊列的存儲實現主要有循環隊列和鏈式隊列。循環隊列基于數組實現，通過巧妙的模運算實現了數組空間的循環利用。為了區分隊空和隊滿的狀態，通常會犧牲一個存儲單元 。鏈式隊列則借助鏈表節點存儲元素，通過維護隊頭指針和隊尾指針來管理隊列 。

以循環隊列的操作為例，初始化循環隊列時，需要為存儲數組分配內存空間，并將隊頭下標和隊尾下標都初始化為 0 。入隊操作時，先判斷隊列是否已滿，若未滿，則在隊尾下標對應的數組位置存儲新元素，然后更新隊尾下標 。出隊操作則先檢查隊列是否為空，若不為空，先獲取隊頭元素，再更新隊頭下標 。相關代碼實現如下：

// 循環隊列結構體
typedef struct {DATA *data; // 存儲數組int size; // 隊列容量int front; // 隊頭下標(出隊維護隊頭下標)int rear; // 隊尾下標(入隊維護隊尾下標)
}SQueue;// 初始化循環隊列
int squeue_init(SQueue *q, int size) {q->data = (DATA *)calloc(size, sizeof(DATA));if (q->data == NULL)return -1;q->size = size;q->front = q->rear = 0;return 0;
}// 元素入隊
int squeue_enqueue(SQueue *q, DATA data) {if (squeue_isfull(q))return -1;q->data[q->rear] = data;q->rear = (q->rear + 1) % q->size; return 0;
}// 元素出隊
int squeue_dequeue(SQueue *q, DATA *data) {if (squeue_isempty(q))return -1;*data = q->data[q->front];q->front = (q->front + 1) % q->size;return 0;
}

隊列的優點在于 “先進先出” 的特性保證了操作的公平性，并且支持高效的隊頭和隊尾操作 。循環隊列在訪問速度上具有優勢，適合固定大小場景；鏈式隊列則能動態擴容，適用于大小不確定的場景 。但隊列也有其缺點，它只能直接訪問隊頭和隊尾元素，循環隊列還存在固定容量限制 。

隊列在眾多領域有著廣泛的應用。在任務調度中，如打印隊列，能夠按照任務提交的先后順序依次執行任務 。在消息隊列中，確保消息按照到達的先后順序被處理，避免消息混亂 。在廣度優先搜索（BFS）算法中，隊列用于存儲待訪問的節點，保證了搜索的廣度優先特性 。在緩沖池管理和多線程編程中的生產者 - 消費者模式中，隊列也發揮著重要作用，實現了數據的有序傳遞和共享 。

亂 。在廣度優先搜索（BFS）算法中，隊列用于存儲待訪問的節點，保證了搜索的廣度優先特性 。在緩沖池管理和多線程編程中的生產者 - 消費者模式中，隊列也發揮著重要作用，實現了數據的有序傳遞和共享 。

棧和隊列作為基礎的數據結構，雖然看似簡單，卻蘊含著強大的功能和廣泛的應用價值。它們為解決各種復雜的編程問題提供了有效的工具和思路，無論是在系統軟件的底層實現，還是在應用軟件的功能開發中，都占據著舉足輕重的地位 。深入理解和熟練運用棧和隊列，將為我們在計算機科學的道路上奠定堅實的基礎 。