生成函數

概念

又稱母函數把一個無窮數列 {an}\{a_n\}{an?}（默認從 $0$ 項起）表示成 $G(x)=\sum _{i\ge 0}{a}_i{x}^i$ 的函數形式。例如：

• $a_i=2^i$：$G(x)=\sum _{i\ge 0}{2}^i{x}^i$；
• $a_i=1$：$G(x)=\sum _{i\ge 0}{x}^i$。

應用

用來幫助推導數列的通項公式（比如斐波那契數列）也可以作為條件形式以數列形式給出的象征。一個特別的轉化：逆運用等比數列求和公式，可以得到：$\frac{1}{1?ax}=\sum _{i\ge 0}{a}^i{x}^i$，等號左邊不帶求和符號部分的，稱為生成函數的封閉形式。

生成函數的乘法運算有意義，其卷積形式是函數直接相乘。對于 $A(x)=\sum _{i\ge 0}{a}_i{x}^i$ 和 $A(x)=\sum _{i\ge 0}{b}_i{x}^i$：
$$A\times B=\sum _{i\ge 0}^n\left(x^i\sum _{j=0}^i{a}_j{b}_{i?j}\right)$$

洛谷 P10780 BZOJ3028 食物

題意

題目傳送門。

思路

根據上文，將這個背包問題轉化為，考慮每一種物品拿的個數的生成函數，并用封閉形式表示：

• 偶數個形如 {1,0,1,0,1,......}\{1,0,1,0,1,......\}{1,0,1,0,1,......}：$\sum _{k\ge 0}{x}^{2k}=\frac{1}{1?x^2}$；
• $0$ 或 $1$ 個形如 {1,1,0,0,0,......}\{1,1,0,0,0,......\}{1,1,0,0,0,......}：$1+x$；
• $0$ 或 $1$ 或 $2$ 個形如 {1,1,1,0,0,......}\{1,1,1,0,0,......\}{1,1,1,0,0,......}：$1+x+x^2$；
• 奇數個形如 {0,1,0,1,0,......}\{0,1,0,1,0,......\}{0,1,0,1,0,......}：$\sum _{k\ge 0}{x}^{2k+1}=x\sum _{k\ge 0}{x}^{2k}=\frac{x}{1?x^2}$；
• $4$ 的倍數個類似第一條：$\sum _{k\ge 0}{x}^{4k}=\frac{1}{1?x^4}$；
• $0$ 或 $1$ 或 $2$ 或 $3$ 個形如 {1,1,1,0,0,......}\{1,1,1,0,0,......\}{1,1,1,0,0,......}：$1+x+x^2+x^3$；
• $3$ 的倍數個類似第一條：$\sum _{k\ge 0}{x}^{3k}=\frac{1}{1?x^3}$.

全部乘起來，并用二項式定理化簡 $1+x+x^2$ 和 $1+x+x^2+x^3$：
$$\frac{x}{(1?x{)}^4}$$

考慮推 $\frac{1}{(1?x{)}^k}={\left(\frac{1}{1?x}\right)}^k$ 是哪個生成函數的封閉形式與該生成函數的第 $n$ 項系數，因為 $\frac{1}{1?ax}=\sum _{i\ge 0}{a}^i{x}^i$，$a=1$ 時，$\frac{1}{1?x}=1+x+x^2+x^3+...$。$k$ 次方展開后，相當于選 $k$ 個自然數和為 $n$ 的方案數：先給 $k$ 個數加 $1$ 轉化問題為 $k$ 個正整數和為 $n+k$，運用插板法得知方案數為 $\left(\genfrac{}{}{0ex}{}{n+k?1}{k?1}\right)$。

回到這一題 $\frac{1}{(1?x{)}^4}$ 的第 $n?1$ 項系數為 $\left(\genfrac{}{}{0ex}{}{n?2}{3}\right)$，乘回 $x$ 后即為答案。代碼略。

Polya 計數

等我完全理解完再回來補。先給結論：用 $k$ 中顏色給 $n$ 個點的環染色方案數為 $\frac{1}{n}\sum _{i=0}^{n?1}{k}^{\gcd (n,i)}$，可否感性理解呢？

洛谷 P4980 【模板】Pólya 定理

題意

用 $n$ 種顏色給 $n$ 個點染色的方案數。兩種方案相同，當且僅當一種方案能夠旋轉變為“另一方案”。

$n\le 10^9$。

思路

問題是如何快速算出 $\frac{1}{n}\sum _{i=0}^{n?1}{n}^{\gcd (n,i)}$。不妨暴力枚舉 $n$ 的約數 $d=\gcd (n,i)$，變為：
$$\frac{1}{n}\sum _{d|n}{n}^d\phi (\frac{n}{d})$$

$n$ 太大了不能預處理 $\phi$，記得勤取模。時間復雜度為 T(n)=∑i≥0{O(i)+O(n/i)}=O(n3/4)T(n)=\displaystyle\sum_{i\ge 0}\{O(\sqrt{i})+O(\sqrt{n/i})\}=O(n^{3/4})T(n)=i≥0∑?{O(i?)+O(n/i?)}=O(n3/4)（根據主定理推得）。代碼略。

第二類斯特林數

為什么先說第二類，因為第二類好像常用一些。

斯特林數將兩個典型的模型的方案數求解變成一個類似組合數的東西。

概念

$\left\{\begin{array}{c}n\\ m\end{array}\right\}$ 表示，將 $n$ 個不同的球放進 $m$ 個相同的盒子里，且每個盒子都非空的方案數。

其遞推式的推導：

• 球 $n$ 單開一個盒子，那么剩下 $n?1$ 個球放進 $m?1$ 個盒子：$\left\{\begin{array}{c}n?1\\ m?1\end{array}\right\}$；
• 球 $n$ 放進非空的 $m$ 個盒子：$m\left\{\begin{array}{c}n?1\\ m\end{array}\right\}$。

所以 $\left\{\begin{array}{c}n\\ m\end{array}\right\}=\left\{\begin{array}{c}n?1\\ m?1\end{array}\right\}+m\left\{\begin{array}{c}n?1\\ m\end{array}\right\}$。

特別的，$\left\{\begin{array}{c}n\\ 0\end{array}\right\}=[n=0]$，中括號表示艾弗森括號。

可以 $O(n^2)$ 預處理。

應用

先證明其通項公式，發現其滿足下降冪性質：

CF932E Team Work

題意

給定 $n,k$，求 $\sum _{i=1}^n\left(\genfrac{}{}{0ex}{}{n}{i}\right)i^k$。

$n\le 10^9$，$k\le 5000$。

思路

把組合數用階乘拆開，再運用斯特林數下降冪的性質：

$$\sum _{i=0}^n\frac{n!}{i!(n?i)!}\sum _{j=0}^k\left\{\begin{array}{c}k\\ j\end{array}\right\}\frac{i!}{(i?j)!}$$

改變 $i$ 和 $j$ 的枚舉順序，$i$ 從 $j$ 開始到 $n$：
$$\sum _{j=0}^k\left\{\begin{array}{c}k\\ j\end{array}\right\}\sum _{i=j}^n\frac{n!}{(n?i)!(i?j)!}$$

強制變成組合數：
$$\sum _{j=0}^k\left\{\begin{array}{c}k\\ j\end{array}\right\}\frac{n!}{(n?j)!}\sum _{i=j}^n\frac{(n?j)!}{(n?i)!(i?j)!}$$

$$\sum _{j=0}^k\left\{\begin{array}{c}k\\ j\end{array}\right\}\frac{n!}{(n?j)!}\sum _{i=j}^n\left(\genfrac{}{}{0ex}{}{n?j}{i?j}\right)$$

化成 $2$ 次冪形式：
$$\sum _{j=0}^k\left\{\begin{array}{c}n\\ m\end{array}\right\}\frac{n!}{(n?j)!}\sum _{i=0}^{n?j}\left(\genfrac{}{}{0ex}{}{n?j}{i}\right)$$

$$\sum _{j=0}^k\left\{\begin{array}{c}k\\ j\end{array}\right\}\frac{n!}{(n?j)!}\times 2^{n?j}$$

$O(k^2)$ 時間復雜度預處理第二類斯特林數即可。

代碼

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=5002,mod=1e9+7;
ll n,k;
ll S2[N][N],p2[N];
ll qpow(ll x,ll k)
{ll ret=1;while(k){if(k&1)ret=ret*x%mod;x=x*x%mod;k>>=1;}return ret;
}
void init()
{S2[0][0]=1;for(int i=1;i<N;i++)for(int j=1;j<N;j++)S2[i][j]=(S2[i-1][j-1]+j*S2[i-1][j]%mod)%mod;
}
int main()
{scanf("%lld%lld",&n,&k);init();ll ans=0;for(int j=0;j<=min(n,k);j++){ll ret=S2[k][j]*qpow(2,n-j)%mod,mul=1;for(int t=n-j+1;t<=n;t++)ret=ret*t%mod;ans=(ans+ret)%mod;}printf("%lld",ans);return 0;
}

第一類斯特林數

概念

$\left[\begin{array}{c}n\\ m\end{array}\right]$ 表示，將 $n$ 個不同的球擺成 $m$ 個環的方案數。兩個環相同，當且僅當一個環通過旋轉可以變成第二個環。

其遞推式的推導：

• 球 $n$ 單開一個環，那么剩下 $n?1$ 個球成 $m?1$ 個環：$\left[\begin{array}{c}n?1\\ m?1\end{array}\right]$；
• 球 $n$ 放進 $m$ 個環，在放了的 $(n?1)$ 個球后面都可以放：$(n?1)\left[\begin{array}{c}n?1\\ m\end{array}\right]$。

所以 $\left[\begin{array}{c}n\\ m\end{array}\right]=\left[\begin{array}{c}n?1\\ m?1\end{array}\right]+(n?1)\left[\begin{array}{c}n?1\\ m\end{array}\right]$。

特別的，$\left[\begin{array}{c}n\\ m\end{array}\right]=[n=0]$，中括號為艾弗森括號。

洛谷 P4609 FJOI2016 建筑師

題意

小 Z 是一個很有名的建筑師，有一天他接到了一個很奇怪的任務：在數軸上建 $n$ 個建筑，每個建筑的高度是 $1$ 到 $n$ 之間的一個整數。

小 Z 有很嚴重的強迫癥，他不喜歡有兩個建筑的高度相同。另外小 Z 覺得如果從最左邊（所有建筑都在右邊）看能看到 $A$ 個建筑，從最右邊（所有建筑都在左邊）看能看到 $B$ 個建筑，這樣的建筑群有著獨特的美感。現在，小 Z 想知道滿足上述所有條件的建筑方案有多少種？

如果建筑 $i$ 的左(右)邊沒有任何建造比它高，則建筑 $i$ 可以從左(右)邊看到。兩種方案不同，當且僅當存在某個建筑在兩種方案下的高度不同。

$1\le n\le 50000,1\le A,B\le 100,1\le T\le 200000$。

思路

中間那個左右都能看見的，高度必然是極值 $n$。

除去中間的，左邊要看到 $a?1$ 個，右邊要看到 $b?1$ 個。不妨將能看到的和其左/右邊比它矮的看成 $a?1+b?1=a+b?2$ 個環（反正互換位置之后，盡管某些環的元素種類改變，但是環的個數不改變），就可以用第一類斯特林數的含義，將剩下 $n?1$ 和分成 $a+b?2$ 個環，即 $\left[\begin{array}{c}n?1\\ a+b?2\end{array}\right]$。

然后再 $a+b?2$ 個環中選各自最大值 $a?1$ 個，成為左邊能看見的（排列方式唯一，必然是從矮到高），即 $\left(\genfrac{}{}{0ex}{}{a+b?2}{a?1}\right)$。

于是答案為 $\left[\begin{array}{c}n?1\\ a+b?2\end{array}\right]\left(\genfrac{}{}{0ex}{}{a+b?2}{a?1}\right)$。

預處理第一類斯特林數即可。

代碼

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=5e4+9,M=202,mod=1e9+7;
ll T;
ll S1[N][M],fac[N],inv[N];
ll qpow(ll x,ll k)
{ll ret=1;while(k){if(k&1)ret=ret*x%mod;x=x*x%mod;k>>=1;}return ret;
}
void init()
{S1[0][0]=1;for(int i=1;i<N;i++)for(int j=1;j<M;j++)S1[i][j]=(S1[i-1][j-1]+(i-1)*S1[i-1][j]%mod)%mod;fac[0]=1;for(int i=1;i<N;i++)fac[i]=fac[i-1]*i%mod;inv[N-1]=qpow(fac[N-1],mod-2);for(int i=N-2;i>=0;i--)inv[i]=inv[i+1]*(i+1)%mod;
}
ll C(ll n,ll m)
{return fac[n]*inv[m]%mod*inv[n-m]%mod;
}
int main()
{scanf("%lld",&T);init();while(T--){ll n,a,b;scanf("%lld%lld%lld",&n,&a,&b);printf("%lld\n",S1[n-1][a+b-2]*C(a+b-2,a-1)%mod);}return 0;
}

無根樹的 prufer 序列

概念

prufer 序列將節點數為 $n$ 的無根樹轉化為長為 $n?2$ 的序列。其表示期望與根的編號無關——定義為每次選擇一個編號最小的葉節點并刪除，然后在序列中記錄其所連接的節點編號，直到剩下兩個節點。

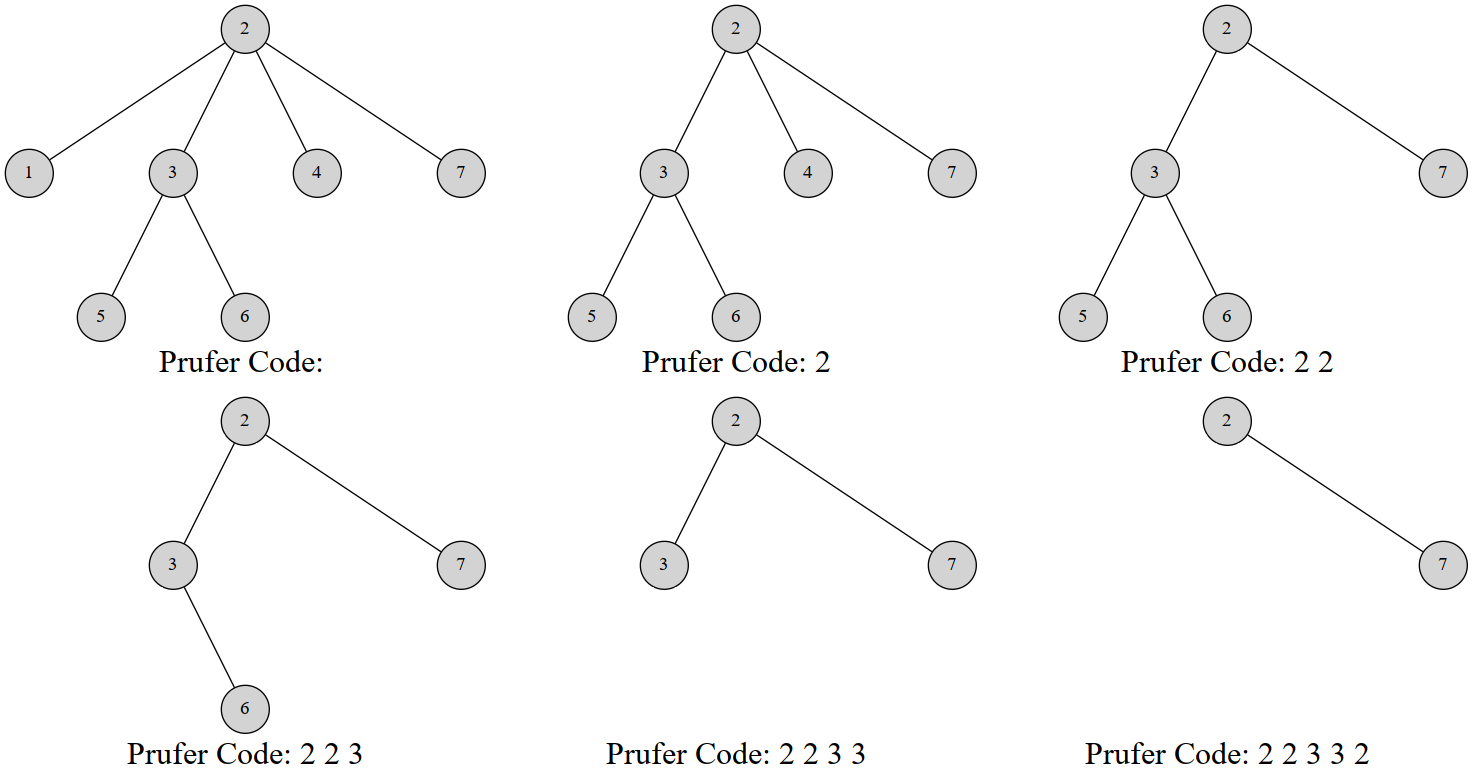
如上圖是一棵有 $7$ 個節點的樹的 prufer 序列形成過程。

用 prufer 序列同樣可以還原出一棵樹來。

求法

求一棵樹的 prufer 序列。可以維護每個節點的度數，以節點編號為第一關鍵字扔進堆里排序，當度為 $0$ 時舍棄這個節點。容易做到 $O(n\log n)$。

有 $O(n)$ 的更優秀的算法：“剝葉子”的過程中，每次只會讓其父親節點度數減 $1$，因此每刪除一個葉節點，至多產生一個新葉節點。

因此可以用一個單調指針 $pos$ 維護當前度數為 $0$ 的最小結點，$pos$ 枚舉到了先刪 $pos$，然后看 $f{a}_{pos}$ 是否度數變為 $0$，如果為 $0$ 就順帶刪去了；沒準是條鏈，因此可以 while 一路刪上去。

用 prufer 還原一棵樹維護序列中節點的待加邊，當兒子連完、待加邊歸 $0$，就連向序列中下一個節點——似乎完全就是求 prufer 的相反操作，具體看下面的代碼。

P6086 【模板】Prufer 序列

思路

如上所述。

代碼

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=1e5+9;
ll n,m,mod,k;
ll fa[N],siz[N];
ll fz(ll x)
{while(x!=fa[x])x=fa[x]=fa[fa[x]];return x;
}
void join(ll u,ll v)
{ll fu=fz(u),fv=fz(v);if(fu==fv)return;fa[fu]=fv;siz[fv]+=siz[fu];k--;
}
ll qpow(ll x,ll k)
{ll ret=1;while(k){if(k&1)ret=ret*x%mod;x=x*x%mod;k>>=1;}return ret;
}
int main()
{scanf("%lld%lld%lld",&n,&m,&mod);if(mod==1){puts("0");return 0;}k=n;for(int i=1;i<=n;i++)fa[i]=i,siz[i]=1;for(int i=1;i<=m;i++){ll u,v;scanf("%lld%lld",&u,&v);join(u,v);}if(k==1){puts("1");return 0;}ll ans=1;for(int i=1;i<=n;i++)if(i==fz(i))ans=ans*siz[i]%mod;ans=ans*qpow(n,k-2)%mod;printf("%lld",ans);return 0;
}

prufer 序列怎么求其實應用不廣，關鍵是其本身所帶有的性質更為重要。

應用

• 把一個樹化為 prufer 序列，是建立 $n$ 個節點無根樹和 $n?2$ 個元素的序列的雙射。

• 一個節點在 prufer 序列中出現次數為其度數減 $1$；

• Cayley 公式：對 $n$ 個節點建立一棵無根樹，有 $n^{n?2}$ 種方案。

  證明：任意一個長度為 $n?2$ 的值域 $[1,n]$ 的整數序列都可以通過 prufer 序列雙射對應一個生成樹，于是方案數就是 $n^{n?2}$。

CF156D Clues

題意

給定一個 $n$ 個點 $m$ 條邊的帶標號無向圖，若其有 $k$ 個連通塊，想要添加 $k?1$ 條邊使得整個圖連通。求方案數。

$1\le n\le 10^5$，$0\le m\le 10^5$，$1\le k\le 10^9$。

思路

這是一道經典問題。

設每個連通塊有 $s_i$ 個節點，$d_i$ 為連通塊的度數—— prufer 序列就是用度數所推。

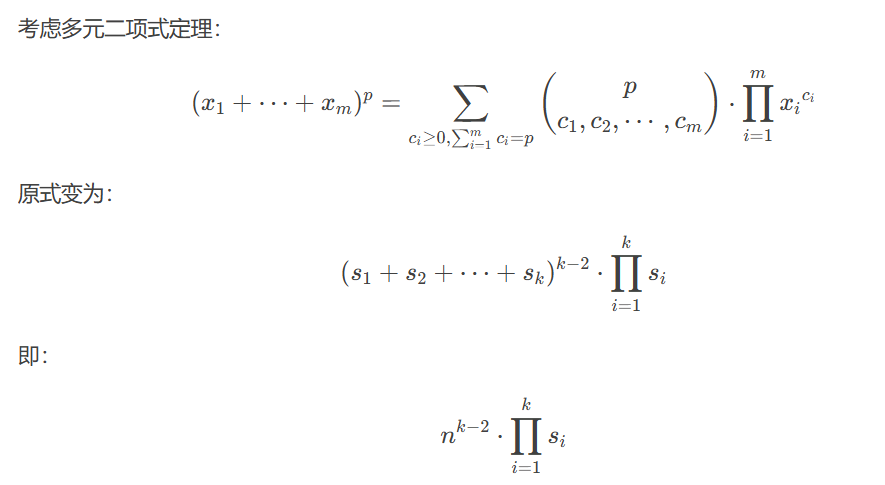
計算上式即可。代碼略。

洛谷 P2290 HNOI2004 樹的計數

題意

一個有 $n$ 個節點的樹，設它的節點分別為 $v_1,v_2,\dots ,v_n$，已知第 $i$ 個節點 $v_i$ 的度數為 $d_i$，問滿足這樣的條件的不同的樹有多少棵。

$1\le n\le 150$，保證滿足條件的樹不超過 $10^{17}$ 個。

思路

其實方案數就是上一篇題解所提，$\left(\genfrac{}{}{0ex}{}{n?2}{d_1?1,d_2?1,d_3?1,......,d_n?1}\right)=\frac{(n?2)!}{\prod _{i=1}^n(d_i?1)!}$。

好像會爆 long long，階乘的增長速度超乎想象，倒不如用它的普通組合數意義形式。設 $s_i=d_i?1$，$sum=n?2$（理論上是 $\sum s_i$，如果不是就不合法）。答案就是 $$\prod _{i=1}^n\left(\genfrac{}{}{0ex}{}{sum?\sum _{j=1}^{i?1}{s}_j}{s_i}\right)$$

代碼略。

洛谷 P2624 HNOI2008 明明的煩惱

題意

給出標號為 $1$ 到 $n$ 的點，以及某些點最終的度數，允許在任意兩點間連線，可產生多少棵度數滿足要求的樹？無解就輸出 $?1$。

$1\le n\le 1000$。

思路

這是上一題的加強版。

對于已知的 $m$ 個點，我們可以直接套用上面的 $\left(\genfrac{}{}{0ex}{}{m?2}{d_1?1,d_2?1,d_3?1,......,d_m?1}\right)=\frac{(m?2)!}{\prod _{i=1}^m(d_i?1)!}$ 公式，prufer 序列上已經選了的方案數為 $\left(\genfrac{}{}{0ex}{}{n?2}{\sum _{i=1}^m(d_i?1)}\right)$，最后再把剩下的 $n?m$ 個點，塞進 $n?2?\sum _{i=1}^m(d_i?1)$ 去：
$$\left(\genfrac{}{}{0ex}{}{n?2}{\sum _{i=1}^m(d_i?1)}\right)\frac{(m?2)!}{\prod _{i=1}^m(d_i?1)!}\times (n?m{)}^{n?2?\sum _{i=1}^m(d_i?1)}$$

沒得化回普通組合數，要用高精捏。代碼略，有緣再寫。