密碼學系列文(3)--分組密碼

一、分組密碼概述

分組密碼是許多系統安全的一個重要組成部分，可用于構造：

擬隨機數生成器
流密碼
消息認證碼(MAC)和雜湊函數
消息認證技術、數據完整性機構、實體認證協議以及單鑰數字簽字體制的核心組成部分

應用中對于分組密碼的要求：

安全性
運行速度
存儲量（程序的長度、數據分組長度、高速緩存大小）
實現平臺（硬、軟件、芯片）
運行模式

明文序列 $x_1,x_2,...,x_i,...$

加密函數 $E:V_n\times K\rightarrow V_n$

這種密碼實質上是字長為 $m$ 的數字序列的代換密碼;如圖所示：

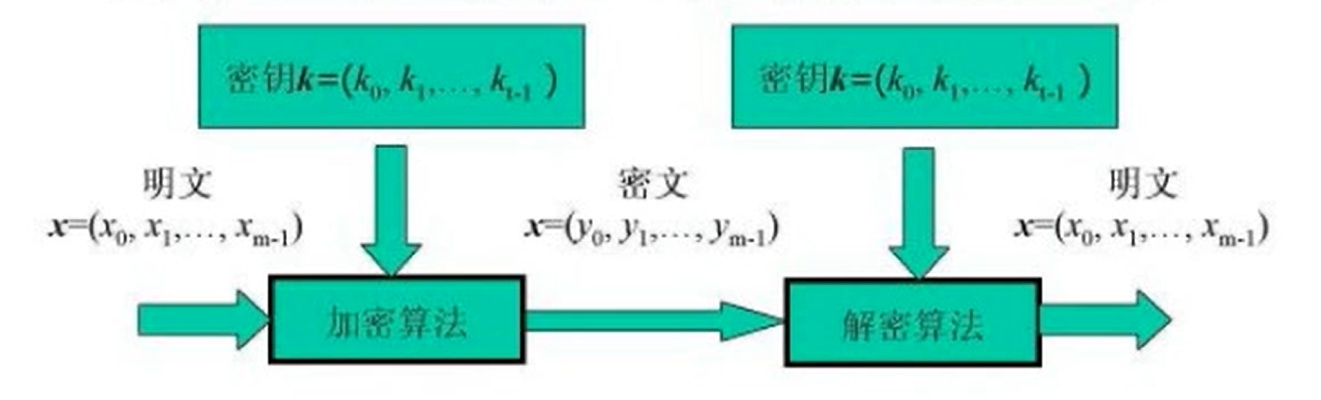
通常取 $n=m$ ；

若 $n>m$ ，則為有數據擴展的分組密碼；

若 $n<m$ ，則為有數據壓縮的分組密碼；

分組密碼的設計問題在于找到一種算法，能在密鑰控制下從一個足夠大且足夠好的置換子集中，簡單而迅速地選出一個置換，用來對當前輸入的明文的數字組進行加密變換。

分組密碼算法應滿足的要求：

分組長度n要足夠大：防止明文窮舉攻擊法奏效；
密鑰量要足夠大：盡可能消除弱密鑰并使所有密鑰同等地好，以防止密鑰窮舉攻擊奏效；
由密鑰確定置換的算法要足夠復雜：充分實現明文與密鑰的擴散和混淆，沒有簡單的關系可循，要能抗擊各種已知的攻擊；
加密和解密運算簡單：易于軟件和硬件高速實現；
數據擴展：一般無數據擴展，在采用同態置換和隨機化加密技術時可引入數據擴展；
差錯傳播盡可能地小

1.1 代換網絡

代換是輸入集 $A$ 到輸出 $A'$ 上的雙射變換: $f_k:A\rightarrow A'$ 。式中， $k$ 是密鑰。
實現代換 $f_k$ 的網絡稱作代換網絡。雙射條件保證在給定 $k$ 下可從密文唯一地恢復出原明文。
代換 $f_k$ 的集合： $S=\left \{ f_k|k\in K \right \}$ , $K$ 是密鑰空間。如果網絡可以實現所有可能的 $2^n!$ 個代換，則稱其為全代換網絡。全代換網絡密鑰個數必須滿足條件： $\left \{ k \right \}\geq 2^n!$ .
密碼設計中需要先定義代換集 $S$ ，而后還需定義解密變換集，即逆代換網絡 $S^{-1}$ ，它以密文 $y$ 作為輸入矢量，其輸出為恢復的明文矢量 $x$
要實現全代換網絡并不容易。因此實用中常常利用一些簡單的基本代換，通過組合實現較復雜的、元素個數較多的代換集。實現密碼體制的集合 $S$ 中的元素個數都遠小于 $2^n!$

1.2 代換盒(S盒)?

在密碼設計中，可選 $n=r\cdot n_0$ ，其中 $r$ 和 $n_0$ 都為正整數，將設計 $n$ 個變量的代換網絡化為設計 $r$ 個較小的子代換網絡，而每個子代換網絡只有 $n_0$ 個輸入變量。稱每個子代換網絡為代換盒(Substitution Box)

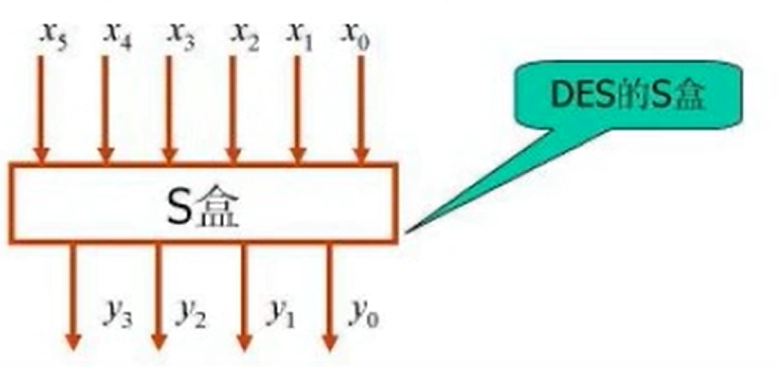
$DES$ 的 $S_1$ 盒的輸入和輸出關系:

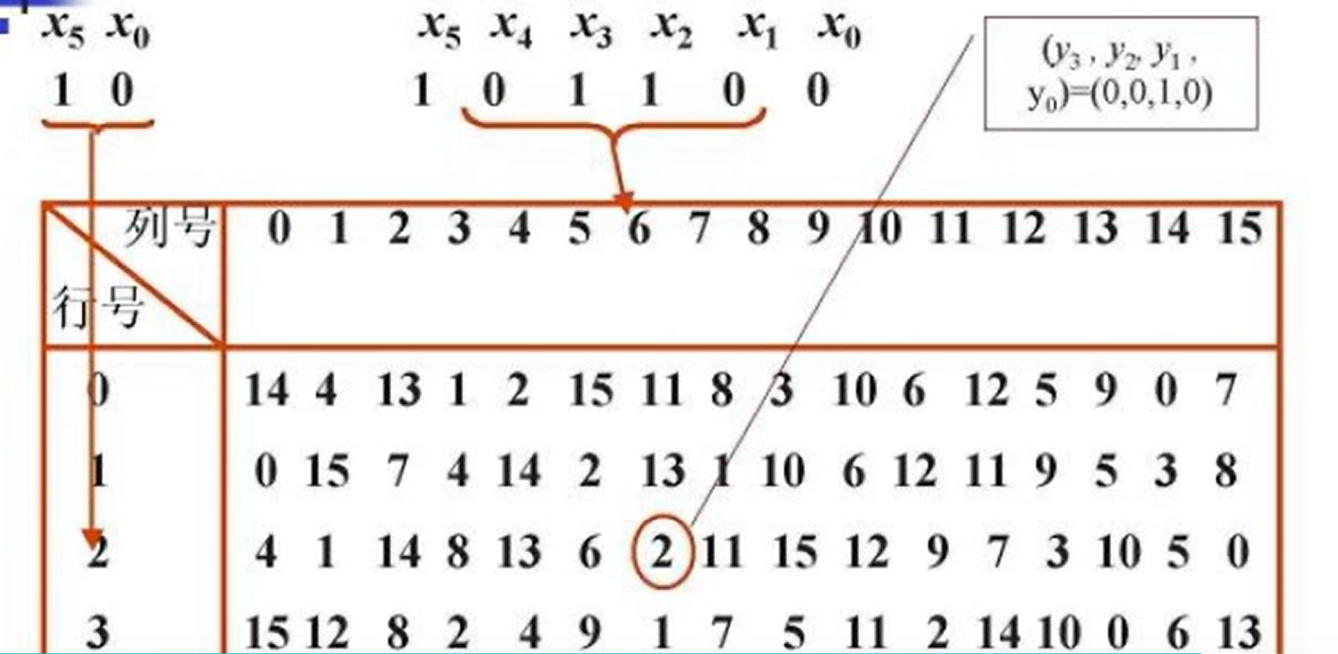
1.3 擴散和混淆

擴散將明文的統計特征散步到密文中。實現的方式是使明文的每一位影響密文中多位的值。
混淆是使密文和密鑰之間的統計關系變得盡可能復雜，以使敵手無法得到密鑰。因此即使敵手能得到密文的一些統計關系，由于密鑰和密文之間統計關系復雜化，敵手無法得到密鑰。

擴散和混淆成功地實現了分組密碼的本質屬性，因而成為設計現代分組密碼的基礎。

S盒的設計準則實現較好的混淆：

S盒的輸出都不是其輸入的線性或仿射函數；
改變S盒的一個輸入比特，其輸出至少有兩比特產生變化，即近一半產生變化；
當S盒的任一輸入位保持不變，其它5位輸入變化時(共有 $2^5=32$ 種情況),輸出數字中的0和1的總數近于相等；

S盒的組合（將幾個S盒組合起來構成一個n值較大的組）：

將幾個S盒的輸入端并行，并通過坐標置換(P盒)將各S盒輸出比特次序打亂，再送到下一級各S盒的輸入端，起到了Shannon所謂的“擴散”作用。
S盒提供非線性變換，將來自上一級不同的S盒的輸出進行混淆。經過P盒的擴散作用使1均勻分散到整個輸出矢量中，從而保證了輸出密文統計上的均勻性，這就是Shannon的乘積密碼的作用。

1.4 Feistel網絡

將n比特明文分成為左右各半，長為 $\frac{n}{2}$ 比特的段，以 $L$ 和 $R$ 表示。然后進行多輪迭代，其第 $i$ 輪迭代的輸出為前輪輸出的函數：

$L_i=R_{i-1}$
$R_i=L_{i-1}\bigoplus f(R_{i-1},K_i)$

式中， $K_i$ 是第 $i$ 輪用的子密鑰， $f$ 是任意密碼輪函數。稱這種分組密碼算法為Feistel網絡，它保證加密和解密可采用同一算法實施。

1.5 迭代分組密碼

若以一個簡單函數 $f$ ，進行多次迭代，就稱其為迭代密碼

每次迭代稱作一輪(Round)，相應函數 $f$ 稱作輪函數

每一輪輸出都是前一輪輸出的函數，即 $y^{(i)}=f(y^{(i-1)},k^{(i)})$ ，其中 $k^{(i)}$ 是第 $i$ 輪迭代用的子密鑰，由秘密密鑰 $k$ 通過密鑰生成算法產生；

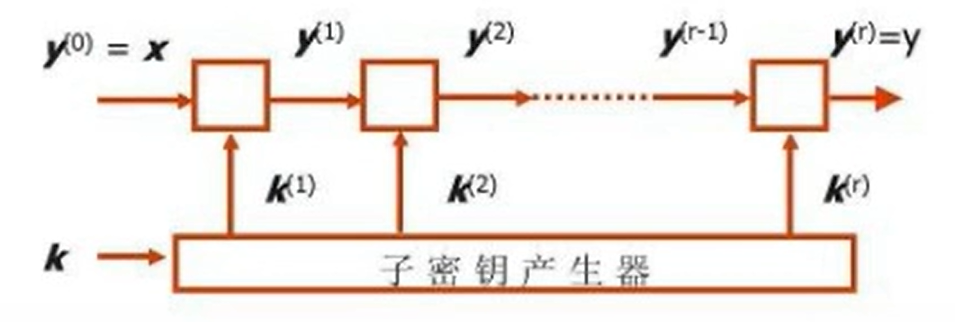
二、分組密碼運行模式

即使有了安全的分組密碼算法，也需要采用適當的工作模式來隱蔽明文的統計特性、數據的格式等，以提高整體的安全性，降低刪除、重放、插入和偽造成功的機會。

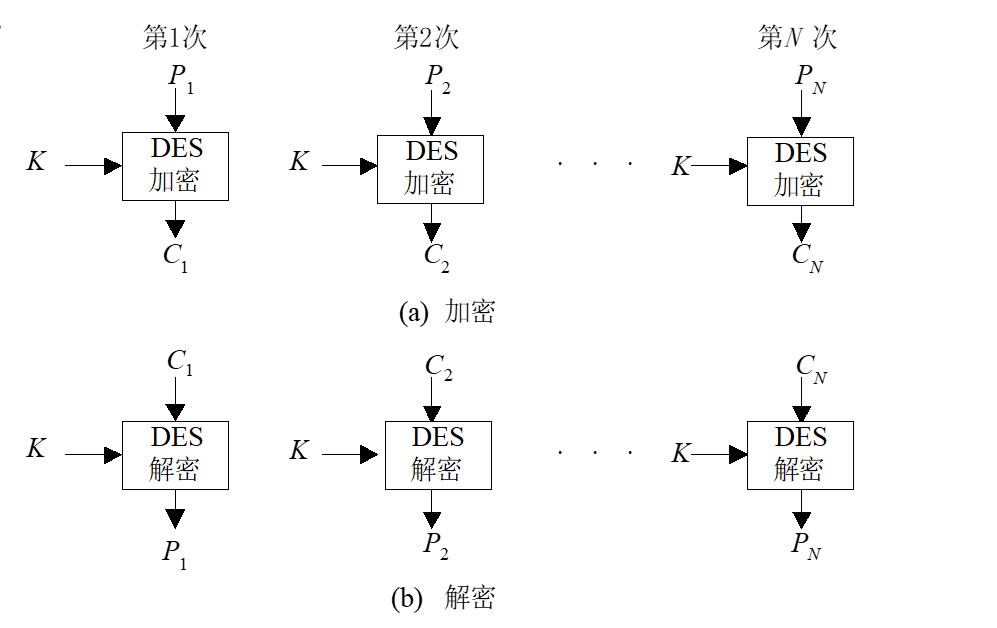
2.1 電碼本模式(ECB)

直接利用加密算法分別對分組數據組加密
在給定的密鑰下同一明文組總產生同樣的密文組。這會暴露明文數據的格式和統計特征。明文數據都有固定的格式，需要以協議的形式定義，重要的數據常常在同一位置上出現，使密碼分析者可以對其進行統計分析、重傳和代換攻擊。

2.2 密碼分組鏈接模式(CBC)

每個明文組 $P_i$ 加密之前，先與反饋至輸入端的前一組密文 $C_{i-1}$ 按位模2求和后，再送至加密算法加密
各密文組 $C_{i}$ 不僅與當前明文組 $P_i$ 有關，而且通過反饋作用還與以前的明文組 $P_1,P_2,...,P_{i-1}$ 有關。

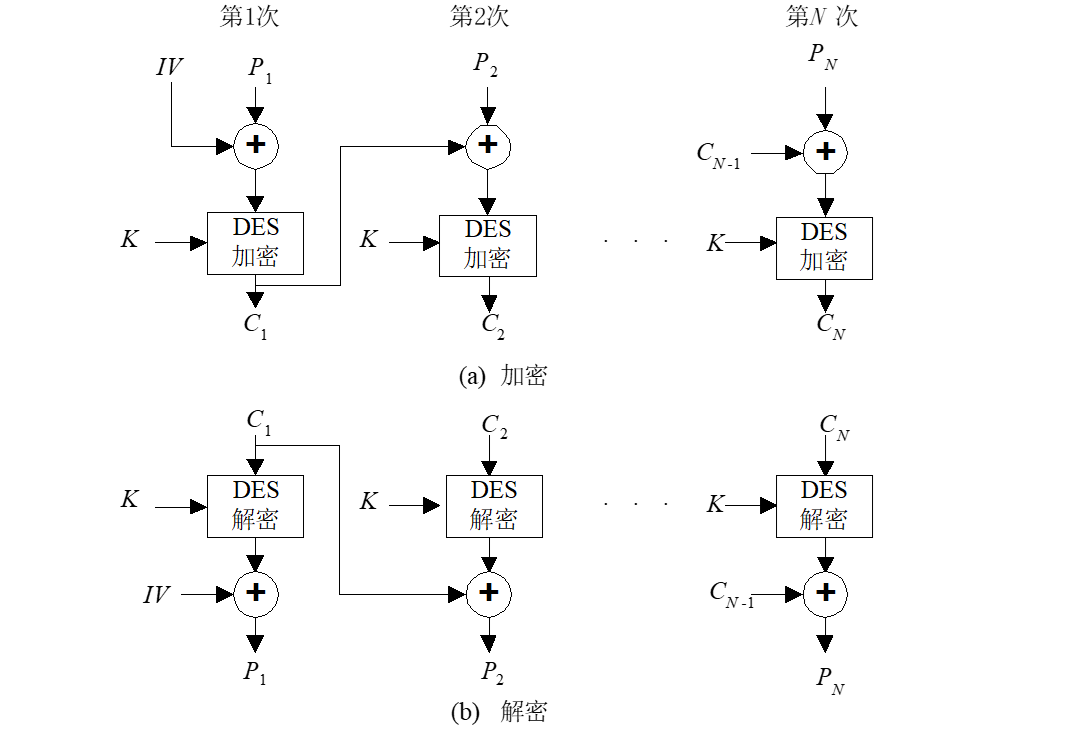
初始矢量IV：第一組明文加密時尚無反饋密文，為此需要在寄存器中預置一個，收發雙方必須選用同一個IV；
實際上，IV的完整性要比其保密性更為重要。在CBC模式下，最好是每發一個消息，都改變IV，比如將其值加1.

CBC的錯誤傳播：

明文有一組中有錯，會使以后的密文組都受影響，但經解密后的恢復結果，除原有誤的一組外，其后各組明文都正確地恢復；
若在傳送過程中，某組密文組 $C_i$ 出錯時，則該組恢復的明文 $P_i'$ 和下一組恢復數據 $P_{i+1}'$ 出錯。再后面的組將不會受 $C_i$ 中錯誤比特的影響

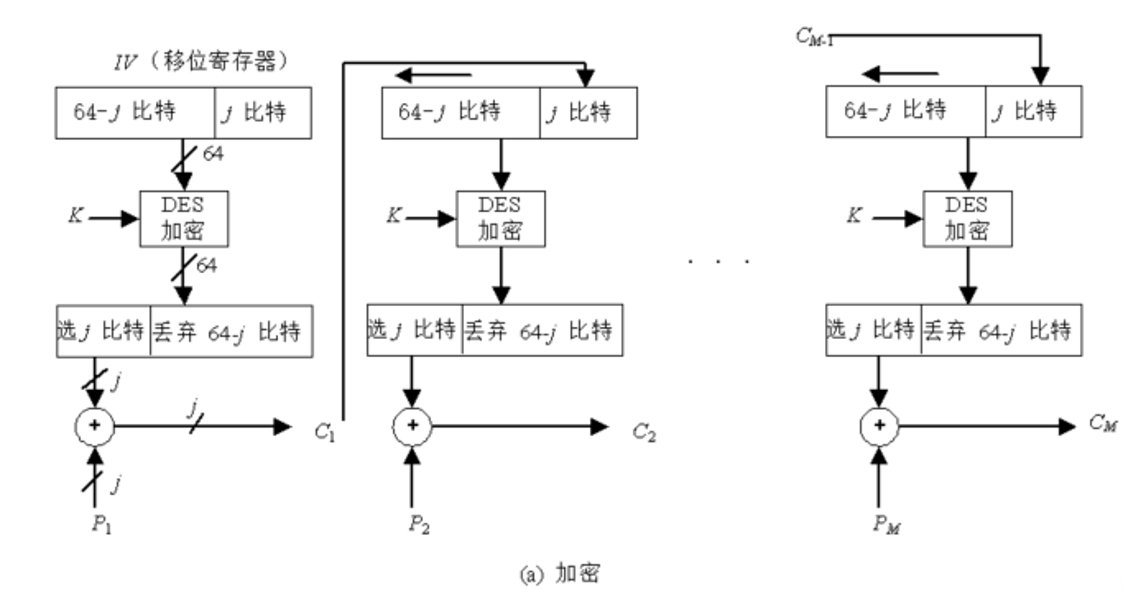
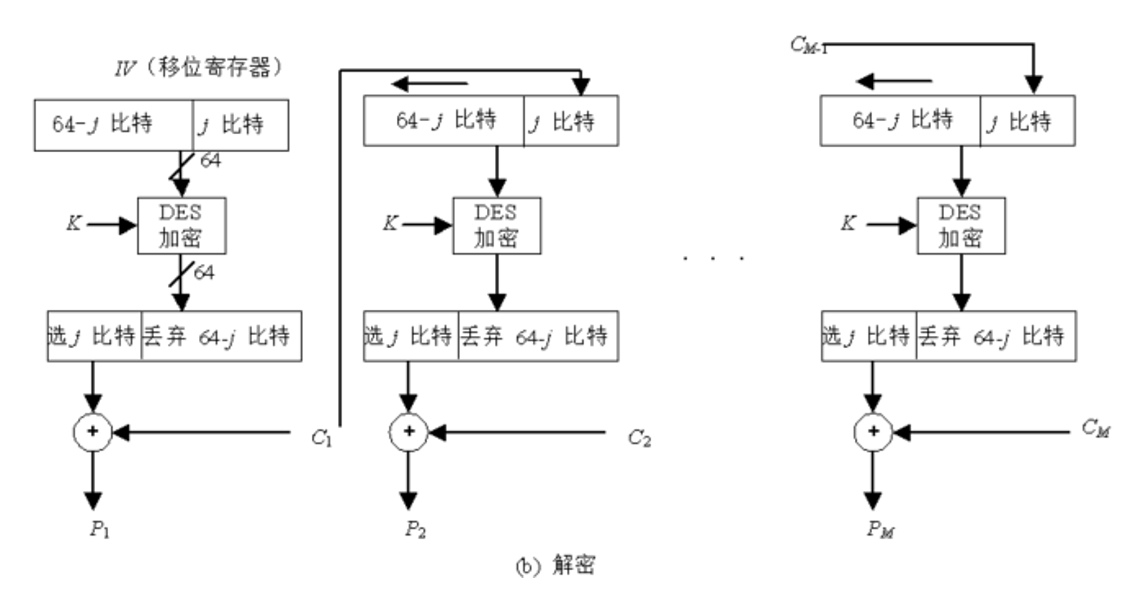
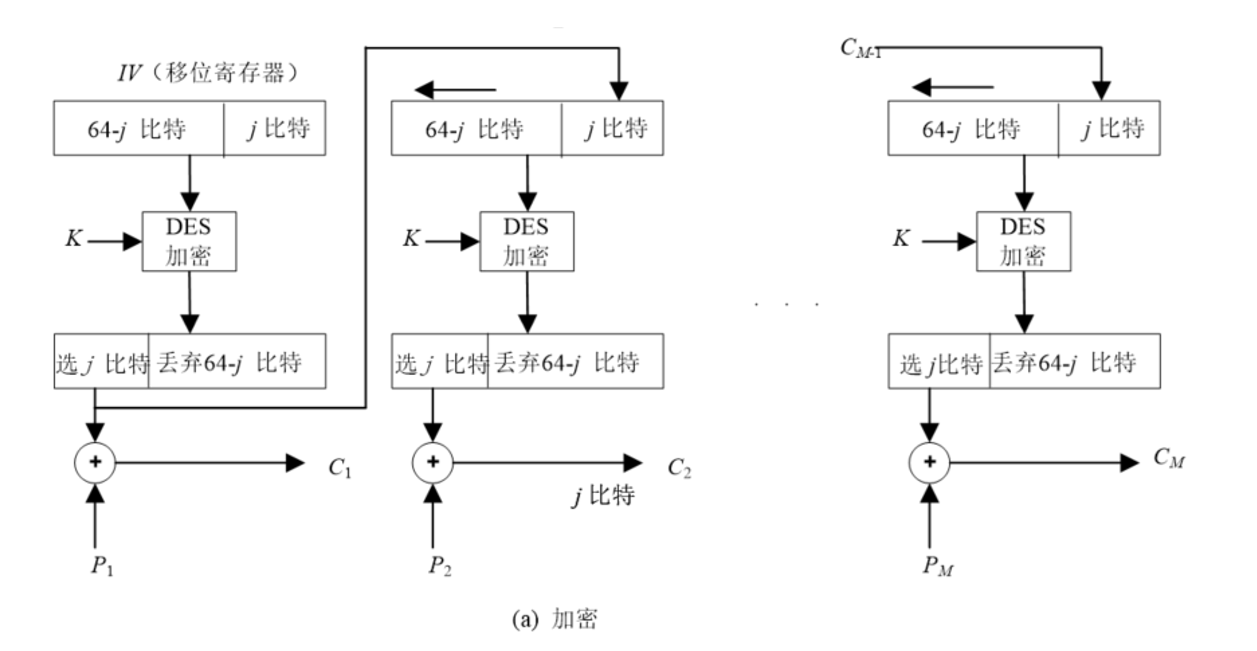
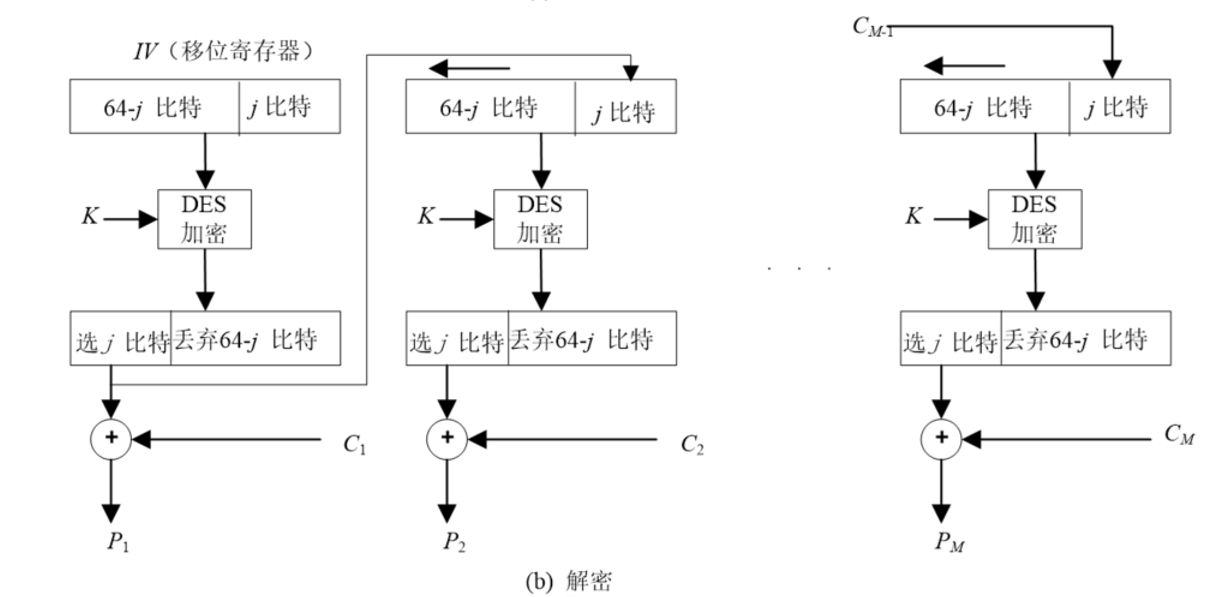
2.3 密碼反饋模式(CFB)

對于k比特密碼反饋模式

若待加密消息必須按字符或按比特處理時，可采用CFB模式
CFB實際上是將加密算法DES作為一個密鑰流產生器，當k=1時就退化為流密碼了

CFB的優點：

特別適合用戶數據格式的需要
能隱蔽明文數據圖樣，也能檢測出對手對于密文的篡改

CFB的缺點：

對信道錯誤較敏感，且會造成錯誤傳播
CFB也需要一個初始矢量，并要和密鑰同時進行更換

2.4 輸出反饋模式(OFB)

將分組密碼算法作為一個密鑰流產生器，其輸出的k比特密鑰直接反饋至分組密碼的輸入端，同時這k比特密鑰和輸入的k比特明文段進行對應位模2相加；
克服了CBC和CFB的錯誤傳播所帶來的問題
對于密文被篡改難以進行檢測

2.5?填充（Padding）

給定加密消息的長度是隨機的，如果按64bit分組時，最后一組消息長度可能不足64bit。此時可以填充一些數字，通常用最后1字節作為填充指示符(PI)。它所表示的十進制數字就是填充占有的字節數。數據尾部、填充字符和填充指示符一起作為一組進行加密。

三、DES算法

雖然DES已有替代的數據加密標準算法，但是它仍是迄今為止得到最廣泛應用的一種算法，也是一種最有代表性的分組加密體制；

分組長度為64 bits;
密文分組長度也是64 bits；
密鑰長度為64 bits，有8 bits奇偶校驗，有效密鑰長度為56 bits；
算法主要包括：初始置換IP、16輪迭代的乘積變換、逆初始置換以及16個子密鑰產生器；

DES算法框圖如下所示：

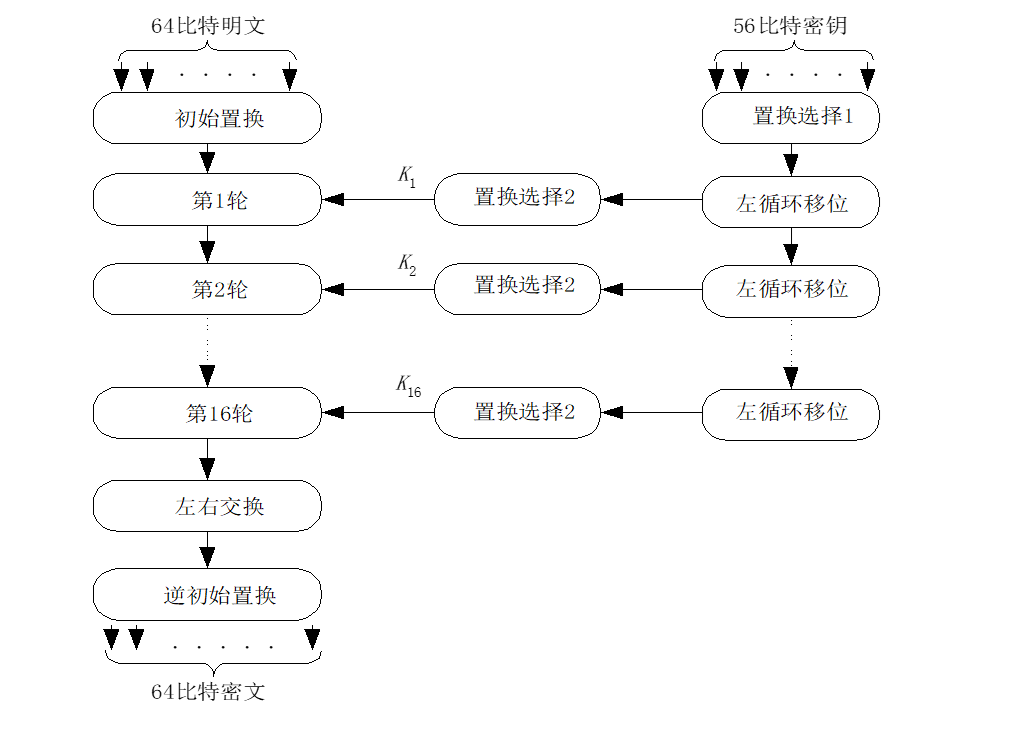
3.1 初始置換IP

將64 bit明文的位置進行置換，得到一個亂序的64 bit明文組，而后分成左右兩段，每段為32 bit

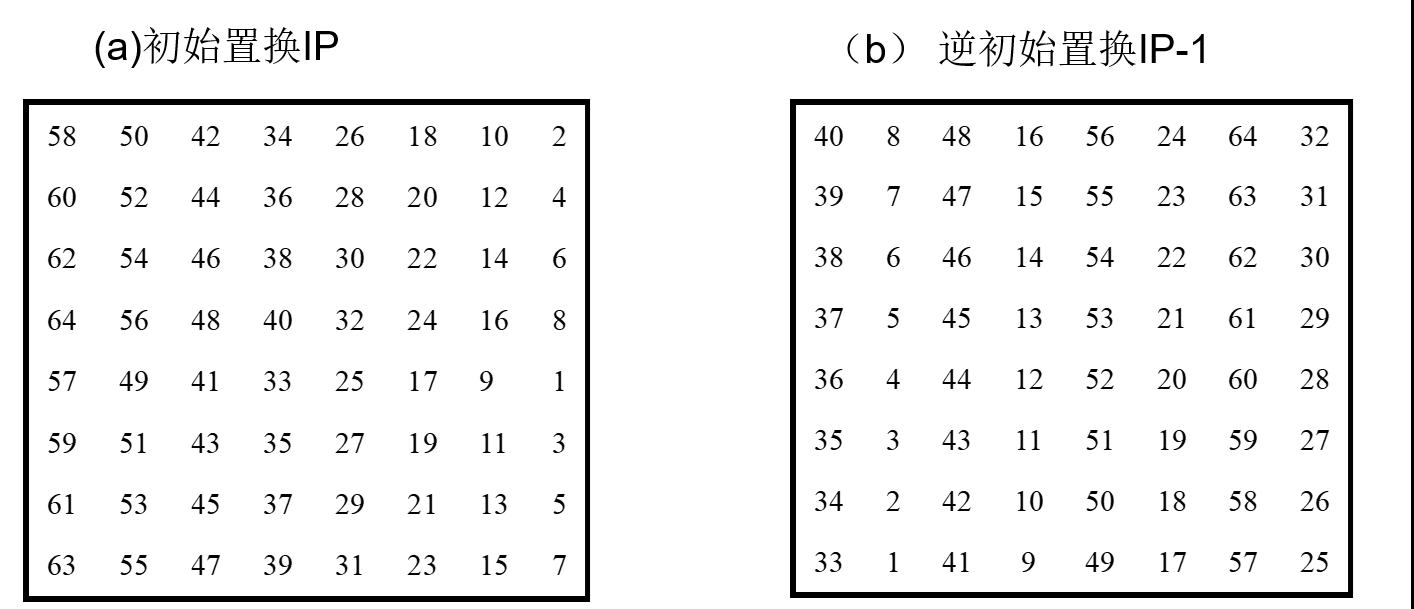
初始置換和逆初始置換在密碼意義上作用不大，它們的作用在于打亂原來輸入 $x$ 的ASCII碼字劃分的關系，并將原來明文的校驗位 $x_8,x_{16},x_{32},x_{64}$ 變成為IP輸出的一個字節

3.2 輪結構

DES算法的核心部分，將經過IP置換后的數據分成32 bit的左右兩組，在迭代過程中彼此左右交換位置
每次迭代時只對右邊的32 bit進行一系列的加密變換，在此輪迭代即將結束時，把左邊的32 bit與右邊得到的32 bit逐位模2相加，作為下一輪迭代時右邊的段，并將原來右邊未經過變換的段直接送到左邊的寄存器中作為下一輪迭代時左邊的段
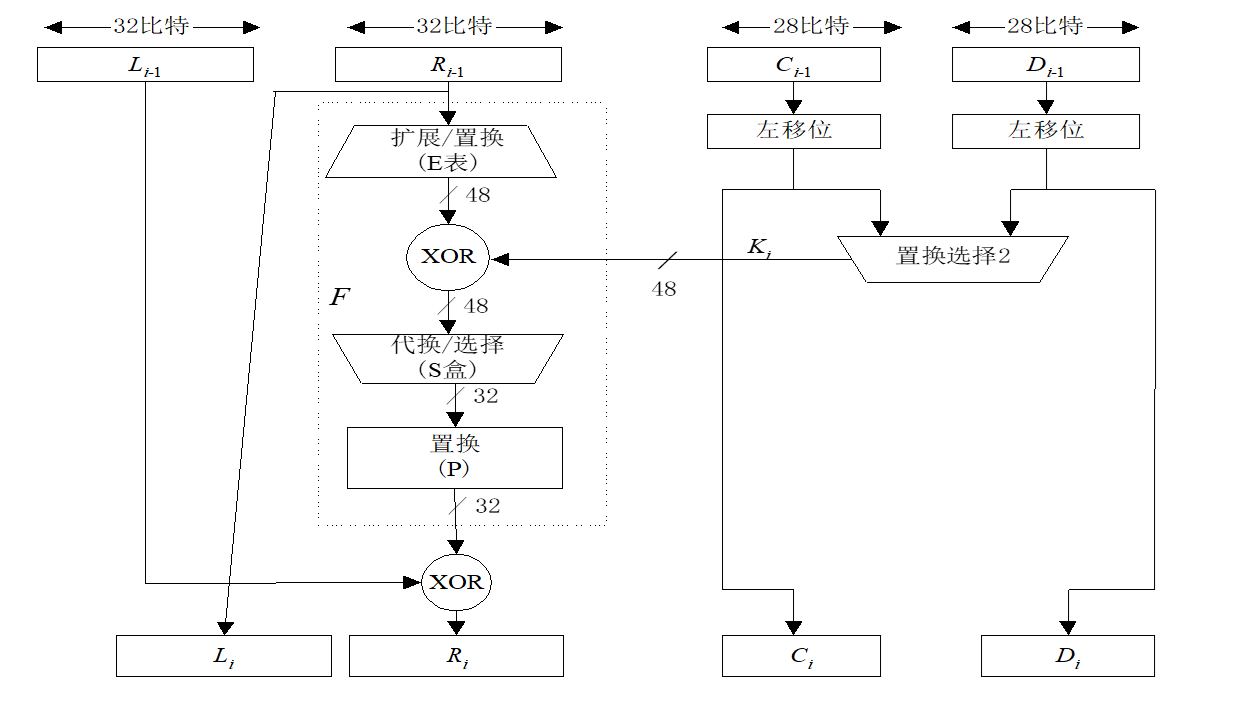
在每一輪迭代時，右邊的段要經過選擇拓展運算E、密鑰加密運算、選擇壓縮運算S、置換運算P和左右混合運算

DES加密算法的輪結構：

3.3 DES的安全性

互補性：若明文組 $x$ 逐位取補，密鑰 $k$ 逐位取補，即 $y=DES_k(x)$ ，則有 $\bar{y}=DES_k(\bar{x}))$ 。這種互補性會使DES在選擇明文破譯下所需的工作量減半;
弱密鑰和半弱密鑰：DES算法在每次迭代時都有一個子密鑰供加密用。如果給定初始密鑰 $k$ ，各輪的子密鑰都相同，即有 $k_1=k_2=...=k_{16}$ 就稱給定密鑰為弱密鑰;

若 $k$ 為弱密鑰，則有 $DES_k(DES_k(x))=x$ ， $DES_k^{-1}(DES_k^{-1}(x))=x$

即以 $k$ 對 $x$ 加密兩次或解密兩次都可恢復出明文。其加密運算和解密運算沒有區別。弱密鑰下使DES在選擇明文攻擊下的搜索量減半。

如果隨機地選擇密鑰，弱密鑰所占比例極小，而且稍加注意就不難避開。因此，弱密鑰的存在不會危及DES的安全性。

DES密鑰太短：窮搜索對DES構成威脅

3.4 兩重DES

用DES進行兩次加密，不能意味著兩重DES加密強度等價于112 bit密鑰的密碼的強度

中途相遇攻擊法

由Diffie和Hellman最早提出，可以降低搜索量。其基本思想如下：

若有明文密文對 $(x_i,y_i)$ 滿足 $y_i=E_{k_2}[E_{k_1}(x_i)]$ 則可得 $z=E_{k_1}(x_i)=D_{k_2}(y_i)$

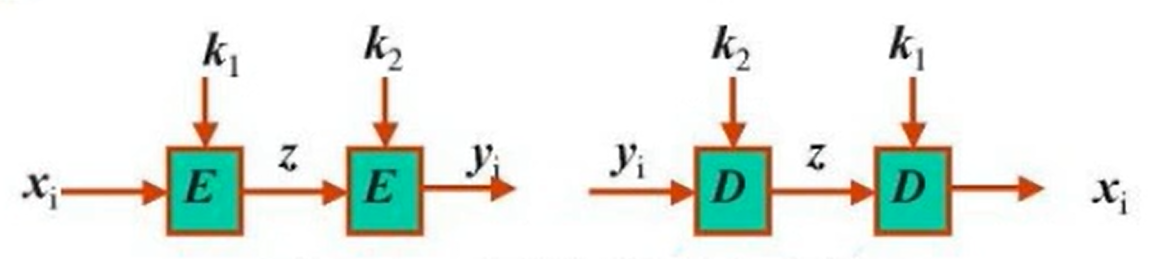
給定一已知明密文對 $(x_1,y_1)$ ，可按下述方法攻擊:

以密鑰 $k_1$ 的所有 $2^{56}$ 個可能的取值對此明文 $x_1$ 加密，并將密文 $z$ 存儲在一個表中;
從所有可能的 $2^{56}$ 個密鑰 $k_2$ 中依任意次序選出一個對給定的密文 $y_1$ 解密，并將每次解密結果 $z$ 在上述表中查找相匹配的值。一旦找到，則可確定出兩個密鑰 $k_1$ 和 $k_2$ ；
以此對密鑰 $k_1$ 和 $k_2$ 對另一已知明密文對 $(x_2,y_2)$ 中的明文 $x_2$ 進行加密，如果能得出相應的密文 $y_2$ 就可確定 $k_1$ 和 $k_2$ 是所要找的密鑰

分析知道：

對于給定明文 $x$ ，以兩重DES加密將有 $2^{64}$ 個可能的密文
可能的密鑰數為 $2^{112}$ 。所以，在給定明文下，將有 $2^{112}/2^{64}=2^{48}$ 個密鑰能產生給定的密文
用另一對64 bits明文密文對進行檢驗，就使虛報率降為 $2^{48-64}=2^{-16}$
這一攻擊法所需要的存儲量為 $2^{56}\times 8$ ?字節，最大試驗的加密次數 $2\times2^{56}$ 。這說明破譯雙重DES的難度為 $2^{57}$ 量級；

3.5 三重DES加密

加密： $y=E_{k_1}[D_{k_2}[E_{k_1}(x)]]$
解密： $x=D_{k_1}[E_{k_2}[D_{k_1}(y)]]$

破譯它的窮舉密鑰搜索量為 $2^{112}\approx 5\times 10^{35}$ 量級，而用差分分析破譯也要超過 $10^{52}$ 量級。此方案仍有足夠的安全性；

四、分組密碼的分析

4.1 差分密碼分析

差分密碼分析是一種攻擊迭代分組密碼的選擇明文統計分析破譯法；
它不是直接分析密文或密鑰的統計相關性，而是分析明文差分和密文差分之間的統計相關性;
給定一個 $r$ 輪迭代密碼，對已知 $n$ 長明文對 $X$ 和 $X'$ ，定義其差分為： $\Delta X=X\bigotimes (X')^{-1}$ 。其中， $\bigotimes$ 表示n bits組 $X$ 的集合中定義的群運算， $(X')^{-1}$ 為 $X'$ 在群中的逆元。
在密鑰作用下，各輪迭代所產生的中間密文差分為 $\Delta Y(i)=Y(i)\bigotimes Y'(i)^{-1},0\leq i\leq r$
$i=0$ 時， $Y(0)=X,Y'(0)=X',\Delta Y(0)=\Delta X$
$i=r$ 時， $\Delta Y=\Delta Y(r)$ , $k^{(i)}$ 是第 $i$ 輪加密的子密鑰， $Y(i)=f(Y(i-1),k^{(i)})$
由于 $X\neq X'$ ,因此， $\Delta Y(i)\neq e$ (單位元)
每輪迭代所用子密鑰 $k^{(i)}$ 與明文統計獨立，且可認為服從均勻分布；

如圖所示為 $r$ 輪迭代分組密碼的差分序列：

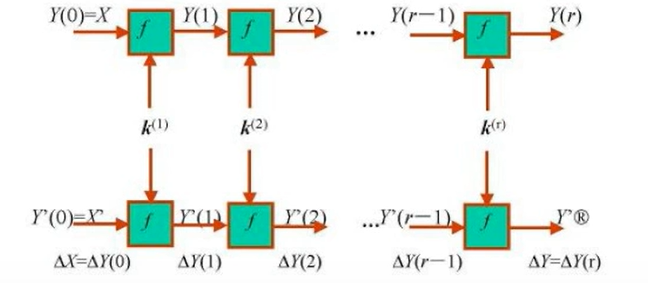
Lai等引入Markov鏈描述多輪迭代分組密碼的差分序列。并定義了Markov密碼
Lai等證明，Markov密碼的差分序列 $\Delta X= \Delta Y(0), \Delta Y(1),..., \Delta Y(r)$ 是一齊次Markov鏈，且若 $\Delta X$ 在群的非零元素上均勻分布，則此Markov鏈是平穩的；
不少迭代分組密碼可歸結為Markov密碼；
一個Markov型密碼，可以用轉移概率 $P(\Delta Y(1)=\alpha _j | \Delta X=\alpha _i)$ 的所有可能轉移值構成的矩陣描述，稱其為齊次Markov鏈的轉移概率矩陣，以 $\Omega$ 表示；
一個n bits分組密碼有 $1\geq i,j\leq M=2^n-1$ 。對所有 $r$ ，有 $\Omega^{r}=P_{ij}^{(r)}=P(\Delta Y(r)=\alpha_j |\Delta X=\alpha_i )$ , $\Omega$ 的每一行都是一概率分布，行元素之和為1；
對于Markov型密碼，當 $\Delta X$ 在非零元素上為均勻分布，則 $\Delta Y$ 為一平穩Markov鏈，此時對于每個 $j$ 有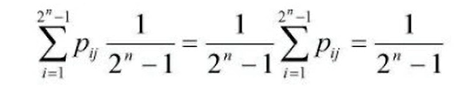即各列元素之和也為1，從而可1知各列也構成一概率分布；
差分密碼分析揭示出，迭代密碼中的一個輪迭代函數 $f$ ，若已知三元組 $\left \{ \Delta Y(i-1),Y(i),Y'(i) |Y(i)=f(Y(i-1),k^{(i)}),Y'(i)=f(Y'(i-1),k^{(i)} \right \}$ ,則不難決定該輪密鑰 $k^{(i)}$ ;
因此輪函數 $f$ 的密碼強度不高。如果已知密文對，且有辦法得到上一輪輸入對的差分，則一般可決定出上一輪的子密鑰(或其主要部分)；
在差分密碼分析中，通常選擇一對具有特定差分 $\alpha$ 的明文，它使最后一輪輸入對的差值 $\Delta Y(r-1)$ 為特定值 $\beta$ 的概率很高；