目錄

1.凸包

2.調色問題

3.極性(Extrem)

4.凸組合(Convex Combination)

?5.問題轉化(Strategy)?編輯

6.In-Triangle test

7.To-Left-test

8.極邊（Extream Edges）

---

1.凸包

凸包就是上面藍色皮筋圍出來的范圍

這些釘子可以轉換到坐標軸中，橫縱坐標表示顏色的比例

2.調色問題

上述問題可以進行一個抽象，抽象為一個color space

結論

• 如果有1種顏料可以被2種顏料勾兌出來，它必然位于二者之間的那條連線上
• 如果有1種顏料可以被3種顏料勾兌出來，它必然位于三角形內
• 勾兌比例與距離成反比

3.極性(Extrem)

藍色的為極點

極點上存在一條直線，使得所有的點落在它的一側

4.凸組合(Convex Combination)

為什么最小值必須>=0 ?

因為這種顏色大不了不用，但也不可能是負的

?5.問題轉化(Strategy)

如果是極點那么久不可能在一個三角形的內部，所以采用排除法，剩下的就是極點

6.In-Triangle test

遍歷所有可能的三角線組合，排除非極點

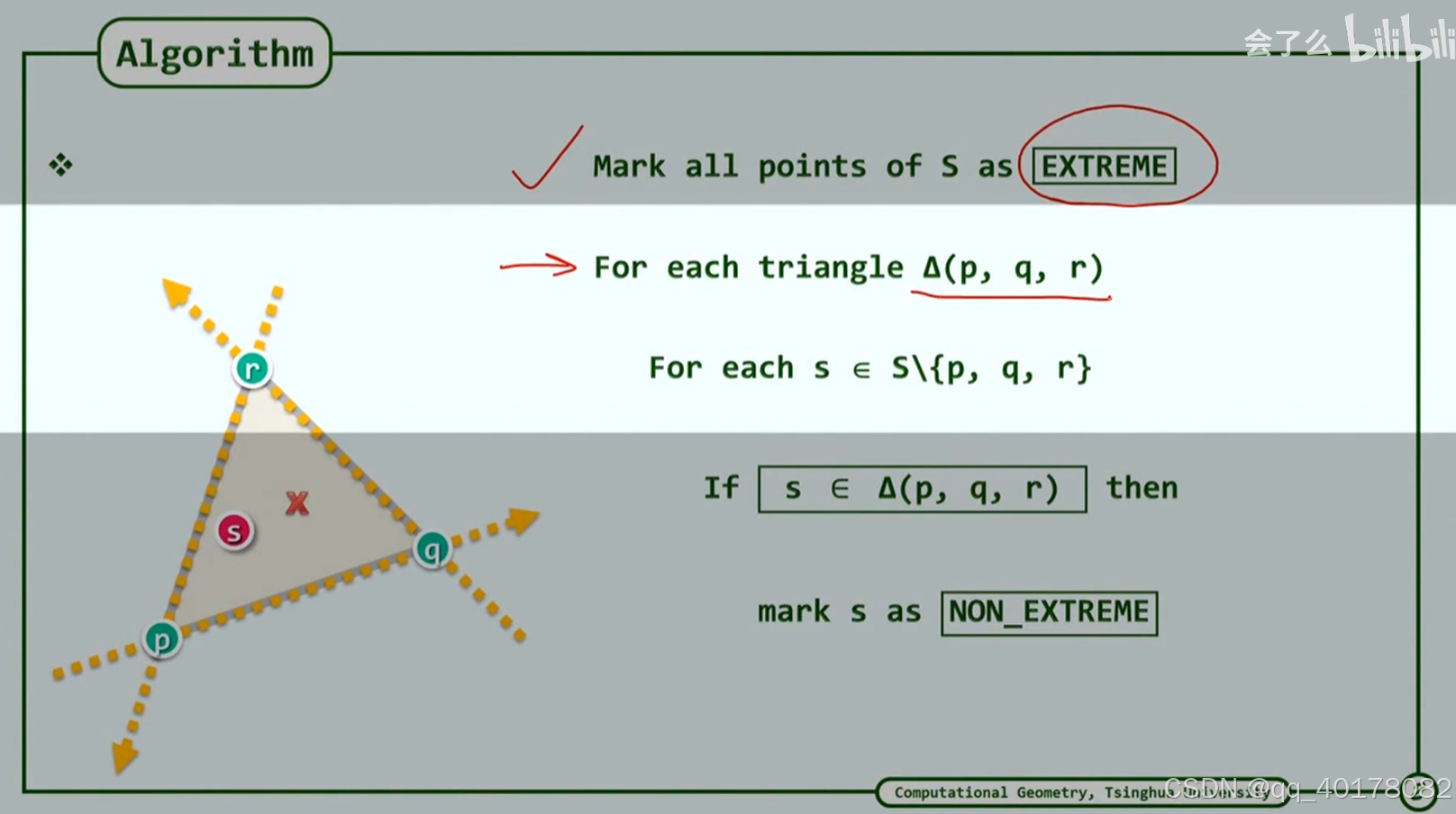
低效做法

更加聰明的做法，如果一個點位于三條直線的left，那么它一定位于三角形內

7.To-Left-test

如何高效的判斷一個點是否是包含在一個三角形的內部是計算幾何里的一個基礎問題。

In Triangle Test問題也可以用來解決計算幾何里的一個基礎問題就是?凸包問題?。

問題描述：

給出一個點s，判斷其是否在一個三角形（p, q, r）內部。

問題求解：

判斷一個點是否在三角形內部等價于對于三條邊分別做To left test的結果一致。

那么現在的問題就是如何高效和精確的實現To left test。

只有s位于pq這條線段左側才會取正。

關于這個可以使用空間坐標系的海倫公式來求解。

? ? ? ? ? ? ??| p.x p.y 1 |

2 * S =? ?| q.x q.y 1 |

? ? ? ? ? ? ? | s.x s.y 1 |

并且這個公式是有向的，當三個點是逆時針排列的時候該行列式的返回結果是正數，當三個點是順時針排列的時候行列式的返回結果是負數。

1 2 3 4 5 6 7 8

bool?to_left_test(int[] p,?int[] q,?int[] s) { ????return?area2(p, q, s) > 0; } int?area2(int[] p1,?int[] p2,?int[] p3) { ????return?p1[0] * p2[1] + p1[1] * p3[0] + p2[0] * p3[1] - ????????p2[1] * p3[0] - p1[1] * p2[0] - p1[0] * p3[1]; }

To left test 幾乎貫穿了整個計算幾何，不僅是計算凸包的核心，也是很多其他計算幾何問題的關鍵算法。

例如：判斷兩條線段是否相交，只需要做4次to left test即可。?

8.極邊（Extream Edges）

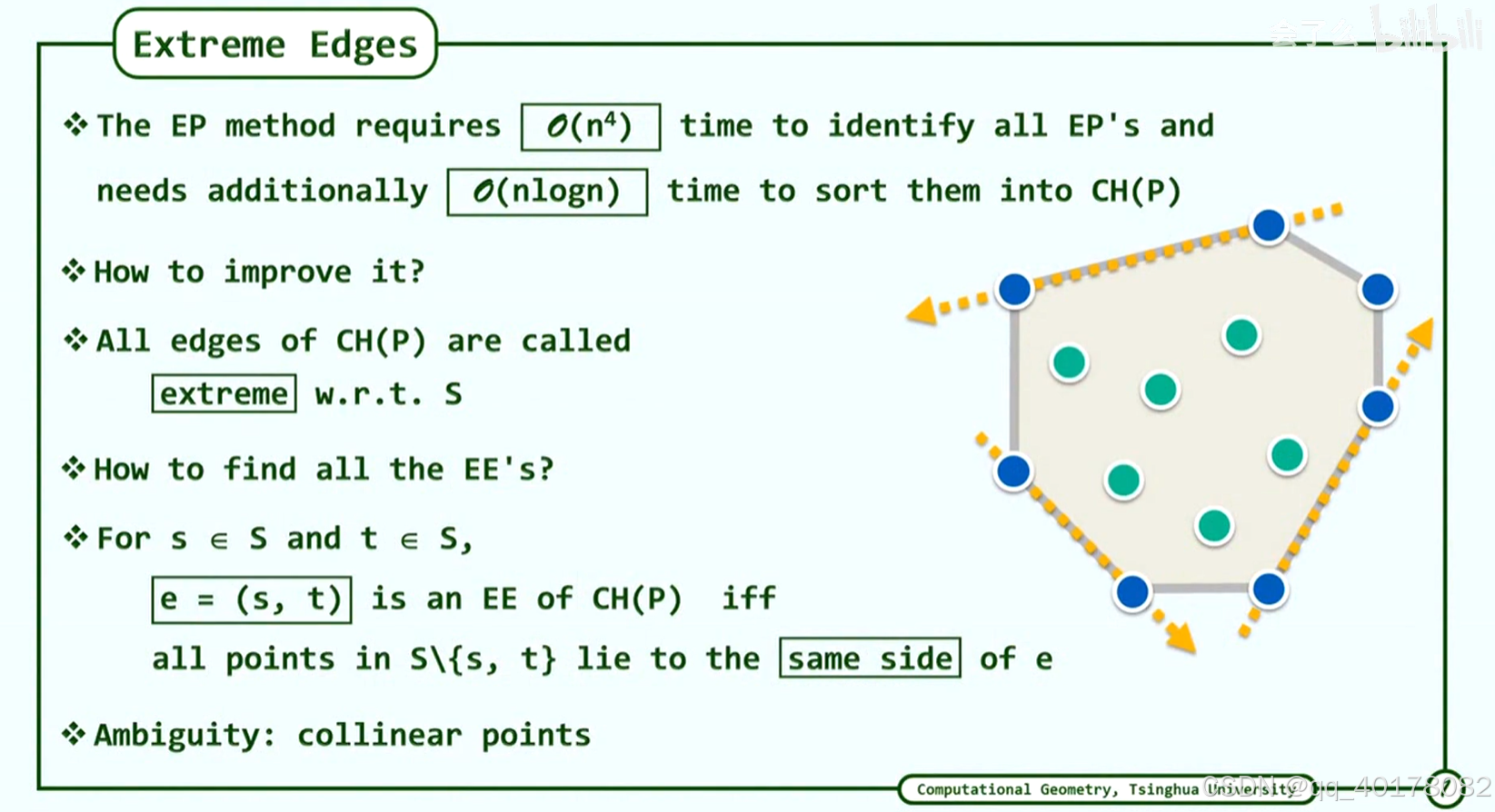
極邊：所有的點落在同一側，就是極邊

算法實現

極邊的算法效率高于極點的算法效率

參考

In Triangle Test / To Left Test - hyserendipity - 博客園