? ?

??????????? 💓 博客主頁：倔強的石頭的CSDN主頁?

???????????📝Gitee主頁：倔強的石頭的gitee主頁

? ? ? ? ? ? ? 文章專欄：《數據結構與算法》

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ????期待您的關注

?

?

?

目錄

一、引言

堆排序的簡介

堆排序的特點

二、堆的概念

三、堆排序算法的原理

四、堆排序的步驟

🍃構建堆?

🍃交換與調整

🍃重復過程

五、堆排序的性能分析

🍃時間復雜度：

🍃空間復雜度：

六、示例代碼

七、總結

---

?

一、引言

堆排序的簡介

堆排序（Heap Sort）是一種基于堆數據結構實現的排序算法。利用堆這種數據結構的高效性，通過構建和調整堆來實現排序，是一種性能優秀的排序算法。

堆排序的特點

1. 時間復雜度：堆排序的最壞、最好、平均時間復雜度均為O(nlogn)，其中n是待排序元素的數量。
2. 穩定性：堆排序在排序過程中相等的元素不會交換位置，因此它是穩定的排序算法。
3. 選擇排序：堆排序是一種選擇排序，它總是選擇當前未排序部分的最大（或最小）元素進行排序。

?

二、堆的概念

關于堆的詳細介紹，參考前置文章

【數據結構與算法】探索數組在堆數據結構中的妙用：從原理到實現-CSDN博客

?

三、堆排序算法的原理

• 堆排序的基本思想是將待排序的序列構建成一個堆，然后依次將堆頂元素與堆尾元素交換，并將堆的大小減小1，再對剩余的堆進行調整，使其滿足堆的性質。
• 重復這個過程，直到堆的大小為1，此時排序完成。?

四、堆排序的步驟

🍃構建堆?

借助建堆算法，降序建小堆，升序建大堆，可以選擇向上或者向下調整算法

向上調整建堆的原理：
模仿堆的插入操作來構建堆，從第一個子結點開始，將它看做是新插入的元素，向上調整至滿足堆的性質，然后依次往后走，直到最后一個葉子節點完成上述調整

向下調整建堆的原理：
從最后一個父結點開始，先保證它和左右子樹成為堆，然后依次往前走，保證每個父結點與左右子樹成堆，直到最后根結點與左右子樹成堆

?

關于建堆的向上調整算法和向下調整算法有時間復雜度推導

限于篇幅，這里就不展開推導了，直接給出結論

• 向下調整建堆的時間復雜度為O（N）
• 向上調整算法的時間復雜度為O（n*logN）

向下調整算法優于向上調整，所以應該選擇向下調整算法

?這里分別給出向下調整建小堆和向下調整建大堆的算法

（如果關于向上調整算法和向下調整算法有疑惑，建議了解完堆的這篇文章之后再來看

【數據結構與算法】探索數組在堆數據結構中的妙用：從原理到實現-CSDN博客）

void Adjustdownsmall(DataType* a, int parent, int size)//向下調整建小堆算法
{int child = parent * 2 + 1;//先假定左孩子小while (child < size)//循環條件是未調整至葉子節點{if (child + 1 < size && a[child + 1] < a[child])//如果右孩子存在且更小，改變為右孩子child++;if (a[child] < a[parent])//如果子節點小于父節點，交換位置{Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}elsebreak;}
}
void Adjustdownbig(DataType* a, int parent, int size)//向下調整建大堆算法
{int child = parent * 2 + 1;//先假定左孩子大while (child < size)//循環條件是未調整至葉子節點{if (child + 1 < size && a[child + 1] > a[child])//如果右孩子存在且更大，改變為右孩子child++;if (a[child] > a[parent])//如果子節點大于父節點，交換位置{Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}elsebreak;}
}

?

🍃交換與調整

建堆之后，就是排序
以降序為例，每次將堆頂與堆尾數據交換（相當于將當前的最小值挪到最后），然后堆尾數據偽刪除（有效數據個數--，不是真刪除）進行一輪向下調整，恢復堆的結構

?

Swap(&a[0], &a[end]);//交換堆頂和堆尾數據
end--;
Adjustdownsmall(a, 0, end);//向下調整恢復堆的結構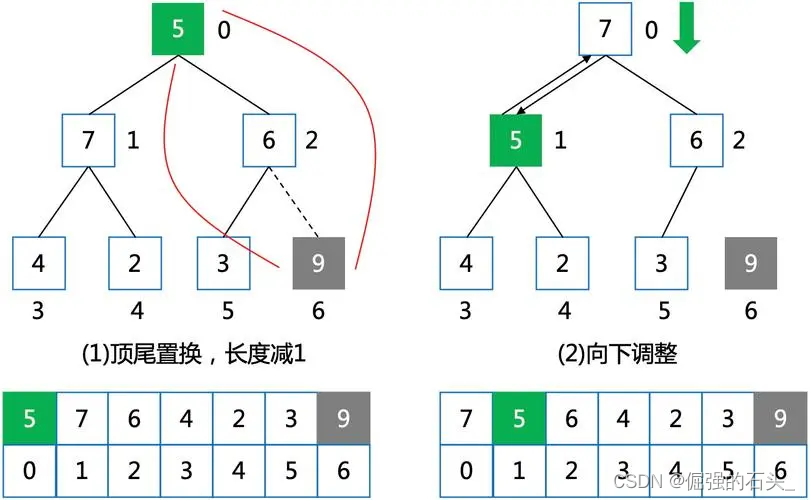

?

?

🍃重復過程

?重復上述交換與調整的過程，直到堆的大小為1，此時排序完成。

?

五、堆排序的性能分析

🍃時間復雜度：

1. 建堆：對于長度為n的數組，建堆的時間復雜度為O(n)。這是因為建堆的過程中，元素需要逐個從數組尾部加入到堆中，并重新調整堆的結構以維持其性質。每個元素加入堆中最多會觸發從該元素到根節點的路徑上元素的重新調整，因此，平均而言，每個元素會觸發O(log n)次調整。所以，建堆的總時間復雜度為O(n *log n)。但是，由于建堆的過程是線性的（從最后一個非葉子節點開始，逐個向上調整），所以實際的時間復雜度為O(n)。
2. 排序：在排序階段，每次從堆頂取出最大（或最小）元素，并重新調整堆結構的時間復雜度為O(log n)。因為需要排序n個元素，所以排序階段的時間復雜度為O(n *log n)。

綜上，堆排序的總時間復雜度為O(n) + O(n *log n) = O(n *log n)。

?

🍃空間復雜度：

堆排序的空間復雜度為O(1)。這是因為堆排序是原地排序算法，它只需要常數個額外的空間來存儲臨時變量，而不需要額外的存儲空間來存儲待排序的數組。所有的操作都是直接在原數組上進行的。所以，堆排序的空間復雜度非常低。

六、示例代碼

（分別給出了完整的降序排序算法和升序排序算法）

#include<stdio.h>
#include<stdlib.h>#if 1
//堆排序
typedef int DataType;
void Swap(DataType* a, DataType* b)
{DataType tmp = *a;*a = *b;*b = tmp;
}
void Adjustdownsmall(DataType* a, int parent, int size)//向下調整建小堆算法
{int child = parent * 2 + 1;//先假定左孩子小while (child < size)//循環條件是未調整至葉子節點{if (child + 1 < size && a[child + 1] < a[child])//如果右孩子存在且更小，改變為右孩子child++;if (a[child] < a[parent])//如果子節點小于父節點，交換位置{Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}elsebreak;}
}
void Adjustdownbig(DataType* a, int parent, int size)//向下調整建大堆算法
{int child = parent * 2 + 1;//先假定左孩子大while (child < size)//循環條件是未調整至葉子節點{if (child + 1 < size && a[child + 1] > a[child])//如果右孩子存在且更大，改變為右孩子child++;if (a[child] > a[parent])//如果子節點大于父節點，交換位置{Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}elsebreak;}
}void HeapSortDOrder(DataType* a,int size)//降序排序
{//向下調整建小堆for (int i = (size - 2) / 2; i >= 0; i--)//從最后一個父節點調整{Adjustdownsmall(a, i, size);}int end = size - 1;while (end>0){Swap(&a[0], &a[end]);//交換堆頂和堆尾數據end--;Adjustdownsmall(a, 0, end);//向下調整恢復堆的結構}
}
void HeapSortAOrder(DataType* a, int size)//升序排序
{//向下調整建大堆for (int i = (size - 2) / 2; i >= 0; i--)//從最后一個父節點調整{Adjustdownbig(a, i, size);}int end = size - 1;while (end > 0){Swap(&a[0], &a[end]);//交換堆頂和堆尾數據end--;Adjustdownbig(a, 0, end);//向下調整恢復堆的結構}
}
#endifvoid print(DataType* a, int size)
{for (int i = 0; i < size; i++){printf("%d ", a[i]);}printf("\n");
}
int main()
{int arr[] = { 12,3,5,78,46,15,23,19,20,36,52 };int size = sizeof(arr) / sizeof(arr[0]);HeapSortDOrder(arr, size);//降序print(arr, size);HeapSortAOrder(arr, size);//升序print(arr, size);}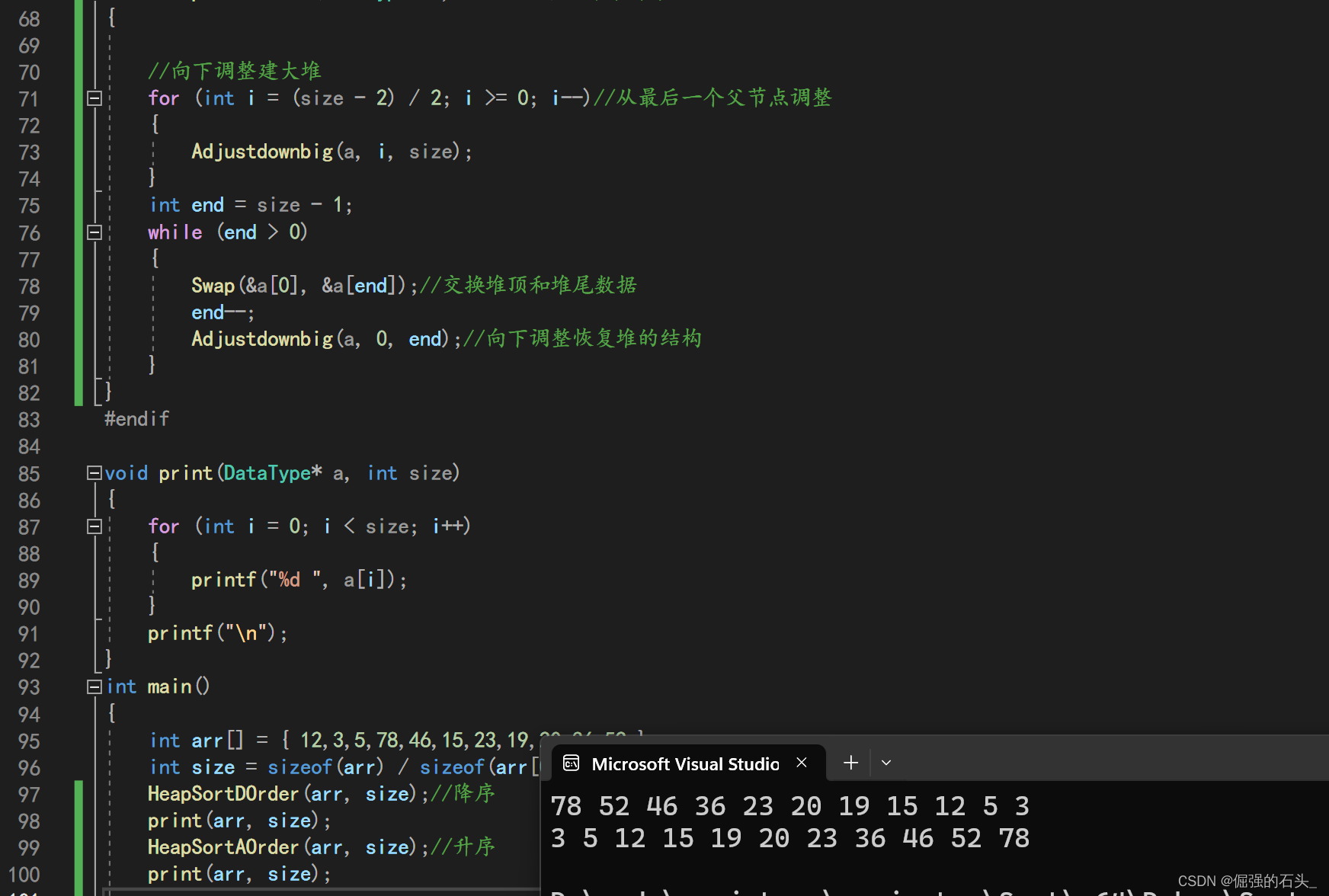

?

七、總結

堆排序算法是一種高效且實用的排序算法，它通過利用堆數據結構的特點和性質，實現了對數據的高效排序。在實際應用中，我們可以根據問題的特點選擇使用堆排序算法，以提高程序的性能和效率。

?