排序算法(1)之插入排序----直接插入排序和希爾排序

?個人主頁：C++忠實粉絲
歡迎點贊👍 收藏? 留言? 加關注💓本文由 C++忠實粉絲?原創

排序之插入排序----直接插入排序和希爾排序(1)

收錄于專欄【數據結構初階】
本專欄旨在分享學習數據結構學習的一點學習筆記，歡迎大家在評論區交流討論💌

1.排序的概念及其運用

1.1排序的概念

1.2排序運用?

1.2.1?購物和電商

1.2.2?圖書館和書店

1.2.3?教育

1.2.4?交通和物流

1.2.5?餐飲業

1.3 常見的排序算法?

2.插入排序

2.1基本思想

2.2直接插入排序

2.2.1直接插入排序的概念:

2.2.2直接插入排序示例:

2.2.3動圖演示:

?2.2.4代碼實現:

2.2.5測試代碼:

2.2.6時間復雜度分析

2.3希爾排序?( 縮小增量排序 )

2.3.1希爾排序的概念

2.3.2希爾排序圖解分析:

2.3.3代碼展示:

?2.3.4測試代碼:

2.3.5希爾排序時間復雜分析:

2.3.6 希爾排序的特性總結：

2.4希爾排序與直接插入排序的關系和比較?

3總結?

1.排序的概念及其運用

1.1排序的概念

排序：所謂排序，就是使一串記錄，按照其中的某個或某些關鍵字的大小，遞增或遞減的排列起來的操作。

穩定性：假定在待排序的記錄序列中，存在多個具有相同的關鍵字的記錄，若經過排序，這些記錄的相對次序保持不變，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，則稱這種排序算法是穩定的；否則稱為不穩定的。

內部排序：數據元素全部放在內存中的排序。

外部排序：數據元素太多不能同時放在內存中，根據排序過程的要求不斷地在內外存之間移動數據的排序。

1.2排序運用?

排序算法在生活中有著廣泛的應用，無論是日常活動還是專業領域，都能看到排序算法的身影。以下是一些具體的例子：

1.2.1?購物和電商

產品排列：在線購物平臺會根據價格、銷量、評價等對商品進行排序，方便用戶查找和比較。
推薦系統：根據用戶的瀏覽和購買歷史，推薦系統會對可能感興趣的商品進行排序。

1.2.2?圖書館和書店

分類與索引：圖書按字母順序、類別、作者或者出版日期排序，方便讀者查找。
借閱記錄：按時間順序記錄借還書信息，便于管理和統計。

1.2.3?教育

成績排名：考試成績會按照分數排序，以便評估學生的表現。
學籍管理：按學號或姓名排序學生信息，便于查詢和管理。

1.2.4?交通和物流

航班和列車時刻表：按出發時間、目的地等排序，方便乘客查詢和安排行程。
快遞分揀：按目的地、優先級等對包裹進行排序，提高運送效率。

1.2.5?餐飲業

菜單排序：餐廳菜單按菜品類型、受歡迎程度等排序，方便顧客選擇。
訂單處理：按下單時間、優先級等排序訂單，確保及時準確地完成服務。

這些例子展示了排序算法在各種場景中的重要性和廣泛應用，從而提高了效率和用戶體驗。無論是簡單的字母排序還是復雜的多條件排序，排序算法在現代生活中都是不可或缺的工具。

1.3 常見的排序算法?

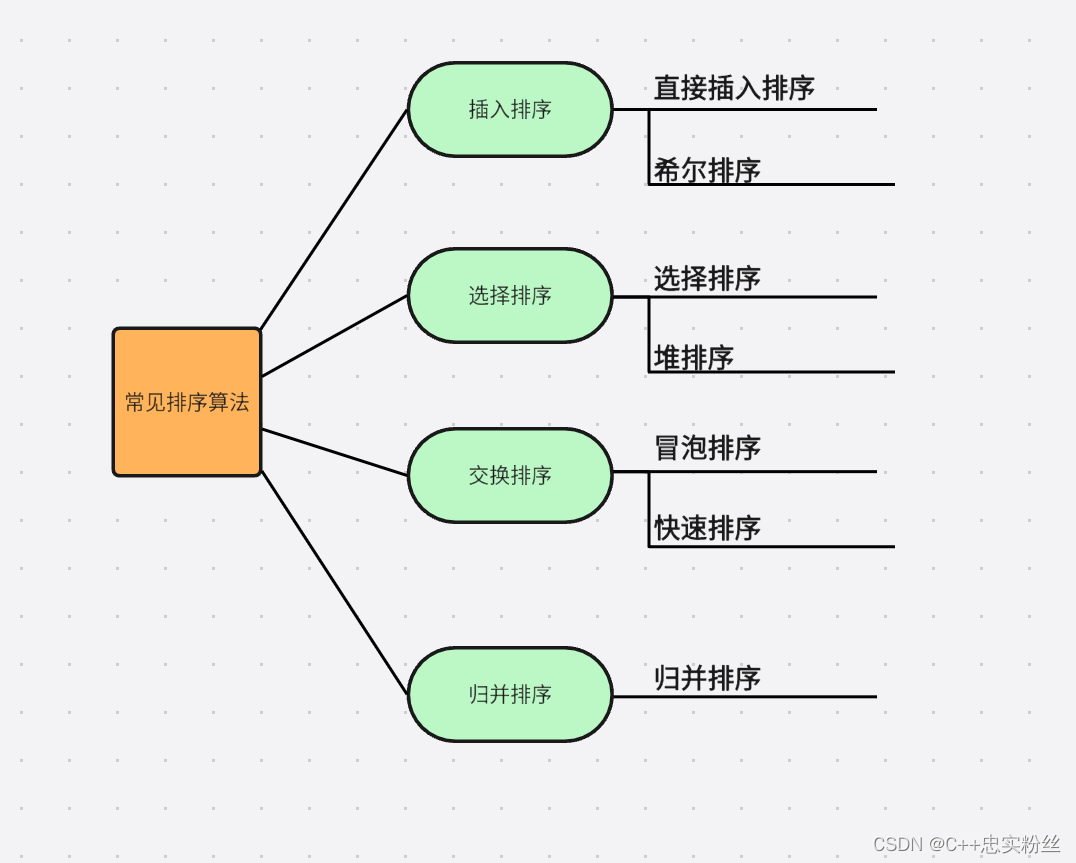
大家可以去下面鏈接查看各個排序算法的動態演示效果

--Comparison Sorting Visualization (usfca.edu)?

2.插入排序

2.1基本思想

直接插入排序是一種簡單的插入排序法，其基本思想是： 把待排序的記錄按其關鍵碼值的大小逐個插入到一個已經排好序的有序序列中，直到所有的記錄插入完為止，得到一個新的有序序列。

實際中我們玩撲克牌時，就用了插入排序的思想

2.2直接插入排序

2.2.1直接插入排序的概念:

直接插入排序（Insertion Sort）是一種簡單直觀的排序算法，其基本思想是逐步構建有序序列。具體操作如下：

初始狀態：將序列分為兩部分，一部分是有序序列，初始時只包含第一個元素；另一部分是無序序列，包含剩余的元素。

排序過程：

從第二個元素開始，依次將該元素插入到前面已經排好序的序列中的合適位置。
假設當前要插入的元素為?current_value，將?current_value?與已排序序列中的元素從后向前逐個比較。
如果發現已排序元素比?current_value?大，則將該元素后移一位，直到找到比?current_value?小的位置，或者到達序列的開頭。
將?current_value?插入到找到的位置后，此時已排序序列長度增加一。

重復：重復以上步驟，直到所有元素都插入到有序序列中。

結束：當所有元素都插入到有序序列后，排序完成。

2.2.2直接插入排序示例:

假設要對數組 [5, 2, 4, 6, 1, 3] 進行直接插入排序：

初始時，有序序列為?[5]，無序序列為?[2, 4, 6, 1, 3]。
將?2?插入到?[5]?中，得到?[2, 5]，無序序列變為?[4, 6, 1, 3]。
將?4?插入到?[2, 5]?中，得到?[2, 4, 5]，無序序列變為?[6, 1, 3]。
依此類推，直到所有元素都插入到有序序列中，最終得到排序后的數組?[1, 2, 3, 4, 5, 6]。

直接插入排序雖然簡單，但在某些特定情況下仍然可以提供不錯的性能，特別是在處理部分有序的數據或者數據量較小時。

2.2.3動圖演示:

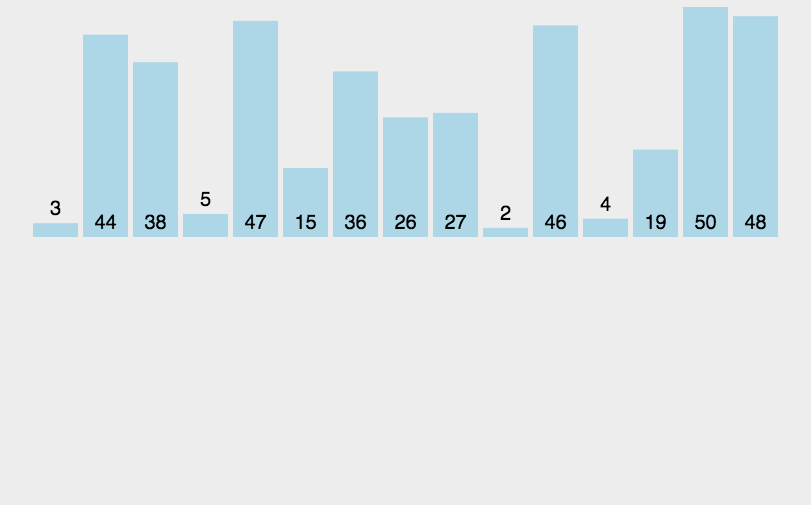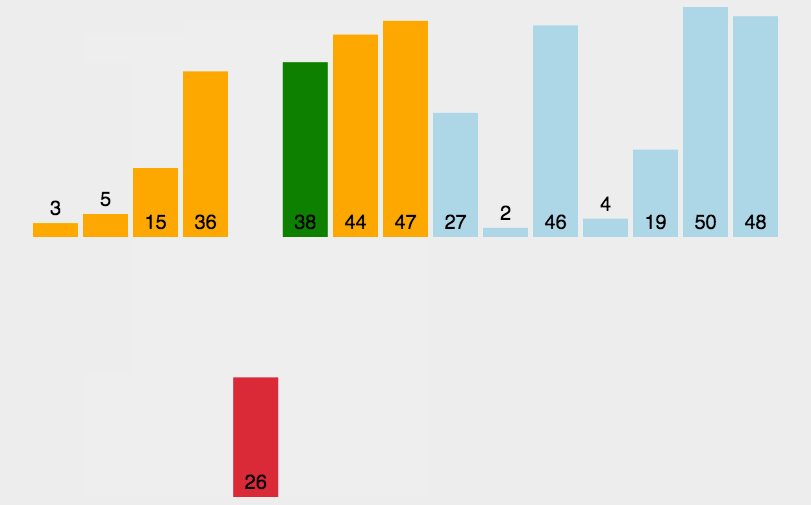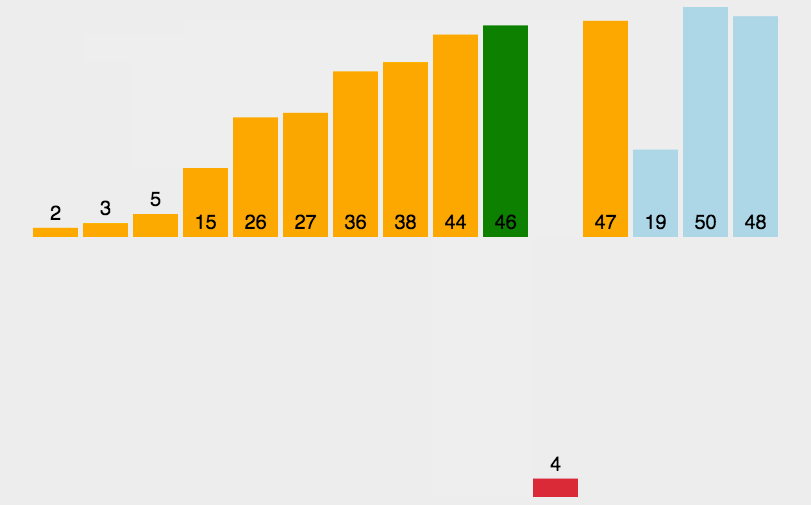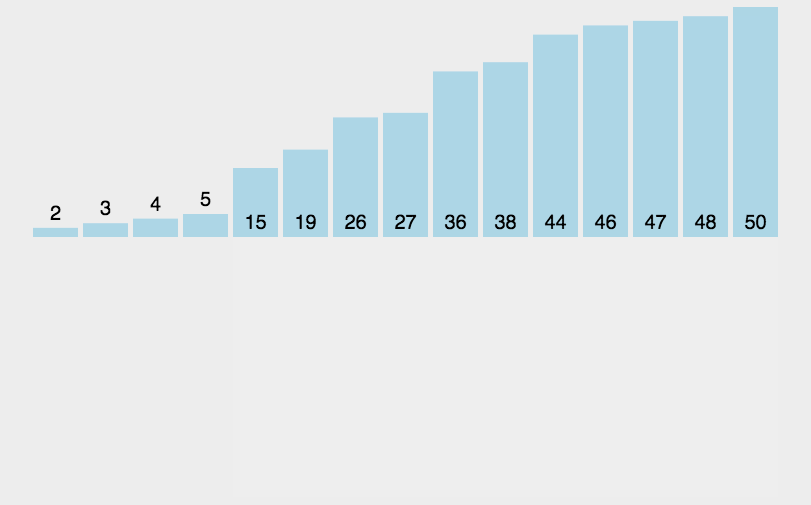
?2.2.4代碼實現:

void InsertSort(int* a, int n)
{//  [0, n-1]for (int i = 0; i < n - 1; i++){// [0, n-2]是最后一組// [0,end]有序 end+1位置的值插入[0,end]，保持有序int end = i;int tmp = a[end + 1];while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];--end;}else{break;}}a[end + 1] = tmp;}
}

分析:

外層循環（i 循環）：

for (int i = 0; i < n - 1; i++)?循環遍歷數組，從第一個元素到倒數第二個元素。每次迭代開始時，數組從?a[0]?到?a[i]?是已經排好序的部分。

內層循環（end 循環）：

int end = i;?將當前元素?a[i+1]?視為待插入的元素。
int tmp = a[end + 1];?記錄待插入元素的值。

插入過程：

while (end >= 0)?內層循環用于找到待插入元素?tmp?的正確位置。
if (tmp < a[end])?如果待插入元素比當前位置?a[end]?的元素小，則將?a[end]?向后移動一位，即?a[end + 1] = a[end];，同時?end--?繼續向前比較。
當找到合適的位置（即?tmp >= a[end]），退出內層循環。

插入操作：

a[end + 1] = tmp;?將?tmp?插入到找到的合適位置?end + 1?處，此時數組從?a[0]?到?a[i+1]?又變成有序狀態。

?注意:我們的外層循環for (int i = 0; i < n - 1; i++)?是遍歷的是我們已經排好序的數組,我們需要排的數為a[end+1],也就是a[i+1],所以這里i<n-1,不能等于n-1

2.2.5測試代碼:

測試鏈接:912. 排序數組 - 力扣（LeetCode）

題目描述:

給你一個整數數組?nums，請你將該數組升序排列。

示例 1：

輸入：nums = [5,2,3,1]
輸出：[1,2,3,5]

示例 2：

輸入：nums = [5,1,1,2,0,0]
輸出：[0,0,1,1,2,5]

提示：

1 <= nums.length <= 5 * 104
-5 * 104 <= nums[i] <= 5 * 104

代碼展示:

void InsertSort(int* a, int n)
{for(int i = 0; i < n-1; i++){int end = i;int tmp = a[end + 1];while(end >= 0){if(a[end] > tmp){a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = tmp;}
}int* sortArray(int* nums, int numsSize, int* returnSize) {(*returnSize) = numsSize;int* array = (int*)malloc(sizeof(int)*(*returnSize));for(int i = 0; i < numsSize; i++){array[i] = nums[i];}InsertSort(array, numsSize);return array;
}

2.2.6時間復雜度分析

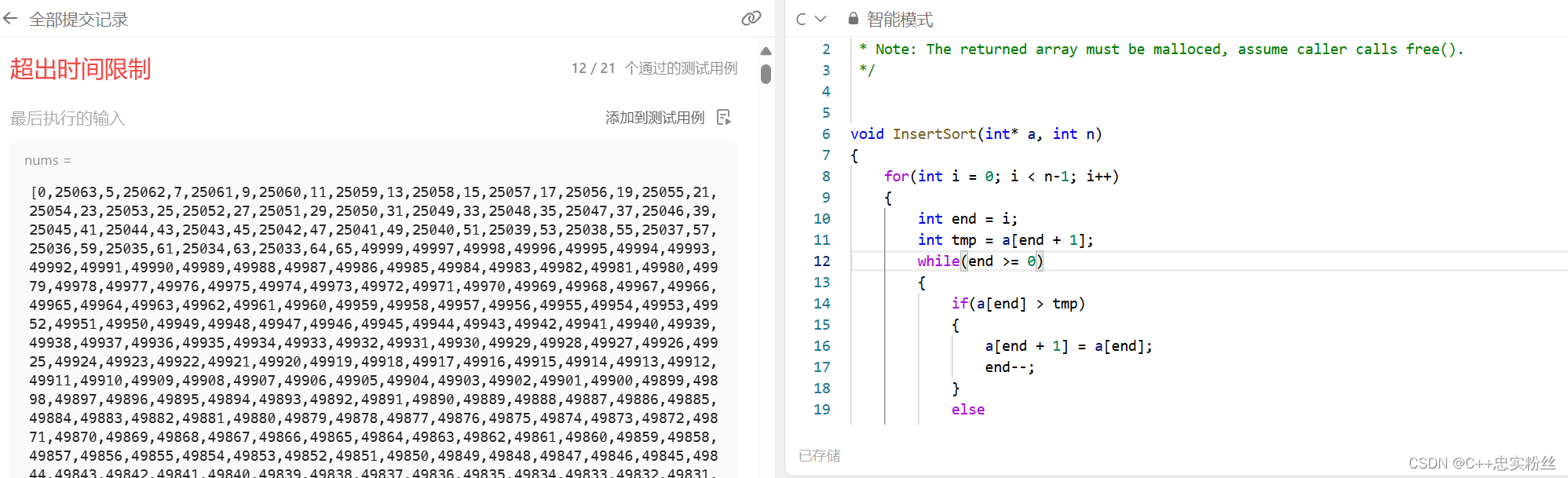
?插入排序可以說是排序的最底層,它最好的情況是有序,時間復雜度為O(n),很顯然這種情況很少見,最壞的情況是逆序,時間復雜度為O(n^2).在平均情況下，直接插入排序的時間復雜度也是 O(n^2)。雖然有時候可能會比較少于最壞情況下的比較次數，但是對于大規模的隨機數組，其平均時間復雜度仍然是二次階的。

在力扣這道題目中只通過了12個例子就超時了.....

直接插入排序的特性總結：

1. 元素集合越接近有序，直接插入排序算法的時間效率越高

2. 時間復雜度：O(N^2)

3. 空間復雜度：O(1)，它是一種穩定的排序算法

4. 穩定性：穩定

2.3希爾排序?( 縮小增量排序 )

2.3.1希爾排序的概念

希爾排序（Shell Sort）是一種改進的插入排序算法，也稱作縮小增量排序。希爾排序通過將原始序列分割成若干個子序列來改善插入排序的性能，每個子序列分別進行插入排序，最后再對整體進行一次插入排序。其基本思想可以描述如下：

步驟：

選擇一個增量序列，通常是使用 Knuth 序列（例如 ( n / 2, n / 4, ..., 1 )）或者 Hibbard 序列（( 2^k - 1 )）來作為增量。
根據選定的增量序列，將待排序的序列分割成若干個子序列。
對每個子序列分別進行插入排序。
逐漸縮小增量，重復以上步驟，直到增量為 1。

排序過程：

假設待排序數組為?[5, 2, 4, 6, 1, 3]。
如果選取增量序列為 ( n / 2, n / 4, ..., 1 )，則初始增量 ( n / 2 = 3 )。
分別對?[5, 6]、[2, 1]、[4, 3]?這三個子序列進行插入排序。
第一次插入排序后，可能得到?[1, 2, 3, 5, 4, 6]。
接下來使用更小的增量進行插入排序，直到最終使用增量為 1 的插入排序完成整體排序。

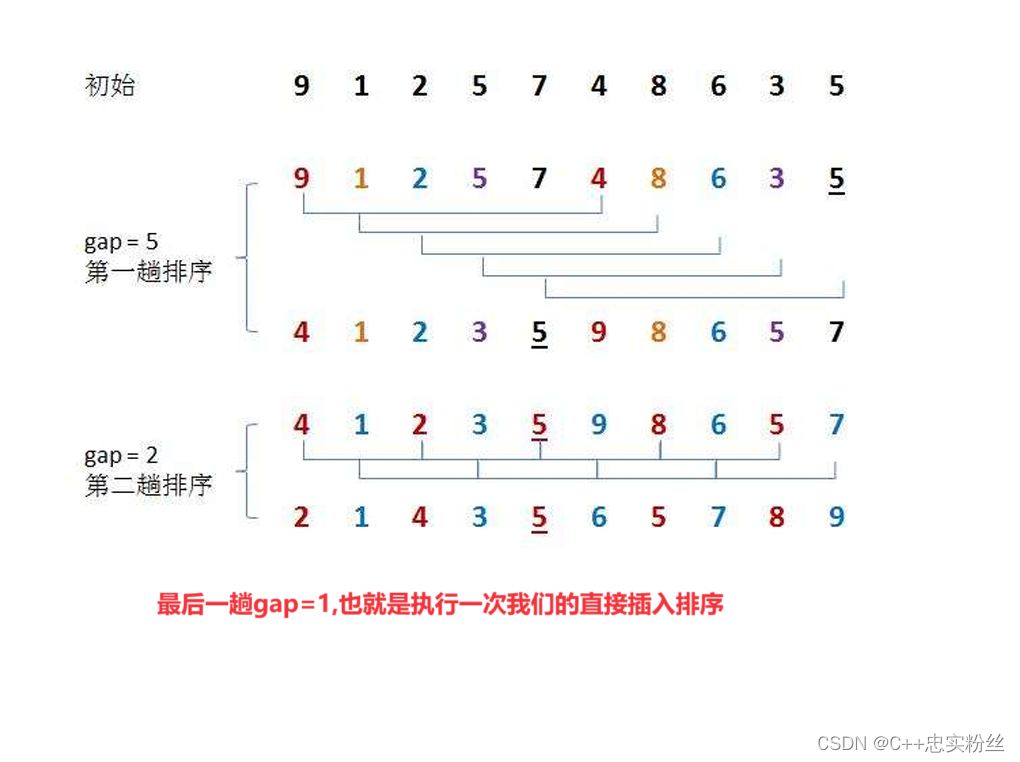
2.3.2希爾排序圖解分析:

2.3.3代碼展示:

void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){// +1保證最后一個gap一定是1// gap > 1時是預排序// gap == 1時是插入排序gap = gap / 3 + 1;for (size_t i = 0; i < n - gap; ++i){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}

代碼邏輯：

初始設置 gap：

初始時，將 gap 設置為數組長度 n。在每一輪迭代中，通過?gap = gap / 3 + 1?逐漸減小 gap 的值，直到最后一次迭代時 gap 等于 1，變成普通的插入排序。

主循環（while 循環）：

當 gap 大于 1 時，進行希爾排序的預處理階段，即根據當前的 gap 進行分組預排序。
當 gap 等于 1 時，執行最后一輪，此時相當于執行普通的插入排序。

預排序階段：

對于每個 gap 值，通過一個 for 循環遍歷數組，對每個分組進行插入排序。這里的?for (size_t i = 0; i < n - gap; ++i)?控制每個分組的起始位置。

插入排序：

對于當前的分組起始位置 i，使用插入排序的方式將該分組內的元素排序。
內部的 while 循環用于找到合適的插入位置，確保當前位置的元素插入到正確的位置。

交換和移動：

如果當前位置的元素比 tmp（待插入元素）大，則將當前位置的元素向后移動 gap 個位置，直到找到合適的插入位置。
插入位置確定后，將 tmp 插入到該位置。

最終結果：

經過多次循環和逐步縮小的 gap 值處理后，數組 a 將被排序完成。

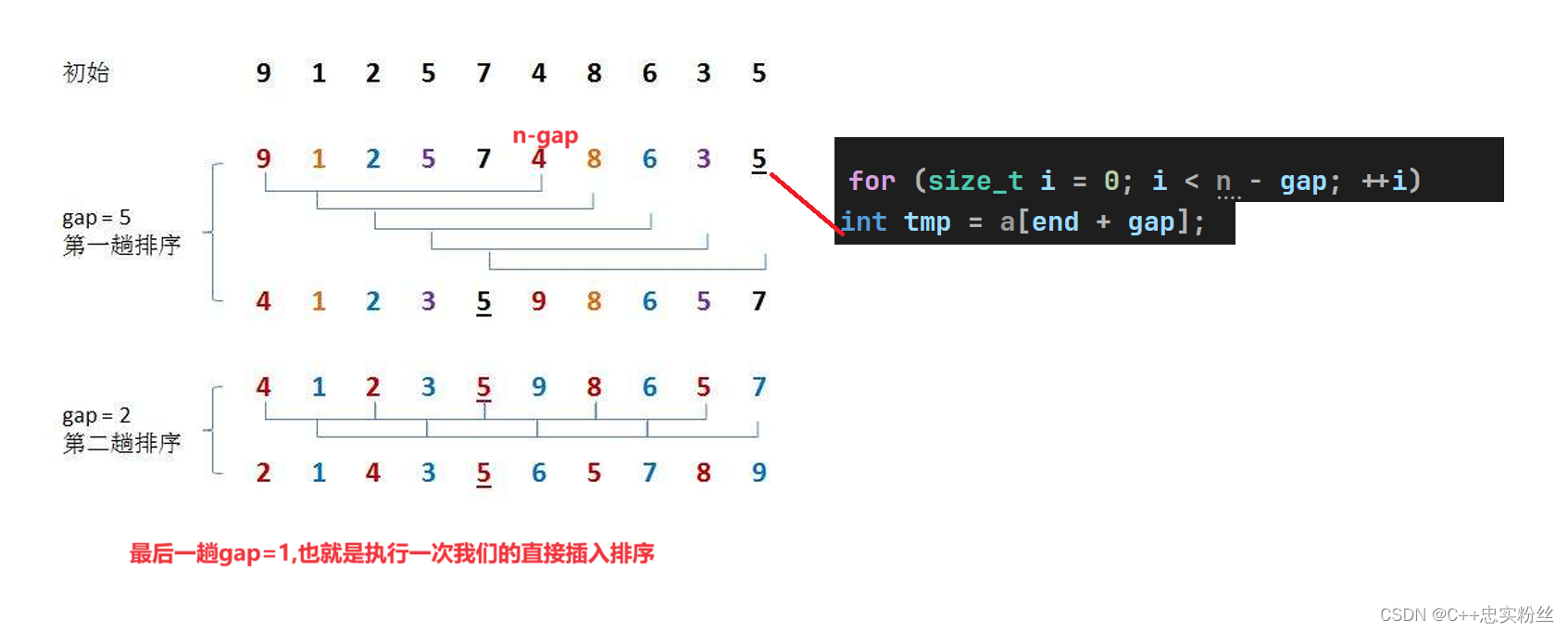
?2.3.4測試代碼:

?測試鏈接:912. 排序數組 - 力扣（LeetCode）

代碼展示:

void ShellSort(int* a, int n)
{int gap = n;while(gap > 1){gap = gap/3 + 1;for(int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while(end >= 0){if(tmp < a[end]){a[end + gap] = a[end];end-=gap;}else{break;}}a[end + gap] = tmp;}}
}int* sortArray(int* nums, int numsSize, int* returnSize) {(*returnSize) = numsSize;int* array = (int*)malloc(sizeof(int)*(*returnSize));for(int i = 0; i < numsSize; i++){array[i] = nums[i];}ShellSort(array, numsSize);return array;
}

結果展示:

居然過了!!!!!!!!!!

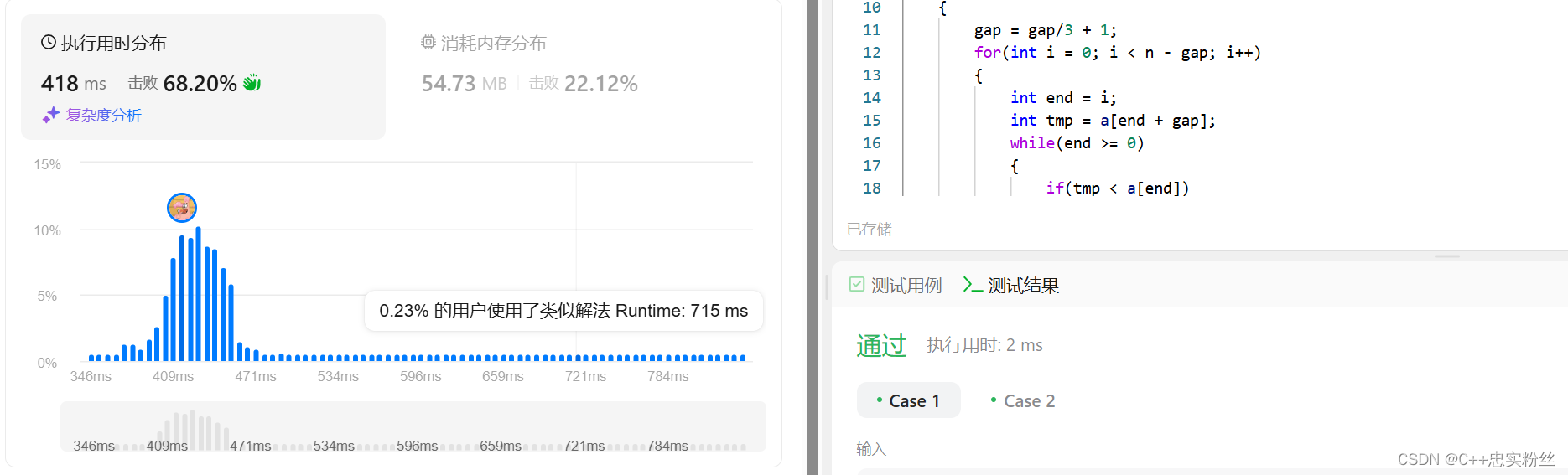
希爾排序雖然有點難理解,看起來很復雜,但是它的效率真的很高.

2.3.5希爾排序時間復雜分析:

?有關希爾排序的時間復雜度至今都沒有定論.

《數據結構(C語言版)》--- 嚴蔚敏

《數據結構-用面相對象方法與C++描述》--- 殷人昆?

因為我的gap是按照Knuth提出的方式取值的，而且Knuth進行了大量的試驗統計，我們暫時就按照：O(n^1.3)來算

那為什么希爾排序的時間復雜難算呢?

第一次預排序?gap = n/3(這里我們將-1省略方便計算),一組有3個數據(n=10),最壞的情況需要排3次,也就是3*3/n=n,也就是說,希爾第一次預排序接近于O(n)

最后一次排序:數組接近有序,可以看成O(n)

第二次預排序:gap=n/9,每組九個數據,最壞的情況(1+2.....+8)*n/9=4n

注意:這里我們第二次預排序取得是最壞的情況,而經過我們第一次得預排序,我們第二次往往不會是最壞的情況,希爾排序難就難在除第一次和最后一次,其他情況是變化的

2.3.6 希爾排序的特性總結：

1. 希爾排序是對直接插入排序的優化。

2. 當gap > 1時都是預排序，目的是讓數組更接近于有序。當gap == 1時，數組已經接近有序的了，這樣就會很快。這樣整體而言，可以達到優化的效果。我們實現后可以進行性能測試的對比。

3. 希爾排序的時間復雜度不好計算，因為gap的取值方法很多，導致很難去計算，因此在好些樹中給出的希爾排序的時間復雜度都不固定：

2.4希爾排序與直接插入排序的關系和比較?

關系與比較：

基礎原理： 希爾排序可以看作是對直接插入排序的改進，通過預處理數據，使其更接近最終排序后的位置，從而減少了直接插入排序中的元素比較和移動次數。

性能比較： 在數據量較小時，直接插入排序可能會比希爾排序更快，因為希爾排序的預處理階段可能帶來一定的額外開銷。但是在大規模數據和隨機數據排序時，希爾排序通常能夠明顯優于直接插入排序。

穩定性： 直接插入排序是穩定的，而希爾排序一般來說是不穩定的，這是因為希爾排序涉及多個子序列的插入排序，子序列之間的相對順序可能發生變化。

綜上所述，希爾排序和直接插入排序雖然在實現上有所區別，但它們的基本思想都是通過逐步將元素移動到正確位置來完成排序，希爾排序通過增量序列的方式優化了插入排序的性能，特別是在處理大規模數據時表現更為優越。