引言

介紹動態規劃（DP）在解決子數組問題上的重要性，以及本文的目的——通過具體問題的分析和代碼示例，幫助讀者理解如何用DP解決子數組問題。

子數組問題介紹

簡要介紹什么是子數組問題，以及這些問題在實際應用中的重要性。例如，最大子數組和問題、最長遞增子數組問題等。

動態規劃的基本概念

解釋動態規劃的基本思想：通過將問題分解為子問題，保存子問題的解來避免重復計算，從而提高算法效率。可以簡單介紹狀態、狀態轉移方程和初始條件等基本概念。

具體問題的解決方法

最大子數組和問題（Maximum Subarray Sum）
問題描述：
給定一個整數數組，找出和最大的連續子數組，并返回其最大和。

動態規劃解法：

定義狀態：dp[i]表示以第i個元素結尾的最大子數組和。
狀態轉移方程：dp[i] = max(nums[i], dp[i-1] + nums[i])
即對于第i個元素，最大子數組和要么是自己，要么是前一個元素的最大子數組和加上自己。
初始狀態：dp[0] = nums[0]
結果：max(dp)，即所有dp[i]中的最大值。

關于子數組問題的幾個題

1.最大子數組和

題目鏈接
題目：

樣例輸出和輸入：

題目要求很簡單，就是求出 最長的子數組的和，這個和有一個要求就是和最大。
算法原理：
狀態表示：dp[i]表示以i位置為結尾時所有子數組的和中最大的那個。
狀態轉移方程：
分析：到達i位置時i位置最長的子數組的和應該等于i-1位置的最長子數組的和加上當前i位置的值，還有一種情況：單獨分析，就是當前位置的數就是一個子數組，長度為1，所以，dp[i]=max(dp[i-1]+nums[i],nums[i])。
代碼展示：

class Solution {
public:int maxSubArray(vector<int>& nums){int n = nums.size();vector<int> dp(n);dp[0] = nums[0];for (int i = 1;i < n;i++){dp[i] = max(dp[i - 1] + nums[i], nums[i]);}int  Max = -0x3f3f3f3f;for (int i = 0;i < n;i++){Max = max(dp[i], Max);}return Max;}
};

運行結果：

2.環形子數組的最大和

題目鏈接
題目：

樣例輸出和輸入：

這道題在第一道題的基礎上加了一個條件，就是這是個環形數組頭和尾是相連的。也讓我們求子數組中和最大的那個。
算法原理：
狀態表示：分析：明顯這道題一個狀態是表示不了的，因為這個子數組可能連續也可能不連續，由于求的最大的值，所以第一種情況：當子數組在中間時最大，還有一種情況，子數組在兩邊時不連續的時候最大 ，當不連續的時候 最大，也就是中間的最小。這兩種狀態分別為f[i]和g[i]。

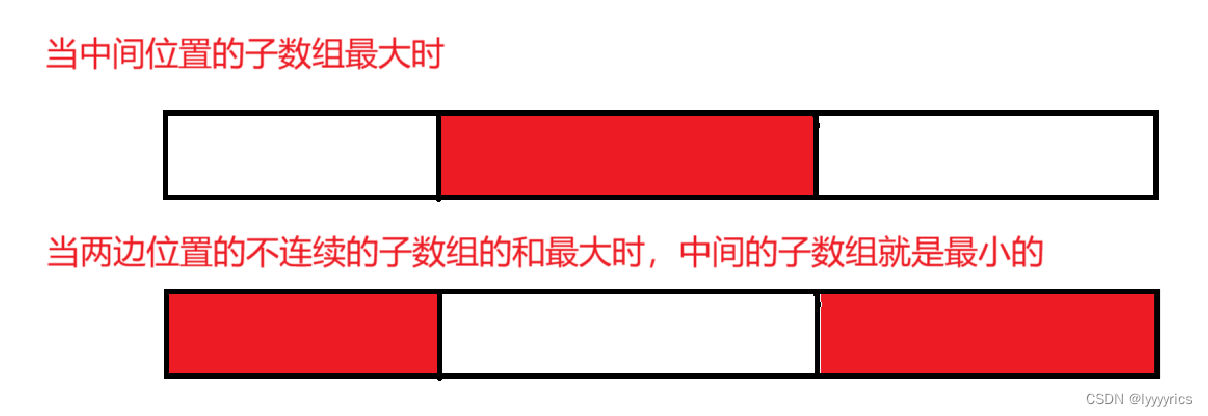
狀態轉移方程：先分析中間最大的時候的狀態，當到達i位置的時候i位置的最大的子數組的和就是前一個位置i-1的位置的最大的子數組的和加上當前i位置的值，還有一種情況就是i位置自身成一個長度為1的數組。f[i] = max(f[i - 1] + nums[i-1], nums[i-1])，g[i]也同理，g[i]為當前位置的子數組中最小的那個 子數組的和，所以i位置的子數組和的最小等于前一個位置的子數組和的最小，加上當前位置，g[i - 1] + nums[i-1]最后還要取一個min，g[i] = min(g[i - 1] + nums[i-1], nums[i-1])

代碼展示：

class Solution {
public:int maxSubarraySumCircular(vector<int>& nums){int n = nums.size();vector<int> f(n + 1), g(n + 1);int sum = 0;int fmax = INT_MIN;int gmin = INT_MAX;for (int i = 1;i <= n;i++){f[i] = max(f[i - 1] + nums[i-1], nums[i-1]);fmax = max(f[i], fmax);g[i] = min(g[i - 1] + nums[i-1], nums[i-1]);gmin = min(gmin, g[i]);sum += nums[i - 1];}return sum == gmin ? fmax : max(fmax, sum - gmin);}
};

運行結果：

3.乘積最大子數組

題目鏈接
題目：

樣例輸出和輸入：

這道題的題意和前兩道題也大差不差，就是讓我們求最大乘積的子數組的乘積。
算法原理：
狀態表示：這道題還是需要兩個狀態，因為有負數情況，不一定是正數乘正數才是最大的，兩個負數相乘也 有可能是最大的。f[i]表示以i位置為結尾的子數組中的最大乘積的那個，g[i]表示以i位置為結尾的子數組中最小的乘積的那個。
狀態轉移方程：首先分析f[i]這個狀態，這個狀態有三個子狀態，第一種狀態是i位置是負數時，所以負數應乘上最小的才是最大的，還有一種狀態就是當前位置是正數，所以當前位置應該乘上前一個位置中最大的那個子數組的乘積。還有一個情況就是單獨成為一個子數組。

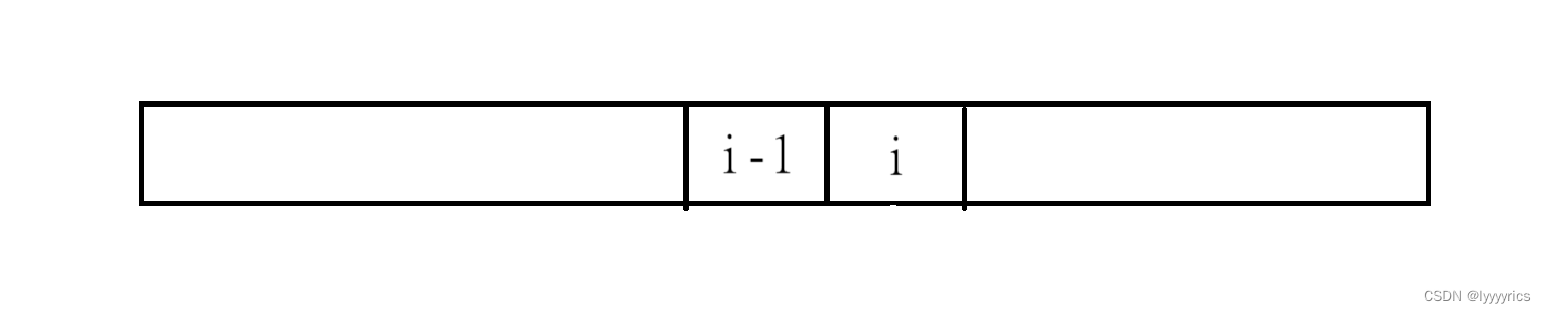
max(nums[i - 1], max(f[i - 1] * nums[i - 1], g[i - 1] * nums[i - 1]))
g[i]的狀態轉移方程也可以用類似的方法進行分析：min(nums[i - 1], min(f[i - 1] * nums[i - 1], g[i - 1] * nums[i - 1]))

代碼展示：

class Solution {
public:int maxProduct(vector<int>& nums){int n = nums.size();vector<double> f(n + 1), g(n + 1);//f是最大的，g是最小的g[0] = 1, f[0] = 1;double ret = INT_MIN;for (int i = 1;i <= n;i++){double x = nums[i - 1], y = f[i - 1] * nums[i - 1], z = g[i - 1] * nums[i - 1];f[i] = max(x, max(y, z));g[i] = min(x, min(y, z));ret = max(f[i], ret);}return ret;}
};

運行結果：

4.乘積為正數的最長子數組長度

題目鏈接
題目：

樣例輸出和輸入：

這道題要求的是乘積是正數的子數組總長度最長的那個子數組的長度。
算法原理：
狀態表示：由于兩個負數相乘也是正數，所以狀態表示的時候我們也要記錄負數的狀態，f[i]表示以i位置為結尾的所有子數組中乘積是正數的最長的子數組的長度，g[i]]是以i位置為結尾的子數組中乘積為負數的最長子數組的長度。
狀態轉移方程：需要判斷i位置的值是正數還是負數，如果是負數的話就是就需要用前一個位置的負數子數組的最長的那個加一，也就是g[i-1]+1但是前i-1個有可能沒有小于零的，所以這里f[i]是有可能是零的，所以這里需要判斷一下i-1位置時的g[i-1]的值，當當前值大于零的時候f[i]就等于 前一個位置的f[i-1]+1,同理負數的最長子數組也可以分析出來，狀態轉移方程：這是大于零的兩種狀態的情況：g[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1，f[i] = f[i - 1] + 1小于零的兩種狀態的情況：f[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1，g[i] = f[i - 1] + 1。

代碼展示：

class Solution {
public:int getMaxLen(vector<int>& nums) {int n = nums.size();if (n == 1){return nums[0] > 0;}vector<int> f(n), g(n);f[0] = nums[0] > 0, g[0] = nums[0] < 0;int fmax = 0;for (int i = 1;i < n;i++){if (nums[i] > 0){f[i] = f[i - 1] + 1;g[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;fmax = max(f[i], fmax);}else if (nums[i] < 0){f[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;g[i] = f[i - 1] + 1;fmax = max(f[i], fmax);}}return fmax;}
};

運行結果：

5.等差數列劃分

題目鏈接
題目：

樣例輸出和輸入：

這道題題意很簡單，就是讓我們求所有能構成等差數列的子數組的總和
算法原理：
等差數列性質：2a=c+ba為等差中項。
狀態表示：dp[i]為以i位置為結尾的所有子數組中的等差數列的個數。
狀態轉移方程：先判斷i位置的前兩個位置是否 滿足上述的等差數列的性質：如果滿足則dp[i]=dp[i - 1] + 1因為滿足，所以dp[i-1]位置需要算上，但是又多了一個子數組，這個子數組 就是滿足的那個三個數的子數組。不滿足的話,dp[i]直接就是0.
代碼展示：

class Solution {
public:int numberOfArithmeticSlices(vector<int>& nums) {int n = nums.size();if (n < 3){return  0;}vector<int>  dp(n);dp[0] = 0, dp[1] = 0;int count = 0;for (int i = 2;i < n;i++){dp[i] = nums[i] + nums[i - 2] == 2 * nums[i - 1] ? dp[i - 1] + 1 : 0;}for(int i=0;i<n;i++){count+=dp[i];}return count;}
};

運行結果：

總結

通過本文的介紹，我們詳細探討了動態規劃在解決子數組問題中的應用，具體分析了最大子數組和問題和最長遞增子數組問題。這些問題在實際生活中的數據處理、優化等場景中有著廣泛的應用。動態規劃通過將問題分解為子問題，保存子問題的解，避免了重復計算，從而大大提高了算法的效率。

在學習和應用動態規劃的過程中，我們需要明確狀態、狀態轉移方程和初始條件。通過練習具體問題，我們可以更深入地理解動態規劃的思想和方法。無論是最大子數組和問題還是最長遞增子數組問題，掌握了動態規劃的基本原理后，我們可以更靈活地應對其他類似的問題。

希望這篇文章能幫助你更好地理解動態規劃在子數組問題中的應用。如果你有任何問題或建議，歡迎在評論區留言，我們將盡力為你解答。祝你在學習動態規劃和解決實際問題的過程中取得更多的進步！