????????我將我倉庫里的排序算法給大家匯總整理了一下，寫的非常非常細，還對每個算法制作了動畫，一定能夠對大家有所幫助，歡迎大家閱讀。另外我也對 leetcode 上面可以用排序算法秒殺的算法題進行了總結，會在后面的文章中進行發布，歡迎大家閱讀。

????????另外大家如果需要其他動畫題解的話，可以看下這個倉庫，大概 100 來張動畫了
GitHub - chefyuan/algorithm-base: 一位酷愛做飯的程序員，立志用動畫將算法說的通俗易懂。我的面試網站 www.chengxuchu.com

@

目錄

• 實際應用及排序算法詳解
• 冒泡排序（Bubble Sort）
  • 最簡單的排序實現
  • 改進
• 簡單選擇排序
• 希爾排序 （Shell's Sort）
• 快速排序
  • 挖坑填數
  • 交換位置
  • 快速排序的迭代寫法
  • 快速排序優化
    • 三數取中法
    • 三數取中法
    • 和插入排序搭配使用
    • 三數取中+插入排序
    • 三數取中+三向切分+插入排序
• 堆排序
  • 利用上浮操作建堆
  • 下沉建堆
• 歸并排序
  • 遞歸實現
  • 迭代實現
• 計數排序

實際應用及排序算法詳解

寫在前面

????????袁記菜館內

袁廚：小二，最近快要過年了，咱們店也要給大家發點年終獎啦，你去根據咱們的紅黑豆小本本，看一下大家都該發多少的年終獎，然后根據金額從小到大排好，按順序一個一個發錢，大家回去過個好年，你也老大不小了，回去取個媳婦。

小二：好滴掌柜的，我現在馬上就去。

????????我用過的一些還不錯的算法資料，大家也可以看一哈，個人認為很不錯，一定會對你有所幫助。
下載地址

????????上面說到的按照金額從大到小排好就是我們今天要講的內容 --- 排序。

????????排序是我們生活中經常會面對的問題，體育課的時候，老師會讓我們從矮到高排列，考研錄取時，成績會按總分從高到底進行排序（考研的各位讀者，你們必能收到心儀學校給你們寄來的大信封），我們網購時，有時會按銷量從高到低，價格從低到高，將最符合咱們預期的商品列在前面。

????????概念：將雜亂無章的數據元素，通過一定的方法（排序算法）按關鍵字（k）順序排列的過程叫做排序。例如我們上面的銷量和價格就是關鍵字

排序算法的穩定性

????????什么是排序算法的穩定性呢？

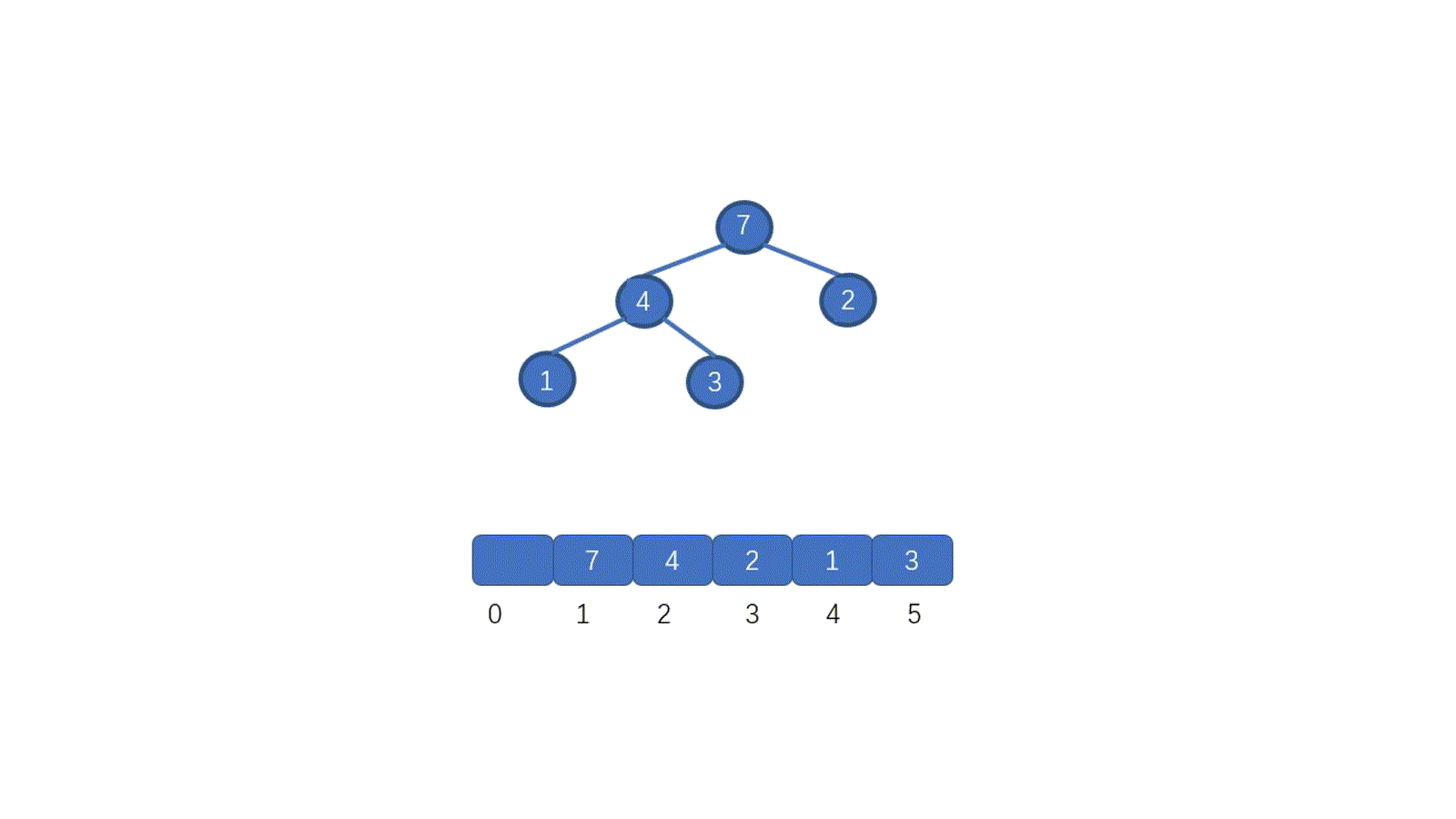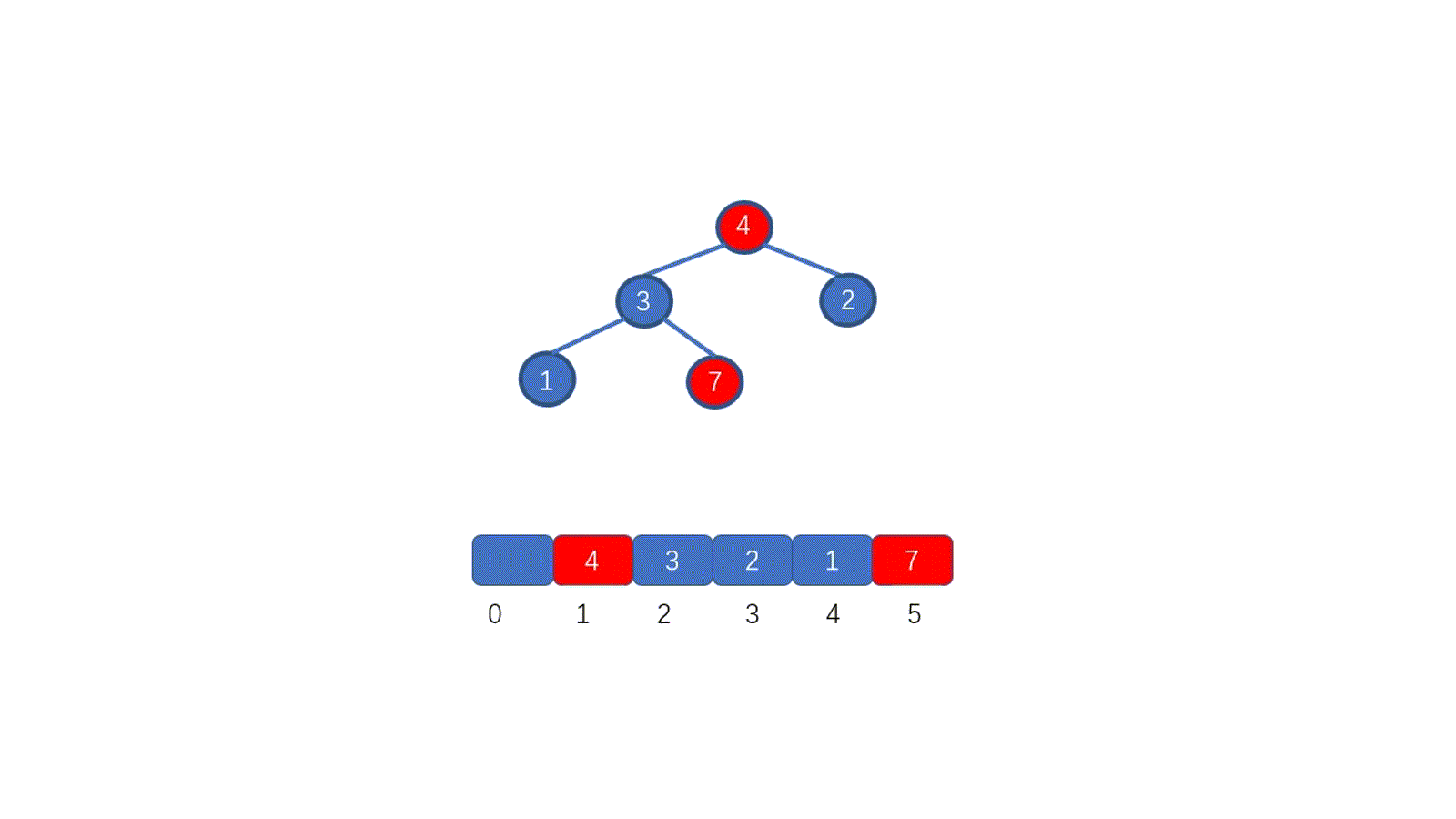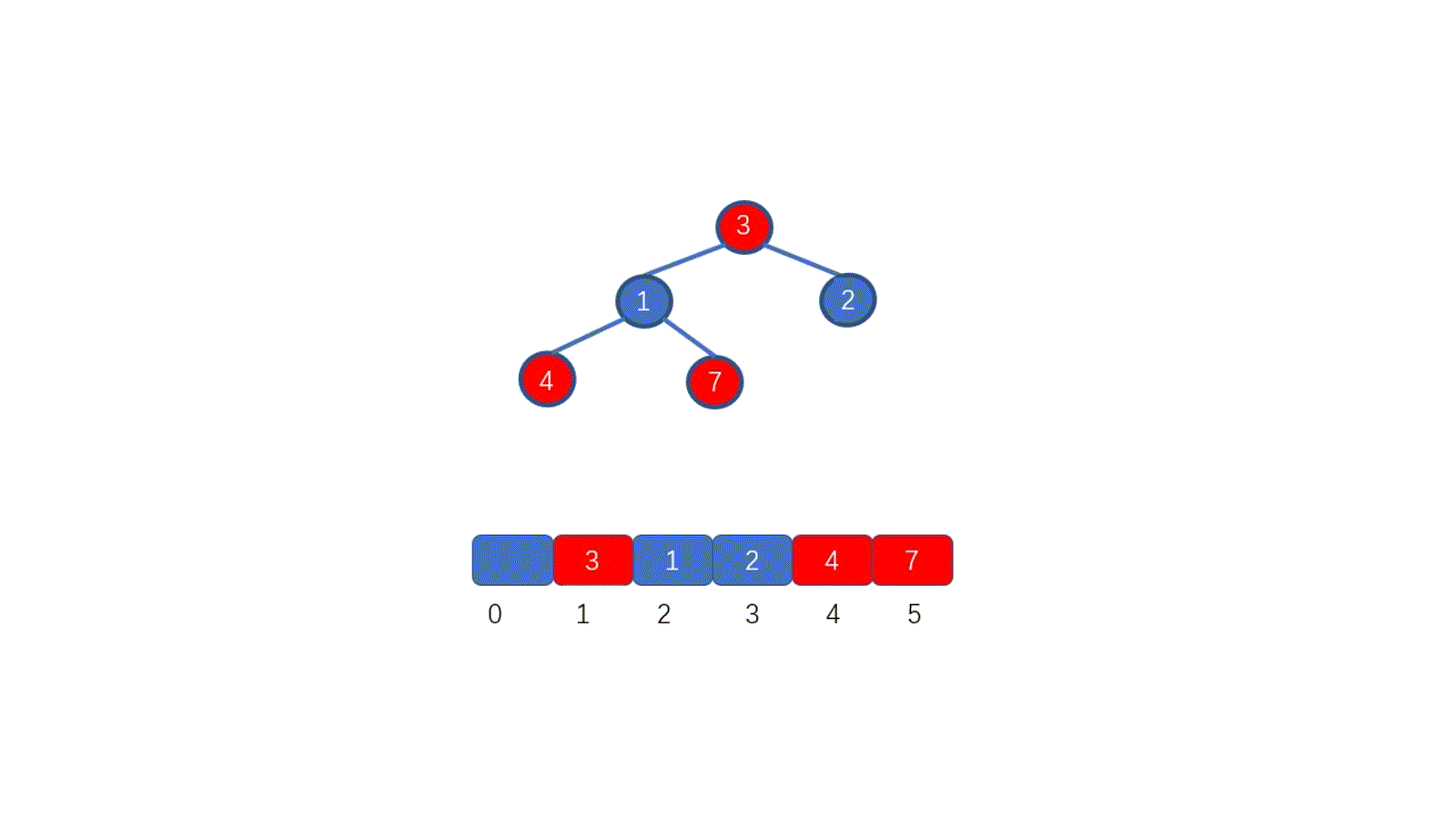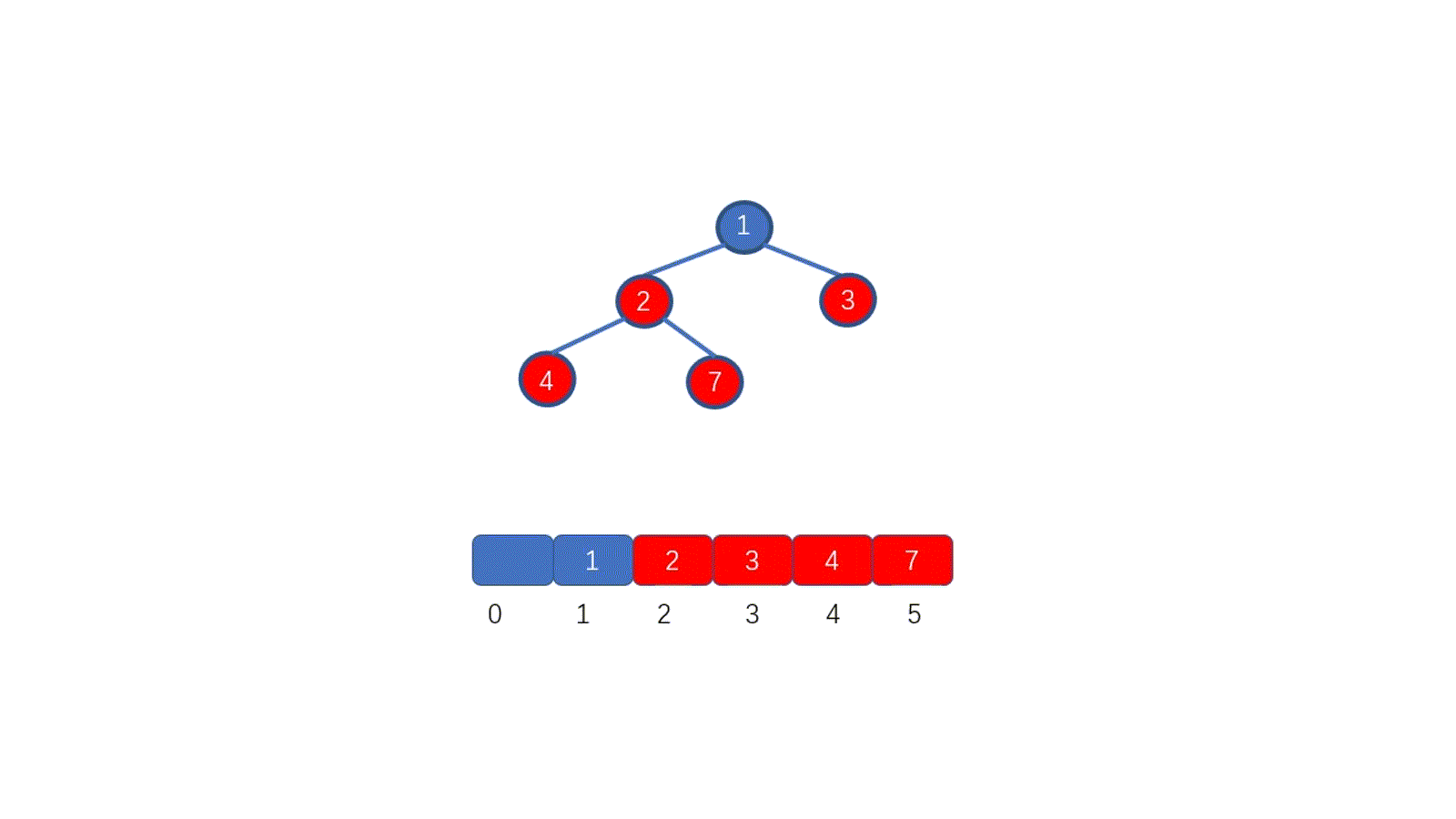
????????因為我們待排序的記錄序列中可能存在兩個或兩個以上的關鍵字相等的記錄，排序結果可能會存在不唯一的情況，所以我們排序之后，如果相等元素之間原有的先后順序不變。則稱所用的排序方法是穩定的，反之則稱之為不穩定的。見下圖

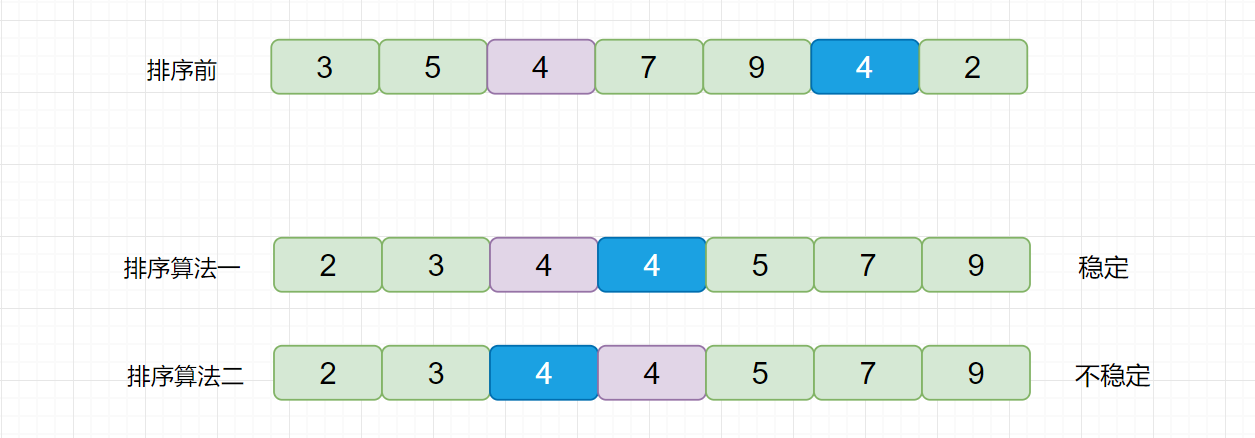
????????例如上圖，我們的數組中有兩個相同的元素 4， 我們分別用不同的排序算法對其排序，算法一排序之后，兩個相同元素的相對位置沒有發生改變，我們則稱之為穩定的排序算法，算法二排序之后相對位置發生改變，則為不穩定的排序算法。

那排序算法的穩定性又有什么用呢？

????????在我們做題中大多只是將數組進行排序，只需考慮時間復雜度空間復雜度等指標，排序算法是否穩定，一般不進行考慮。但是在真正軟件開發中排序算法的穩定性是一個特別重要的衡量指標。繼續說我們剛才的例子。我們想要實現年終獎從少到多的排序，然后相同年終獎區間內的紅豆數也按照從少到多進行排序。

????????排序算法的穩定性在這里就顯得至關重要。這是為什么呢？見下圖

????????第一次排序之后，所有的職工按照紅豆數從少到多有序。

????????第二次排序中，我們使用穩定的排序算法，所以經過第二次排序之后，年終獎相同的職工，仍然保持著紅豆的有序（想對位置不變），紅豆仍是從小到大排序。我們使用穩定的排序算法，只需要兩次排序即可。

????????穩定排序可以讓第一個關鍵字排序的結果服務于第二個關鍵字排序中數值相等的那些數。

????????上述情況如果我們利用不穩定的排序算法，實現這一效果是十分復雜的。

比較類和非比較類

????????我們根據元素是否依靠與其他元素的比較來決定元素間的相對次序。以此來區分比較類排序算法和非比較類排序算法。

內排序和外排序

????????內排序是在排序的整個過程中，待排序的所有記錄全部被放置在內存中。外排序是由于排序的記錄個數太多，不能同時放置在內存中，整個排序過程需要在內外存之間多次交換數據才能進行，常見的內部排序算法有：插入排序、希爾排序、選擇排序、冒泡排序、歸并排序、快速排序、堆排序、基數排序等。

????????對我們內排序來說，我們主要受三個方面影響，時間性能，輔助空間，算法的復雜性

時間性能

????????在我們的排序算法執行過程中，主要執行兩種操作比較和交換，比較是排序算法最起碼的操作，移動指記錄從一個位置移動到另一個位置。所以我們一個高效的排序算法，應該盡可能少的比較和移動。

輔助空間

????????執行算法所需要的輔助空間的多少，也是來衡量排序算法性能的一個重要指標

算法的復雜度

????????這里的算法復雜度不是指算法的時間復雜度，而是指算法本身的復雜度，過于復雜的算法也會影響排序的性能。

????????下面我們一起復習兩種簡單排序算法，冒泡排序和簡單選擇排序，看看有沒有之前忽略的東西。

冒泡排序（Bubble Sort）

????????估計我們在各個算法書上介紹排序時，第一個估計都是冒泡排序。主要是這個排序算法思路最簡單，也最容易理解，（也可能是它的名字好聽，哈哈），學過的老哥們也一起來復習一下吧，我們一起深挖一下冒泡排序。

????????冒泡排序的基本思想是，兩兩比較相鄰記錄的關鍵字，如果是反序則交換，直到沒有反序為止。冒泡一次冒泡會讓至少一個元素移動到它應該在的位置，那么如果數組有 n 個元素，重復 n 次后則能完成排序。根據定義可知那么冒泡排序顯然是一種比較類排序。

最簡單的排序實現

我們來看一下這段代碼

class Solution {public int[] sortArray(int[] nums) {int len = nums.length;for (int i = 0; i < len; ++i) {for (int j = i+1; j < len; ++j) {if (nums[i] > nums[j]) {swap(nums,i,j);}}}return nums;}public void swap(int[] nums,int i,int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}
}

????????我們來思考一下上面的代碼，每次讓關鍵字 nums[i] 和 nums[j] 進行比較如果 nums[i] > nums[j] 時則進行交換，這樣 nums[0] 在經過一次循環后一定為最小值。那么這段代碼是冒泡排序嗎？

????????顯然不是，我們冒泡排序的思想是兩兩比較相鄰記錄的關鍵字，注意里面有相鄰記錄，所以這段代碼不是我們的冒泡排序，下面我們用動圖來模擬一下冒泡排序的執行過程，看完之后一定可以寫出正宗的冒泡排序。

題目代碼

class Solution {public int[] sortArray(int[] nums) {int len = nums.length;for (int i = 0; i < len; ++i) {for (int j = 0; j < len - i - 1; ++j) {if (nums[j] > nums[j+1]) {swap(nums,j,j+1);}}}return nums;       }public void swap(int[] nums,int i,int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}
}

改進

上圖中的代碼則為正宗的冒泡排序代碼，但是我們是不是發現了這個問題

????????我們此時數組已經完全有序了，可以直接返回，但是動圖中并沒有返回，而是繼續執行，那我們有什么辦法讓其完全有序時，直接返回，不繼續執行嗎？

????????我們設想一下，我們是通過 nums[j] 和 nums[j+1] 進行比較，如果大于則進行交換，那我們設想一下，如果一個完全有序的數組，我們進行冒泡排序，每次比較發現都不用進行交換。

????????那么如果沒有交換則說明當前完全有序。那我們可不可以通過一個標志位來進行判斷是否發生了交換呢？當然是可以的

冒泡排序改進

class Solution {public int[] sortArray(int[] nums) {int len = nums.length;//標志位boolean flag = true;//注意看 for 循環條件for (int i = 0; i < len && flag; ++i) {//如果沒發生交換，則依舊為false，下次就會跳出循環flag = false;for (int j = 0; j < len - i - 1; ++j) {if (nums[j] > nums[j+1]) {swap(nums,j,j+1);//發生交換，則變為true,下次繼續判斷flag = true;}}          }return nums;}public void swap(int[] nums,int i,int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}
}

????????這樣我們就避免掉了已經有序的情況下無意義的循環判斷。

冒泡排序時間復雜度分析

????????最好情況，就是要排序的表完全有序的情況下，根據改進后的代碼，我們只需要一次遍歷即可，只需 n -1 次比較，時間復雜度為 O(n)。最壞情況時，即待排序表逆序的情況，則需要比較(n-1) + (n-2) +.... + 2 + 1= n(n-1)/2 ，并等量級的交換，則時間復雜度為O(n^2)。

????????平均情況下，需要 n(n-1)/4 次交換操作，比較操作大于等于交換操作，而復雜度的上限是 O(n^2)，所以平均情況下的時間復雜度就是 O(n^2)。

冒泡排序空間復雜度分析

????????因為冒泡排序只是相鄰元素之間的交換操作，只用到了常量級的額外空間，所以空間復雜度為 O(1)

冒泡排序穩定性分析

????????那么冒泡排序是穩定的嗎？當然是穩定的，我們代碼中，當 nums[j] > nums[j + 1] 時，才會進行交換，相等時不會交換，相等元素的相對位置沒有改變，所以冒泡排序是穩定的。

算法名稱	最好時間復雜度	最壞時間復雜度	平均時間復雜度	空間復雜度	是否穩定
冒泡排序	O(n)	O(n^2)	O(n^2)	O(1)	穩定

---

簡單選擇排序

????????我們的冒泡排序不斷進行交換，通過交換完成最終的排序，我們的簡單選擇排序的思想也很容易理解，主要思路就是我們每一趟在 n-i+1 個記錄中選取關鍵字最小的記錄作為有序序列的第 i 個記錄。

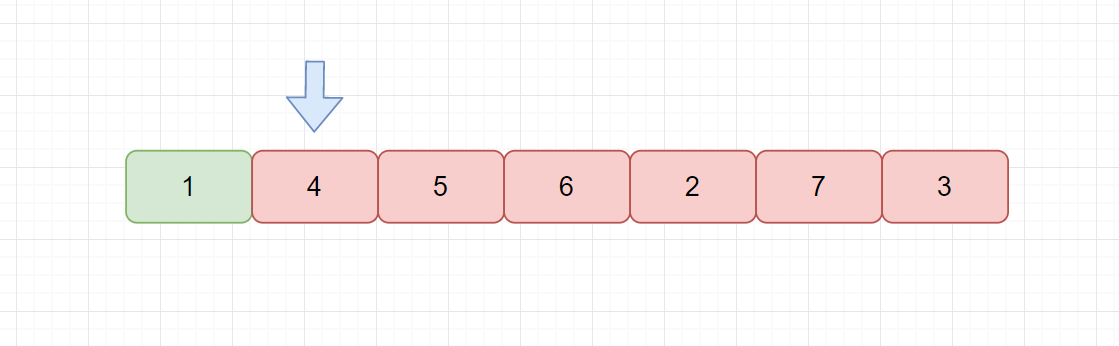
????????例如上圖，綠色代表已經排序的元素，紅色代表未排序的元素。我們當前指針指向 4 ，則我們遍歷紅色元素，從中找到最小值，然后與 4 交換。我們發現選擇排序執行完一次循環也至少可以將 1 個元素歸位。

????????下面我們來看一下代碼的執行過程，看過之后肯定能寫出代碼的。

注：我們為了更容易理解，min 值保存的是值，而不是索引，實際代碼中保存的是索引

簡單選擇排序代碼

class Solution {public int[] sortArray(int[] nums) {int len = nums.length;int min = 0;for (int i = 0; i < len; ++i) {min = i;//遍歷到最小值for (int j = i + 1; j < len; ++j) {              if (nums[min] > nums[j]) min = j;              }if (min != i) swap(nums,i,min);        }return nums;}public void swap (int[] nums, int i, int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}
}

簡單選擇排序時間復雜度分析

????????從簡單選擇排序的過程來看，他最大的特點就是交換移動數據次數相當少，這樣也就節省了排序時間，簡單選擇和冒泡排序不一樣，我們發現無論最好情況和最壞情況，元素間的比較次數是一樣的，第 i 次排序，需要 n - i 次比較,n 代表數組長度，則一共需要比較(n-1) + (n-2) +.... + 2 + 1= n*(n-1)/2 次，對于交換而言，最好情況交換 0 次，最壞情況(逆序時)交換 n - 1次。那么簡單選擇排序時間復雜度也為 O(n^2) 但是其交換次數遠小于冒泡排序，所以其效率是好于冒泡排序的。

簡單選擇排序空間復雜度分析

????????由我們動圖可知，我們的簡單選擇排序只用到了常量級的額外空間，所以空間復雜度為 O(1)。

簡單選擇排序穩定性分析

????????我們思考一下，我們的簡單選擇排序是穩定的嗎？顯然不是穩定的，因為我們需要在指針后面找到最小的值，與指針指向的值交換，見下圖。

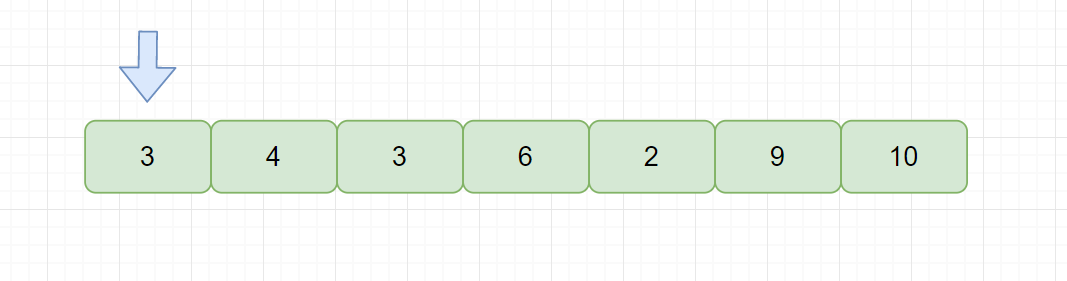
????????此時我們需要從后面元素中找到最小的元素與指針指向元素交換，也就是元素 2 。但是我們交換后發現，兩個相等元素 3 的相對位置發生了改變，所以簡單選擇排序是不穩定的排序算法。

算法名稱	最好時間復雜度	最壞時間復雜度	平均時間復雜度	空間復雜度	是否穩定
簡單選擇排序	O(n^2)	O(n^2)	O(n^2)	O(1)	不穩定

---

## 直接插入排序（Straight Insertion Sort）

袁記菜館內

袁廚：好嘞，我們打烊啦，一起來玩會撲克牌吧。

小二：好啊，掌柜的，咱們玩會斗地主吧。

相信大家應該都玩過撲克牌吧，我們平常摸牌時，是不是一邊摸牌，一邊理牌，摸到新牌時，會將其插到合適的位置。這其實就是我們的插入排序思想。

直接插入排序：將一個記錄插入到已經排好序的有序表中，從而得到一個新的有序表。通俗理解，我們首先將序列分成兩個區間，有序區間和無序區間，我們每次在無序區間內取一個值，在已排序區間中找到合適的插入位置將其插入，并保證已排序區間一直有序。下面我們看一下動圖吧。

注：為了更清晰表達算法思想，則采用了挖掉待排序元素的形式展示，后面也會采取此形式表達。

另外關于這個算法對鏈表的排序大家可以去這個倉庫看一哈鏈表插入排序

直接插入排序代碼

class Solution {public int[] sortArray(int[] nums) {//注意 i 的初始值為 1，也就是第二個元素開始for (int i = 1; i < nums.length; ++i) {//待排序的值int temp = nums[i];//需要注意int j;for (j = i-1; j >= 0; --j) {//找到合適位置if (temp < nums[j]) {nums[j+1] = nums[j];continue;} //跳出循環break;}//插入到合適位置，這也就是我們沒有在 for 循環內定義變量的原因nums[j+1] = temp;}return nums;}
}

直接插入排序時間復雜度分析

????????最好情況時，也就是有序的時候，我們不需要移動元素，每次只需要比較一次即可找到插入位置，那么最好情況時的時間復雜度為O(n)。

????????最壞情況時，即待排序表是逆序的情況，則此時需要比較2+3+....+n = (n+2)(n-1)/2,移動次數也達到了最大值，3 +4+5+....n+1 = (n+4)(n-1)/2,時間復雜度為O(n^2).

????????我們每次插入一個數據的時間復雜度為O(n)，那么循環執行 n 次插入操作，平均時間復雜度為O(n^2)。

直接插入排序空間復雜度分析

????????根據動畫可知，插入排序不需要額外的存儲空間，所以其空間復雜度為O(1)

直接插入排序穩定性分析

????????我們根據代碼可知，我們只會移動比 temp 值大的元素，所以我們排序后可以保證相同元素的相對位置不變。所以直接插入排序為穩定性排序算法。

---

希爾排序 （Shell's Sort）

????????我們在之前說過直接插入排序在記錄基本有序的時候和元素較少時效率是很高的，基本有序時，只需執行少量的插入操作，就可以完成整個記錄的排序工作。當元素較少時，效率也很高，就比如我們經常用的 Arrays.sort (),當元素個數少于47時，使用的排序算法就是直接插入排序。那么直接希爾排序和直接插入排序有什么關系呢？

????????希爾排序是插入排序的一種，又稱“縮小增量排序”（Diminishing Increment Sort），是直接插入排序的高級變形，其思想簡單點說就是有跨度的插入排序，這個跨度會逐漸變小，直到變為 1，變為 1 時記錄也就基本有序，這時用到的也就是我們之前講的直接插入排序了。

基本有序：就是小的關鍵字基本在前面，大的關鍵字基本在后面，不大不小的基本在中間。見下圖。

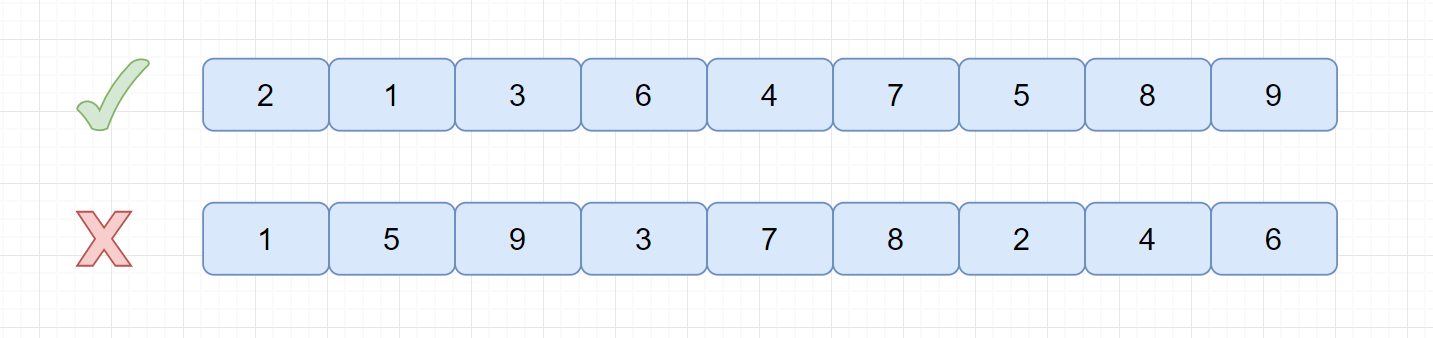
我們已經了解了希爾排序的基本思想，下面我們通過一個繪圖來描述下其執行步驟。

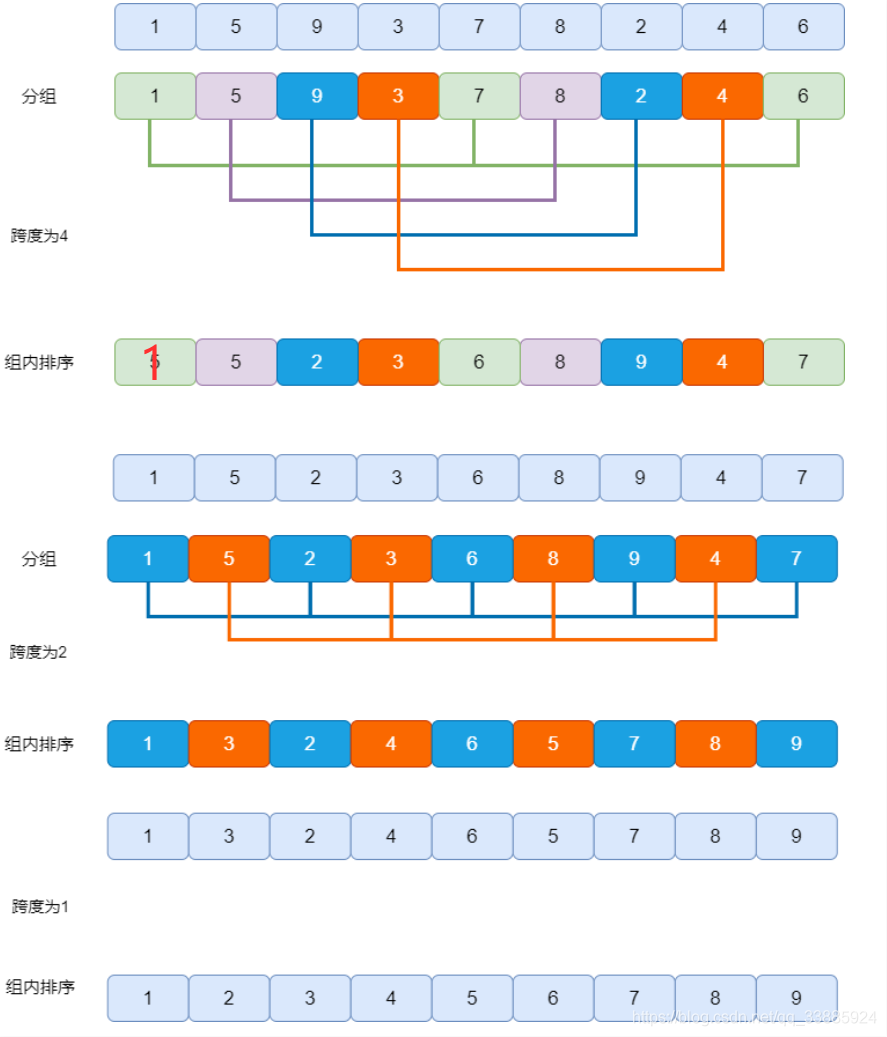
????????先逐步分組進行粗調，在進行直接插入排序的思想就是希爾排序。我們剛才的分組跨度（4，2，1）被稱為希爾排序的增量，我們上面用到的是逐步折半的增量方法，這也是在發明希爾排序時提出的一種樸素方法，被稱為希爾增量，下面我們用動圖模擬下使用希爾增量的希爾排序的執行過程

????????[外鏈圖片轉存失敗,源站可能有防盜鏈機制,建議將圖片保存下來直接上傳(img-7kcFzlRK-1621395235780)(https://cdn.jsdelivr.net/gh/tan45du/test1@master/20210122/希爾排序.4vxwr7bkbjw0.gif)]

????????大家可能看了視頻模擬，也不是特別容易寫出算法代碼，不過你們看到代碼肯定會很熟悉滴。

希爾排序代碼

class Solution {public int[] sortArray(int[] nums) {int increment = nums.length;//注意看結束條件while (increment > 1) {//這里可以自己設置increment = increment / 2;//根據增量分組for (int i = 0; i < increment; ++i) {//這快是不是有點面熟，回去看看咱們的插入排序for (int j = i + increment; j < nums.length; j += increment) {int temp = nums[j];int k;for (k = j - increment; k >= 0; k -= increment) {if (temp < nums[k]) {nums[k+increment] = nums[k];continue;}break;}nums[k+increment] = temp;}}}return nums;}
}

????????我們剛才說，我們的增量可以自己設置的，我們上面的例子是用的希爾增量，下面我們看這個例子，看看使用希爾增量會出現什么問題。

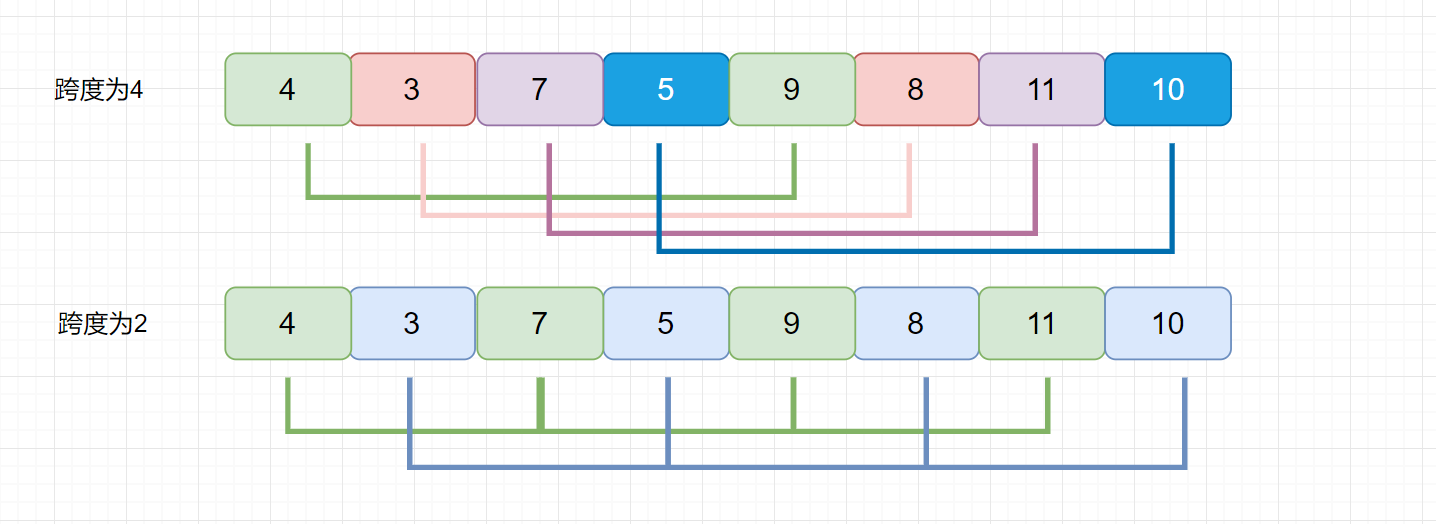
????????我們發現無論是以 4 為增量，還是以 2 為增量，每組內部的元素沒有任何交換。直到增量為 1 時，數組才會按照直接插入排序進行調整。所以這種情況希爾排序的效率是低于直接插入排序呢？

我們的希爾增量因為每一輪之間是等比的，所以會有盲區，這里增量的選取就非常關鍵了。

下面給大家介紹兩個比較有代表性的 Sedgewick 增量和 Hibbard 增量

Sedgewick 增量序列如下：

1，5，19，41，109.。。。

通項公式 94^k - 92^

利用此種增量方式的希爾排序，最壞時間復雜度是O(n^(4/3))

Hibbard增量序列如下：

1，3，7，15......

通項公式2 ^ k-1

利用此種增量方式的希爾排序，最壞時間復雜度為O(n^(3/2))

上面是兩種比較具有代表性的增量方式，可究竟應該選取怎樣的增量才是最好，目前還是一個數學難題。不過我們需要注意的一點，就是增量序列的最后一個增量值必須等于1才行。

希爾排序時間復雜度分析

希爾排序的時間復雜度跟增量序列的選擇有關，范圍為 O(n^(1.3-2)) 在此之前的排序算法時間復雜度基本都是O(n^2),希爾排序是突破這個時間復雜度的第一批算法之一。

希爾排序空間復雜度分析

根據我們的視頻可知希爾排序的空間復雜度為 O(1),

希爾排序的穩定性分析

我們見下圖，一起來分析下希爾排序的穩定性。

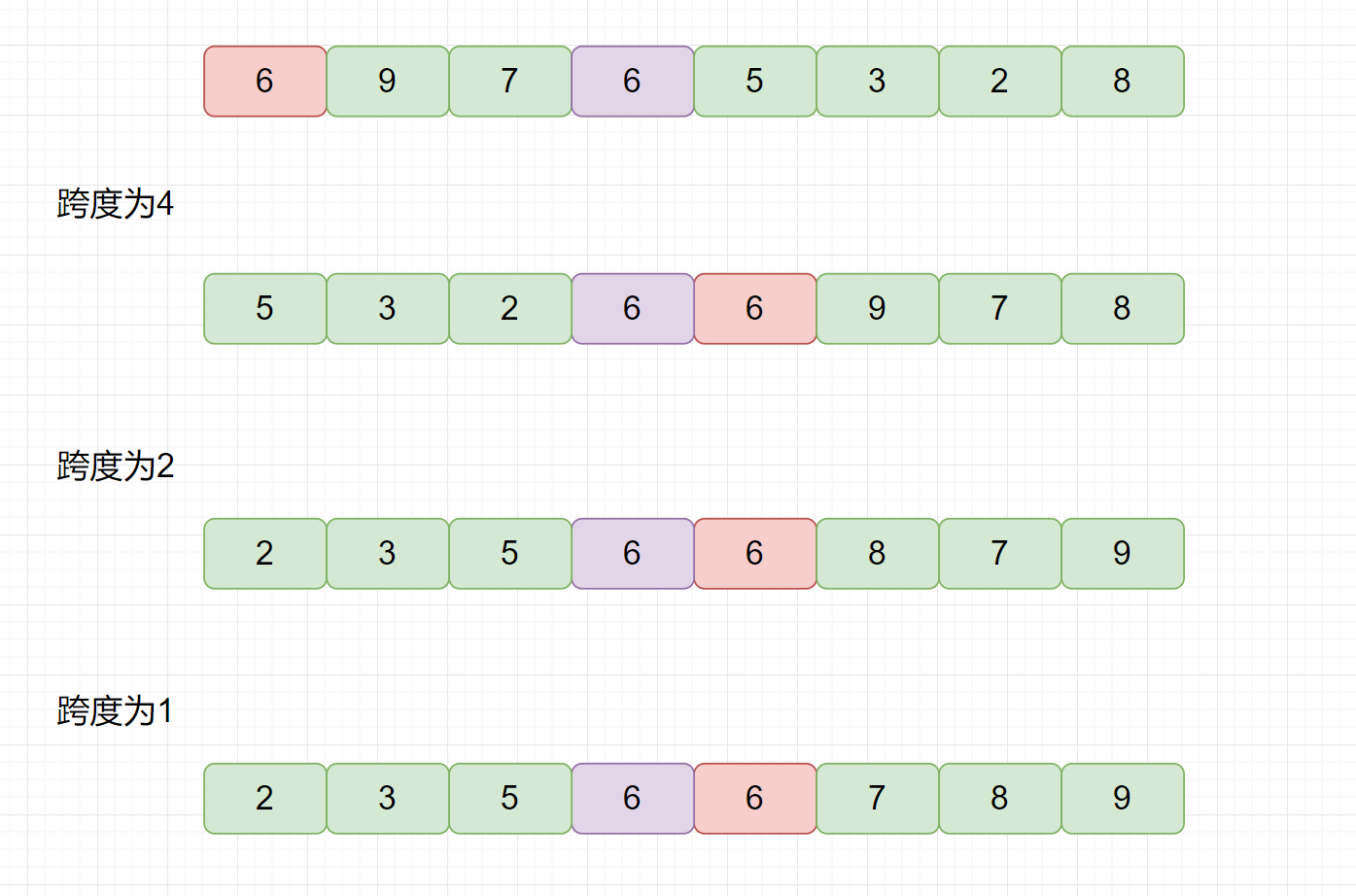
通過上圖，可知，如果我們選用 4 為跨度的話，交換后，兩個相同元素 2 的相對位置會發生改變，所以希爾排序是一個不穩定的排序

---

快速排序

今天我們來說一下快速排序，這個排序算法也是面試的高頻考點，原理很簡單，我們一起來扒一下他吧。

我們先來說一下快速排序的基本思想。

1.先從數組中找一個基準數

2.讓其他比它大的元素移動到數列一邊，比他小的元素移動到數列另一邊，從而把數組拆解成兩個部分。

3.再對左右區間重復第二步，直到各區間只有一個數。

見下圖

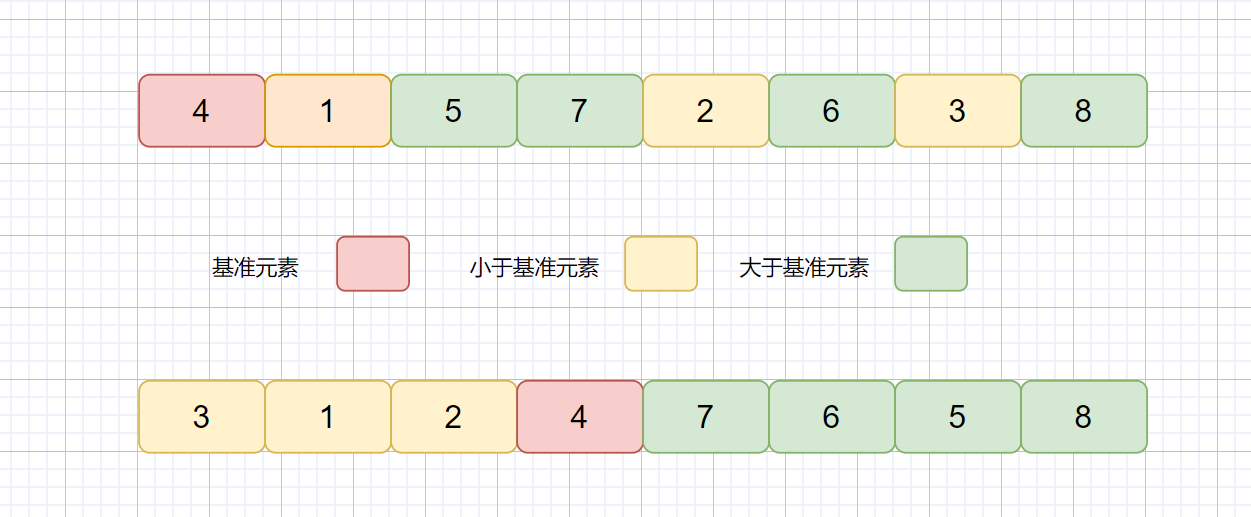
上圖則為一次快排示意圖，下面我們再利用遞歸，分別對左半邊區間也就是 [3,1,2] 和右半區間 [7,6,5,8] 執行上訴過程，直至區間縮小為 1 也就是第三條，則此時所有的數據都有序。

簡單來說就是我們利用基準數通過一趟排序將待排記錄分割成獨立的兩部分，其中一部分記錄的關鍵字均比基準數小，另一部分記錄的關鍵字均比基準數大，然后分別對這兩部分記錄繼續進行排序，進而達到有序。

我們現在應該了解了快速排序的思想，那么大家還記不記得我們之前說過的歸并排序，他們兩個用到的都是分治思想，那他們兩個有什么不同呢？見下圖

注：快速排序我們以序列的第一個元素作為基準數

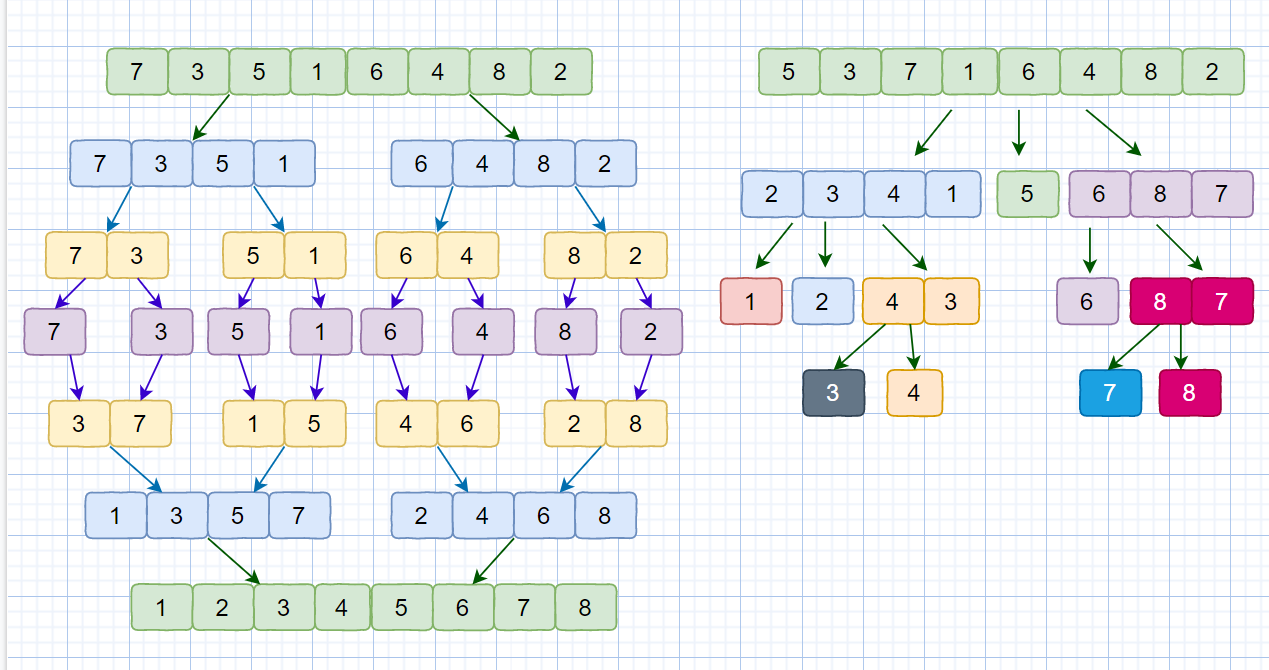
雖然歸并排序和快速排序都用到了分治思想，但是歸并排序是自下而上的，先處理子問題，然后再合并，將小集合合成大集合，最后實現排序。而快速排序是由上到下的，先分區，然后再處理子問題。歸并排序雖然是穩定的、時間復雜度為 O(nlogn) 的排序算法，但是它是非原地排序算法。我們前面講過，歸并之所以是非原地排序算法，主要原因是合并函數無法在原地執行。快速排序通過設計巧妙的原地分區函數，可以實現原地排序，解決了歸并排序占用太多內存的問題

我們根據思想可知，排序算法的核心就是如何利用基準數將記錄分區，這里我們主要介紹兩種容易理解的方法，一種是挖坑填數，另一種是利用雙指針思想進行元素交換。

挖坑填數

下面我們先來介紹下挖坑填數的分區方法

基本思想是我們首先以序列的第一個元素為基準數，然后將該位置挖坑，下面判斷 nums[hight] 是否大于基準數，如果大于則左移 hight 指針，直至找到一個小于基準數的元素，將其填入之前的坑中，則 hight 位置會出現一個新的坑，此時移動 low 指針，找到大于基準數的元素，填入新的坑中。不斷迭代直至完成分區。

大家直接看我們的視頻模擬吧，一目了然。

注：為了便于理解所以采取了挖坑的形式展示

是不是很容易就理解啦，下面我們直接看代碼吧。

class Solution {public int[] sortArray(int[] nums) { quickSort(nums,0,nums.length-1);return nums;}public void quickSort (int[] nums, int low, int hight) {if (low < hight) {int index = partition(nums,low,hight);quickSort(nums,low,index-1);quickSort(nums,index+1,hight);}    }public int partition (int[] nums, int low, int hight) {int pivot = nums[low];while (low < hight) {//移動hight指針while (low < hight && nums[hight] >= pivot) {hight--;}//填坑if (low < hight) nums[low] = nums[hight];while (low < hight && nums[low] <= pivot) {low++;}//填坑if (low < hight) nums[hight] = nums[low];}//基準數放到合適的位置nums[low] = pivot;return low;}   
}

交換位置

下面我們來看一下交換思路，原理一致，實現也比較簡單。

見下圖。

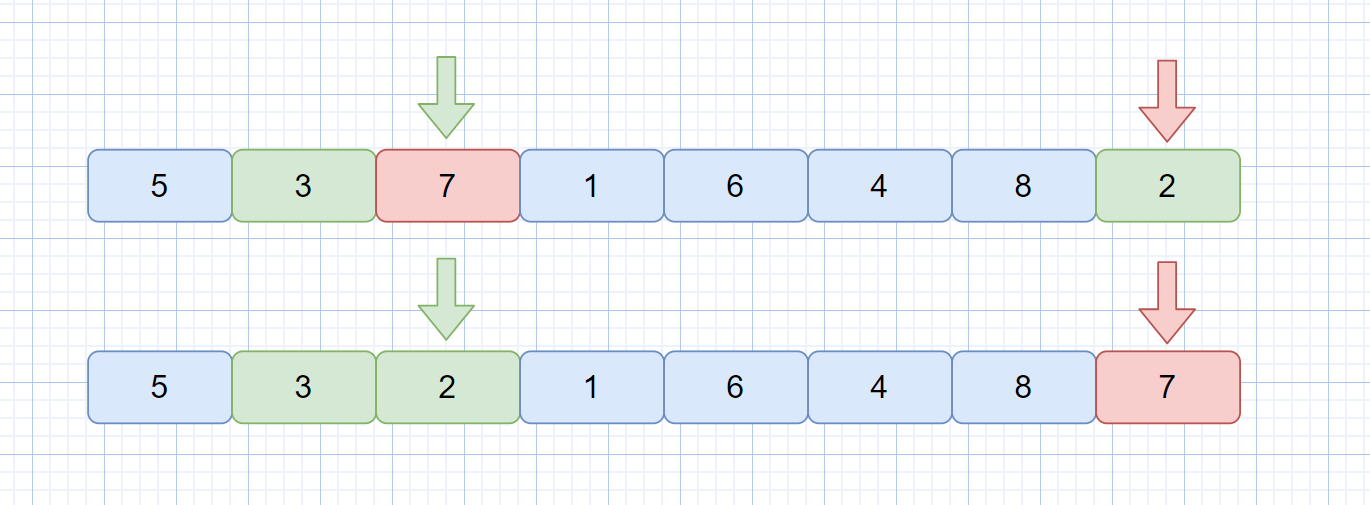
其實這種方法，算是對上面方法的挖坑填坑步驟進行合并，low 指針找到大于 pivot 的元素，hight 指針找到小于 pivot 的元素，然后兩個元素交換位置，最后再將基準數歸位。兩種方法都很容易理解和實現，即使是完全沒有學習過快速排序的同學，理解了思想之后也能自己動手實現，下面我們繼續用視頻模擬下這種方法的執行過程吧。

兩種方法都很容易實現，對新手非常友好，大家可以自己去 AC 一下啊。

class Solution {public int[] sortArray (int[] nums) {   quickSort(nums,0,nums.length-1);return nums;}public void quickSort (int[] nums, int low, int hight) {if (low < hight) {int index = partition(nums,low,hight);quickSort(nums,low,index-1);quickSort(nums,index+1,hight);} }public int partition (int[] nums, int low, int hight) {int pivot = nums[low];int start = low;while (low < hight) {while (low < hight && nums[hight] >= pivot) hight--;           while (low < hight && nums[low] <= pivot) low++;if (low >= hight) break;swap(nums, low, hight);  }//基準值歸位swap(nums,start,low);return low;}  public void swap (int[] nums, int i, int j) {      int temp = nums[i];nums[i] = nums[j];nums[j] = temp;} 
}

快速排序的時間復雜度分析

快排也是用遞歸來實現的。所以快速排序的時間性能取決于快速排序的遞歸樹的深度。如果每次分區操作，都能正好把數組分成大小接近相等的兩個小區間，那么此時的遞歸樹是平衡的，性能也較好，遞歸樹的深度也就和之前歸并排序求解方法一致，然后我們每一次分區需要對數組掃描一遍，做 n 次比較，所以最優情況下，快排的時間復雜度是 O(nlogn)。

但是大多數情況下我們不能劃分的很均勻，比如數組為正序或者逆序時，即 [1,2,3,4] 或 [4,3,2,1] 時，此時為最壞情況，那么此時我們則需要遞歸調用 n-1 次，此時的時間復雜度則退化到了 O(n^2)。

快速排序的空間復雜度分析

快速排序主要時遞歸造成的棧空間的使用，最好情況時其空間復雜度為O (logn),對應遞歸樹的深度。最壞情況時則需要 n-1 次遞歸調用，此時空間復雜度為O(n).

快速排序的穩定性分析

快速排序是一種不穩定的排序算法，因為其關鍵字的比較和交換是跳躍進行的，見下圖。

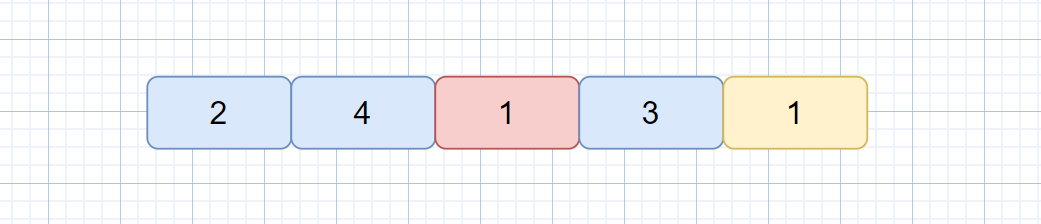
此時無論使用哪一種方法，第一次排序后，黃色的 1 都會跑到紅色 1 的前面，所以快速排序是不穩定的排序算法。

好啦，快速排序我們掌握的差不多了，下面我們一起來看看如何對其優化吧。

快速排序的迭代寫法

該方法實現也是比較簡單的，借助了棧來實現，很容易實現。主要利用了先進后出的特性，這里需要注意的就是入棧的順序，這里算是一個小細節，需要注意一下。

class Solution {public int[] sortArray(int[] nums) {Stack<Integer> stack = new Stack<>();stack.push(nums.length - 1);stack.push(0);while (!stack.isEmpty()) {int low = stack.pop();int hight = stack.pop();if (low < hight) {int index = partition(nums, low, hight);stack.push(index - 1);stack.push(low);stack.push(hight);stack.push(index + 1);}}return nums;}public int partition (int[] nums, int low, int hight) {int pivot = nums[low];int start = low;while (low < hight) {while (low < hight && nums[hight] >= pivot) hight--;           while (low < hight && nums[low] <= pivot) low++;if (low >= hight) break;swap(nums, low, hight); }swap(nums,start,low);return low;} public void swap (int[] nums, int i, int j) {    int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}  
}

快速排序優化

三數取中法

我們在上面的例子中選取的都是 nums[low] 做為我們的基準值，那么當我們遇到特殊情況時呢？見下圖

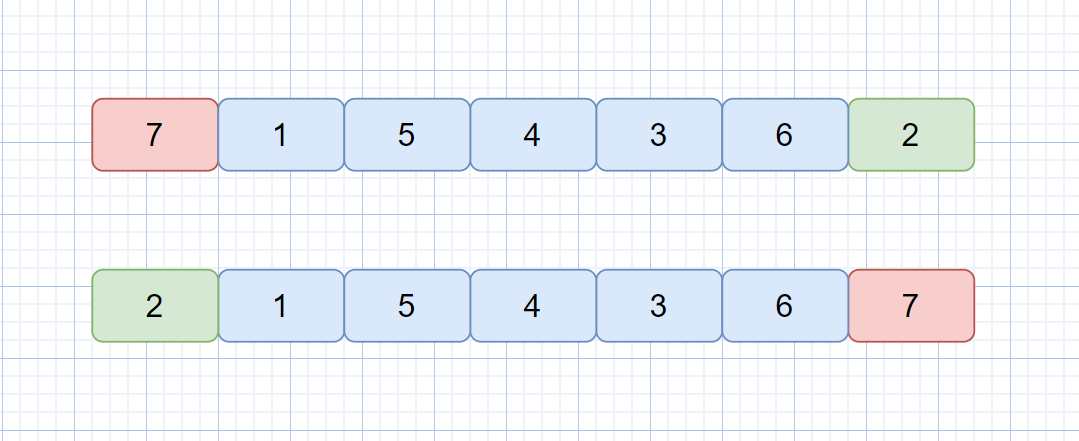
我們按上面的方法，選取第一個元素做為基準元素，那么我們執行一輪排序后，發現僅僅是交換了 2 和 7 的位置，這是因為 7 為序列的最大值。所以我們的 pivot 的選取尤為重要，選取時應盡量避免選取序列的最大或最小值做為基準值。則我們可以利用三數取中法來選取基準值。

也就是選取三個元素中的中間值放到 nums[low] 的位置，做為基準值。這樣就避免了使用最大值或最小值做為基準值。

所以我們可以加上這幾行代碼實現三數取中法。

     int mid = low + ((hight-low) >> 1);if (nums[low] > nums[hight]) swap(nums,low,hight);if (nums[mid] > nums[hight]) swap(nums,mid,hight);if (nums[mid] > nums[low]) swap(nums,mid,low); 

其含義就是讓我們將中間元素放到 nums[low] 位置做為基準值，最大值放到 nums[hight],最小值放到 nums[mid],即 [4,2,3] 經過上面代碼處理后，則變成了 [3,2,4].此時我們選取 3 做為基準值，這樣也就避免掉了選取最大或最小值做為基準值的情況。

三數取中法

class Solution {public int[] sortArray(int[] nums) {       quickSort(nums,0,nums.length-1);return nums;}public void quickSort (int[] nums, int low, int hight) {if (low < hight) {int index = partition(nums,low,hight);quickSort(nums,low,index-1);quickSort(nums,index+1,hight);}       }public int partition (int[] nums, int low, int hight) {//三數取中，大家也可以使用其他方法int mid = low + ((hight-low) >> 1);if (nums[low] > nums[hight]) swap(nums,low,hight);if (nums[mid] > nums[hight]) swap(nums,mid,hight);if (nums[mid] > nums[low]) swap(nums,mid,low); //下面和之前一樣，僅僅是多了上面幾行代碼int pivot = nums[low];int start = low;while (low < hight) {while (low < hight && nums[hight] >= pivot) hight--;           while (low < hight && nums[low] <= pivot) low++;if (low >= hight) break;swap(nums, low, hight); }swap(nums,start,low);return low;}  public void swap (int[] nums, int i, int j) {     int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}  
}

和插入排序搭配使用

我們之前說過，插入排序在元素個數較少時效率是最高的，所以當元素數量較少時，快速排序反而不如插入排序好用，所以我們可以設定一個閾值，當元素個數大于閾值時使用快速排序，小于等于該閾值時則使用插入排序。我們設定閾值為 7 。

三數取中+插入排序

class Solution {private static final int INSERTION_SORT_MAX_LENGTH = 7;public int[] sortArray(int[] nums) {      quickSort(nums,0,nums.length-1);return nums;}public void quickSort (int[] nums, int low, int hight) {if (hight - low <= INSERTION_SORT_MAX_LENGTH) {insertSort(nums,low,hight);return;}               int index = partition(nums,low,hight);quickSort(nums,low,index-1);quickSort(nums,index+1,hight);         }public int partition (int[] nums, int low, int hight) {//三數取中，大家也可以使用其他方法int mid = low + ((hight-low) >> 1);if (nums[low] > nums[hight]) swap(nums,low,hight);if (nums[mid] > nums[hight]) swap(nums,mid,hight);if (nums[mid] > nums[low]) swap(nums,mid,low);   int pivot = nums[low];int start = low;while (low < hight) {while (low < hight && nums[hight] >= pivot) hight--;           while (low < hight && nums[low] <= pivot) low++;if (low >= hight) break;swap(nums, low, hight); }swap(nums,start,low);return low;} public void insertSort (int[] nums, int low, int hight) {for (int i = low+1; i <= hight; ++i) {int temp = nums[i];int j;for (j = i-1; j >= 0; --j) {if (temp < nums[j]) {nums[j+1] = nums[j];continue;} break;}nums[j+1] = temp;}} public void swap (int[] nums, int i, int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;} 
}

三數取中+三向切分+插入排序

我們繼續看下面這種情況

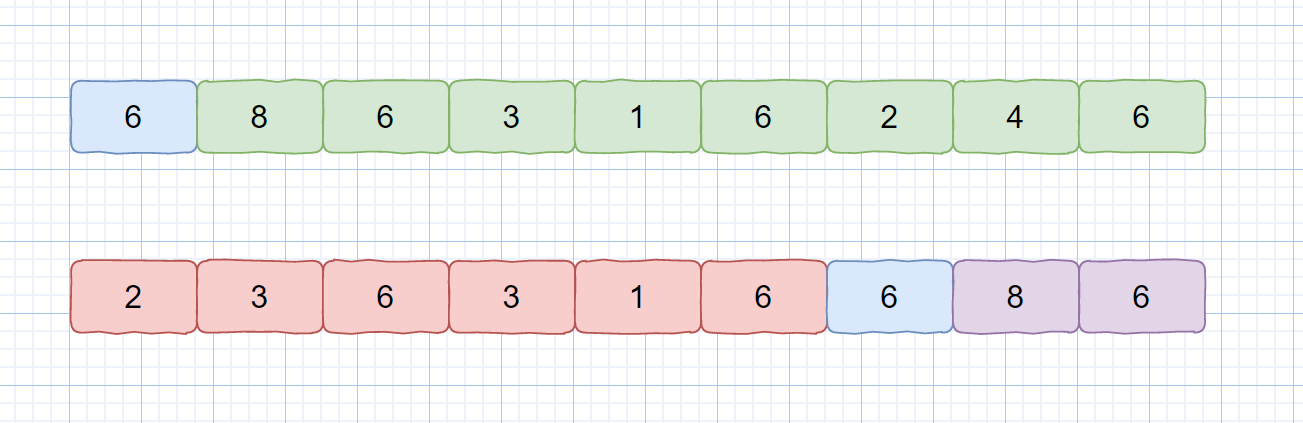
我們對其執行一次排序后，則會變成上面這種情況，然后我們繼續對藍色基準值的左區間和右區間執行相同操作。也就是 [2,3,6,3,1,6] 和 [8,6] 。我們注意觀察一次排序的結果數組中是含有很多重復元素的。

那么我們為什么不能將相同元素放到一起呢？這樣就能大大減小遞歸調用時的區間大小，見下圖。

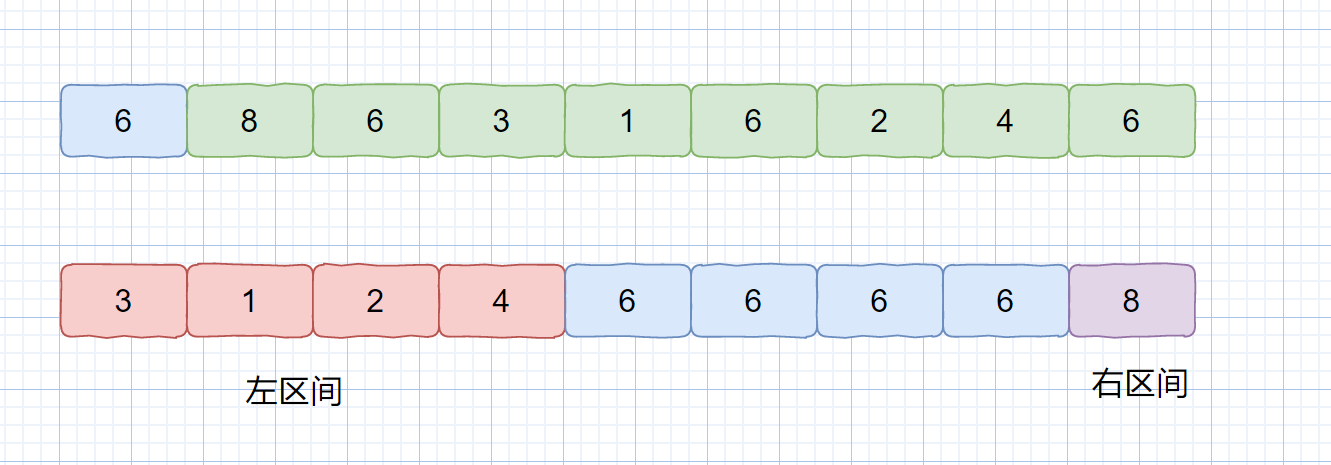
這樣就減小了我們的區間大小，將數組切分成了三部分，小于基準數的左區間，大于基準數的右區間，等于基準數的中間區間。

下面我們來看一下如何達到上面的情況，我們先來進行視頻模擬，模擬之后應該就能明白啦。

我們來剖析一下視頻，其實原理很簡單，我們利用探路指針也就是 i，遇到比 pivot 大的元素，則和 right 指針進行交換，此時 right 指向的元素肯定比 pivot 大，則 right--，但是，此時我們的 nums[i] 指向的元素并不知道情況，所以我們的 i 指針不動，如果此時 nums[i] < pivot 則與 left 指針交換，注意此時我們的 left 指向的值肯定是 等于 povit的，所以交換后我們要 left++,i++, nums[i] == pivot 時，僅需要 i++ 即可，繼續判斷下一個元素。 我們也可以借助這個思想來解決經典的荷蘭國旗問題。

好啦，我們下面直接看代碼吧。

class Solution {private static final int INSERTION_SORT_MAX_LENGTH = 7;public int[] sortArray(int[] nums) {quickSort(nums,0,nums.length-1);return nums;}public void quickSort(int nums[], int low, int hight) {//插入排序if (hight - low <= INSERTION_SORT_MAX_LENGTH) {insertSort(nums,low,hight);return;}//三數取中int mid = low + ((hight-low) >> 1);if (nums[low] > nums[hight]) swap(nums,low,hight);if (nums[mid] > nums[hight]) swap(nums,mid,hight);if (nums[mid] > nums[low]) swap(nums,mid,low);//三向切分int left = low,  i = low + 1, right = hight;int pvoit = nums[low];while (i <= right) {if (pvoit < nums[i]) {swap(nums,i,right);right--;} else if (pvoit == nums[i]) {i++;} else {swap(nums,left,i);left++;i++;}}quickSort(nums,low,left-1);quickSort(nums,right+1,hight);}public void insertSort (int[] nums, int low, int hight) {for (int i = low+1; i <= hight; ++i) {int temp = nums[i];int j;for (j = i-1; j >= 0; --j) {if (temp < nums[j]) {nums[j+1] = nums[j];continue;} break;}nums[j+1] = temp;}} public  void swap (int[] nums, int i, int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}
}

好啦，一些常用的優化方法都整理出來啦，還有一些其他的優化算法九數取中，優化遞歸操作等就不在這里進行描述啦，感興趣的可以自己看一下。好啦，這期的文章就到這里啦，我們下期見，拜了個拜。

---

堆排序

說堆排序之前，我們先簡單了解一些什么是堆？堆這種數據結構應用場景非常多，所以我們需要熟練掌握呀！

那我們了解堆之前，先來簡單了解下，什么是完全二叉樹？

我們來看下百度百科的定義，完全二叉樹：葉子結點只能出現在最下層和次下層，且最下層的葉子結點集中在樹的左部。

哦！我們可以這樣理解，除了最后一層，其他層的節點個數都是滿的，而且最后一層的葉子節點必須靠左。

下面我們來看一下這幾個例子

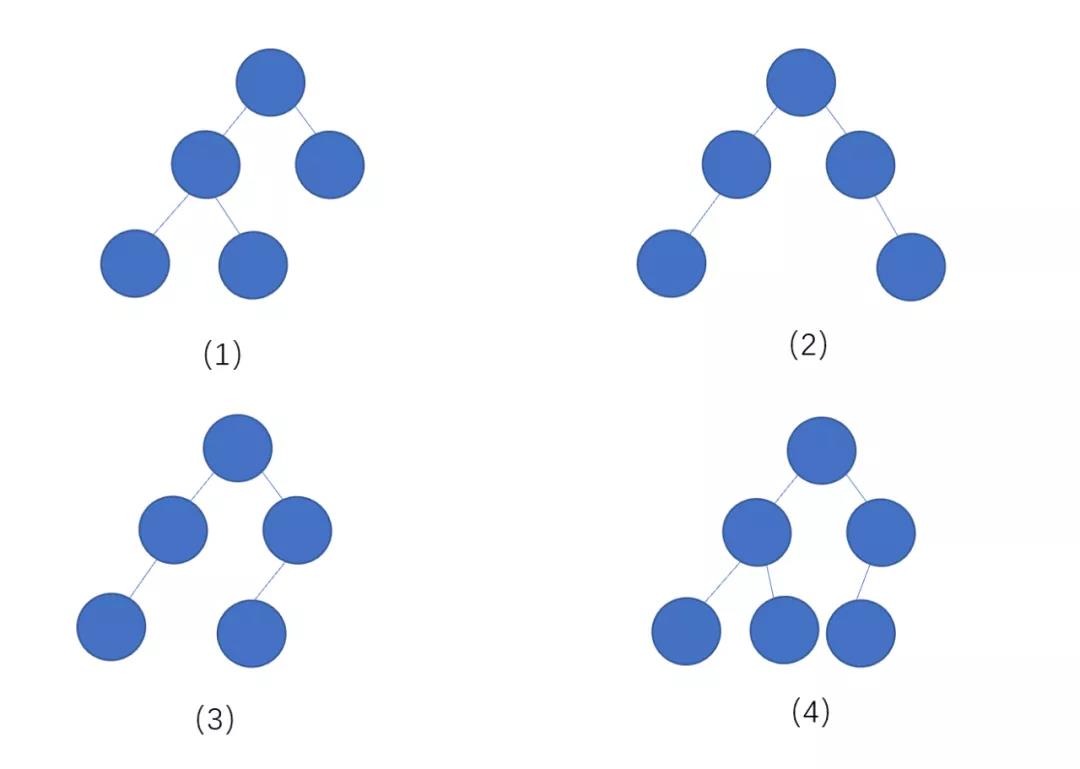
上面的幾個例子中，（1）（4）為完全二叉樹，（2）（3）不是完全二叉樹，通過上面的幾個例子，我們了解了什么是完全二叉樹，

那么堆到底是什么呢？

下面我們來看一下二叉堆的要求

（1）必須是完全二叉樹

（2）二叉堆中的每一個節點，都必須大于等于（或小于等于）其子樹中每個節點的值。

若是每個節點大于等于子樹中的每個節點，我們稱之為大頂堆，小于等于子樹中的每個節點，我們則稱之為小頂堆。見下圖

下面我們再來看一下二叉堆的具體例子。

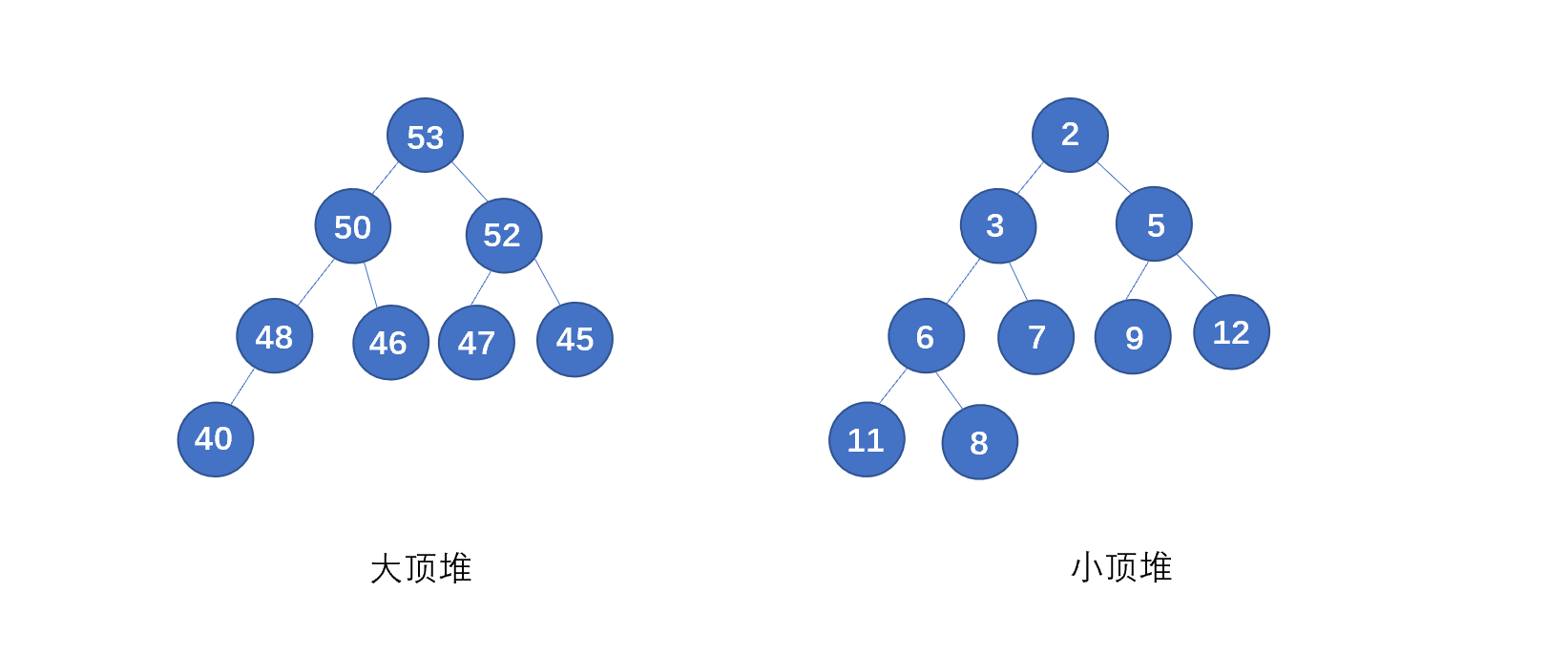
上圖則為大頂堆和小頂堆，我們再來回顧一下堆的要求，看下是否符合

（1）必須是完全二叉樹

（2）堆中的每一個節點，都必須大于等于（或小于等于）其子樹中每個節點的值。

好啦，到這里我們已經完全掌握二叉堆了，那么二叉堆又是怎么存儲的呢？因為堆是完全二叉樹，所以我們完全可以用數組存儲。具體思想見下圖，我們僅僅按照順序將節點存入數組即可，我們通過小頂堆進行演示。

注：我們是從下標 1 開始存儲的，這樣能省略一些計算，下文中我們將二叉堆簡稱為堆

我們來看一下為什么我們可以用數組來存儲堆呢？

我們首先看根節點，也就是值為 1 的節點，它在數組中的下標為 1 ,它的左子節點，也就是值為 4 的節點，此時索引為 2，右子節點也就是值為 2 的節點，它的索引為 3。

我們發現其中的關系了嗎？

數組中，某節點（非葉子節點）的下標為 i , 那么其左子節點下標為 2*i?（這里可以直接通過相乘得到左孩子，如果從0 開始存，需要 2i+1 才行）, 右子節點為 2i+1，其父節點為 i/2 。既然我們完全可以根據索引找到某節點的?左子節點?和?右子節點，那么我們用數組存儲是完全沒有問題的。

好啦，我們知道了什么是堆和如何用數組存儲堆，那我們如何完成堆排序呢？

堆排序其實主要有兩個步驟

• 建堆
• 排序

下面我們先來了解下建堆

我們剛才說了用數組來存儲大頂（小頂）堆，此時的元素已經滿足某節點大于等于（或小于等于）子樹節點，但是隨機給我們一個數組，此時并不一定滿足上訴要求，所以我們需要調整數組，使其滿足大頂堆或小頂堆的要求。這個就是堆化，也可以稱其為建堆。

建堆我們這里提出兩種方法，利用上浮操作，也就是不斷插入元素進行建堆，另一種是利用下沉操作，遍歷父節點，不斷將其下沉，進行建堆，我們一起來看吧。

我們先來說下第一種建堆方式

利用上浮操作建堆

說之前我們先來了解下，如何往已經建好的堆里，插入新的元素，我們直接看例子吧，一下就懂啦。

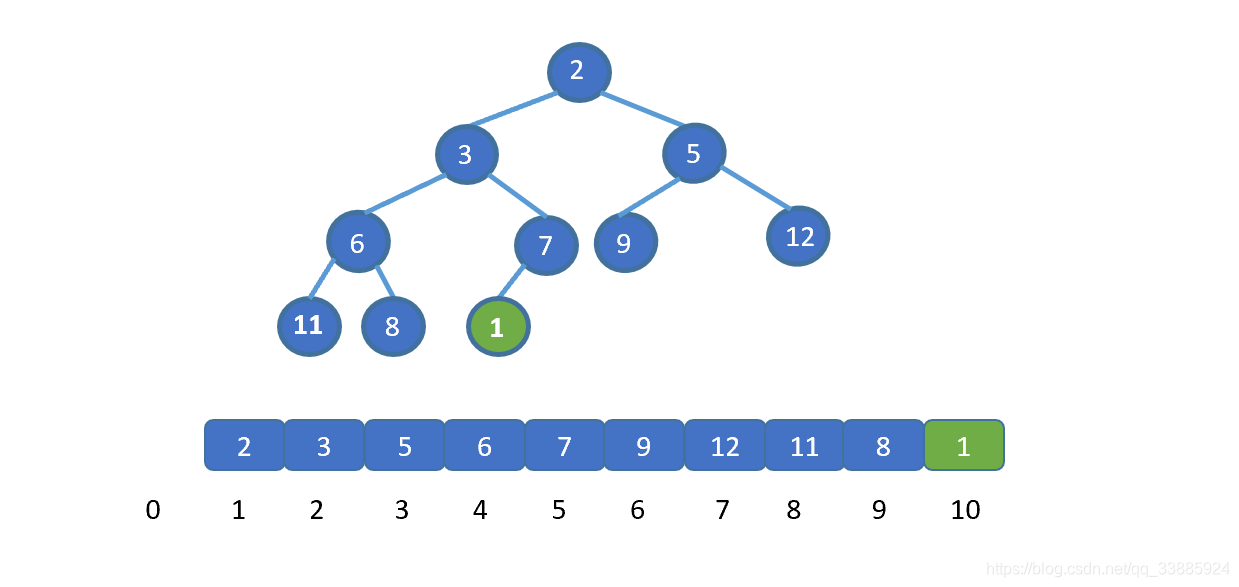
假設讓我們插入新的元素 1 （綠色節點），我們發現此時 1 小于其父節點 的值 7 ，并不遵守小頂堆的規則，那我們則需要移動元素 1 。讓 1 與 7 交換，（如果新插入元素大于父節點的值，則說明插入新節點后仍滿足小頂堆規則，無需交換）。

之前我們說過，我們可以用數組保存堆，并且可以通過 i/2 得到其父節點的值，那么此時我們就明白怎么做啦。

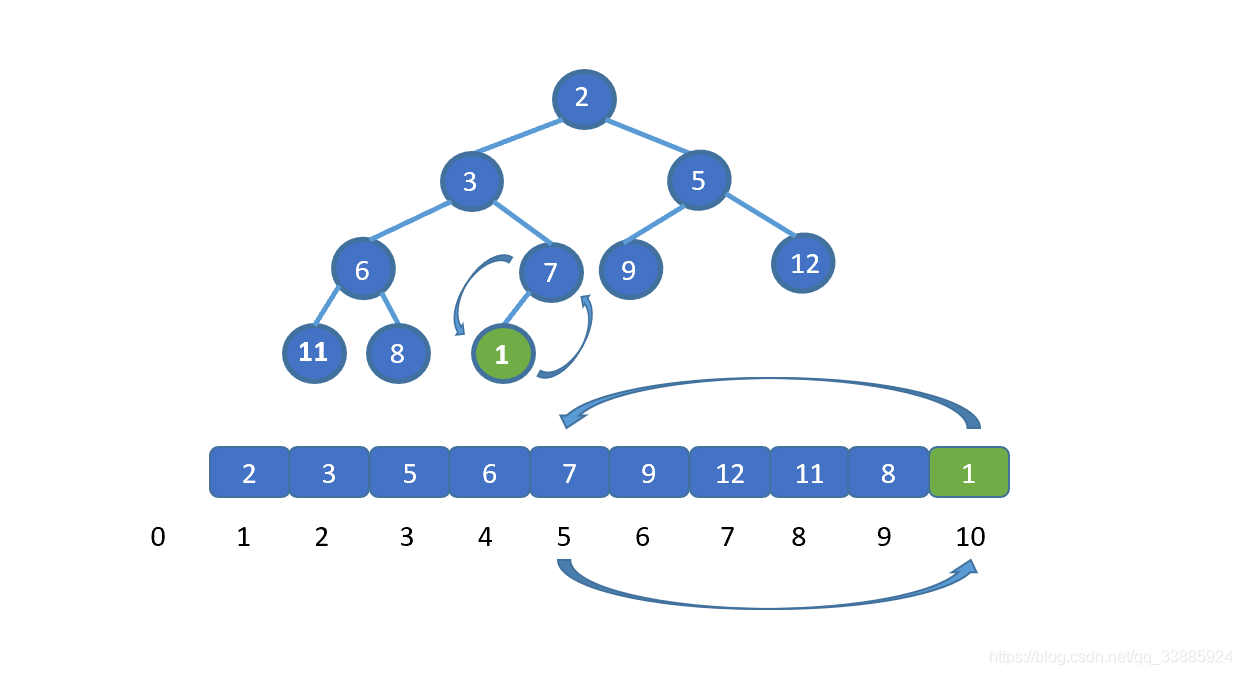
將插入節點與其父節點，交換。

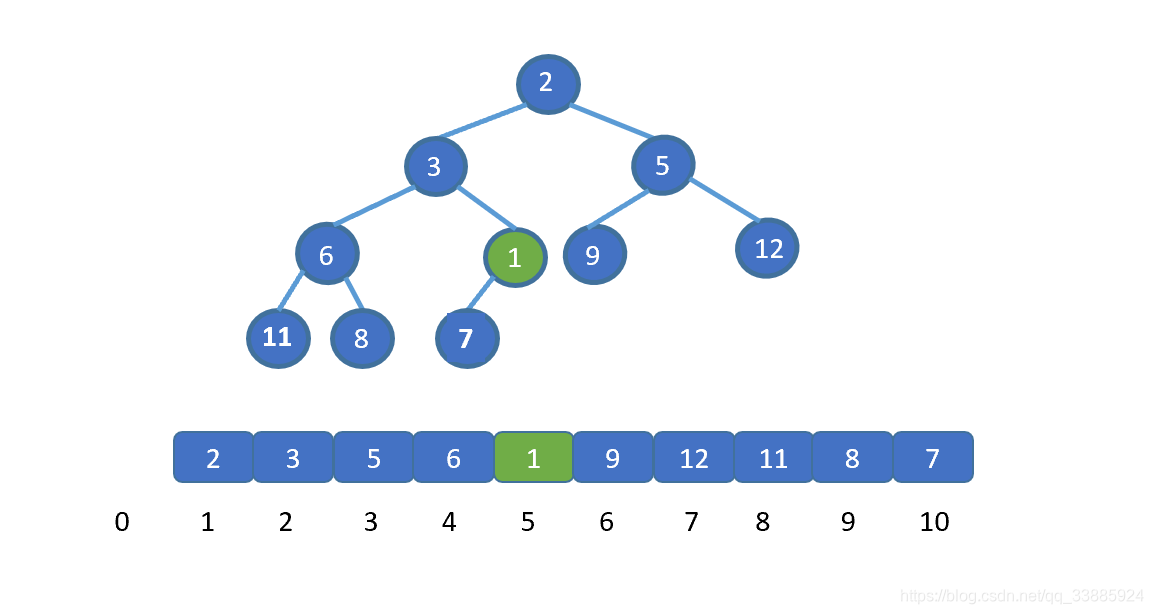
交換之后，我們繼續將新插入元素，也就是 1 與其父節點比較，如果大于其父節點，則無需交換，循環結束。若小于則需要繼續交換，直到 1 到達適合他的地方。大家是不是已經直到該怎么做啦！下面我們直接看動圖吧。

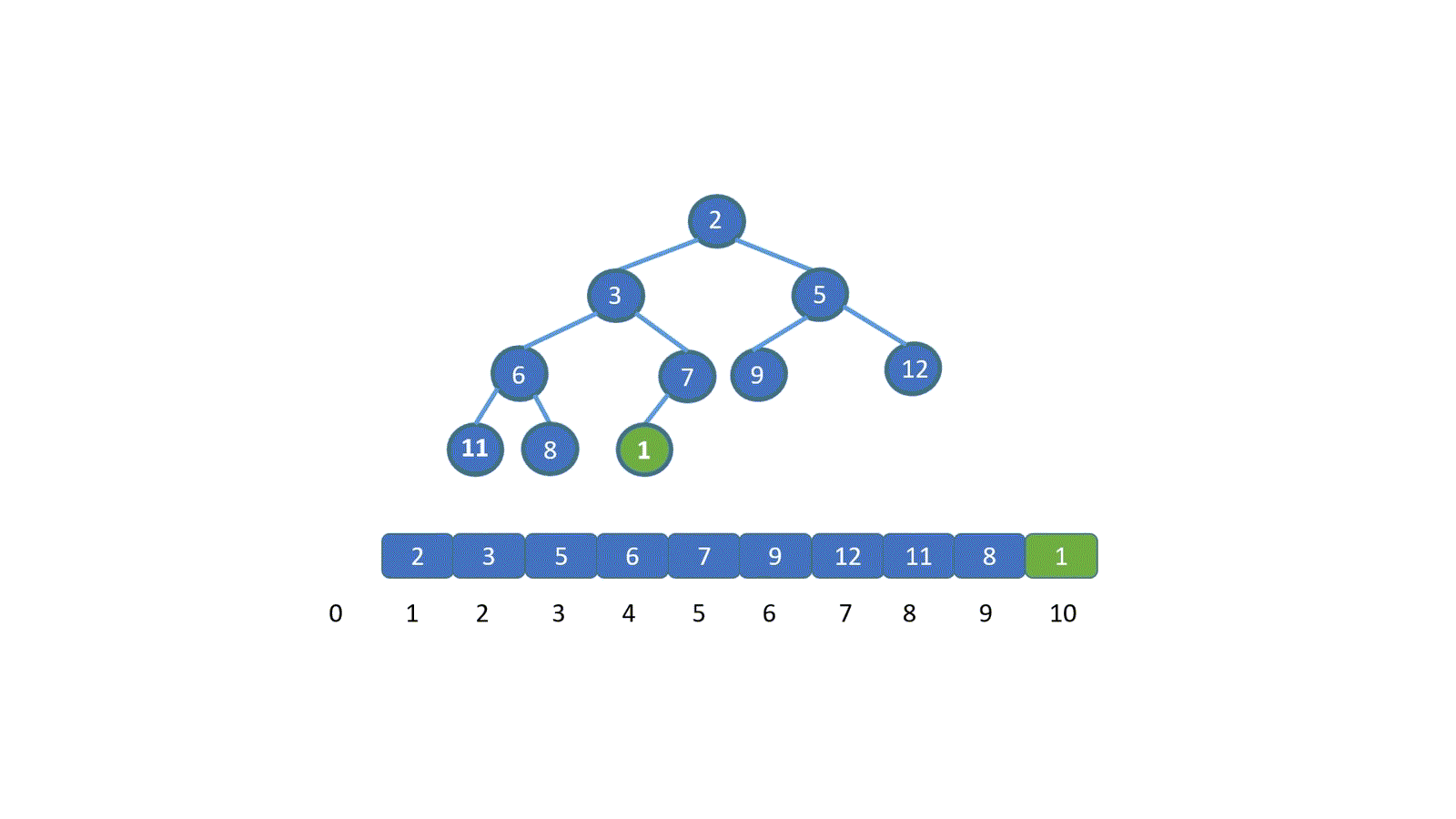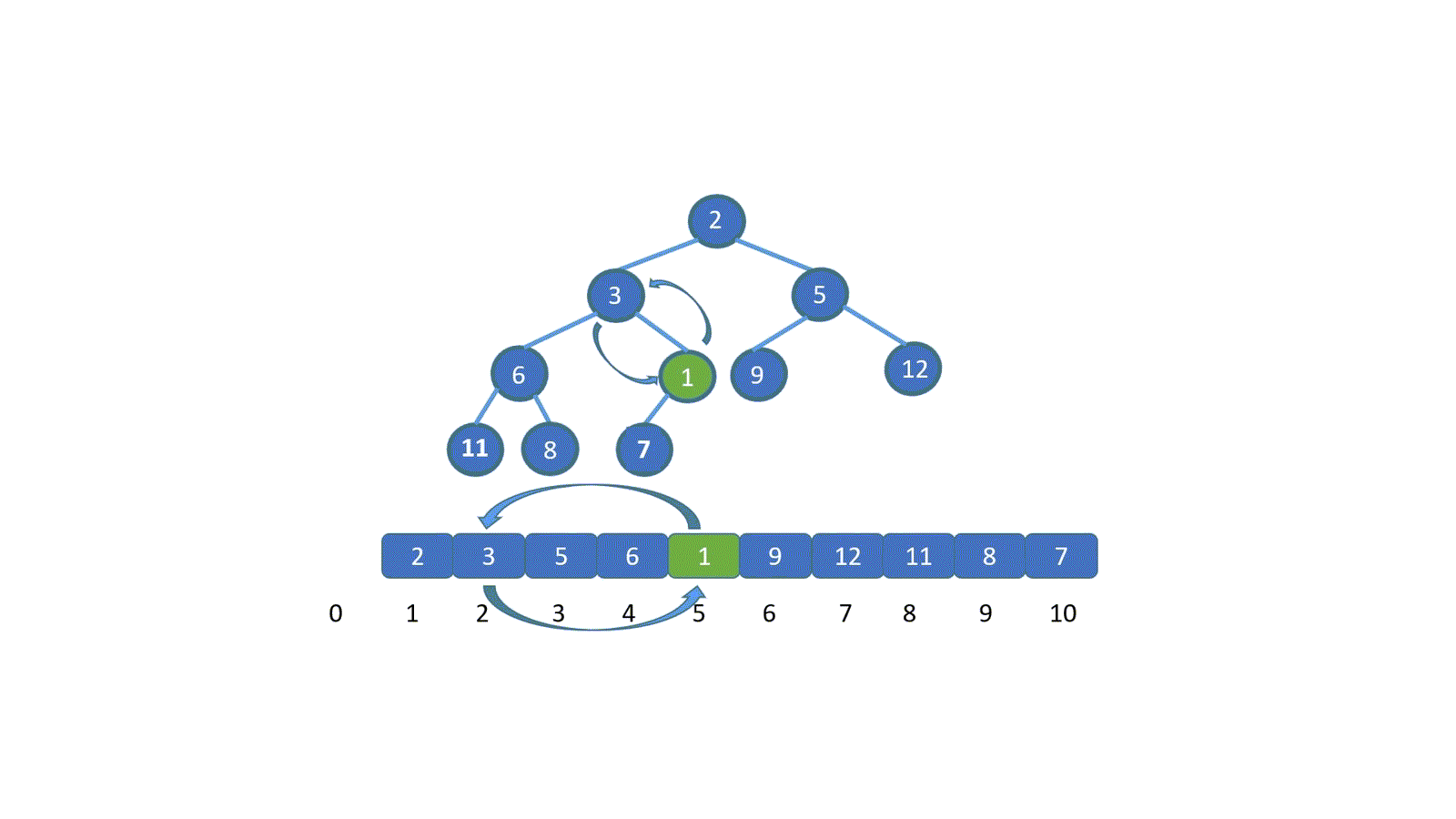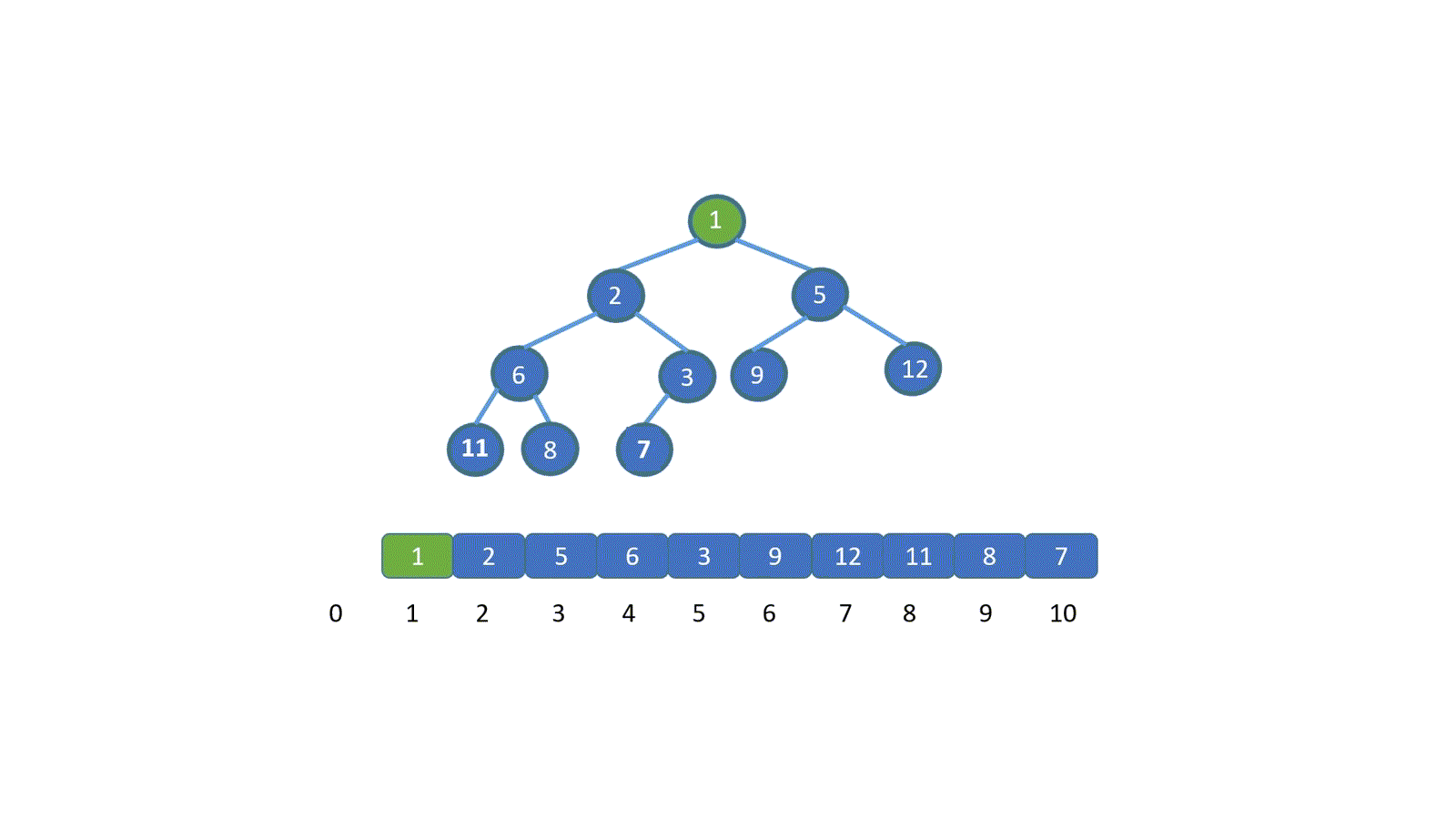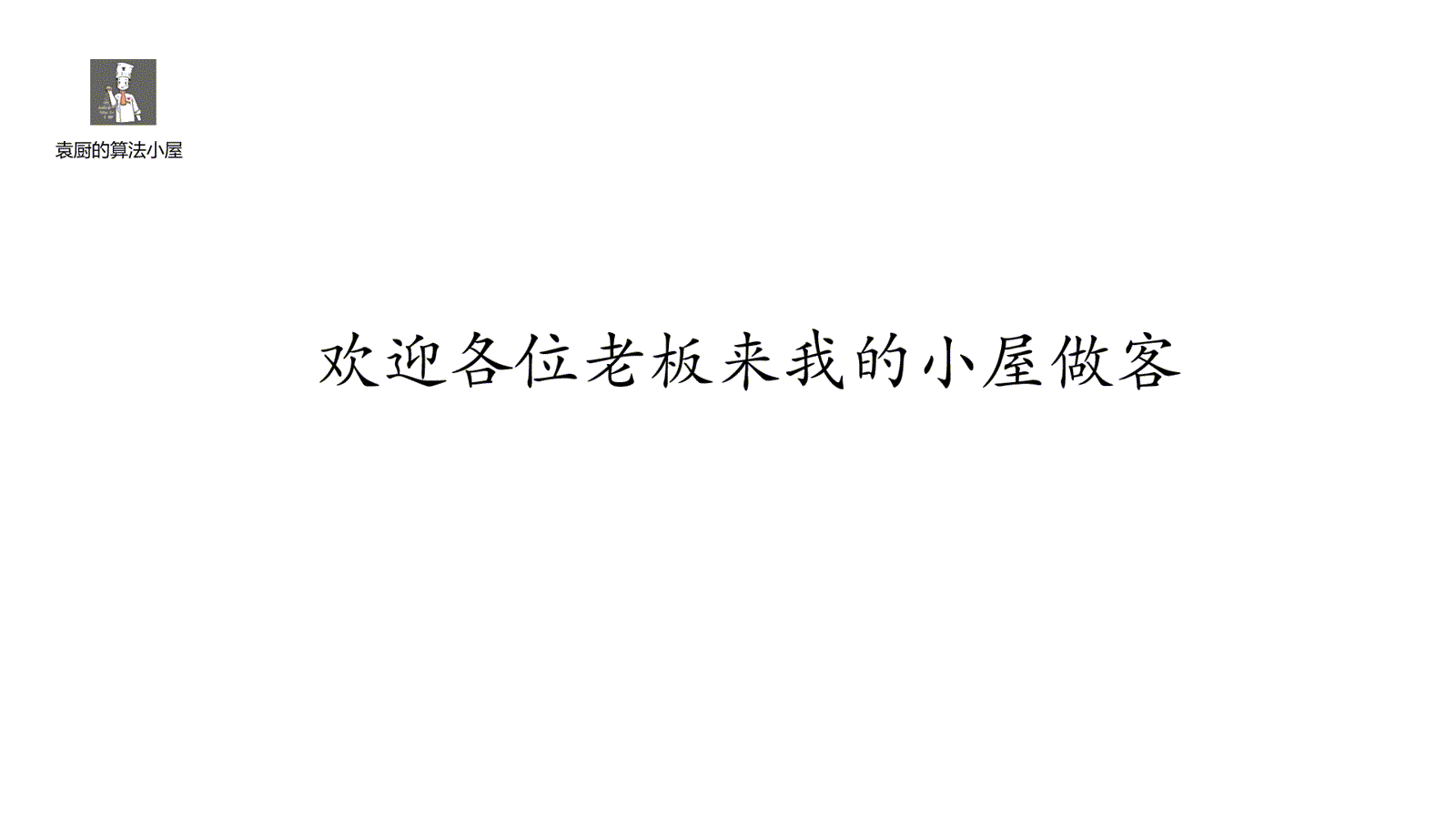
看完動圖是不是就妥了，其實很簡單，我們只需將新加入元素與其父節點比較，判斷是否小于堆頂元素（小頂堆），如果小于則進行交換，（讓更小的節點為父節點）直到符合堆的規則位置，大頂堆則相反。

我們發現，我們新插入的元素是不是一層層的上浮，直到找到屬于自己的位置，我們將這個操作稱之為上浮操作。

那我們知道了上浮，豈不是就可以實現建堆了？是的，我們則可以依次遍歷數組，就好比不斷往堆中插入新元素，直至遍歷結束，這樣我們就完成了建堆，這種方法當然是可以的。

我們一起來看一下上浮操作代碼。

public void swim (int index) {while (index > 1 && nums[index/2] > nums[index]) {swap(index/2,index);//交換index = index/2;}
}

既然利用上浮操作建堆已經搞懂啦，那么我們再來了解一下，利用下沉操作建堆吧，也很容易理解。

下沉建堆

給我們一個無序數組（不滿足堆的要求），見下圖

我們發現，7 位于堆頂，但是此時并不滿足小頂堆的要求，我們需要把 7 放到屬于它的位置，我們應該怎么做呢？

廢話不多說，我們先來看視頻模擬，看完保準可以懂

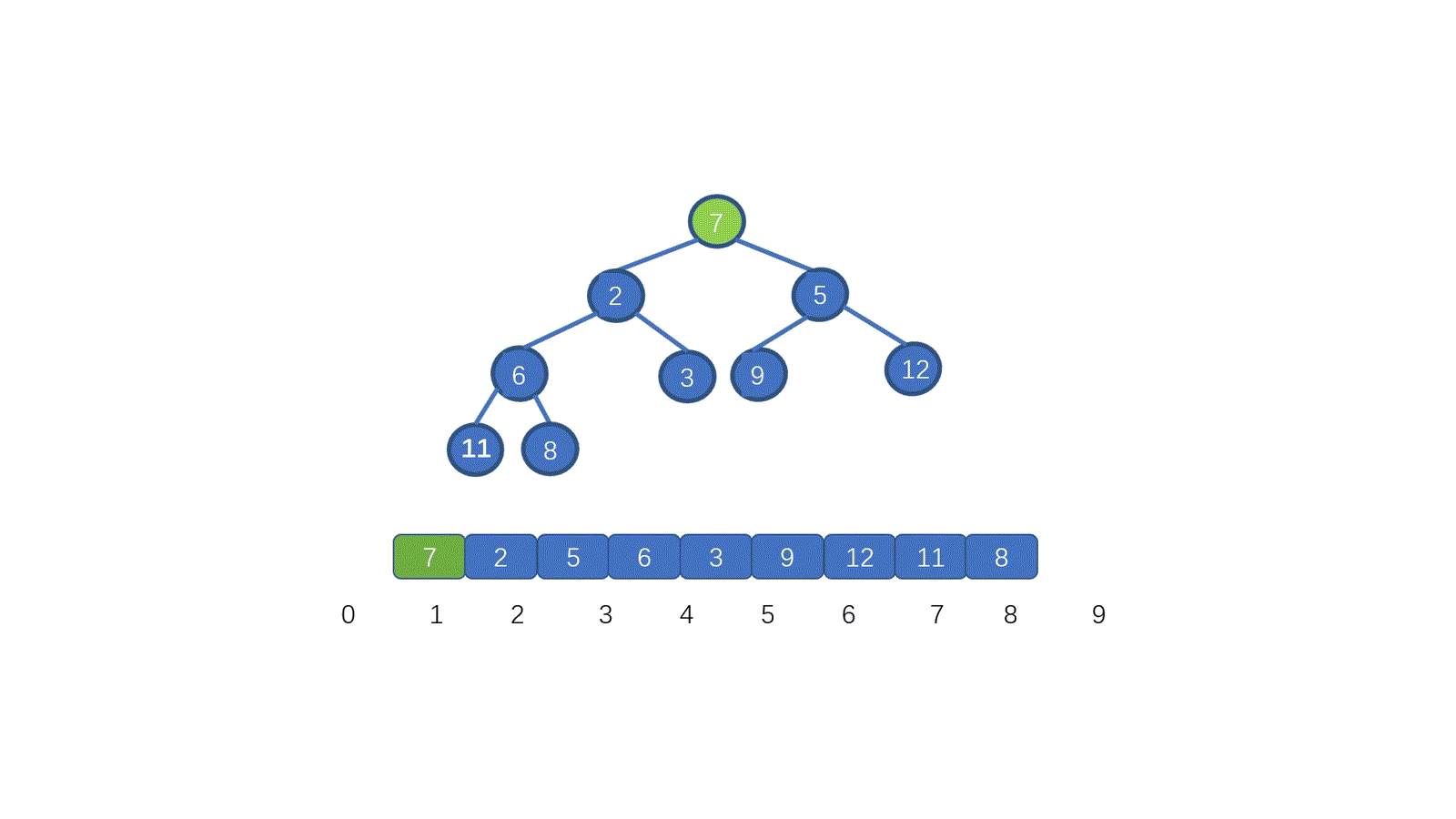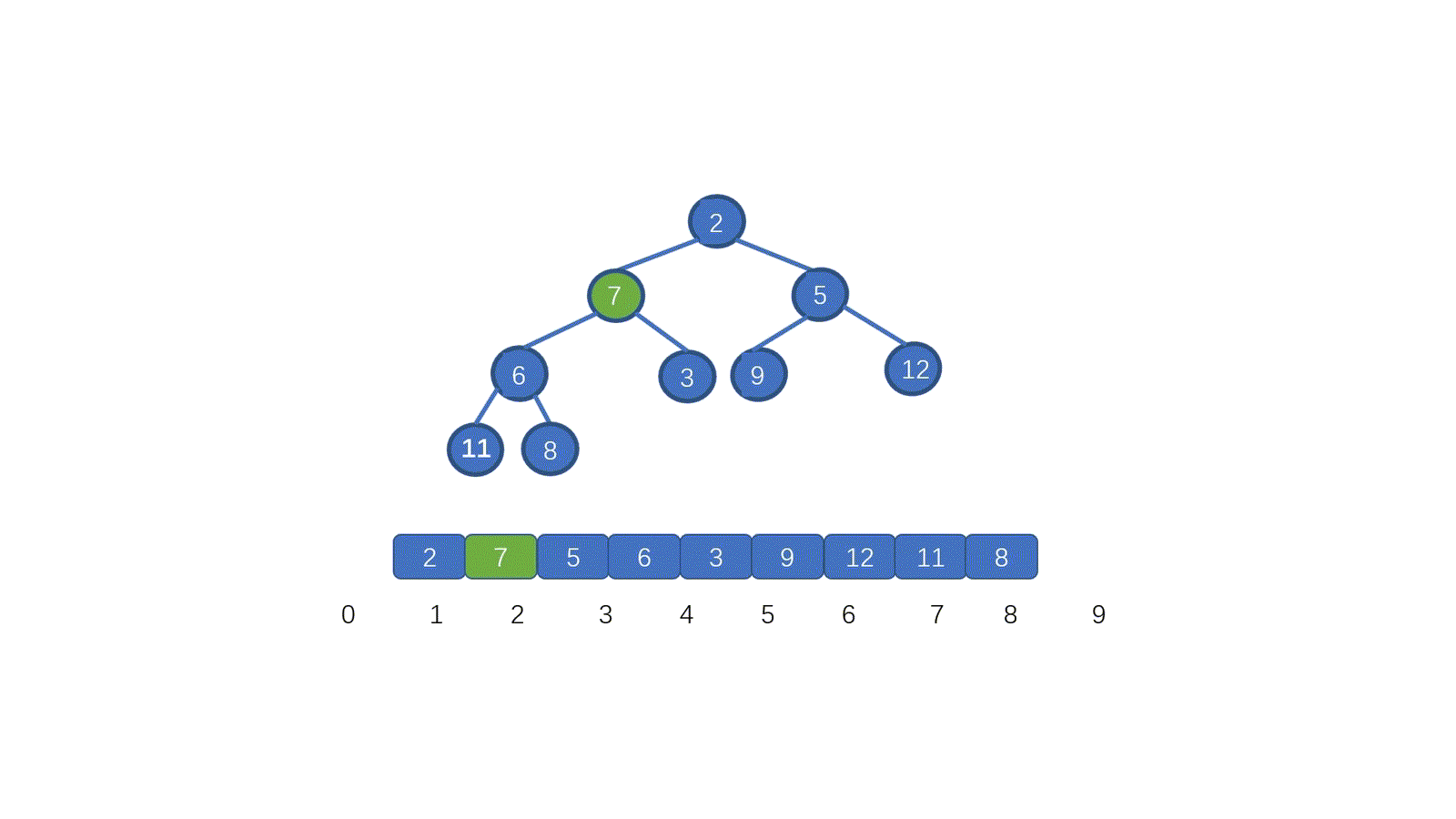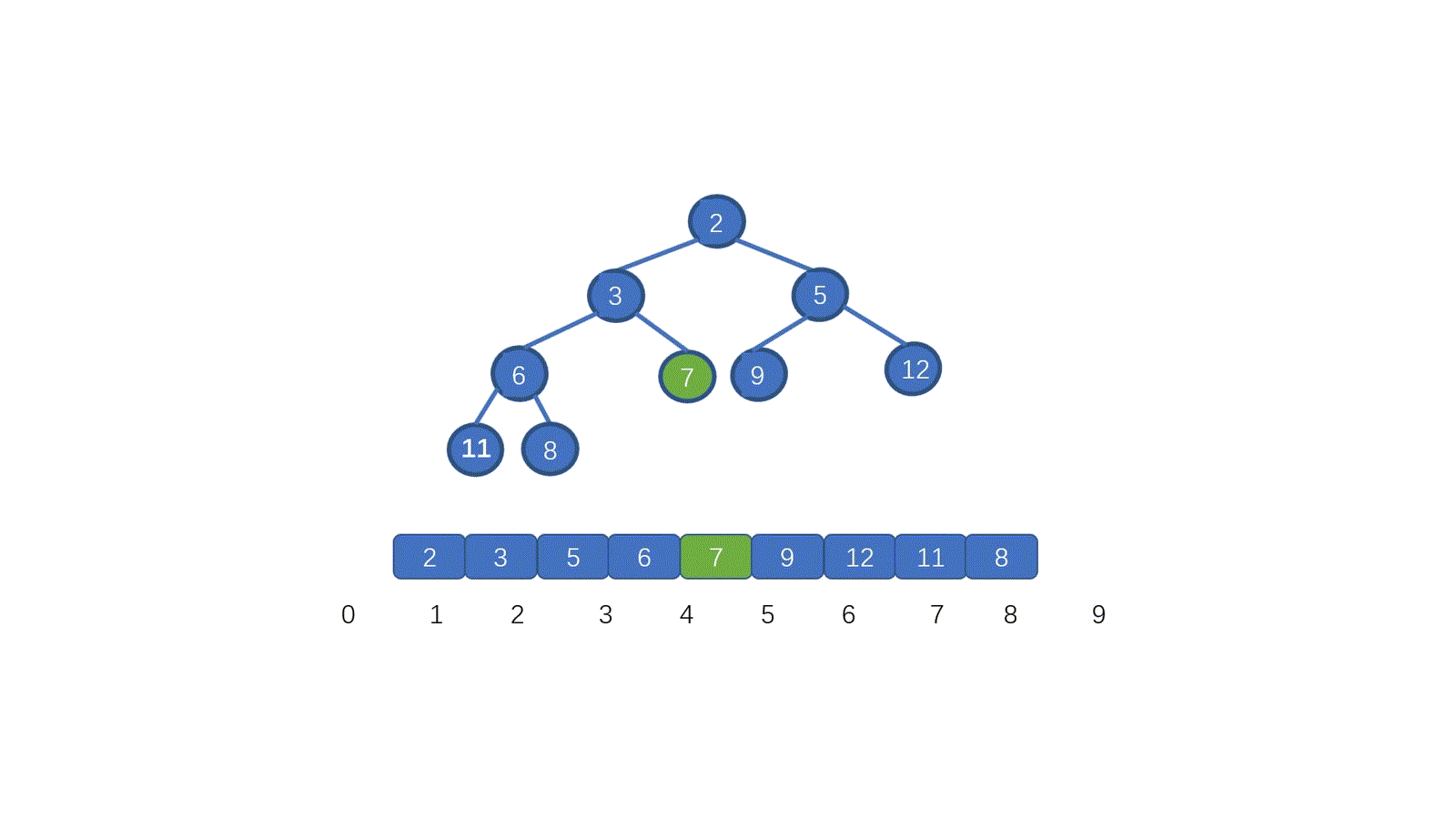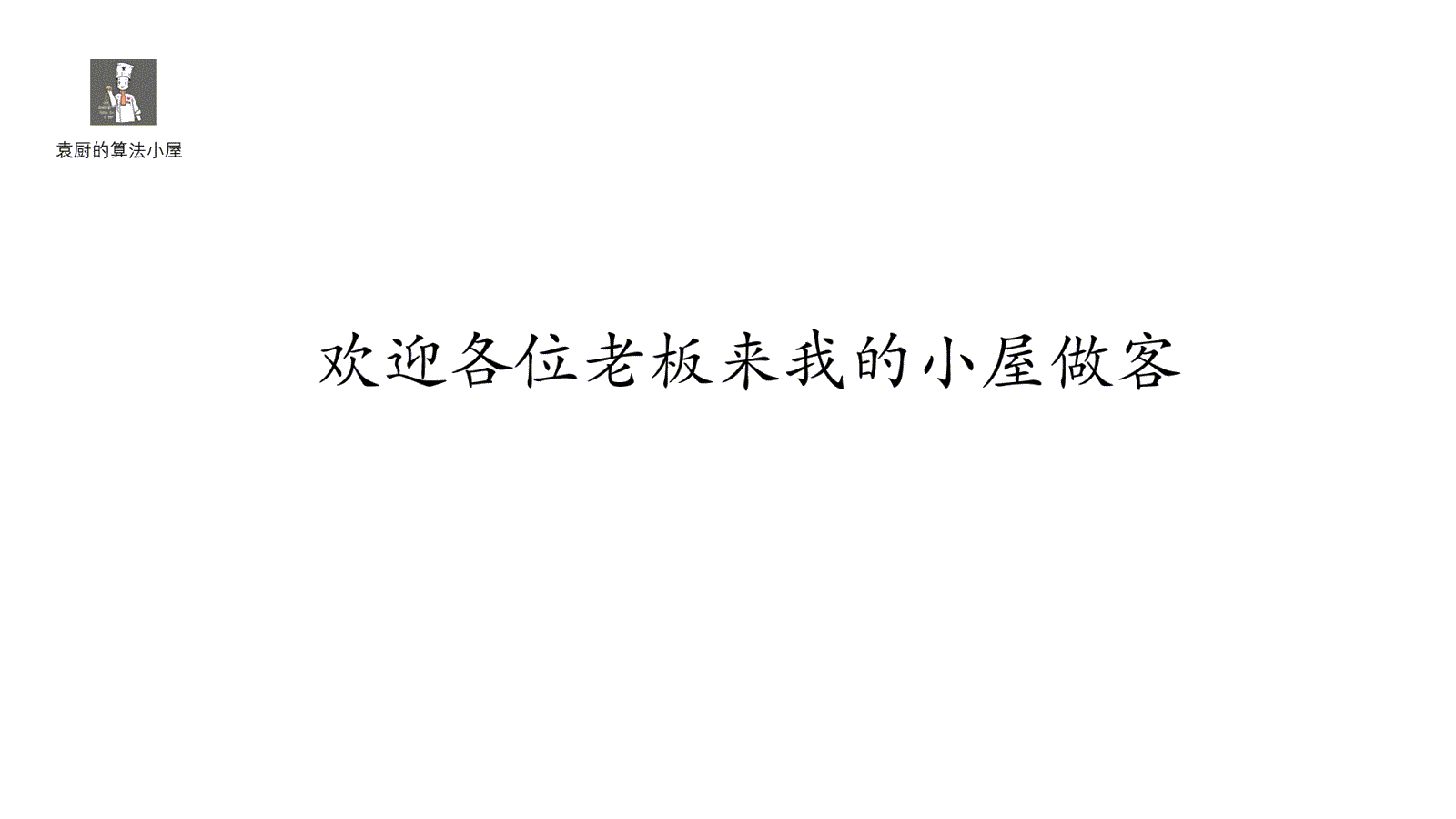
看完視頻是不是懂個大概了，但是不知道大家有沒有注意到這個地方。為什么 7 第一次與其左孩子節點 2 交換，第二次與右孩子節點 3 交換。見下圖

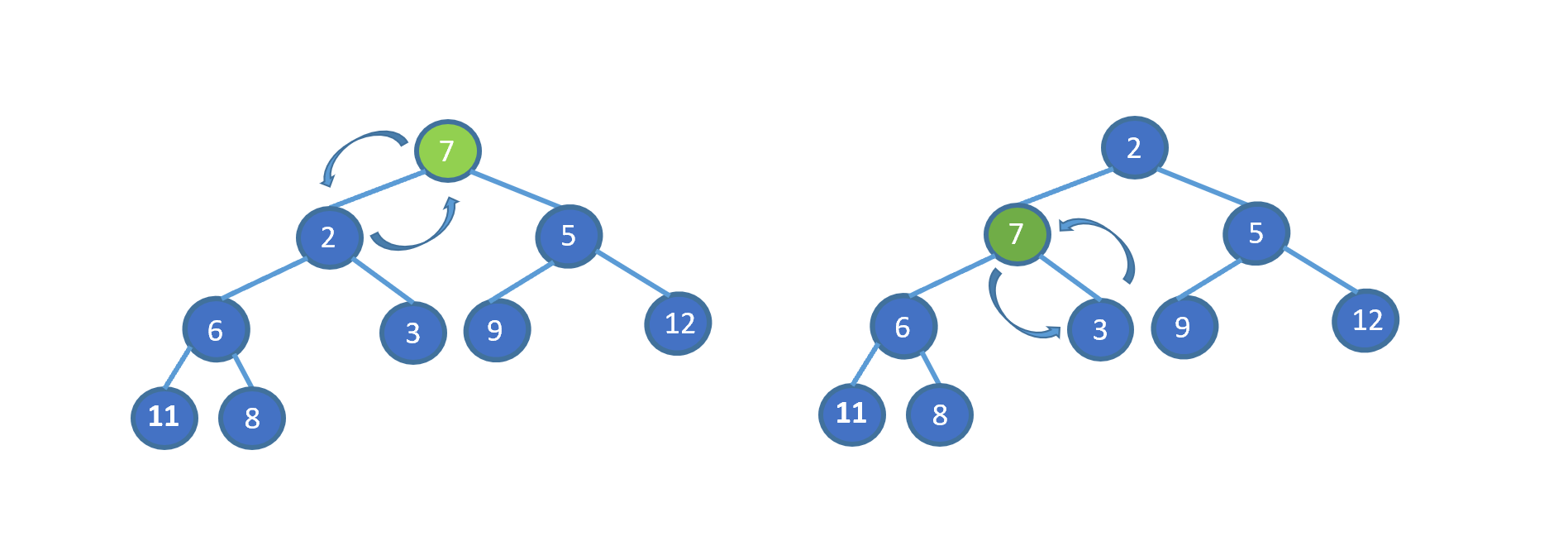
其實很容易理解，我們需要與孩子節點中最小的那個交換，因為我們需要交換后，父節點小于兩個孩子節點，如果我們第一步，7 與 5 進行交換的話，則同樣不能滿足小頂堆。

那我們怎么判斷節點找到屬于它的位置了呢？主要有兩個情況

• 待下沉元素小于（大于）兩個子節點，此時符合堆的規則，無序下沉，例如上圖中的 6
• 下沉為葉子節點，此時沒有子節點，例如 7 下沉到最后變成了葉子節點。

我們將上面的操作稱之為下沉操作。

這時我們又有疑問了，下沉操作我懂了，但是這跟建堆有個錘子關系啊！

不要急，我們繼續來看視頻，這次我們通過下沉操作建個大頂堆。

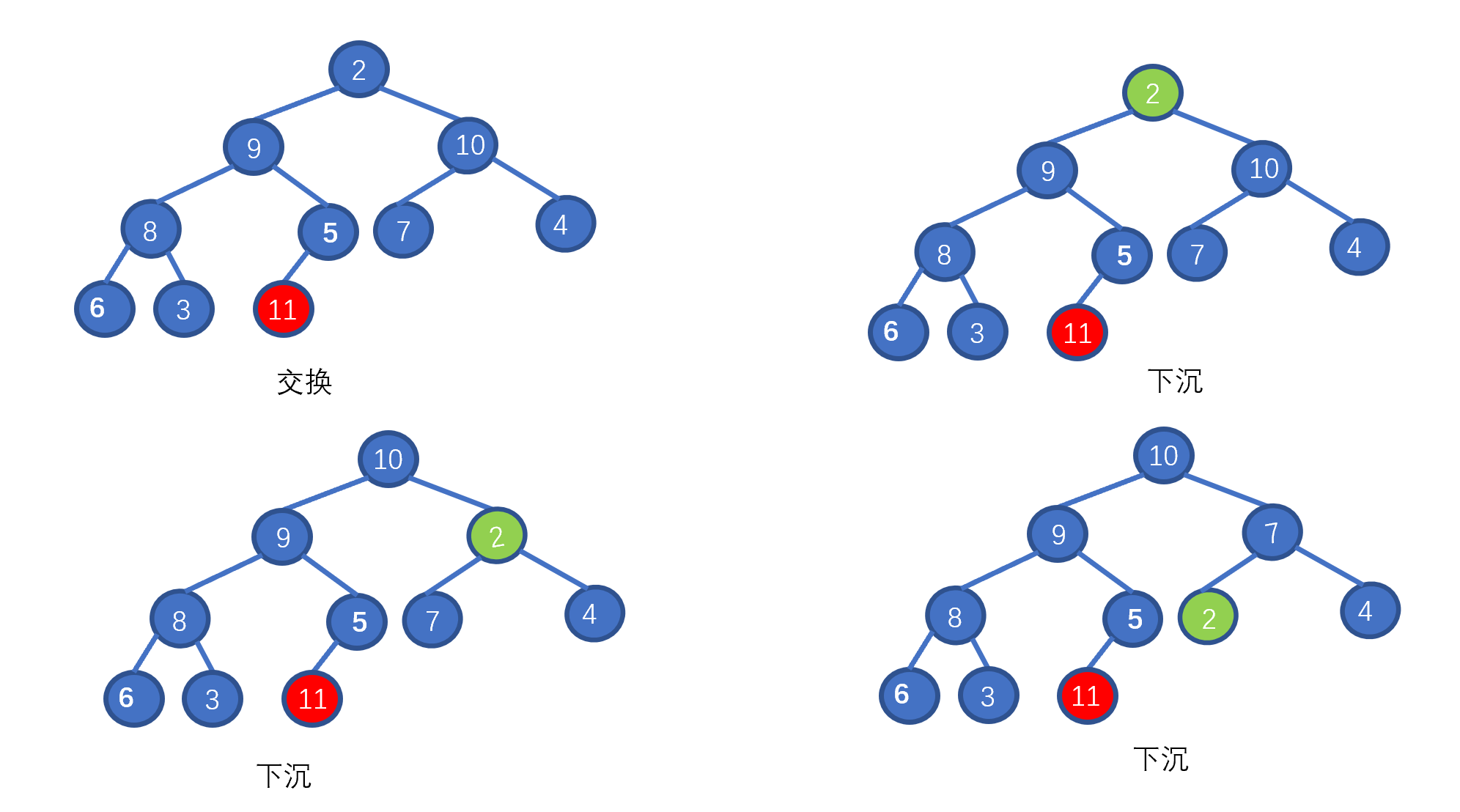
初始數組 [8,5,7,9,2,10,1,4,6,3]

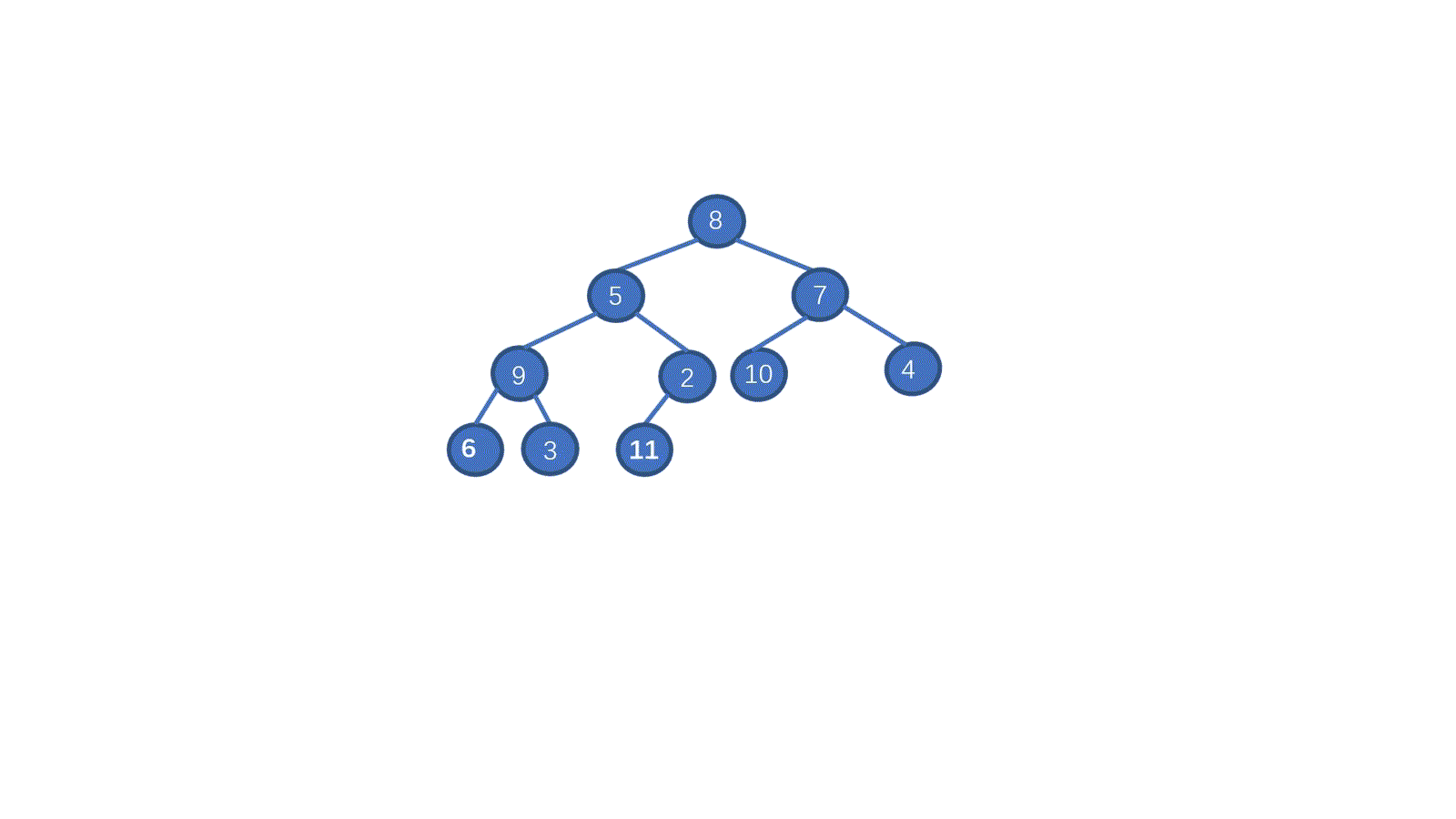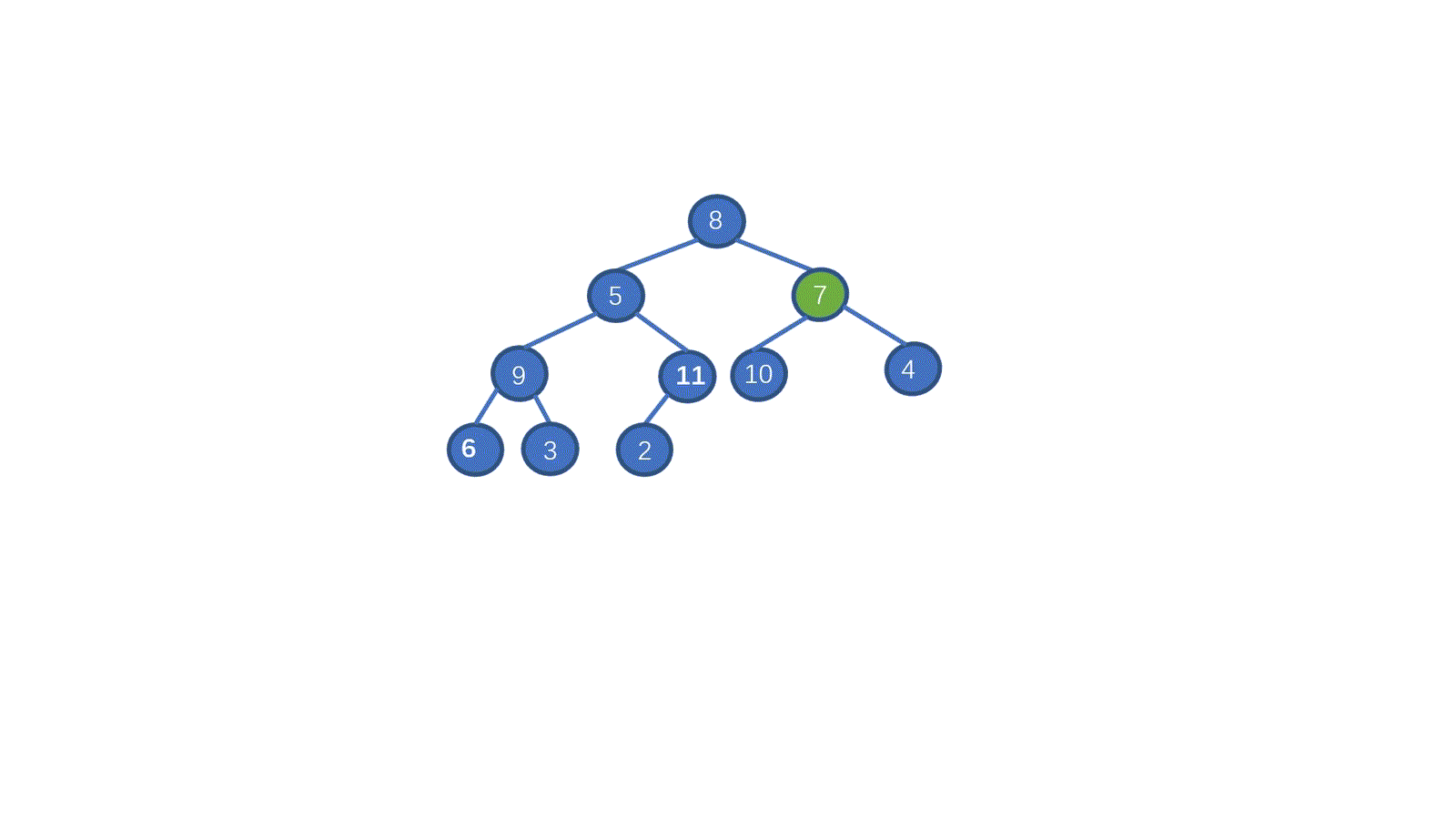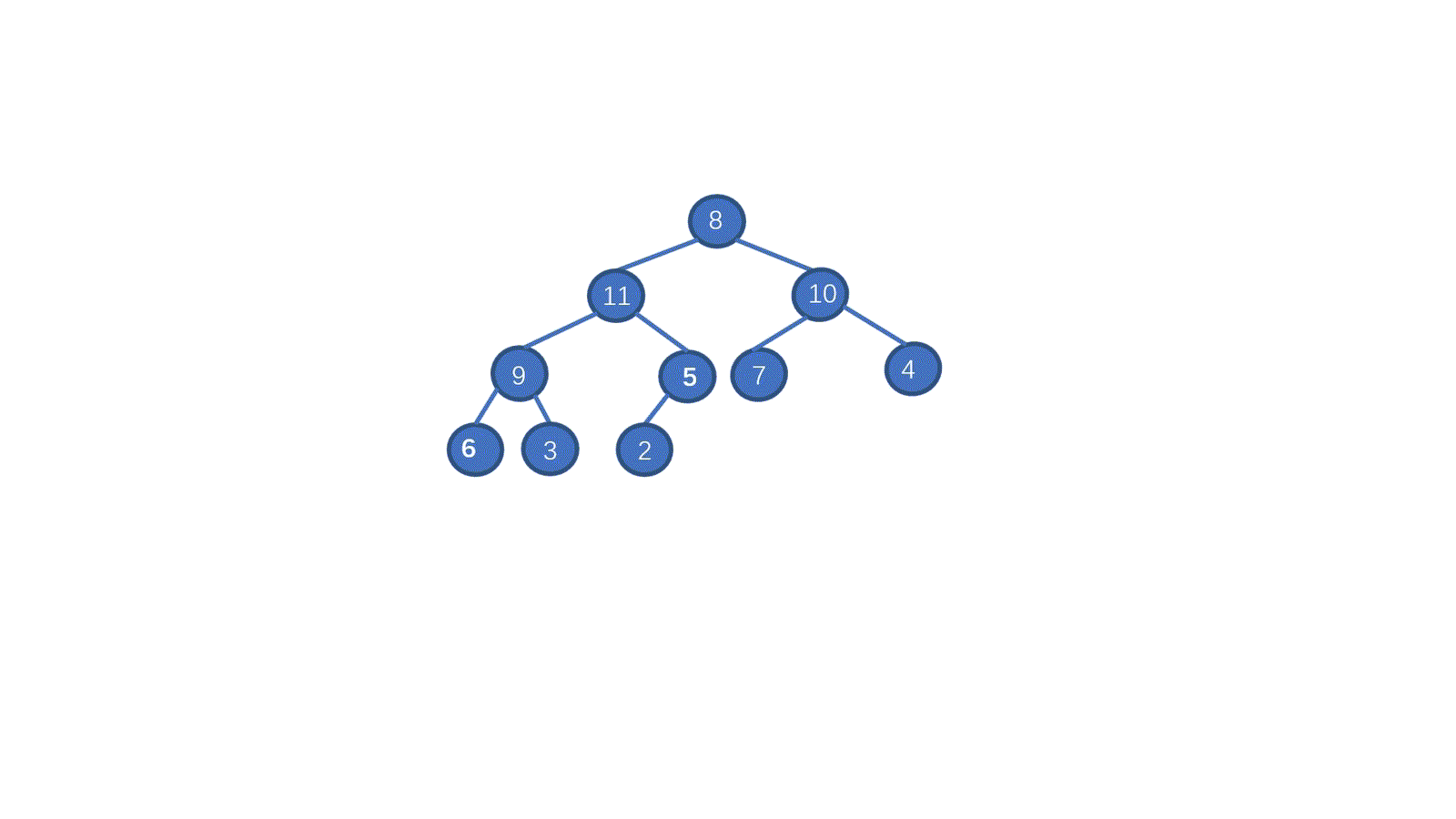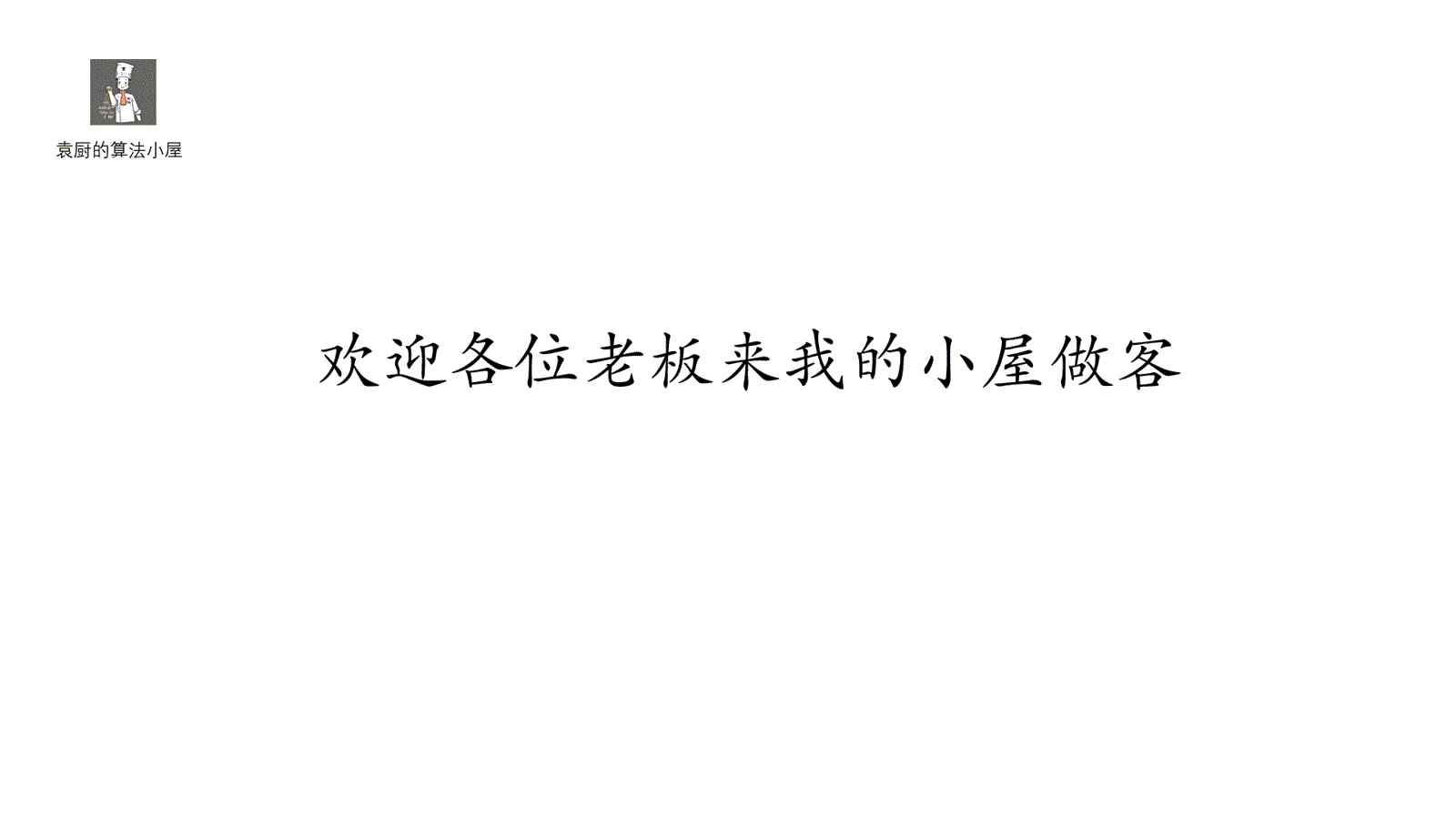
我們一起來拆解一下視頻，我們只需要從最后一個非葉子節點開始，依次執行下沉操作。執行完畢后我們就能夠完成堆化。是不是一下就懂了呀。

好啦我們一起看哈下沉操作的代碼吧。

public void sink (int[] nums, int index,int len) {while (true) {//獲取子節點int j = 2 * index;if (j < len-1 && nums[j] < nums[j+1]) {j++;}//交換操作，父節點下沉，與最大的孩子節點交換if (j < len && nums[index] < nums[j]) {swap(nums,index,j);} else {break;} //繼續下沉index = j;}}

好啦，兩種建堆方式我們都已經了解啦，那么我們如何進行排序呢？

了解排序之前我們先來，看一下如何刪除堆頂元素，我們需要保證的是，刪除堆頂元素后，其他元素仍能滿足堆的要求，我們思考一下如何實現呢？見下圖

假設我們想要去除堆頂的 11 ，那我們則需要將其與堆的最后一個節點交換也就是 2 ，2然后再執行下沉操作，執行完畢后仍能滿足堆的要求，見下圖

好啦，其實你已經學會如何排序啦！你不信？那我給你放視頻

好啦，大家是不是已經搞懂啦，下面我們總結一下堆排序的具體執行過程

1.建堆，通過下沉操作建堆效率更高，具體過程是，找到最后一個非葉子節點，然后從后往前遍歷執行下沉操作。

2.排序，將堆頂元素（代表最大元素）與最后一個元素交換，然后新的堆頂元素進行下沉操作，遍歷執行上訴操作，則可以完成排序。

好啦，下面我們一起看代碼吧

class Solution {public int[] sortArray(int[] nums) {int len = nums.length;int[] a = new int[len + 1];for (int i = 0; i < nums.length; ++i) {a[i+1] = nums[i];}          //下沉建堆for (int i = len/2; i >= 1; --i) {sink(a,i,len);}int k = len;//排序while (k > 1) {swap(a,1,k--);sink(a,1,k);}for (int i = 1; i < len+1; ++i) {nums[i-1] = a[i];}return nums;}public void sink (int[] nums, int k,int end) {//下沉while (2 * k <= end) {int j = 2 * k;//找出子節點中最大或最小的那個if (j + 1 <= end && nums[j + 1] > nums[j]) {j++;}if (nums[j] > nums[k]) {swap(nums, j, k);} else {break;}k = j;}}public void swap (int nums[], int i, int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}}

好啦，堆排序我們就到這里啦，是不是搞定啦，總的來說堆排序比其他排序算法稍微難理解一些，重點就是建堆，而且應用比較廣泛，大家記得打卡呀。

好啦，我們再來分析一下堆排序的時間復雜度、空間復雜度以及穩定性。

堆排序時間復雜度分析

因為我們建堆的時間復雜度為 O(n），排序過程的時間復雜度為 O(nlogn),所以總的空間復雜度為 O(nlogn)

堆排序空間復雜度分析

這里需要注意，我們上面的描述過程中，為了更直觀的描述，空出數組的第一位，這樣我們就可以通過 i * 2 和 i * 2+1 來求得左孩子節點和右孩子節點 。我們也可以根據 i * 2 + 1 和 i * 2 + 2 來獲取孩子節點，這樣則不需要臨時數組來處理原數組，將所有元素后移一位，所以堆排序的空間復雜度為 O(1),是原地排序算法。

堆排序穩定性分析

堆排序不是穩定的排序算法，在排序的過程，我們會將堆的最后一個節點跟堆頂節點交換，改變相同元素的原始相對位置。

最后我們來比較一下我們快速排序和堆排序

1.對于快速排序來說，數據是順序訪問的。而對于堆排序來說，數據是跳著訪問的。這樣對 CPU 緩存是不友好的

2.相同的的數據，排序過程中，堆排序的數據交換次數要多于快速排序。

所以上面兩條也就說明了在實際開發中，堆排序的性能不如快速排序性能好。

好啦，今天的內容就到這里啦，咱們下期見。

---

歸并排序

歸并排序是必須要掌握的排序算法，也算是面試高頻考點，下面我們就一起來扒一扒歸并排序吧，原理很簡單，大家一下就能搞懂。

袁記菜館內

第 23 屆食神爭霸賽開賽啦！

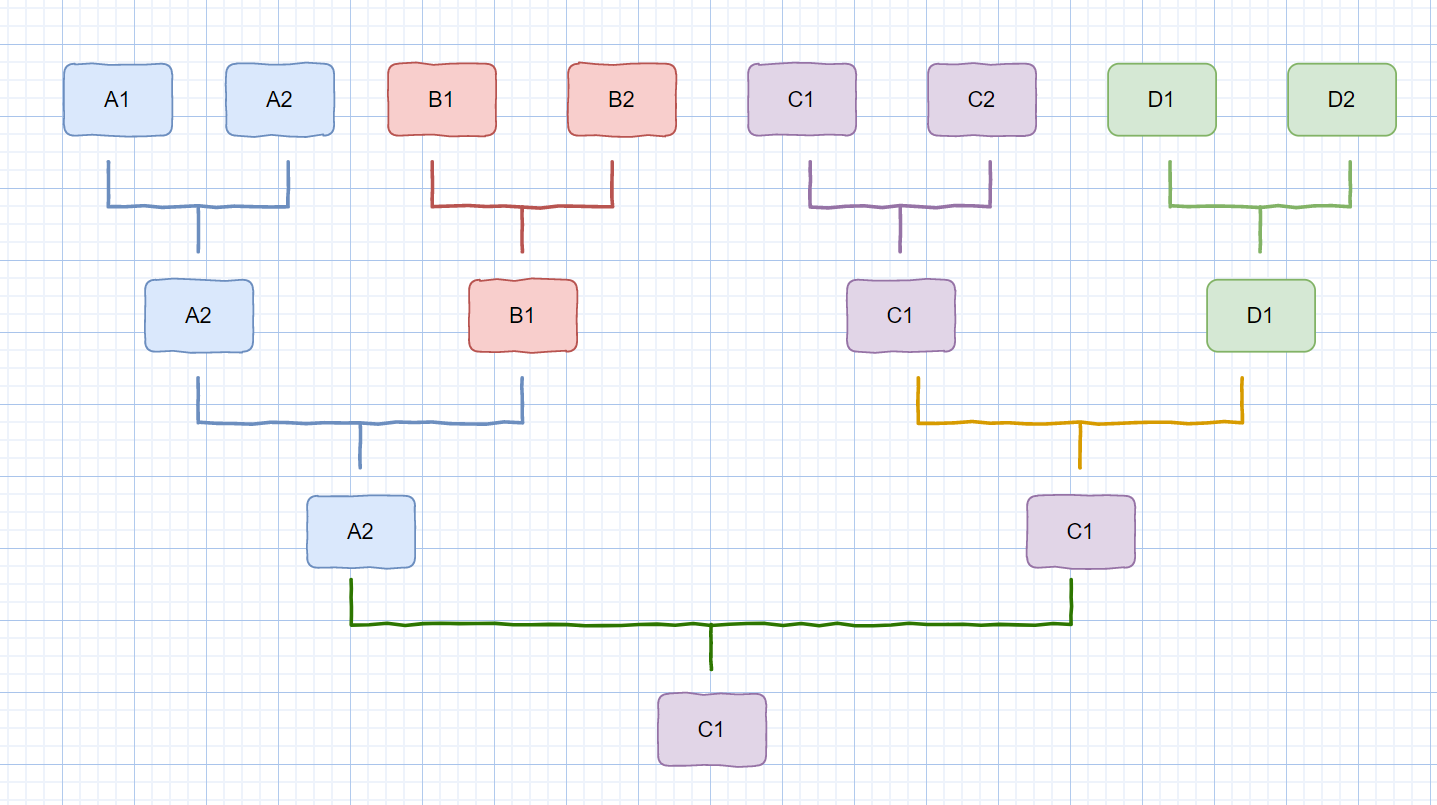
袁廚想在自己排名前4的分店中，挑選一個最優秀的廚師來參加食神爭霸賽，選拔規則如下。

第一場 PK：每個分店選出兩名廚師，首先進行店內 PK,選出店內里的勝者

第二場 PK: 然后店內的優勝者代表分店挑戰其他某一分店的勝者（半決賽）

第三場 PK：最后剩下的兩名勝者進行PK,選出最后的勝者。

示意圖如下

上面的例子大家應該不會陌生吧，其實我們歸并排序和食神選拔賽的流程是有些相似的，下面我們一起來看一下吧

歸并這個詞語的含義就是合并，并入的意思，而在我們的數據結構中的定義是將兩個或兩個以上的有序表和成一個新的有序表。而我們這里說的歸并排序就是使用歸并的思想實現的排序方法。

歸并排序使用的就是分治思想。顧名思義就是分而治之，將一個大問題分解成若干個小的子問題來解決。小的子問題解決了，大問題也就解決了。分治后面會專門寫一篇文章進行描述滴，這里先簡單提一下。

下面我們通過一個圖片來描述一下歸并排序的數據變換情況，見下圖。

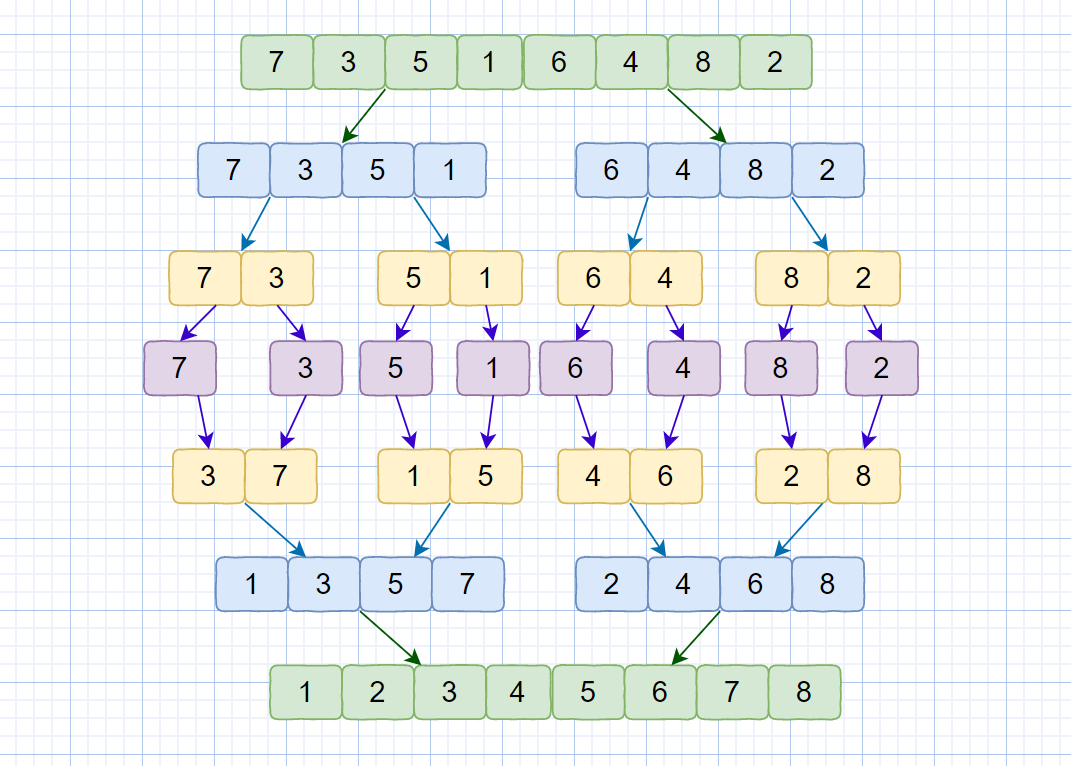
我們簡單了解了歸并排序的思想，從上面的描述中，我們可以知道算法的歸并過程是比較難實現的，這也是這個算法的重點，看完我們這個視頻就能懂個大概啦。

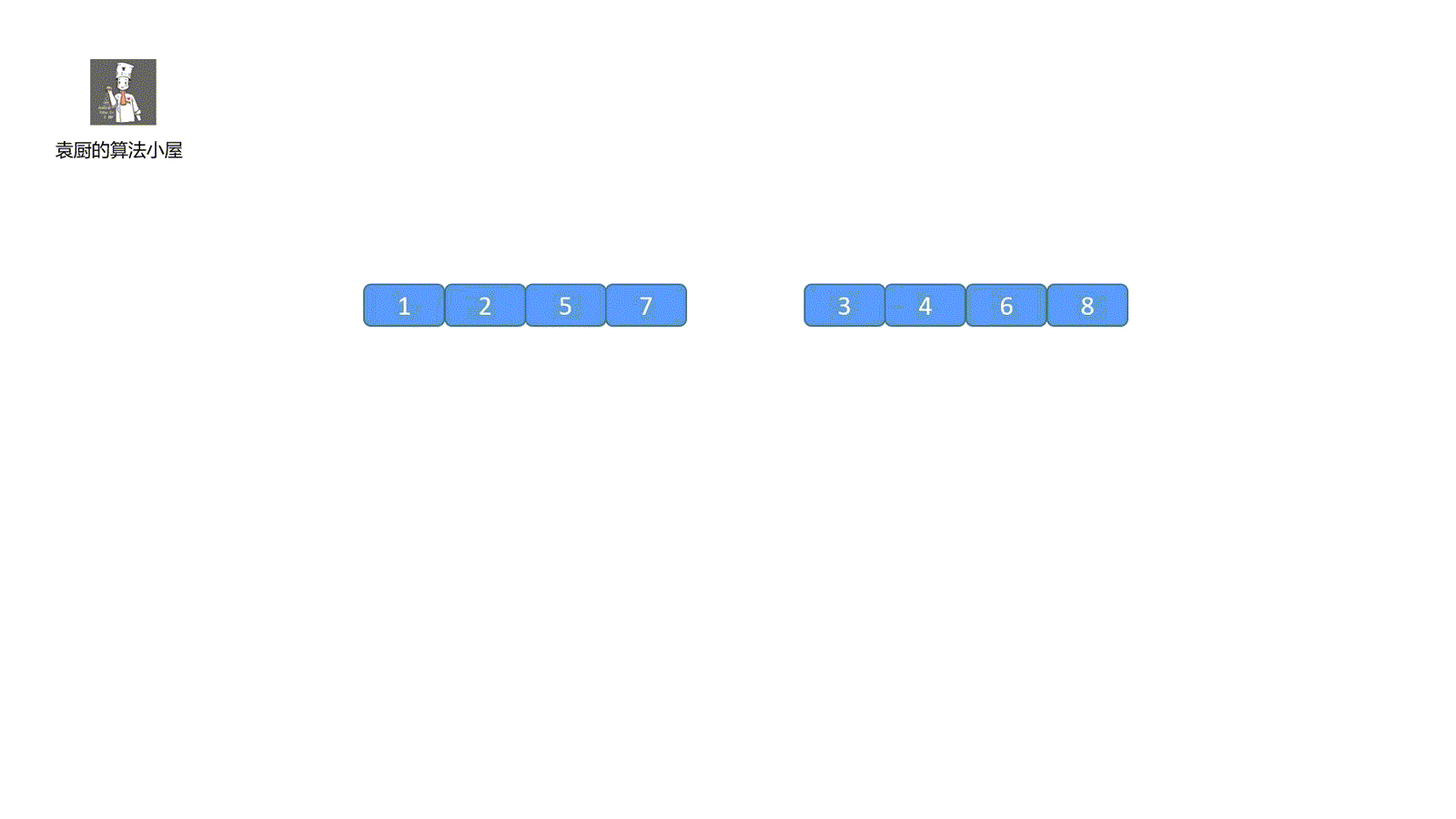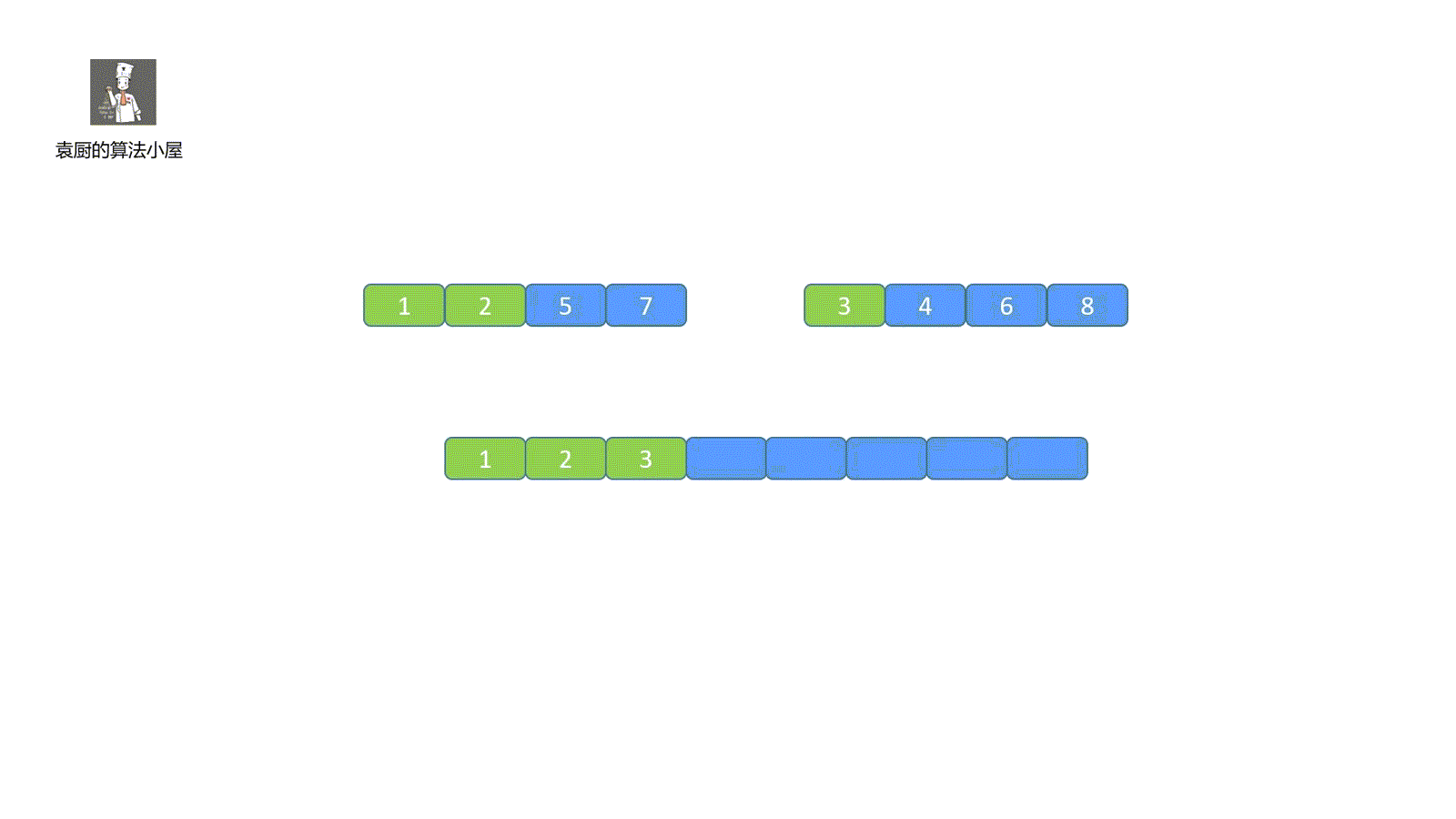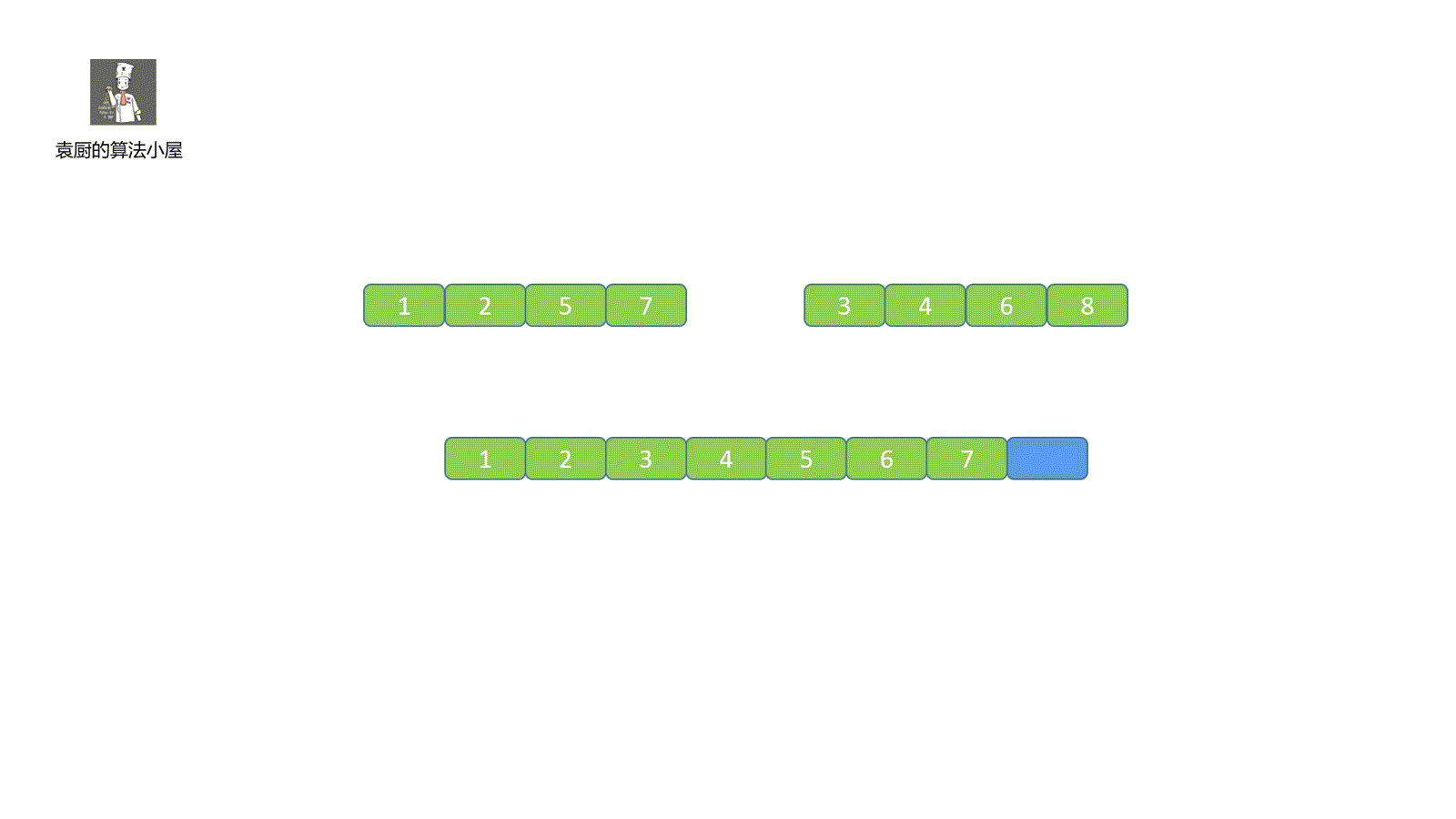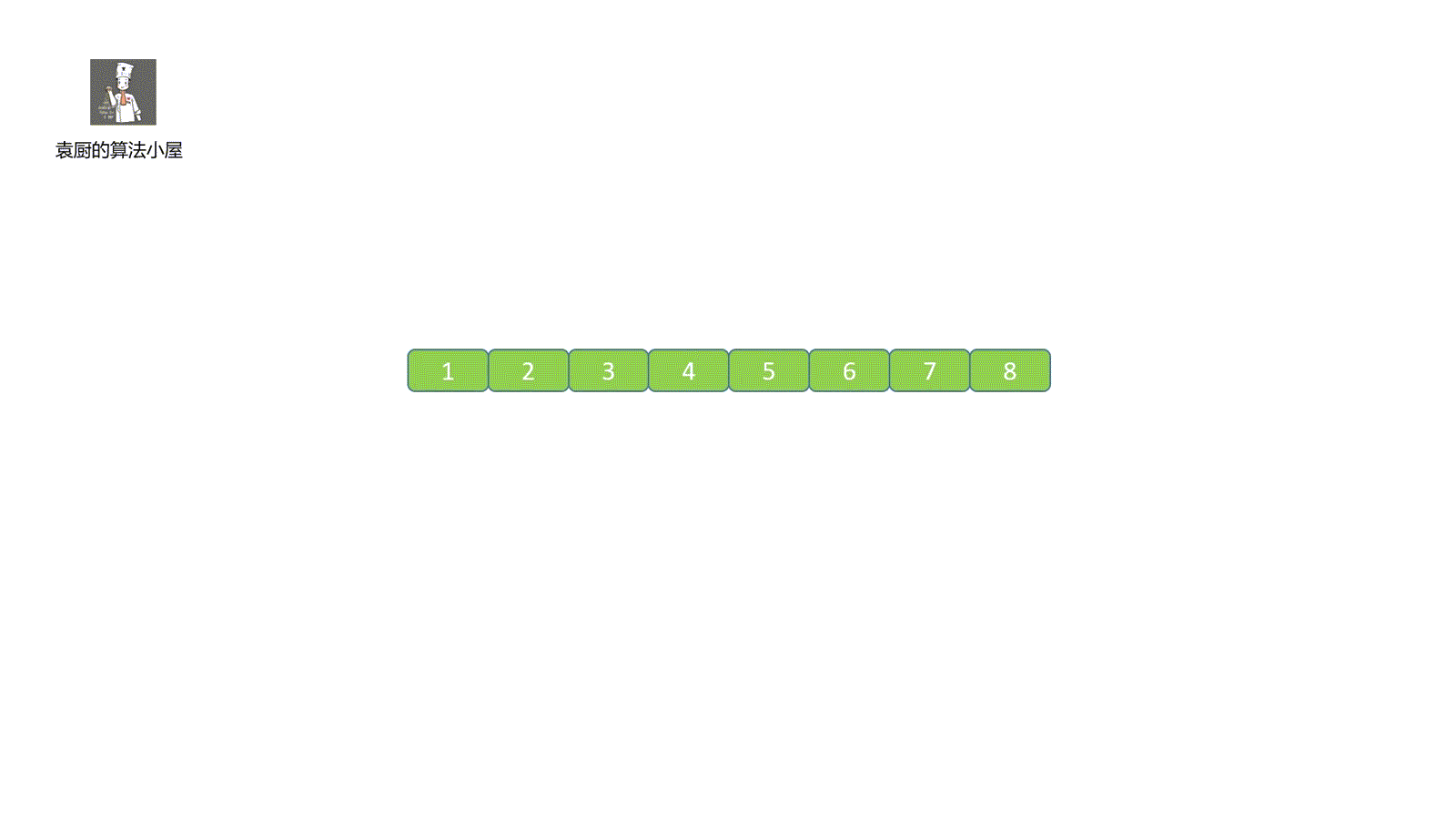
視頻中歸并步驟大家有沒有看懂呀，沒看懂也不用著急，下面我們一起來拆解一下，歸并共有三步走。

第一步：創建一個額外大集合用于存儲歸并結果，長度則為那兩個小集合的和，從視頻中也可以看的出

第二步：我們從左自右比較兩個指針指向的值，將較小的那個存入大集合中，存入之后指針移動，并繼續比較，直到某一小集合的元素全部都存到大集合中。見下圖

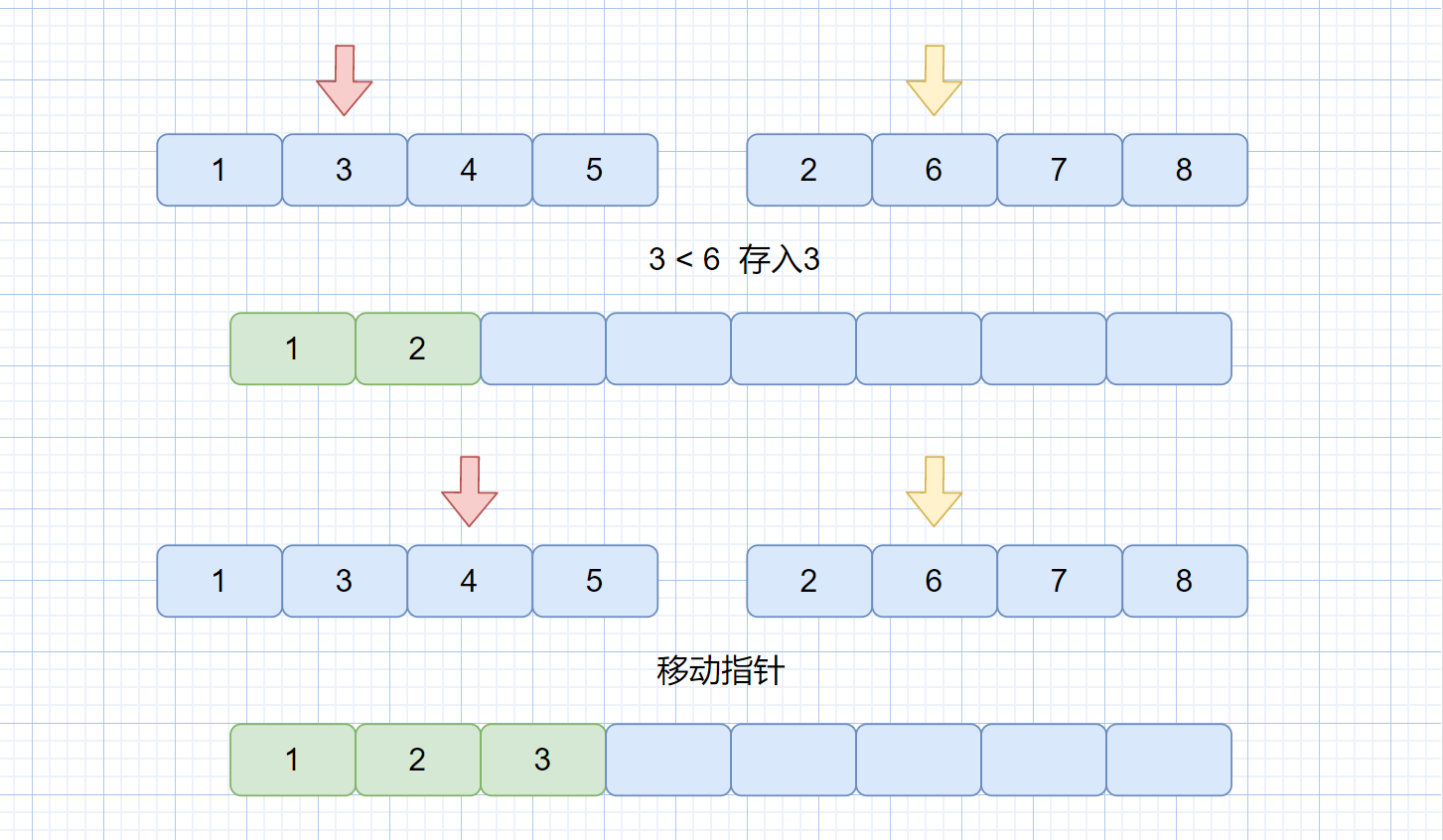
第三步：當某一小集合元素全部放入大集合中，則需將另一小集合中剩余的所有元素存到大集合中，見下圖

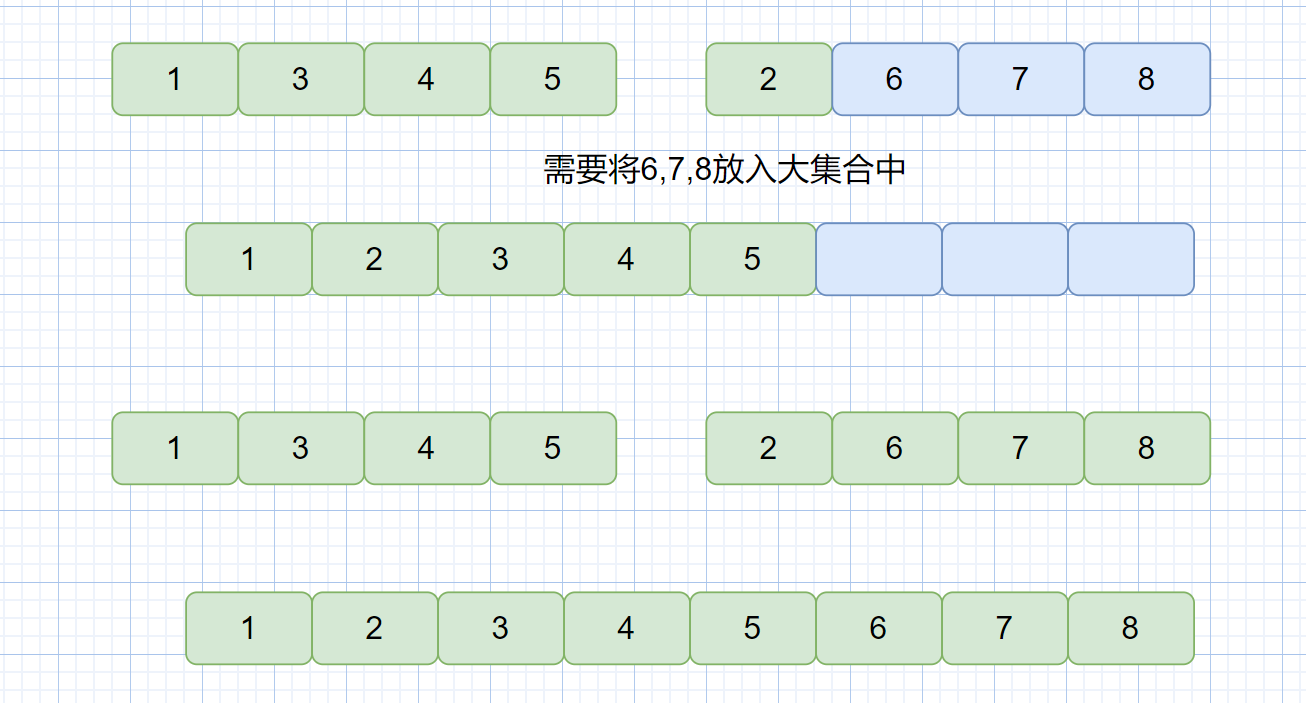
好啦，看完視頻和圖解是不是能夠寫出個大概啦，了解了算法原理之后代碼寫起來就很簡單啦，

遞歸實現

下面我們看代碼吧。

class Solution {public int[] sortArray(int[] nums) {mergeSort(nums,0,nums.length-1);return nums;}public void mergeSort(int[] arr, int left, int right) {if (left < right) {int mid = left + ((right - left) >> 1);mergeSort(arr,left,mid);mergeSort(arr,mid+1,right);merge(arr,left,mid,right);}} //歸并public void merge(int[] arr,int left, int mid, int right) {//第一步，定義一個新的臨時數組int[] temparr = new int[right -left + 1];int temp1 = left, temp2 = mid + 1;int index = 0;//對應第二步，比較每個指針指向的值，小的存入大集合while (temp1 <= mid && temp2 <= right) {if (arr[temp1] <= arr[temp2]) {temparr[index++] = arr[temp1++];} else {temparr[index++] = arr[temp2++];}}//對應第三步，將某一小集合的剩余元素存到大集合中if (temp1 <= mid) System.arraycopy(arr, temp1, temparr, index, mid - temp1 + 1);if (temp2 <= right) System.arraycopy(arr, temp2, temparr, index, right -temp2 + 1);     //將大集合的元素復制回原數組System.arraycopy(temparr,0,arr,0+left,right-left+1); }
}

歸并排序時間復雜度分析

我們一趟歸并，需要將兩個小集合的長度放到大集合中，則需要將待排序序列中的所有記錄掃描一遍所以時間復雜度為O(n)。歸并排序把集合一層一層的折半分組，則由完全二叉樹的深度可知，整個排序過程需要進行 logn（向上取整）次,則總的時間復雜度為 O(nlogn)。另外歸并排序的執行效率與要排序的原始數組的有序程度無關，所以在最好，最壞，平均情況下時間復雜度均為 O(nlogn) 。雖然歸并排序時間復雜度很穩定，但是他的應用范圍卻不如快速排序廣泛，這是因為歸并排序不是原地排序算法，空間復雜度不為 O(1)，那么他的空間復雜度為多少呢？

歸并排序的空間復雜度分析

歸并排序所創建的臨時結合都會在方法結束時釋放，單次歸并排序的最大空間是 n ,所以歸并排序的空間復雜度為 O(n).

歸并排序的穩定性分析

歸并排序的穩定性，要看我們的 merge 函數，我們代碼中設置了 arr[temp1] <= arr[temp2] ，當兩個元素相同時，先放入arr[temp1] 的值到大集合中，所以兩個相同元素的相對位置沒有發生改變，所以歸并排序是穩定的排序算法。

算法名稱	最好時間復雜度	最壞時間復雜度	平均時間復雜度	空間復雜度	是否穩定
歸并排序	O(nlogn)	O(nlogn)	O(nlogn)	O(n)	穩定

等等還沒完嘞，不要走。

迭代實現

歸并排序的遞歸實現是比較常見的，也是比較容易理解的，下面我們一起來扒一下歸并排序的迭代寫法。看看他是怎么實現的。

我們通過一個視頻來了解下迭代方法的思想，

是不是通過視頻了解個大概啦，下面我們來對視頻進行解析。

迭代實現的歸并排序是將小集合合成大集合，小集合大小為 1,2,4,8,.....。依次迭代，見下圖

比如此時小集合大小為 1 。兩個小集合分別為 [3],[1]。然后我們根據合并規則，見第一個視頻，將[3],[1]合并到臨時數組中，則小的先進，則實現了排序，然后再將臨時數組的元素復制到原來數組中。則實現了一次合并。

下面則繼續合并[4],[6]。具體步驟一致。所有的小集合合并完成后，則小集合的大小變為 2，繼續執行剛才步驟，見下圖。

此時子集合的大小為 2 ，則為 [2,5],[1,3] 繼續按照上面的規則合并到臨時數組中完成排序。 這就是迭代法的具體執行過程，

下面我們直接看代碼吧。

注：遞歸法和迭代法的 merge函數代碼一樣。

class Solution {public int[] sortArray (int[] nums) {//代表子集合大小，1，2，4，8，16.....int k = 1;int len = nums.length;while (k < len) {mergePass(nums,k,len);k *= 2;}return nums;}public void mergePass (int[] array, int k, int len) {int i;for (i = 0; i < len-2*k; i += 2*k) {//歸并merge(array,i,i+k-1,i+2*k-1);}//歸并最后兩個序列if (i + k < len) {merge(array,i,i+k-1,len-1);}}public void merge (int[] arr,int left, int mid, int right) {//第一步，定義一個新的臨時數組int[] temparr = new int[right -left + 1];int temp1 = left, temp2 = mid + 1;int index = 0;//對應第二步，比較每個指針指向的值，小的存入大集合while (temp1 <= mid && temp2 <= right) {if (arr[temp1] <= arr[temp2]) {temparr[index++] = arr[temp1++];} else {temparr[index++] = arr[temp2++];}}//對應第三步，將某一小集合的剩余元素存到大集合中if (temp1 <= mid) System.arraycopy(arr, temp1, temparr, index, mid - temp1 + 1);if (temp2 <= right) System.arraycopy(arr, temp2, temparr, index, right -temp2 + 1);   //將大集合的元素復制回原數組System.arraycopy(temparr,0,arr,0+left,right-left+1); }
}

計數排序

今天我們就一起來看看線性排序里的計數排序到底是怎么回事吧。

我們將鏡頭切到袁記菜館

因為今年袁記菜館的效益不錯，所以袁廚就想給員工發些小福利，讓小二根據員工工齡進行排序，但是菜館共有 100000 名員工，菜館開業 10 年，員工工齡從 0 - 10 不等。看來這真是一個艱巨的任務啊。

當然我們可以借助之前說過的 歸并排序 和 快速排序解決，但是我們有沒有其他更好的方法呢？

了解排序算法的老哥可能已經猜到今天寫什么啦。是滴，我們今天來寫寫用空間換時間的線性排序。

說之前我們先來回顧一下之前的排序算法，最好的時間復雜度為 O(nlogn) ,且都基于元素之間的比較來進行排序，

我們來說一下非基于元素比較的排序算法，且時間復雜度為 O（n），時間復雜度是線性的，所以我們稱其為線性排序算法。

其優勢在于在對一定范圍內的整數排序時，它的復雜度為Ο(n+k)，此時的 k 則代表整數的范圍。快于任何一種比較類排序算法，不過也是需要犧牲一些空間來換取時間。

下面我們先來看看什么是計數排序，這個計數的含義是什么？

我們假設某一分店共有 10 名員工，

工齡分別為 1，2，3，5，0，2，2，4，5，9

那么我們將其存在一個長度為 10 的數組里，，但是我們注意，我們數組此時存的并不是元素值，而是元素的個數。見下圖

注：此時我們這里統計次數的數組根據最大值來決定，上面的例子中最大值為 9 ，則長度為 9 + 1 = 10。暫且先這樣理解，后面會對其優化 。

我們繼續以上圖的例子來說明，在該數組中，索引代表的為元素值（也就是上面例子中的工齡），數組的值代表的則是元素個數（也就是不同工齡出現的次數）。

即工齡為 0 的員工有 1 個， 工齡為 1 的員工有 1 個，工齡為 2 的員工有 3 個 。。。

然后我們根據出現次數將其依次取出看看是什么效果。

0，1，2，2，2，3，4，5，5，9

我們發現此時元素則變成了有序的，但是這并不是排序，只是簡單的按照統計數組的下標，輸出了元素值，并沒有真正的給原始數組進行排序。

這樣操作之后我們不知道工齡屬于哪個員工。

見下圖

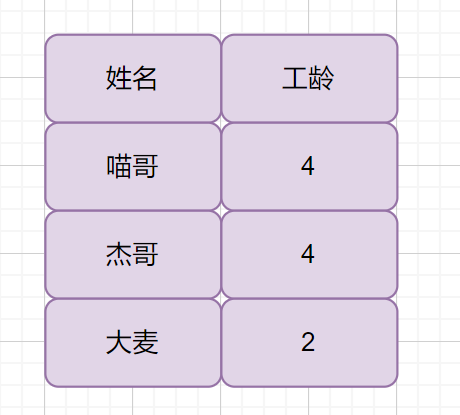
雖然喵哥和杰哥工齡相同，如果我們按照上面的操作輸出之后，我們不能知道工齡為 4 的兩個員工，哪個是喵哥哪個是杰哥。

所以我們需要借助其他方法來對元素進行排序。

大家還記不記得我們之前說過的前綴和，下面我們通過上面統計次數的數組求出其前綴和數組。

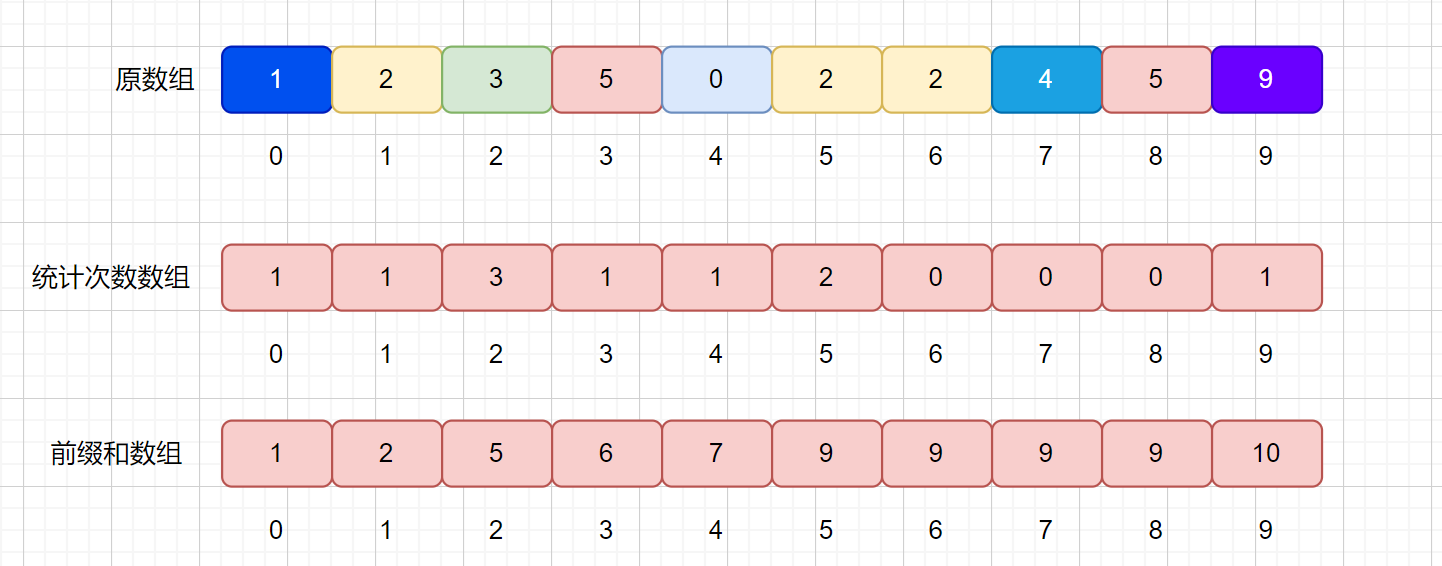
因為我們是通過統計次數的數組得到了前綴和數組，那么我們來分析一下 presum 數組里面值的含義。

例如我們的 presum[2] = 5 ,代表的則是原數組小于等于 2 的值共有 5 個。presum[4] = 7 代表小于等于 4 的元素共有 7 個。

是不是感覺計數排序的含義要慢慢顯現出來啦。

其實到這里我們已經可以理解的差不多了，還差最后一步，

此時我們要從后往前遍歷原始數組，然后將遍歷到的元素放到臨時數組的合適位置，并修改 presum 數組的值，遍歷結束后則達到了排序的目的。

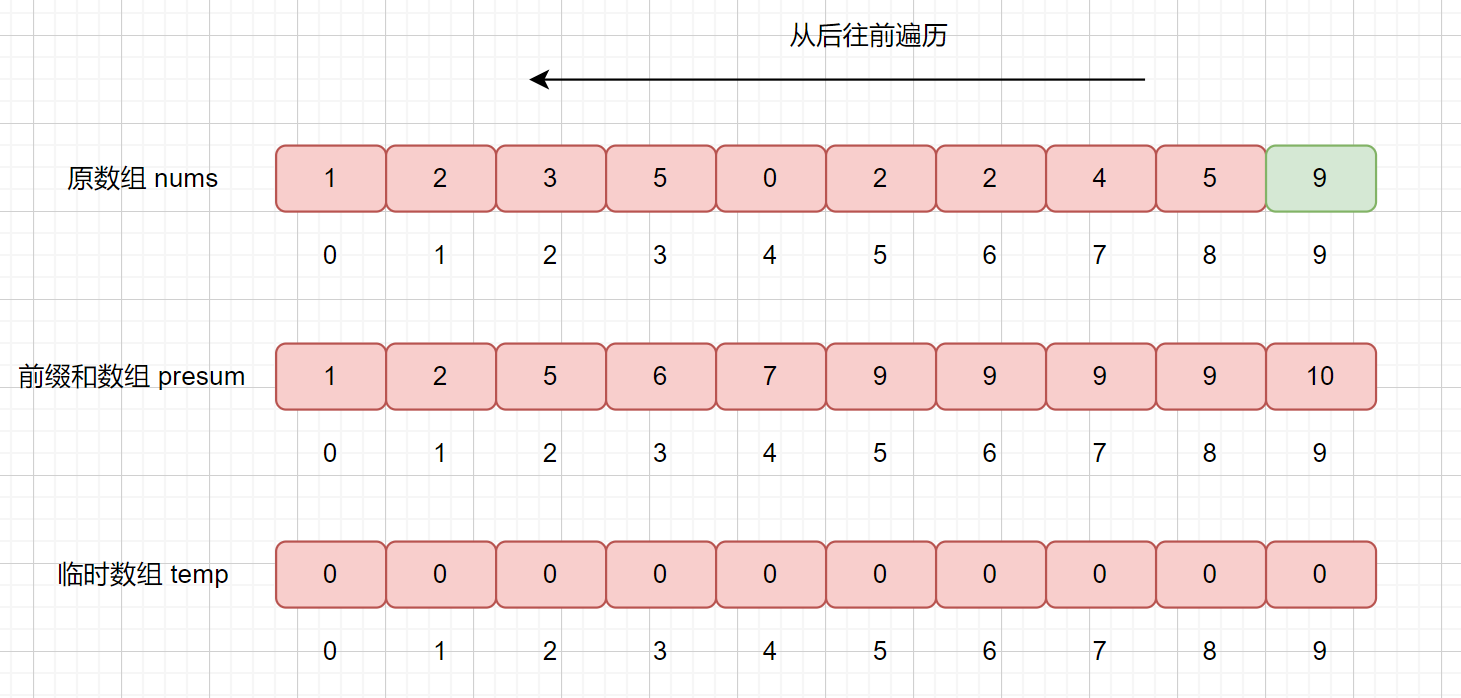
我們從后往前遍歷，nums[9] = 9,則我們拿該值去 presum 數組中查找，發現 presum[nums[9]] = presum[9] = 10 ，大家還記得我們 presum 數組里面每個值得含義不，我們此時 presum[9] = 10,則代表在數組中，小于等于的數共有 10 個，則我們要將他排在臨時數組的第 10 個位置，也就是 temp[9] = 9。

我們還需要干什么呢？我們想一下，我們已經把 9 放入到 temp 數組里了，已經對其排好序了，那么我們的 presum 數組則不應該再統計他了，則將相應的位置減 1 即可，也就是 presum[9] = 10 - 1 = 9;

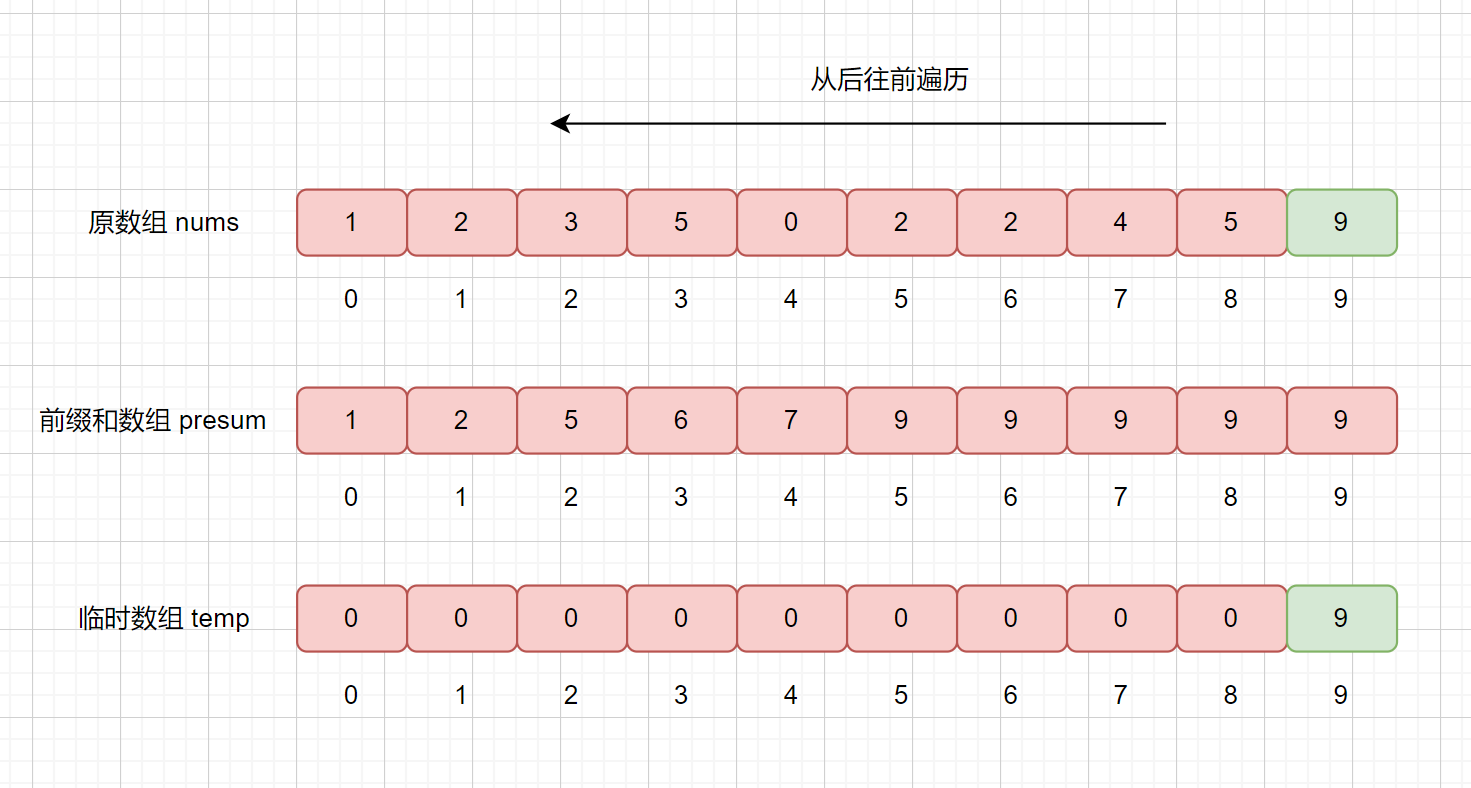
下面我們繼續遍歷 5 ，然后同樣執行上訴步驟

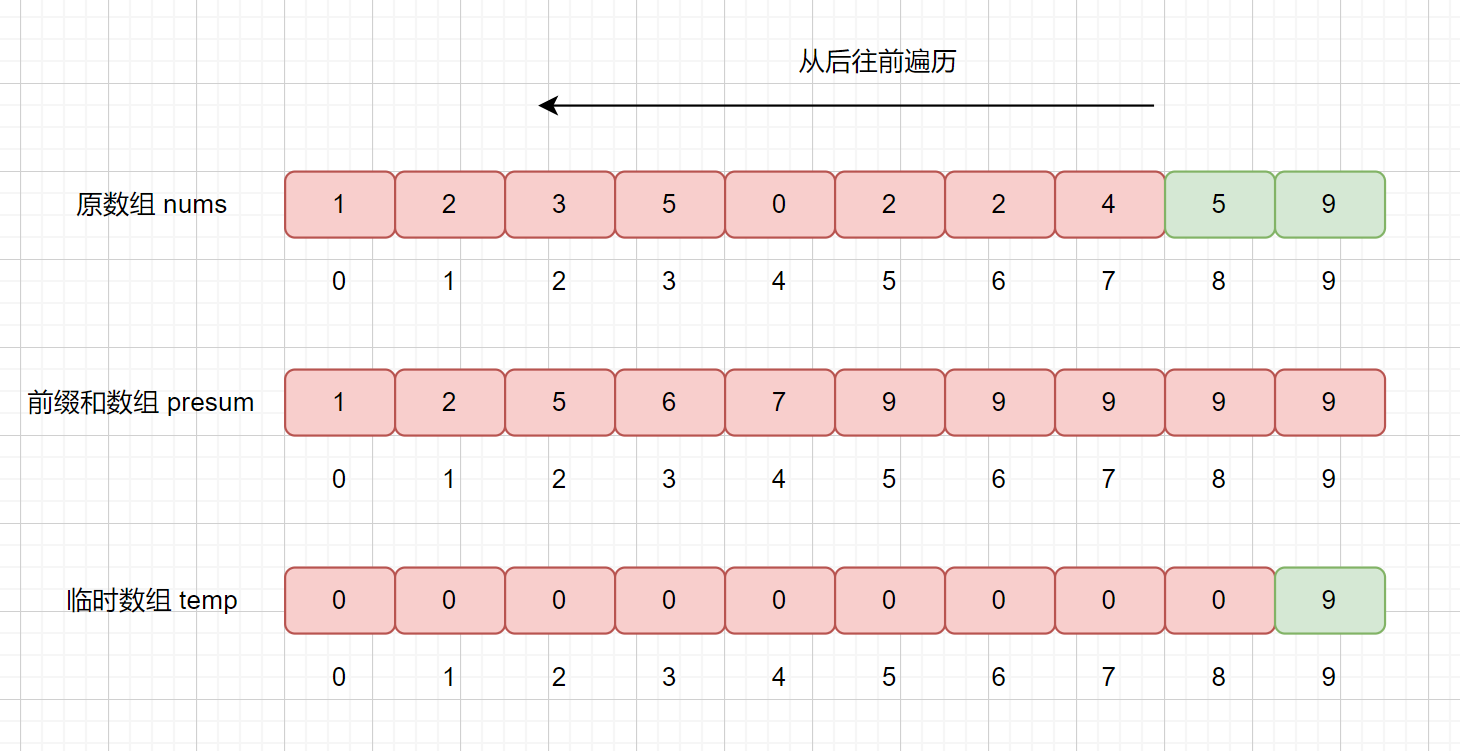
我們繼續查詢 presum 數組，發現 presum[5] = 9,則說明小于等于 5 的數共有 9 個，我們將其放入到 temp 數組的第 9 個位置，也就是

temp[8] = 5。然后再將 presum[5] 減 1 。

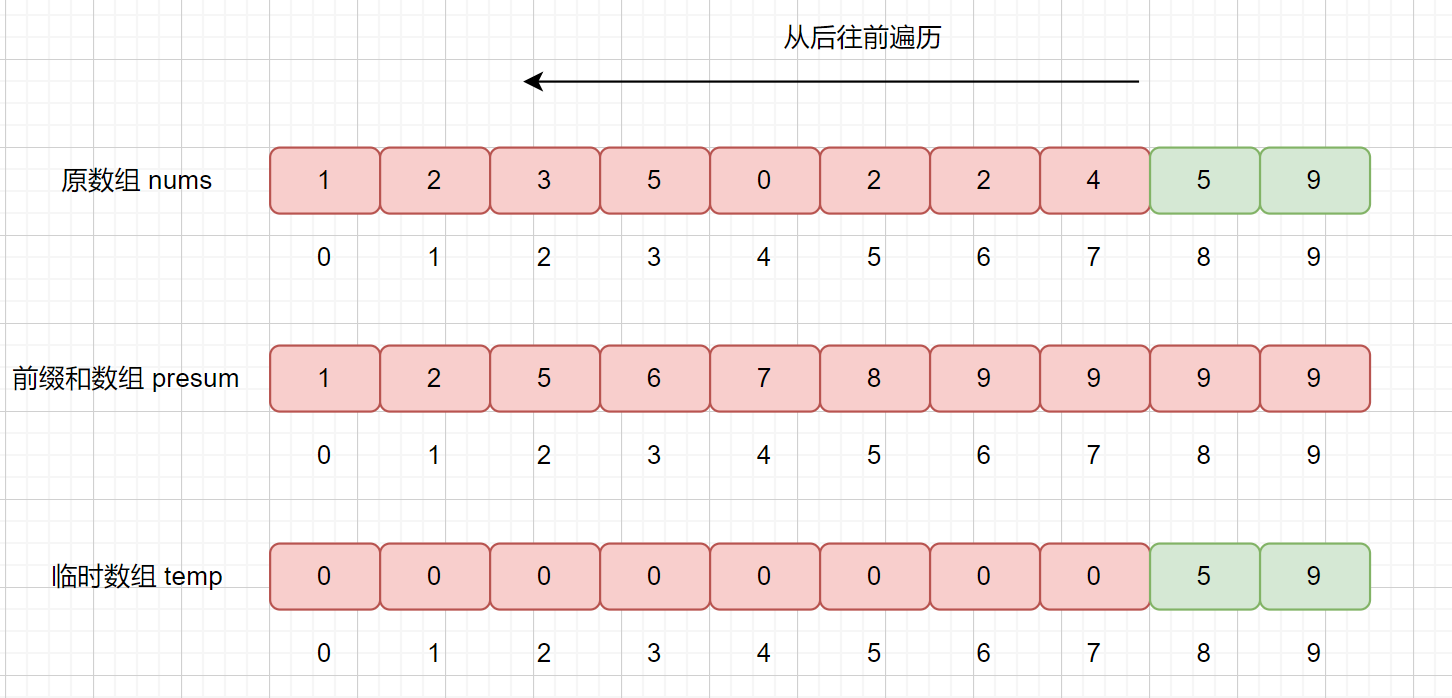
是不是到這里就理解了計數排序的大致思路啦。

這個排序的過程像不像查字典呢？通過查詢 presum 數組，得出自己應該排在臨時數組的第幾位。然后再修改下字典，直到遍歷結束。

那么我們先來用動畫模擬一下我們這個 bug 版的計數排序，加深理解。

注：我們得到 presum 數組的過程在動畫中省略。直接模擬排序過程。

但是到現在就完了嗎？顯然沒有，我們思考下這個情況。

假如我們的數字為 90，93，94，91，92 如果我們根據上面方法設置 presum 數組的長度，那我們則需要設置數組長度為 95（因為最大值是94），這樣顯然是不合理的，會浪費掉很多空間。

還有就是當我們需要對負數進行排序時同樣會出現問題，因為我們求次數的時候是根據 nums[index] 的值來填充 presum 數組的，所以當 nums[index] 為負數時，填充 presum 數組時則會報錯。而且此時通過最大值來定義數組長度也不合理。

所以我們需要采取別的方法來定義數組長度。

下面我們來說一下偏移量的概念。

例如 90，93，94，91，92，我們 可以通過 max ，min 的值來設置數組長度即 94 - 90 + 1 = 5 。偏移量則為 min 值，也就是 90。

見下圖。

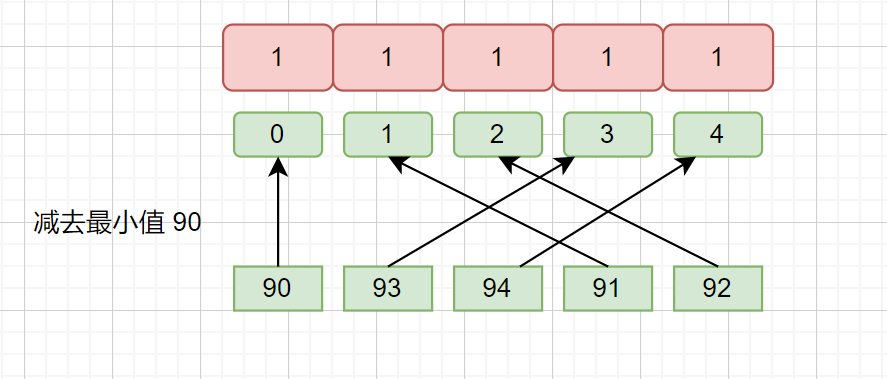
這樣我們填充 presum 數組時就不會出現浪費空間的情況了，負數？出現負數的情況當然也可以。繼續看

例如：-1，-3，0，2，1

一樣可以，哦了，到這里我們就搞定了計數排序，下面我們來看一哈代碼吧。

class Solution {public int[] sortArray(int[] nums) {int len = nums.length;if (nums.length < 1) {return nums;}//求出最大最小值int max = nums[0];int min = nums[0];for (int x : nums) {if (max < x)  max = x;       if (min > x)  min = x;         }//設置 presum 數組長度,然后求出我們的前綴和數組，//這里我們可以把求次數數組和前綴和數組用一個數組處理int[] presum = new int[max-min+1];for (int x : nums) {presum[x-min]++;}for (int i = 1; i < presum.length; ++i) {presum[i] = presum[i-1]+presum[i]; }//臨時數組int[] temp = new int[len];//遍歷數組，開始排序,注意偏移量for (int i = len-1; i >= 0; --i) {//查找 presum 字典，然后將其放到臨時數組，注意偏移度int index = presum[nums[i]-min]-1;temp[index] = nums[i];//相應位置減一presum[nums[i]-min]--;           }//copy回原數組System.arraycopy(temp,0,nums,0,len);return nums;}
}

好啦，這個排序算法我們已經搞定了，下面我們來扒一扒它。

計數排序時間復雜度分析

我們的總體運算量為 n+n+k+n ，總體運算是 3n + k 所以時間復雜度為 O(N+K)；

計數排序空間復雜度分析

我們用到了輔助數組，空間復雜度為 O（n）

計數排序穩定性分析

穩定性在我們最后存入臨時數組時有體現，我們當時讓其放入臨時數組的合適位置，并減一，所以某元素前面的相同元素，在臨時數組，仍然在其前面。所以計數排序是穩定的排序算法。

雖然計數排序效率不錯但是用到的并不多。

• 這是因為其當數組元素的范圍太大時，并不適合計數排序，不僅浪費時間，效率還會大大降低。

• 當待排序的元素非整數時,也不適用,大家思考一下這是為什么呢?

好啦,今天的文章就到這啦,我們下期再見,拜了個拜.

另外關于可以用排序算法秒殺的題目，后面會給大家更新上來，如果現在需要的話，可以去我的倉庫。

倉庫地址：GitHub - chefyuan/algorithm-base: 一位酷愛做飯的程序員，立志用動畫將算法說的通俗易懂。我的面試網站 www.chengxuchu.com

里面還有其他很多動畫題解，歡迎各位閱讀。