為什么你應該使用邏輯回歸來建模非線性決策邊界(使用 Python 代碼)
作為一名大數據從業者,復雜的機器學習技術非常具有吸引力。使用一些深度神經網絡 (DNN) 獲得額外的 1% 準確率,并在此過程中啟動 GPU 實例,這讓人非常滿意。然而,這些技術通常將思考留給計算機,讓我們對模型的工作原理了解甚少。所以,我想回到基礎知識。
在本文中,我希望教你一些關于特征工程的知識,以及如何使用它來建模非線性決策邊界。我們將探討兩種技術的優缺點:邏輯回歸(帶有特征工程)和 NN 分類器。將提供用于擬合這些模型以及可視化其決策邊界的 Python 代碼。你可以在 Github1 上找到完整的項目代碼。最后,我希望讓你理解為什么特征工程可能是其他非線性建模技術的更好替代方案。
什么是特征工程
當你從原始數據創建特征或將現有特征的函數添加到數據集時,你就在進行特征工程。這通常使用特定領域的領域知識來完成2。例如,假設我們想要預測一個人從手術中恢復所需的時間(Y)。從之前的手術中,我們獲得了患者的康復時間、身高和體重。根據這些數據,我們還可以計算出每個患者的 BMI = 身高/體重2。通過計算 BMI 并將其納入數據集,我們正在進行特征工程。
我們為什么要進行特征工程
特征工程非常強大,因為它允許我們將非線性問題重新表述為線性問題。為了說明這一點,假設恢復時間與身高和體重有以下關系:
Y = β 0 + β 1 (高度) + β 2 (重量) + β 3 (高度 / 重 量 2 ) + 噪聲 Y = \beta_0 + \beta_1(高度)+ \beta_2(重量)+ \beta_3(高度/重量^2)+ 噪聲 Y=β0?+β1?(高度)+β2?(重量)+β3?(高度/重量2)+噪聲
查看第 3 項,我們可以看到 Y 與身高和體重沒有線性關系。這意味著我們可能不會期望線性模型(例如線性回歸)能夠很好地估計 β 系數。你可以嘗試使用非線性模型(例如 DNN),或者我們可以通過進行一些特征工程來幫助我們的模型。如果我們決定將 BMI 作為一個特征,則關系將變為:
Y = β 0 + β 1 (高度) + β 2 (重量) + β 3 ( B M I ) + 噪聲 Y = \beta_0 + \beta_1(高度)+ \beta_2(重量)+ \beta_3(BMI)+ 噪聲 Y=β0?+β1?(高度)+β2?(重量)+β3?(BMI)+噪聲
Y 現在可以被建模為 3 個變量的線性關系。因此,我們期望線性回歸能夠更好地估計系數。稍后,我們將看到同樣的想法也適用于分類問題。
為什么不讓電腦來做這項工作
如果從技術角度來講,特征工程本質上就是核心技巧,因為我們將特征映射到更高的平面3。盡管使用核技巧通常不需要太多思考。核函數被視為超參數,可以使用蠻力找到最佳函數——嘗試大量不同的函數變體。使用正確的核函數,你可以建模非線性關系。給定正確數量的隱藏層 / 節點,DNN 還將自動構建特征的非線性函數2。那么,如果這些方法可以建模非線性關系,我們為什么還要費心進行特征工程呢?
我們上面解釋了特征工程如何讓我們即使在使用線性模型的情況下也能捕捉數據中的非線性關系。這意味著,根據問題的不同,我們可以實現與非線性模型類似的性能。我們將在本文后面詳細介紹一個示例。除此之外,使用特征工程還有其他好處,這使得這項技術很有價值。

首先,你會更好地理解模型的工作原理。這是因為你確切地知道模型使用什么信息進行預測。此外,像邏輯回歸這樣的模型可以通過直接查看特征系數來輕松解釋。第二個原因與第一個原因相符,即模型更容易解釋。如果你在工業界工作,這一點尤其重要。你的同事也更有可能接觸到一些更簡單的模型。第三個原因是你的模型不太可能過度擬合訓練數據。通過強制加載不同的超參數,很容易導致對數據中噪聲建模。相比之下,有了深思熟慮的特征,你的模型將是直觀的,并且很可能模擬真實的潛在趨勢。
數據集
讓我們深入研究一個實際的例子。為了盡可能清晰,我們將使用人工生成的數據集。為了避免這個例子太枯燥,我們將圍繞它創建一個敘述。假設你的人力資源部門要求你創建一個模型來預測員工是否會晉升。該模型應該考慮員工的年齡和績效分數。
我們在下面的代碼中為 2000 名假設員工創建特征。員工的年齡可以在 18 到 60 歲之間。績效分數可以在 -10 到 10 之間(10 為最高)。這兩個特征都經過了打亂,因此它們不相關。然后我們使用以下年齡 (a) 和績效 § 函數來生成目標變量:
γ ( a , p ) = 100 ( a ) + 200 ( p ) + 500 ( a / p ) ? 10000 + 500 ( n o i s e ) \gamma(a,p)= 100(a)+ 200(p)+ 500(a / p)- 10000 + 500(noise) γ(a,p)=100(a)+200(p)+500(a/p)?10000+500(noise)
當 γ ( a , p ) ≥ 0 \gamma(a,p)≥ 0 γ(a,p)≥0 時,員工會得到晉升;當 $\gamma(a,p) < 0 $?時,員工不會得到晉升。我們可以看到,上面的函數中包含了 a/p 項。這意味著決策邊界將不是年齡和績效的線性函數。還包括隨機噪聲,因此數據不是完全可分離的。換句話說,模型不可能 100% 準確。
import numpy as np
import pandas as pdn_points = 2000age = np.round(np.linspace(18, 60, n_points), 2) # age of employee
np.random.shuffle(age) # shuffleperformance = np.linspace(-10, 10, n_points) # performance score of employee
np.random.shuffle(performance) # shufflenoise = np.random.randn(n_points)g = (100 * age) + 200 * (performance) + 500 * age / performance - 10000 + 500 * noise
y = [1 if y >= 0 else 0 for y in g]data = pd.DataFrame(data = {'age': age, 'performance': performance, 'y': y})print(sum(y))
data.head()---
474age performance y
0 53.32 -6.098049 0
1 32.10 -7.848924 0
2 58.72 9.709855 1
3 59.52 4.387194 1
4 28.55 7.418709 0
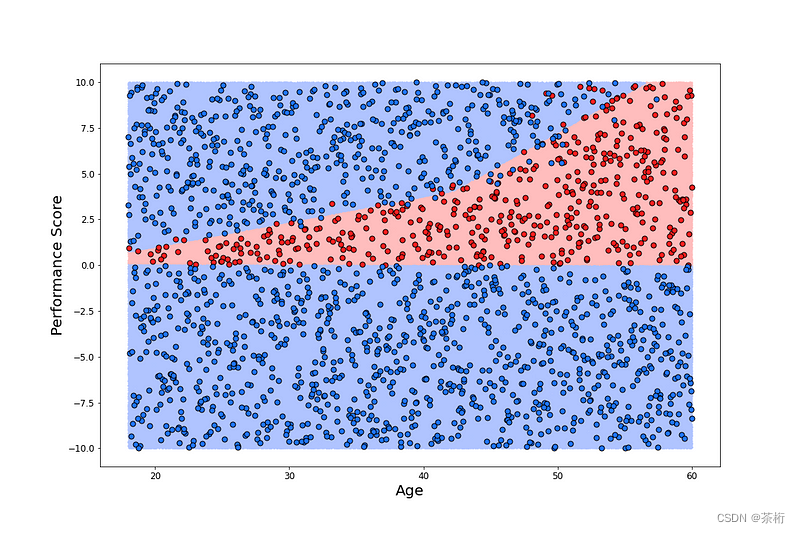
如果上述步驟有點令人困惑,請不要擔心。我們可以通過使用以下代碼可視化數據集來使事情變得更清晰。在這里,我們創建了數據的散點圖,結果可以在圖 1 中看到。僅通過兩個特征,很容易準確地看到發生了什么。在 y 軸上,我們有員工的績效分數,在 x 軸上,我們有員工的年齡。晉升員工的分數為紅色,未晉升的員工分數為藍色。最終,2000 名員工中有 459 名(23%)獲得了晉升。對于不同的隨機樣本,該比例會略有變化。
plt.subplots(nrows = 1, ncols = 1, figsize = (15, 10))plt.scatter('age', 'performance', c = '#ff2121', s = 50, edgecolors = '#000000', data = data[data.y == 1])
plt.scatter('age', 'performance', c = '#2176ff', s = 50, edgecolors = '#000000', data = data[data.y == 0])
plt.ylabel('Performance Score', size = 20)
plt.xlabel('Age', size = 20)
plt.yticks(size = 12)
plt.xticks(size = 12)
plt.legend(['Promoted', 'Not Promoted'], loc = 2, prop = {'size': 20})
plt.savefig('../figures/article_feature_eng/figure1.png', format = 'png')
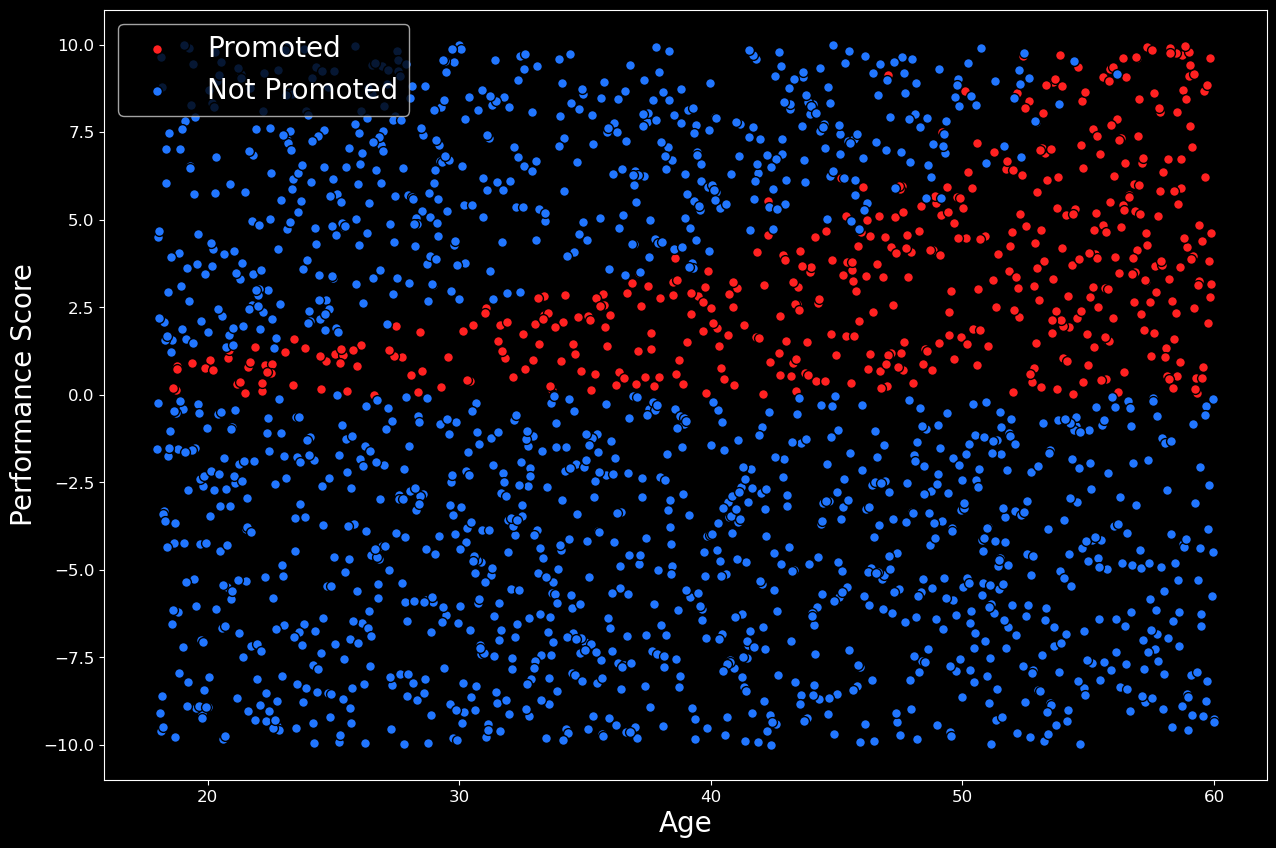
盡管這些數據是生成的,但我們仍然可以對該圖做出現實的解釋。在圖 1 中,我們可以看到 3 個不同的員工組。第一個是績效得分低于 0 的組。由于績效不佳,這些員工中的大多數都沒有得到晉升,我們還可以預期其中一些員工被解雇。我們可以預期得分高于 0 的員工要么得到晉升,要么接受其他公司的報價。得分特別高的員工往往會離開。這可能是因為他們的需求量很大,而且在其他地方得到了更好的報價。然而,隨著雇主年齡的增長,他們需要更高的績效分數才能離開。這可能是因為年長的員工在目前的職位上更舒服。
無論如何,很明顯,決策邊界不是線性的。換句話說,不可能畫出一條直線來很好地區分晉升組和未晉升組。因此,我們不會指望線性模型能做得很好。讓我們通過嘗試僅使用兩個特征(年齡和表現)來擬合邏輯回歸模型來證明這一點。
邏輯回歸
在下面的代碼中,我們將 2000 名員工分成訓練集(70%)和測試集(30%)。我們使用訓練集來訓練邏輯回歸模型。然后,使用該模型,我們對測試集進行預測。測試集的準確率為 82%。這似乎不算太糟糕,但我們應該考慮到只有不到 23% 的員工獲得了晉升。因此,如果我們只是猜測沒有員工會得到晉升,那么我們應該預期準確率約為 77%。
from sklearn.model_selection import train_test_split
import sklearn.metrics as metric
import statsmodels.api as smx = data[['age', 'performance']]
x = sm.add_constant(x)
y = data['y']
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.3, random_state = 2024)model = sm.Logit(y_train, x_train).fit() # fit logistic regression modelpredictions = np.around(model.predict(x_test))
accuracy = metric.accuracy_score(y_test, predictions)print(round(accuracy * 100, 2))---
Optimization terminated successfully.Current function value: 0.428402Iterations 7
81.83
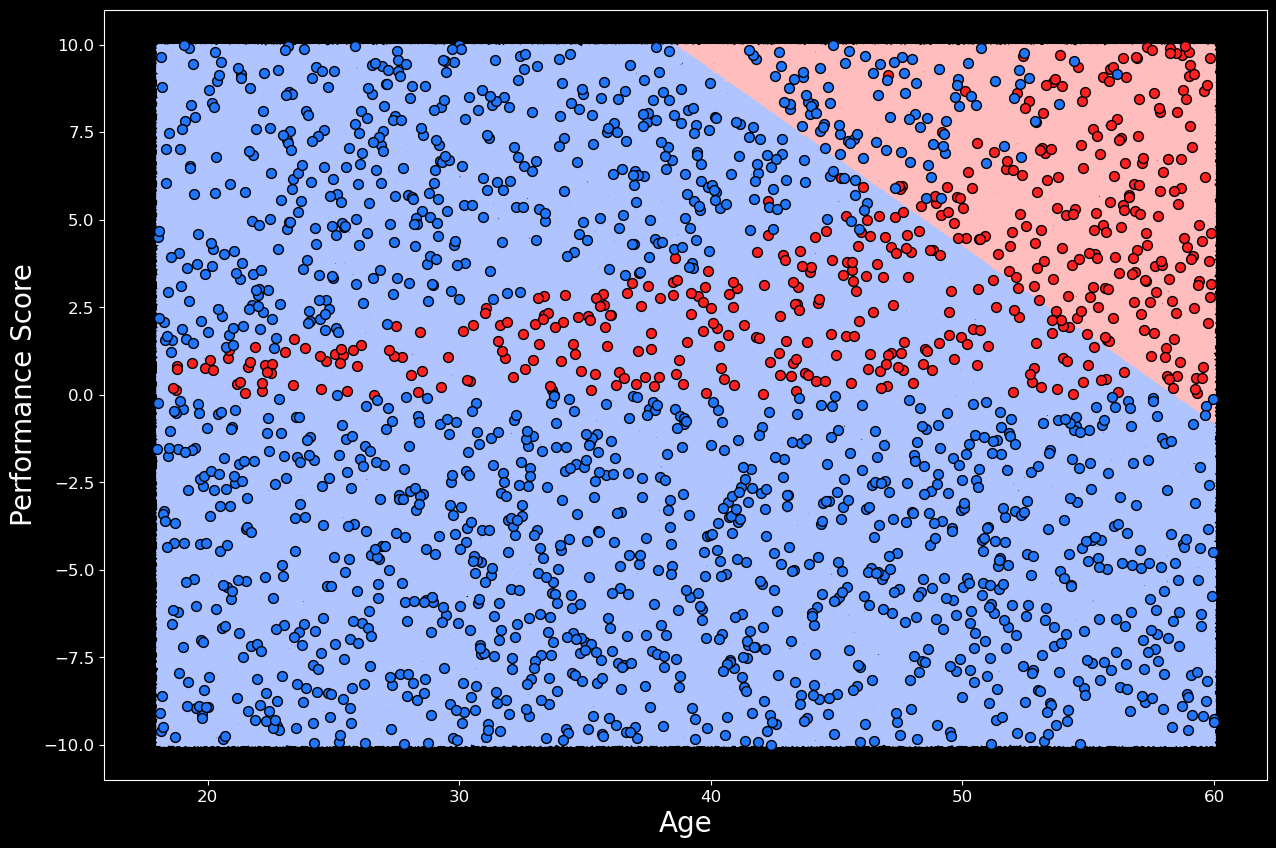
通過使用以下代碼可視化決策邊界,我們可以更好地理解模型正在做什么。在這里,我們在樣本空間內生成一百萬個點。然后,我們使用邏輯回歸模型對所有這些點進行預測。與圖 1 中的散點圖一樣,我們可以繪制每個點。每個點的顏色由模型的預測決定 — 如果模型預測晉升,則為粉紅色,否則為淺藍色。這為我們提供了決策邊界的良好近似值,可以在圖 2 中看到。然后,我們可以在這些點上繪制實際數據集。
n_points = 1000000 # use many point to visualise decision boundryage_db = np.linspace(18, 60, n_points)
np.random.shuffle(age_db)performance_db = np.linspace(-10, 10, n_points)
np.random.shuffle(performance_db)data_db = pd.DataFrame({'age': age_db, 'performance': performance_db})
data_db = sm.add_constant(data_db)# make predictions on the decision boundry points
predictions = model.predict(data_db)
y_db = [round(p) for p in predictions]
data_db['y'] = y_dbfig, ax = plt.subplots(nrows = 1, ncols = 1, figsize = (15, 10))# Plot decision boundry
plt.scatter('age', 'performance', c = '#ffbdbd', s = 1, data = data_db[data_db.y == 1])
plt.scatter('age', 'performance', c = '#b0c4ff', s = 1, data = data_db[data_db.y == 0])# Plot employee data points
plt.scatter('age', 'performance', c = '#ff2121', s = 50, edgecolors = '#000000', data = data[data.y == 1])
plt.scatter('age', 'performance', c = '#2176ff', s = 50, edgecolors = '#000000', data = data[data.y == 0])
plt.ylabel('Performance Score', size = 20)
plt.xlabel('Age', size = 20)
plt.yticks(size = 12)
plt.xticks(size = 12)plt.savefig('../figures/article_feature_eng/figure2.png', format = 'png')
從決策邊界來看,我們可以看到模型表現很糟糕。它預測會升職的員工中,大約有一半沒有升職。然后,對于大多數獲得晉升的員工,它預測他們沒有獲得晉升。請注意,決策邊界是一條直線。這強調了邏輯回歸是一個線性分類器。換句話說,該模型只能構建一個決策邊界,它是你賦予它的特征的線性函數。此時,我們可能會想嘗試不同的模型,但讓我們看看是否可以使用特征工程來提高性能。
具有特征工程的邏輯回歸
首先,如下面的代碼所示,我們添加了附加特征(即年齡與表現的比率)。從那時起,我們遵循與之前的模型相同的過程。訓練測試分割是相同的,因為我們對 “random_state” 使用相同的值。最后,這個模型的準確率達到了 98%,這是一個顯著的改進。
data['age_perf_ratio'] = age / performancex = data[['age', 'performance', 'age_perf_ratio']]
x = sm.add_constant(x)
y = data['y']x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.3, random_state = 2024)model = sm.Logit(y_train, x_train).fit() # fit new logistic regression modelpredictions = np.around(model.predict(x_test))
accuracy = metric.accuracy_score(y_test, predictions)print(round(accuracy * 100, 2))---
Optimization terminated successfully.Current function value: 0.039001Iterations 17
98.17
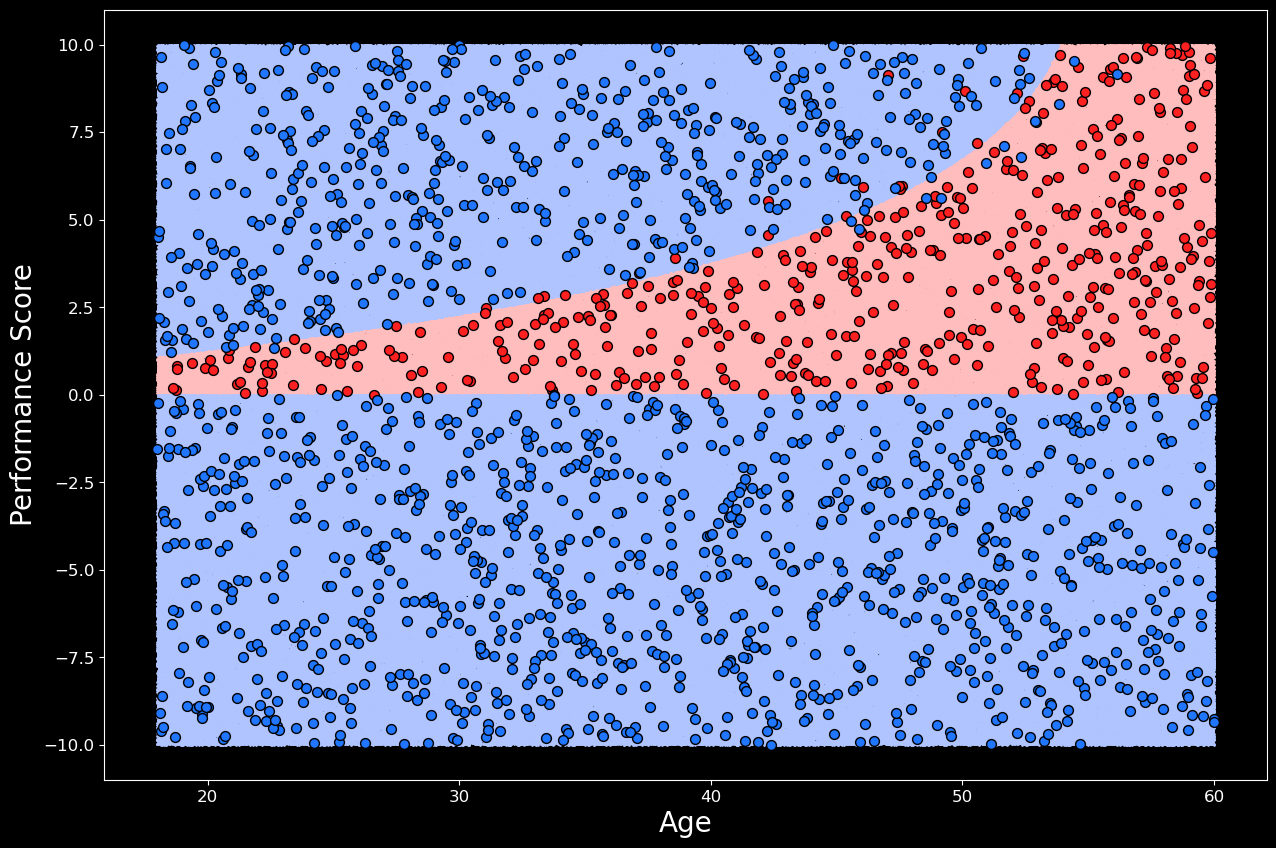
該模型仍然只需要員工的年齡和績效即可進行預測。這是因為附加特征是年齡和績效的函數。這使我們能夠以與以前相同的方式可視化決策邊界。即通過在樣本空間中的每個年齡-績效點使用模型的預測。我們可以看到,在圖 3 中,通過添加附加特征,邏輯回歸模型能夠對非線性決策邊界進行建模。從技術上講,這是年齡和績效的非線性函數,但它仍然是所有 3 個特征的線性函數。
使用邏輯回歸的另一個好處是模型是可解釋的。這意味著模型可以用人類的術語來解釋4。換句話說,我們可以直接查看模型系數來了解其工作原理。我們可以在表 1 中看到模型特征的系數及其 p 值。我們不會講得太詳細,但系數可以讓你根據晉升幾率的變化來解釋特征的變化5。如果特征具有正系數,則該特征值的增加會導致晉升幾率的增加。
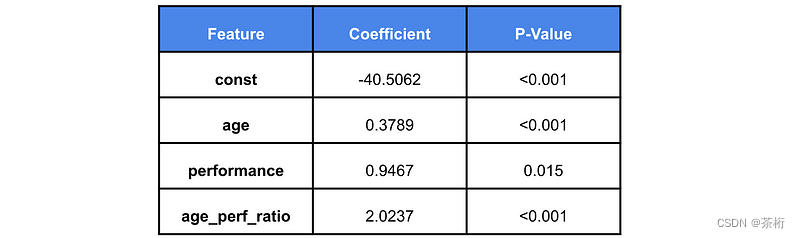
從表 1 可以看出,隨著年齡的增長,獲得晉升的可能性也會增加。另一方面,對于績效,這種關系并不那么明顯。績效的提高也會降低年齡/績效比率。這意味著,績效提高對幾率的影響取決于員工的年齡。這非常符合直覺,因為它與我們在散點圖中看到的一致。在這種情況下,可能沒有必要使用系數以這種方式解釋模型。僅僅可視化決策邊界就足夠了,但是,隨著我們增加特征數量,這樣做變得更加困難。在這種情況下,模型系數是理解模型如何工作的重要工具。
同樣,P 值也有助于我們對模型的理解。由于系數是統計估計值,因此具有一定的不確定性。換句話說,我們可以確定系數要么是正值,要么是負值。這一點非常重要,因為如果我們不能確定系數的符號,就很難用幾率的變化來解釋特征的變化。從表 1 中我們可以看出,所有系數在統計意義上都是顯著的。這并不奇怪,因為我們是利用特征函數生成數據的。
總體而言,當我們生成數據時,上述分析非常簡單。因為我們知道使用什么函數來生成數據,所以很明顯,附加特征會提高模型的準確性。實際上,事情不會這么簡單。如果你對數據沒有很好的理解,你可能需要與人力資源部門的某個人交談。他們可能會告訴你他們過去看到的任何趨勢。否則,通過使用各種圖表和匯總統計數據探索該數據,你可以了解哪些特征可能很重要。但是,假設我們不想做所有這些艱苦的工作。
神經網絡
為了進行比較,我們使用非線性模型。在下面的代碼中,我們使用 Keras 來擬合 NN。我們僅使用年齡和表現作為特征,因此 NN 的輸入層的維度為 2。有 2 個隱藏層,分別有 20 個和 15 個節點。兩個隱藏層都具有 relu 激活函數,輸出層具有 sigmoid 激活函數。為了訓練模型,我們使用 10 和 100 個 epoch 的批處理大小。訓練集大小為 1400,這給了我們 14000 個步驟。最后,該模型在測試集上的準確率達到了 96%。這與邏輯回歸模型的準確率略低,但是也相差不大,不過我們不必進行任何特征工程。
from keras.models import Sequential
from keras.layers import Densex = data[['age', 'performance']]
y = data['y']
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.3, random_state = 2024)model = Sequential()model.add(Dense(20, input_dim = 2, activation = 'relu'))
model.add(Dense(15, activation = 'relu'))
model.add(Dense(1, activation = 'sigmoid'))
model.compile(loss = 'binary_crossentropy', optimizer = 'adam', metrics = ['accuracy'])model.fit(x_train, y_train, epochs = 100, batch_size = 10) # fit ANNaccuracy = model.evaluate(x_test, y_test)
print(round(accuracy[1] * 100, 2))---
Epoch 1/100
2024-06-30 22:31:06.692852: W tensorflow/core/platform/profile_utils/cpu_utils.cc:128] Failed to get CPU frequency: 0 Hz
2024-06-30 22:31:06.891137: I tensorflow/core/grappler/optimizers/custom_graph_optimizer_registry.cc:113] Plugin optimizer for device_type GPU is enabled.
140/140 [==============================] - 3s 4ms/step - loss: 0.5638 - accuracy: 0.7393
...
Epoch 100/100
140/140 [==============================] - 1s 6ms/step - loss: 0.0943 - accuracy: 0.9543
Output is truncated. View as a scrollable element or open in a text editor. Adjust cell output settings...
2024-06-30 22:32:14.638250: I tensorflow/core/grappler/optimizers/custom_graph_optimizer_registry.cc:113] Plugin optimizer for device_type GPU is enabled.
19/19 [==============================] - 1s 10ms/step - loss: 0.0848 - accuracy: 0.9617
96.17
通過查看圖 4 中的 NN 決策邊界,我們可以看出為什么它被認為是一種非線性分類算法。即使我們只給出了模型年齡和性能,它仍然能夠構建非線性決策邊界。因此,在一定程度上,模型已經為我們完成了艱苦的工作。你可以說模型的隱藏層已經自動完成了特征工程。那么,考慮到這個模型具有很高的準確性并且需要我們付出的努力較少,我們為什么還要考慮邏輯回歸呢?
NN 的缺點是它只能解釋。這意味著,與邏輯回歸不同,我們不能直接查看模型的參數來了解其工作原理4。我們可以使用其他方法,但最終,理解 NN 的工作原理更加困難。向非技術人員(例如人力資源主管)解釋這一點更加困難。這使得邏輯回歸模型在行業環境中更有價值。
工業界和學術界都存在許多問題,其中大多數問題都比本文給出的示例更復雜。本文提出的方法顯然不是解決所有這些問題的最佳方法。例如,如果你嘗試進行圖像識別,那么使用邏輯回歸將無濟于事。對于較簡單的問題,邏輯回歸和對數據的良好理解通常就是你所需要的。
參考
茶桁的公共文章項目庫(2024 年),https://github.com/hivandu/public_articles ??
T. Hastie, R. Tibshirani, J. Friedman, The Elements of Statistical Learning [pg 150] (2017), https://web.stanford.edu/~hastie/ElemStatLearn/ ?? ??
Statinfer, The Non-Linear Decision Boundary (2017), https://statinfer.com/203-6-5-the-non-linear-decision-boundary/ ??
R. Gall, Machine Learning Explainability vs Interpretability: Two concepts that could help restore trust in AI (2018), https://www.kdnuggets.com/2018/12/machine-learning-explainability-interpretability-ai.html ?? ??
UCLA, How do I Interpret Odds Ratios in Logistic Regression? (2020), https://stats.idre.ucla.edu/stata/faq/how-do-i-interpret-odds-ratios-in-logistic-regression/ ??

















)
Adobe Flash Player已不再受支持)
