#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <assert.h>
#define MAX 100
#define NO INT_MAX//NO表示沒有邊,相當于INFtypedef struct Graph
{int arcnum;int vexnum;char vextex[MAX][20];int martrix[MAX][MAX];
}Graph;
//鄰接矩陣打印輸出圖
void print_graph(Graph* g)
{for (int i = 0; i < g->vexnum; i++){printf("\t%s", g->vextex[i]);}printf("\n");for (int i = 0; i < g->vexnum; i++){printf("%s\t", g->vextex[i]);for (int j = 0; j < g->vexnum; j++){if (g->martrix[i][j] == INT_MAX){printf("∞\t");}else{printf("%d\t", g->martrix[i][j]);}}printf("\n");}
}
//定義最小生成樹的邊結構
typedef struct Arc
{int begin;int end;int weight;//在邊結構中加多了一個權值weight來用于判斷構造最小生成樹
}Arc;
//打印最小生成樹
void print_tree(Graph* g, Arc* arc, int count)
{printf("最小生成樹:\n");for (int i = 0; i < count; i++){printf("%s--->%s\n", g->vextex[arc[i].begin], g->vextex[arc[i].end]);}
}
//比較函數(用于在qsort中,因為qsort是一個泛函數,開始時未知函數類型,需要在調用函數時再給出),
//所以這個比較基準函數需要使用強制類型轉換
int compare_arc(const void* a, const void* b)
{return(((Arc*)a)->weight-((Arc*)b)->weight);//強制轉化為arc類型,根據邊結構的weight值進行比較,如果大于則返回正數,等于則返回0,小于則返回負數
}
//克魯斯卡爾算法
void graph_kruskal(Graph* g)
{//定義邊結構數組arc用于保存圖中存在的邊Arc* arc = (Arc*)malloc(sizeof(Arc) * g->vexnum * g->vexnum);assert(arc);int count=0;//count用于存邊for (int i = 0; i < g->vexnum; i++){for (int j = 0; j < g->vexnum; j++){if (g->martrix[i][j] != NO){(arc + count)->begin = i;(arc + count)->end = j;(arc + count)->weight = g->martrix[i][j];count++;}}}//快速排序根據邊權值進行排序//(注意快速排序是不穩定的,所以選邊的順序不是按照原順序的)qsort(arc,count,sizeof(Arc),compare_arc);//定義parent整型數組,大小為頂點數int* parent = (int*)malloc(sizeof(int) * g->vexnum);assert(parent);for (int i = 0; i < g->vexnum; i++){parent[i] = i;//初始化時先將每個結點的前驅結點都置為自身}Arc* result = (Arc*)malloc(sizeof(Arc) * g->arcnum);//result是用于存儲對邊進行排序后的邊結構 assert(result);count = 0;//count用于跟蹤已選的邊的數量int i = 0;//i用于遍歷所有的邊printf("Kruskal的選邊過程如下:\n");while (count < g->vexnum - 1)//當邊沒選夠時則繼續進行{int x = (arc + i)->begin;int y = (arc + i)->end;//初始化兩個變量來存x和y的根節點int root_x = x;int root_y = y;while (parent[root_x] != root_x){root_x = parent[root_x];//進行壓縮路徑,將其根節點設為根節點的根節點}while (parent[root_y] != root_y){root_y = parent[root_y];}if (root_x != root_y)//如果不構成一個環的話{result[count] = arc[i]; //將該邊加入到最小生成樹中count++;printf("選擇邊:%s---%s,權值為:%d\n",g->vextex[x],g->vextex[y],g->martrix[x][y]);parent[root_x] = root_y;//將所選邊前面點的前驅節點置為后邊的點(也是起到類似壓縮路徑的效果,誰先誰后好像關系不大)}i++;}print_tree(g, arc, count);free(arc);free(result);free(parent);
}int main()
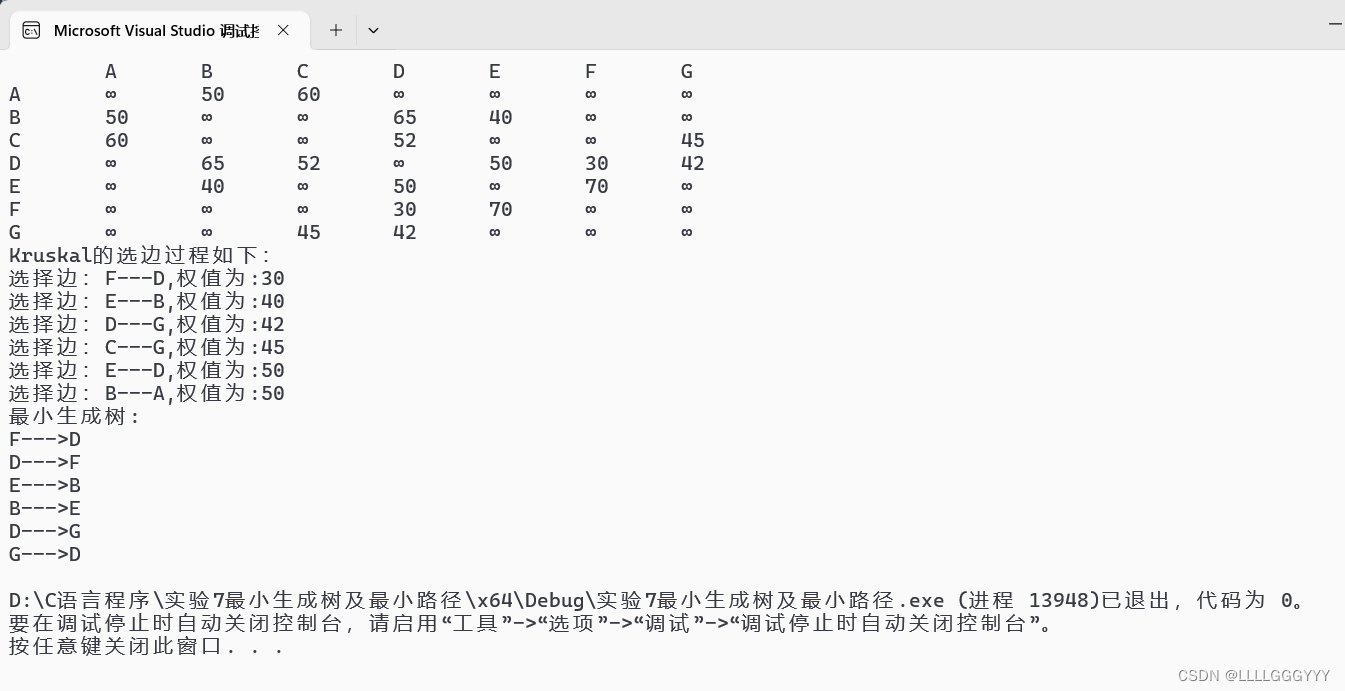
{Graph g = { 10,7,{"A","B","C","D","E","F","G"},{{NO,50,60,NO,NO,NO,NO},{50,NO,NO,65,40,NO,NO},{60,NO,NO,52,NO,NO,45},{NO,65,52,NO,50,30,42},{NO,40,NO,50,NO,70,NO},{NO,NO,NO,30,70,NO,NO},{NO,NO,45,42,NO,NO,NO}} };print_graph(&g);graph_kruskal(&g);return 0;
}




)





)






用與數據整合和批次處理)


